含水率对结构性参数影响的单变量模型

程大伟，骆亚生，陈茜，郭鸿

(西北农林科技大学 水利与建筑工程学院，陕西 杨凌，712100)

摘要：基于侧限压缩试验分析不同压力条件下原状样和重塑样的割线模量随含水率变化规律，获取割线模量与含水率关系的表达式。基于应变的结构性参数可化简为以割线模量为参量的结构性参数，并将割线模量与含水率关系式代入即可构建含水率对结构性参数影响的单变量模型。最后检验含水率对结构性参数影响的单变量模型。研究结果表明：不同压力条件下原状样和重塑样的割线模量均随含水率增大而呈递减趋势，但由于原状样存在明显的结构强度，不同压力下原状样割线模量与含水率关系曲线存在交叉；采用含水率作为单变量描述的结构性参数能够直观地反映土体结构性随含水率的变化规律；不同压力条件下结构性参数随含水率的增大呈递减趋势，但随着压力条件的不同，这种递减趋势存在差异。当压力较小时，结构性参数随含水率递减的趋势较平缓；当压力较大时，结构性参数随含水率递减的趋势是快速递减；在这两者之间则呈现出先平缓递减后快速递减的过渡状态。

关键词：结构性；割线模量；含水率；单变量模型；侧限压缩试验

中图分类号：TU435          文献标志码：A         文章编号：1672-7207(2014)06-2047-07

Single variable model of water contents on structural parameter impact

CHENG Dawei, LUO Yasheng, CHEN Xi, GUO Hong

(College of Water Resources and Architectural Engineering, Northwest A& F University, Yangling, 712100, China)

Abstract: Based on confined compression test, the change law of secant modulus and water contents was analyzed with undisturbed and disturbed sample under different pressure conditions, and the expression was obtained. Structural parameters based on the same strain method can be simplified to the structural parameter expression by secant modulus. The single variable model of water contents on structural parameter impact was established by substituting the expression of secant modulus and water contents. The single variable model was verified. The results show that secant modulus of undisturbed and disturbed sample decreases with the increase of the water contents under different pressure conditions. However, due to the obvious existing structural strength, undisturbed sample displays obvious structural strength, and undisturbed sample secant modulus keeps the same value for some different water contents. Structural parameter, which regards water content as the single variable, is able to reflect the change law of soil structure and water content. Under different pressure conditions, structural parameter decreases with the increase of the water contents. But the law of structural parameter and water contents is different with pressure conditions. Under low pressure conditions, structural parameters decrease slowly. Under high pressure conditions, structural parameters decrease significantly. Between these two conditions, structural parameters decrease slightly at first and then decrease dramatically.

Key words: structural; secant modulus; water contents; single variable model; confined compression test

土的结构性是土物理状态的反映^[1]，也是决定土的力学性质的一个根本内在因素。Terzaghi^[2]首先研究了结构性对土力学性质的影响，Skempton等^[3-5]通过试验对此进行了验证。土的结构性是指构成土体的颗粒的形状、大小、表面特征、定量的比例关系、空间上的排列状态、骨架颗粒与胶结物的胶结形式，以及孔隙的形态、大小、数量和分布情况^[6]，在力学性质上表现为土体保存原结构状态不被破坏的能力^[7-8]。土的结构性是全面反映土颗粒排列(几何特征)和土颗粒连接特征(力学特征)的综合特征。土的结构性对土工程性质有重要影响^[9]。在土结构性研究的3大基本途径^[1]中，土力学的研究方法因其具有简单、明确、可靠、易测等优点^[10]引起学者们的广泛关注。齐吉琳等^{[6, 11]}提出的基于释放土体结构势思想确定土体结构的定量化参数。自邵生俊等^[12-13]通过三轴试验，基于原状土、重塑土和饱和土的主应力差之比值构建了结构性参数，并将其引入原状黄土应力-应变关系分析中，建立了非饱和湿陷性黄土的本构模型；骆亚生等^[14-15]基于三轴试验提出了基于应力的结构性参数，建立了对应于复杂应力条件的土结构性本构模型。夏望民^[16]在总结黄土的变形强度特性、湿陷和增湿变形特性的基础上提出了一种用原状黄土、重塑饱和黄土割线模量表示的黄土结构性参数，该参数可以较好反映黄土在加载和增湿作用下结构变化和破损的过程。陈存礼等^[17-19]根据同一压力下原状、重塑及饱和黄土的孔隙比定义了一个定量结构性参数，探讨了结构性参数随压力及含水率变化的规律性。冯志焱^[20]提出了试锥下沉结构性参数，将释放结构性的思想与锥形稠度试验原理相结合，给出了测定原状土结构性参数作为土物理属性指标的方法。前人提出的结构参数其共同特点是以力的作用相关的变量(应变、应力、模量等)作为参量来描述结构性参数，而反映含水率对结构性参数影响的单变量模型构建专题研究鲜见报道。水和力作用是土结构性发生改变的两大主要因素^{[6, 21-23]}。在考察引起土结构发生变化的因素时，除应注意到力的作用以外，还应特别重视水的影响。土体中含水率的增大会使土中的化学胶结减弱、吸力减小，以及水的润滑作用等均会引起土结构的变化。因此，研究并揭示含水率的变化对土结构的影响规律亦具有重要意义。基于上述的分析，本文拟基于侧限压缩试验构建含水率对结构性参数影响的单变量模型，并对其进行检验、分析。

1  试验方法及数据

1.1  试验用土的基本性质

试验所用黄土土样为兰州黄土，取土深度为5 m，属于Q₃黄土。烘干法测得其天然含水率为5%，干密度为1.31 g/cm³，饱和含水率为35%。土样物理性质指标见表1。

表1  黄土土样的物理性质指标

Table 1  Physical indexes of Yangling loess

1.2  试验方法

在侧限压缩试验条件下测试基于应变考虑的结构性参数，其对试样的要求是每组试样采用1个原状样、1个对应相同干密度及含水率的重塑样和1个饱和原状样。试验设备为三联固结仪，分别对原状样和重塑样进行侧限压缩实验，土样含水率分别控制为5%，12%，19%，26%，33%和35%(根据结构性参数计算方法不需要进行饱和重塑样侧限压缩试验)，压力控制为50，100，200，300和400 kPa。试样面积为50 cm²，试样高为2 cm。原状黄土土样按天然含水率削制而成，重塑黄土土样按给定含水率压制而成，然后，采用风干法或采用滴水配水法将试样的含水率调节到试验要求值并养护3 d以上。饱和样直接在压缩仪上浸无气水饱和。

1.3  试验数据

分别整理并绘制不同含水率下兰州黄土原状样及重塑样的应变-应力关系曲线，如图1所示。

由图1可见：与重塑黄土的压缩曲线相比，原状样的压缩曲线具有明显的双拐点。其呈现的应变-应力关系的特点是在第一拐点前应变随应力近似呈线性增长，且斜率总体上较小；在第一拐点后应变斜率随应力的增长总体上变大，达到某一应力后出现第二拐点。此后，应变随应力的增长又趋于平缓。由图1(a)可见：兰州黄土原状样压缩曲线的第一拐点出现在0~100 kPa之间，随初始含水率的增大第一个拐点位置呈前移趋势。在初始含水率较低时，第二个拐点并不明显。文献[16]将第一拐点定义为类似于超固结土前期固结应力的黄土结构强度——黄土能够保持自身结构的最大应力。黄土的结构强度随含水率的增大而减小，接近饱和时趋向最小。而对于重塑黄土由于原有的结构已被破坏，可认为重塑黄土无明显结构强度，故重塑黄土的压缩曲线无明显的双拐点特征。

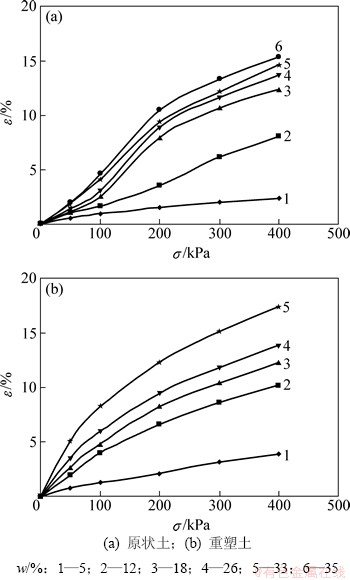
图1  含水率w不同时兰州黄土应变-应力关系曲线

Fig. 1  Strain and stress curves of Lanzhou loess at different water content

2  割线模量与含水率关系曲线

根据侧限压缩试验获得的数据分别绘制不同压力下原状黄土与重塑黄土的割线模量E_d与含水率w关系曲线，如图2所示。

由图2可见：不同含水率条件下，原状黄土的割线模量变化区间为2 615~16 393 kPa, 重塑黄土的割线模量变化区间为974~10 309 kPa。在不同压力条件下原状样和重塑样的割线模量与含水率关系曲线均分布在较小的区域内，但二者存在一定差异。不同压力条件下原状样割线模量与含水率关系曲线存在交叉，而重塑样的曲线则近似平行。

造成上述差异的原因是原状样存在明显的结构强度。侧限压缩试验下原状样在应变-应力曲线第一拐点(对应结构强度)之前压力作用下土体的压力未达到土体保持自身结构的最大压力即结构强度，应变-压力关系近似呈线性关系，且增长速度总体上较小，而割线模量是应变与压力之比的倒数，故在第一拐点之前原状样的割线模量总体上较大，即当压力较小时，原状样割线模量与含水率关系曲线在图中位置较高；在第一拐点之后，压力作用下土体内压力超过了结构强度，土体自身结构破坏，随压力的增大土体变形加剧，应变-压力关系呈非线性并在总体上以较大速度增大，故此时原状样的割线模量总体上较小，即当压力不太大时，原状样割线模量与含水率关系曲线在图中位置反而较低；当达到第二拐点之后，应变-压力关系曲线趋于平缓，故此时原状样的割线模量再次增大，即当压力较大时，原状样割线模量与含水率关系曲线在图中位置升高。同时，土体的第二拐点出现还与含水率有关。当原状样的含水率为5%时，应变-压力关系曲线无明显第二拐点，但在第一拐点之后，其应变随压力的增长速度明显减小，如图1(a)所示，故当含水率为5%时其割线模量随压力的增大而增大，如图2(a)中含水率为5%时所示。而当含水率大于等于12%时，应变-压力关系曲线具有明显双拐点，且第一拐点后应变随压力增长速度较大，第二拐点后应变-压力关系曲线趋于平缓，此时割线模量随压力的增大呈现先减小后增大的特点，如图2(a)所示。故不同压力条件下原状样的割线模量与含水率关系曲线出现交叉。

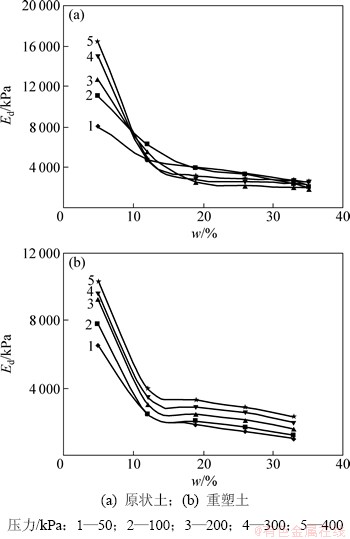
图2  兰州黄土割线模量E_d-含水率w曲线

Fig. 2  Secant modulus and water content curves of Lanzhou loess

对于重塑黄土，由于不具有明显的结构强度，故其割线模量随压力的变化规律相对简单，即随压力的增大而增大，表现为不同压力条件下重塑样的割线模量与含水率关系曲线则近似平行。

在不同压力下，原状样和重塑样的割线模量随含水率的增长均呈非线性递减趋势。在含水率较小(w＜12%)时，割线模量递减的速度随含水率增大很快；当含水率较大时，割线模量递减的速度随含水率增大趋于平缓。

不同压力条件下割线模量与含水率的关系呈现近似于双曲线的函数关系，可用下式描述：

             (1)

式中：a，b和c为拟合系数。

采用式(5)对兰州原状土和重塑土的割线模量与含水率关系进行拟合，拟合结果如表2所示。

表2  割线模量与含水率拟合参数

Table 2  Fitting parameters of secant modulus and water content

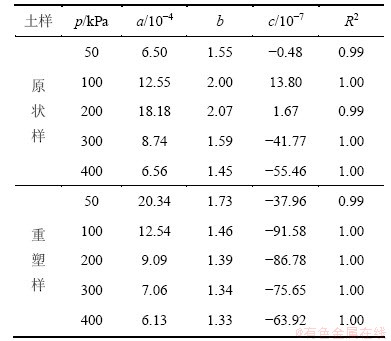
由表2可见：拟合获得的可决系数R²在0.99以上，说明采用式(1)描述不同压力条件下兰州黄土割线模量与含水率的关系具有合理性。

3  含水率对结构性参数影响的单变量模型

3.1  模型构建

通过释放结构势的方法寻求结构性的定量化指标是采用土力学方法构建土结构性参数的主要思想。基于应变的土结构性参数其表达式为

               (2)

式中：m_p为基于应变的土结构性参数；ε_o为应力σ下原状土体的应变；ε_s为应力σ下原状饱和土体的应变；ε_r为应力σ下重塑土体的应变。

考虑到ε_o，ε_s和ε_r为同一应力σ下土体的应变，可化简得到

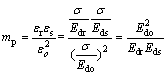        (3)

式中：σ为土体的应力；E_do为应力σ下原状土体的割线模量；E_ds为应力σ下原状饱和土体的割线模量；E_dr为应力σ下重塑土体的割线模量。

对于不同含水率的土体，对应于相同压力时其割线模量也不同，若将土体的割线模量与含水率之间具有的相关性记作

                  (4)

将式(4)代入式(3)，则可获得含水率对结构性参数影响的单变量模型通式：

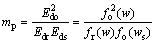          (5)

式中：f_o(w)为压力p(对应的土体应力为σ)下原状土体的割线模量与含水率关系式；f_r(w)为压力p(对应的土体应力为σ)下重塑土体的割线模量与含水率关系式；f_o(w_s)为压力p(对应的土体应力为σ)下饱和原状土体的割线模量与含水率关系式。

由式(5)可见：只要能够确定不同土体的E=f(w)的具体表达式，式(5)就能够具体确定。将第2节中获得的不同压力条件下割线模量与含水率的关系式(1)代入式(5)，则可以获得含水率对结构性参数影响的单变量模型：

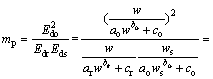
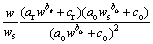        (6)

式中：a_o，b_o和c_o为原状样割线模量与含水率关系的拟合参数；a_r，b_r和c_r为重塑样割线模量与含水率关系的拟合参数；w_s为饱和含水率。

注意到饱和原状样的割线模量仅是原状样割线模量与含水率关系中的一个特定状态，故式(6)中饱和原状样割线模量与含水率关系的拟合系数与原状样的相同。

构建含水率对结构性参数影响规律模型的积极意义在于由于涉及的单变量是含水率，故能够直观地反映含水率对土体结构性的影响规律；所获得的模型利于进行数值计算，也使得含水率对结构性参数影响规律的研究由定性分析转入定量分析。

3.2  含水率对结构性参数影响的单变量模型检验与分析

在分析含水率与结构性参数之间关系时，通常的作法是先直接读取试验数据，然后代入式(2)计算获得不同的点，再按照含水率进行排列，可将由式(2)获得的点视为实测值。采用式(6)可以直接计算获得不同含水率下土结构性参数m_p，可将由式(6)计算获得的结果视为计算值。通过比较实测值与计算值，检验含水率对结构性参数影响的单变量模型。

对兰州黄土侧限压缩试验数据整理后绘制不同压力条件下结构性参数m_p的实测值和计算值，如图3所示。

由图3可以看出：由式(6)获取的计算值和式(2)获取的实测值能够较好地吻合，说明所构建的含水率对结构性参数影响的单变量模型具有一定的合理性。由图3还可以看出：不同压力条件下结构性参数随含水率的增大呈递减趋势。但随着压力条件的不同，这种递减趋势存在差异，当应力较小(p=50 kPa)时，随含水率增大，结构性参数递减的趋势较平缓；当压力较大(p≥200 kPa)时，随含水率增大，结构性参数呈快速递减趋势。在这两者之间则呈现出先平缓递减后快速递减的过渡状态。

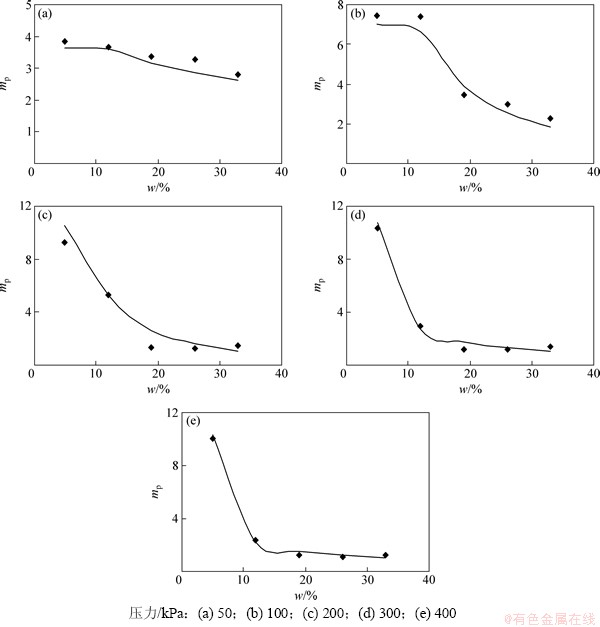
图3  结构性参数计算值与实测值关系

Fig. 3  Relationship between calculated and test values of structural parameter

产生上述现象的原因在于：含水率和压力直接影响土体的结构。随着含水率增大，土体颗粒间胶结和吸力逐渐弱化，土体结构受损，结构强度减小(第一拐点前移)，但当压力较小且土体内应力未达到结构强度时，土体结构虽然发生损伤但仍能够保持自身结构不被完全破坏，故在较小的压力条件下结构性参数随含水率的增大呈缓慢减小的趋势。当压力较大时，土体内应力一旦超过了结构强度，土体自身结构完全破坏，变形突增，土体受压密实，土体结构的可变性减小，土体结构性骤减，故在较大的压力下结构性参数随含水率的增大呈快速减小的趋势。当压力介于上述二者之间，且含水率较小时，土体内应力未达到土体结构强度，土体结构虽然发生损伤但仍能够保持自身结构的不被完全破坏，土体结构性缓慢减弱；当含水率较大时，土体结构强度随之减弱，土体内应力达到并超出了土体结构强度，土体结构性骤减；故当压力介于上述二者之间时，结构性参数随含水率的增大呈现出先平缓递减后快速递减的过渡状态。

4  结论

(1) 不同压力下原状样和重塑样的割线模量均随含水率增大而呈递减趋势，但二者之间存在差异。原状样割线模量与含水率关系曲线存在交叉，而重塑样的曲线则近似平行。造成这种差异的原因是原状样存在明显的结构强度。

(2) 构建了含水率对结构性参数影响的单变量模型，并对其进行检验。该模型以含水率作为单变量,能够直观地反映含水率对土体结构性的影响规律，利于实现数值计算。

(3) 不同压力条件下结构性参数随含水率的增大呈递减趋势。但随着压力条件的不同，这种递减趋势存在差异。当压力较小时，结构性参数随含水率递减的趋势较平缓；当压力较大时，结构性参数随含水率递减的趋势是快速递减。在这两者之间则呈现出先平缓递减后快速递减的过渡状态。

参考文献：

[1] 谢定义, 齐吉琳. 土结构性及其定量化参数研究的新途径[J]. 岩土工程学报, 1999, 21(6): 651-656.

Xie dingyi, Qi jilin. soil structure characteristics and new approach in research on its quantitative parameter[J]. Chinese journal of Geotechnical Engineering, 1999, 21(6): 651-656.

[2] Terzaghi K. Theoretical soil mechanics[M]. New York: Weley, 1943: 1-6.

[3] Skempton A W. Note on the compressibility of clays[J]. Q J Geological Soc, 1994(100): 119-135.

[4] Skempton A W. The consolidation of clays by gravitational compaction[J]. Quarterly Journal of Geology Society, 1970, 125: 373-411.

[5] Levoueil S, Vaughan P R. The general and congruent effects of structure in natural soil and weak rock[J]. Geotechnique, 1990, 40(3): 467-488.

[6] 齐吉琳. 土的结构性及其定量化参数的研究[D]. 西安:西安理工大学土木建筑工程学院, 1999: 15-20.

Qi jilin. Soil structure characteristics and study of its quantitative parameter[D]. Xi’an: Xi’an University of Technology. School of Civil Engineering and Architeture, 1999: 15-20.

[7] 谢定义, 姚仰平, 党宁发. 高等土力学[M]. 北京: 高等教育出版社, 2008: 34-35.

xie dingyi, yao yangping, dang ningfa. advanced soil mechanics[m]. Beijing: higher Education Press, 2008: 34-35.

[8] 邵生俊, 陶虎, 许萍. 黄土结构性力学特性研究与应用的探讨[J]. 岩土力学, 2011, 32(S2): 42-48.

SHAO Shengjun, TAO Hu, XU Ping. Discussion on research of mechanical characteristics of loess considering structural behavior and its application[J]. Rock and Soil Mechanics, 2011, 32(S2): 42-48.

[9] 沈珠江. 土体结构性模型—21世纪土力学的核心问题 [J]. 岩土工程学报, 1996, 18(1): 95-97.

SHEN Zhujiang. Mathematics model of soils structure—The key issue of 21th century soil mechanics[J]. Chinese journal of Geotechnical Engineering, 1996, 18(1): 95-97.

[10] 骆亚生, 张爱军. 黄土结构性的研究成果及其新进展[J]. 水力发电学报, 2004, 23(6): 66-69.

Luo Yasheng, Zhang aijun. outcomes research of loess and its new advance[J]. Journal of Hydroelectric Engineering, 2004, 23(6): 66-69.

[11] 谢定义, 齐吉琳, 朱元林. 土的结构性参数及其与变形强度的关系[J]. 水利学报, 1999, 30(10): 1-6.

XiE Dingyi, QI Jilin, ZHU Yuanlin. The parameter of soil structure and the relationship of it with deformation and strength of soil[J]. journal of Hydraulic engineering, 1999, 30(10): 1-6.

[12] 邵生俊, 周飞飞, 龙吉勇. 原状黄土结构性及其定量化参量研究[J]. 岩土工程学报, 2004, 26(4): 531-536.

Shao shengjun, Zhou Feifei, Long Jiyong. Study of the structural and quantitative parameters of undisturbed loess[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(4): 531-536.

[13] 邵生俊, 龙吉勇, 于清高, 等. 湿陷性黄土的结构性参数本构模型[J]. 水利学报, 2006, 37(11): 1315-1322.

SHAO Shengjun, LONG Jiyong, YU Qinggao, et al. A constitutive model of collapsible loess with structural parameter[J]. Journal of Hydraulic Engineering, 2006, 37(11): 1315-1322.

[14] 骆亚生, 谢定义, 邵生俊, 等. 复杂应力条件下的土结构性参数[J]. 岩石力学与工程学报, 2004, 23(24): 4248-4251.

Luo Yasheng, XIE Dingyi, Shao Shengjun. Soil structural parameters under complex stress conditions[J]. Rock Mechanics and Engineering, 2004, 23(24): 4248-4251.

[15] 骆亚生, 谢定义. 复杂应力条件下土的结构性本构关系[J]. 四川大学学报(工程科学版), 2005, 37(5): 14-18.

LUO Yasheng, XIE Dingyi. Structural constitutive relation of soils under complex stress conditions[J]. Journal of Sichuan University (Engineering Science), 2005, 37(5): 14-18.

[16] 夏旺民. 黄土弹塑性损伤本构模型及工程应用研究[D]. 西安: 西安理工大学土木建筑工程学院, 2005: 17-29.

Xia wangmin. Loess elastoplastic damage constitutive model and engineering application[D]. Xi’an: Xi’an University of Technology. School of Civil Engineering and Architeture, 2005: 17-29.

[17] 陈存礼, 高鹏, 何军芳. 考虑结构性影响的原状黄土等效线性模型[J]. 岩土工程学报, 2007, 29(9): 1330-1336.

Chen Cunli, Gao Peng, He Junfang. Undisturbed loess taking into account the structural effects of the equivalent linear model[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(9): 1330-1336.

[18] 陈存礼, 胡再强, 高鹏. 原状黄土的结构性及其与变形特性关系研究[J]. 岩土力学, 2006, 27(11): 1891-1896.

Chen Cunli, HU Zaiqiang, Gao Peng. Structural and deformation characteristics of undisturbed loess[J]. Rock and Soil Mechanics, 2006, 27(11): 1891-1896.

[19] 陈存礼, 高鹏, 胡再强. 黄土的增湿变形特性及其与结构性的关系[J]. 岩石力学与工程学报, 2006, 25(7): 1352-1360.

Chen Cunli, Gao Peng, Hu Zaiqiang. Moistening deformation characteristics and its structural relationship of the loess[J]. Rock Mechanics and Engineering, 2006, 25(7): 1352-1360.

[20] 冯志焱. 非饱和黄土结构性及有效应力动力等效粘弹性模型研究[D]. 西安: 西安理工大学土木建筑工程学院, 2006: 17-38.

FENG Zhiyan. Unsaturated loess structural and dynamic effective stress equivalent viscoelastic model[J]. Xi’an: Xi’an University of Technology. School of Civil Engineering and Architeture, 2005: 17-38.

[21] 陶虎, 邵生俊, 李小林, 等. 黄土的非饱和特征参数与结构性的试验研究[J]. 土木工程学报, 2012, 45(7): 148-153.

TAO Hu, SHAO Shengjun, LI Xiaolin, et al. Experimental study of the characteristic parameters and structural behavior of loess[J]. China Civil Engineering Journal, 2012, 45(7): 148-153.

[22] 田堪良, 张慧莉, 马俊. 基于强度条件的黄土结构性静力试验研究[J]. 岩土力学, 2012, 33(7): 1993-1999.

TIAN Kanliang, ZHANG Huili, MA Jun. Test study of loess structure based on static strength conditions[J]. Rock and Soil Mechanics, 2012, 33(7): 1993-1999.

[23] 蒋明镜, 胡海军, 彭建兵. 结构性黄土一维湿陷特性的离散元数值模拟[J]. 岩土力学, 2013, 34(4): 1121-1130.

JIANG Mingjing, HU Haijun, PENG Jianbing. Simulation of collapsible characteristics of structural loess underone- dimensional compression condition by discrete element method[J]. Rock and Soil Mechanics, 2013, 34(4): 1121-1130.

(编辑  何运斌)

收稿日期：2013-05-24；修回日期：2013-08-06

基金项目：国家自然科学基金资助项目(51178392)

通信作者：骆亚生(1967-)，男，陕西咸阳人，教授，博士，从事黄土静动力学特性及其工程应用研究；电话：029-87082038；E-mail：771545499@qq.com