基于均矢量相似性的机器学习样本集划分

陈先来^{1, 2}，杨路明¹

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；

2. 中南大学 湘雅医学院，湖南 长沙，410013)

摘  要：提出一种基于均矢量相似性的机器学习样本集分割方法(MSSS)，根据样本集中每个样本矢量与均矢量之间的余弦相似性，将样本划分成训练集和测试集。为评价MSSS方法性能，分别用随机分割法(RSS)和MSSS方法，按不同比例划分来自UCI的4个数据集，对产生的训练集-测试集进行Hotelling T²检验；另外，采用得到的训练集对分类BP神经网络进行训练，以相应的测试集测试神经网络。研究结果表明：对用RSS划分4个数据集产生的训练集-测试集进行Hotelling T²检验，发现均存在F值超出界值的现象，而MSSS均未出现；使用MSSS训练的神经网络所产生的训练-测试误差差异、准确率差异均比使用RSS训练的神经网络所产生的小，说明用MSSS划分产生的训练集与测试集的一致性比用RSS划分产生的好。

关键词：均矢量；样本集分割；相似性；机器学习

中图分类号：TP18          文献标志码：A         文章编号：1672-7207(2009)06-1636-06

Partitioning machine learning sample set using similarity to mean vector

CHEN Xian-lai^{1, 2}, YANG Lu-ming¹

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. Xiangya School of Medicine, Central South University, Changsha 410013, China)

Abstract: MSSS (Mean-similarity-based splitting sample), an algorithm for partitioning machine learning sample set, was presented based on similarity to mean vector. A sample set was splited into training set and test set by cosine similarity of each sample vector to mean vector. Simulation study were set up to evaluate MSSS. Four data sets from UCI were individually split by different proportions with MSSS and randomly splitting sample (RSS). The training set and test set were tested by Hotelling T². Back propagation neural networks for classification were built up. Training set was used for training networks and test set for testing networks. The result shows that the F value of Hotelling T² test for RSS might overtop its border, but that for MSSS does not. In contrast with RSS, MSSS has significantly lower error difference between training error and test error and accuracy difference between training accuracy and test accuracy of the network. It can be confirmed that the consistency between training set and test set from MSSS is superior to that from RSS.

Key words: mean vector; splitting sample set; similarity; machine learning

学习算法和学习样本是影响机器学习质量的主要因素。样本是机器学习的数据基础，当训练样本数量达到一定程度时，它对识别率的影响不大，造成识别率波动的主要因素是样本分布的不同^[1]。样本集是否具有代表性，决定了机器学习的效果。有效分割样本集，提高训练样本质量，对于改善机器学习质量有着十分重要的意义。机器学习时，一般将样本划分为训练集和测试集。训练集的代表性越强，所得模型质量越好。当总样本确定时，训练集的质量则取决于样本抽取方法。最常用的样本集分割方法是随机样本分割法(Randomly splitting sample，RSS)，它实现简单，易于理解，但随机性强，稳定性差。对于非随机分割方法，Lindenbaum等^[2]提出了一种用于最近邻分类器训练的样本选择LSS算法，试图找出对分类结果影响最大的样本；郝红卫等^[3]基于最近邻方法提出了一种神经网络训练样本选择方法；Mitra等^[4]提出了基于密度的多尺度数据浓缩方法；张莉等^[5-6]采用聚类方法进行了样本分割研究；冯楠等^[7]提出了基于遗传算法的样本划分方法。这些方法在提高样本集分割质量方面取得了较好的效果，但计算方法比较复杂。在此，本文作者提出一种基于均值相似性的样本分割方法(Mean-similarity-based splitting sample，MSSS)，对MSSS和RSS样本集分割方法进行实验仿真研究。

1  相关理论

1.1  样本及其矢量表示

1个样本由若干个变量项组成，将每个变量项看成1个分量时，该样本就可表示为由这些分量组成的矢量。对应的样本集则可以表示为由样本矢量组成的集合，即样本集S可以表示成一个矢量空间S={s₁, s₂, …, s_i, …, s_n}，s_i为单个样本。

设样本包含k个变量项，每个样本则是1个k维的矢量，s_i=(x_i1, x_i2, …, x_ij, …, x_ik)，x_ij为矢量s_i的第j个分量，n个样本形成的样本集可用矢量空间S来表示：

1.2  矢量相似性的计算

度量矢量相似性的常用方法有夹角余弦系数和欧氏距离等。夹角余弦系数度量是根据2个矢量间夹角的余弦来进行测量的。如图1所示，将样本表示成k维空间中的模式矢量后，2个模式矢量s_p和s_q在模式空间中形成夹角θ_pq。2个样本的相似度越大，则2个矢量间的夹角越小，夹角余弦系数越接近1。基于夹角余弦系数的相似性度量在文档处理、图像与信号处理等方面有着广泛应用^[8-10]。

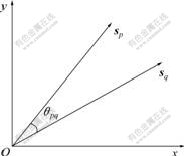
图1  2个矢量s_p和s_q之间的夹角

Fig.1  Angle between vector s_p and s_q

设矢量s_p=(x_p1, x_p2, …, x_pj, …, x_pk)，s_q=(x_q1, x_q2, …, x_qj, …, x_qk)，2个矢量s_p和s_q之间的相似性可用夹角余弦系数公式计算：

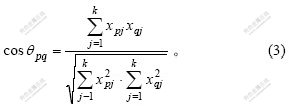
2  基于均矢量相似性的样本集分割

均值是各样本的平均取值，是总样本整体特性的一种反映。个体样本矢量与均矢量之间的相似性，反映了个体样本与总样本之间的相似关系，若相似性越大，则越接近样本集的总体特性。因此，样本集中个体的分布情况可以通过个体矢量与均矢量之间的相似性反映出来。根据样本矢量与均矢量之间的相似性，选择训练样本，可以使总样本中的样本分布信息较好地体现到所抽取的训练集中，从而提高机器学习样本集的质量。基于这种思想，本文作者提出一种基于均矢量相似性的机器学习样本集分割算法(MSSS)。该算法的具体步骤描述如下。

输入：待分割的样本集S={s₁, s₂, …, s_i, …，s_n}

输出：抽取的样本子集S′={s₁′, s₂′, …, s_l′, …, s_m′}

步骤1：输入待分割样本集S。

步骤2：按式(2)计算出总样本集的均矢量。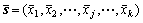

步骤3：按式(3)计算每个样本矢量s_i与均矢量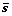之间的相似性。

步骤4：按样本矢量的相似性和所属分类类别将样本集排序。

步骤5：根据样本抽取数量m将排序的总样本集分割为m段。

步骤6：抽取每段中间位置的样本s_l′。

步骤7：输出由所抽取样本s_l′组成的样本子集S′= {s₁′, s₂′, …, s_l′, …, s_m′}为分割产生的样本集。

由此可见，MSSS总算法的时间复杂度为O(1)，其空间复杂度与待划分样本集的样本量及变量项数量有关，样本、变量项的数量越多，时间开销越大。对于MSSS划分产生的样本集质量，可通过与RSS划分产生的样本集进行实验对比来评价。

3  实验仿真评价

3.1  数据来源与预处理

采用UCI机器学习数据仓库中分类数据库Breast cancer，Iris，Vehicle和Wine作为实验仿真数据即样本集，删除带缺失值的记录。数值型数据按照式(4)进行归一化处理，使数据取值范围在[0，1]之间，以满足分类神经网络的要求。离散型数据，用二进制编码进行转换后作数值型数据处理。

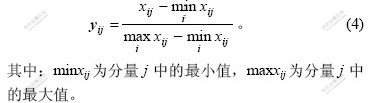
3.2  数据的划分

预处理后的样本集，采用RSS和MSSS 2种方法按25%，50%和75%的比例抽取训练集，剩余样本作为测试集。采用RSS按每种比例划分10次，产生10个样本集。采用MSSS法按每种比例划分1次，产生1个样本集。

3.3  Hotelling T²检验

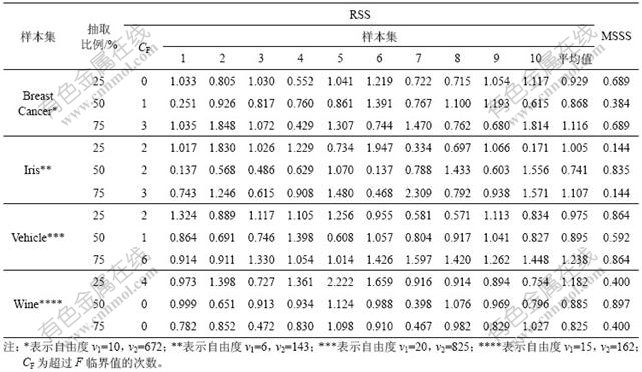
为评价RSS和MSSS 2种分割方法的优劣，对所产生的训练集、测试集进行Hotelling T²检验，得到的F值如表1所示。

表1  RSS和MSSS的Hotelling T²检验的F值

Table 1  F value of Hotelling T² test for RSS and MSSS

3.4  分类神经网络训练检验

分类BP神经网络是一种常用的机器学习算法，应用于生物医学、电力、交通等领域^[11-14]。衡量分类神经网络训练效果的主要指标是误差和分类准确率。网络模型对训练集的误差为训练误差(Training error)，对测试集的误差为测试误差(Test error)，两者之差为误差差异(Error difference)，用?E表示。相应地，分类准确率有训练准确率(Training correct rate)和测试准确率(Test correct rate)，两者之差为准确率差异(Correct rate difference)，用?R表示。这2种差异除反映神经网络模型本身的泛化能力外，还反映用于模型构建的测试集与训练集之间的差异性。利用所训练的分类BP神经网络的误差差异和准确率差异可以评价测试集与训练集之间的一致性。

在本研究中，神经网络采用常用的3层结构，其中：输入层、输出层结点数由样本集的实际情况决定， 隐层结点数按公式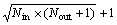 确定，N_in为输入结点数，N_out为输出结点数，学习率分别取0.2和0.15，激活函数采用标准的Sigmoid函数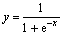。利用划分出来的数据集，对所构建的分类BP神经网络进行训练和测试，迭代训练5 000次。为保证评价的信度，每个训练集分别建立10个网络模型，网络的误差差异和准确率差异取平均值。

采用4个数据库通过RSS和MSSS方法按50%比例抽取产生的训练集和测试集，在神经网络训练迭代到不同次数时产生的在线误差差异和准确率差异如图2~5所示，离线时误差差异和准确率差异如表2所示。表2中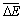：为离线平均误差差异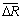；为离线平均准确率差异。

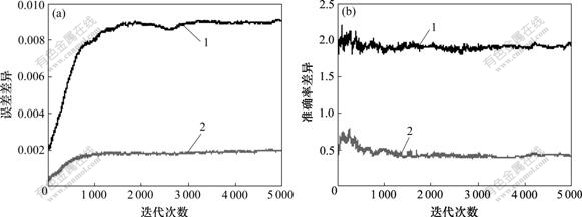
(a) 误差差异；(b)准确率差异

1—RSS；2—MSSS

图2  样本集Breast cancer的神经网络误差差异和准确率差异

Fig.2  On-line error difference and correct rate difference of neural network for sample set Breast cancer

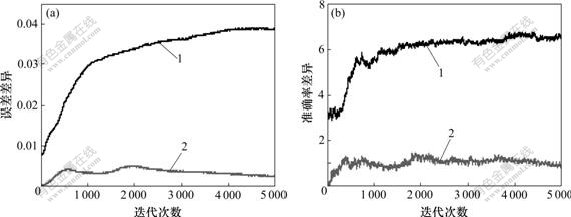
(a) 误差差异；(b) 准确率差异

1—RSS；2—MSSS

图3  样本集Iris的神经网络误差差异和准确率差异

Fig.3  On-line error difference and correct rate difference of neural network for sample set Iris

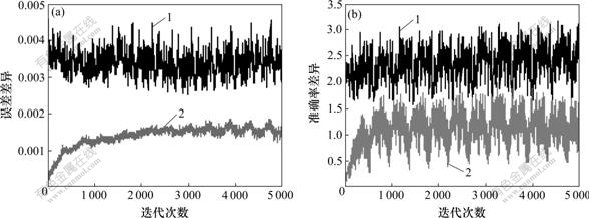
(a) 误差差异；(b) 准确率差异

1—RSS；2—MSSS

图4  样本集Vehicle的神经网络误差差异和准确率差异

Fig.4  On-line error difference and correct rate difference of neural network for sample set Vehicle

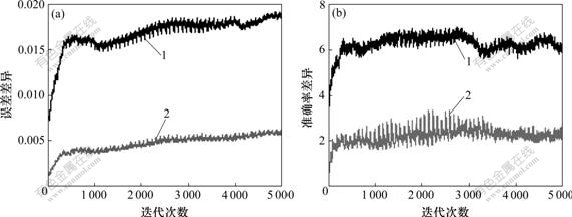
(a) 误差差异；(b) 准确率差异

1—RSS；2—MSSS

图5  样本集Wine的神经网络在线误差差异和准确率差异

Fig.5  On-line error difference and correct rate difference of neural network for sample set Wine

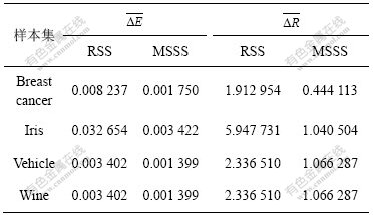
表2  神经网络离线误差差异和离线准确率差异

Table 2  Off-line error difference and correct rate difference of neural network

4  分析与讨论

Hotelling T²检验可以检测两组数据间的差异显著性，若F值大于临界值，则说明2组数据间存在显著性差异，相反，则说明2组数据间无显著性差异，一致性好^[15]。从表1可见：MSSS方法划分产生的训练集-测试集F值均小于相应的F临界值，RSS方法划分产生的训练集-测试集F值则存在大于F临界值现象。其中，Iris和Vehicle 2个样本集采用RSS方法按25%，50%和75%的比例抽取训练样本，F值超过临界值的概率很大(分别为2/10，2/10，3/10和3/10，1/10，6/10)，对另外2个数据库的划分也存在这种现象。结果说明：MSSS方法产生的训练集-测试集之间无显著性差异，一致性比RSS方法的好。

训练集与测试集的一致性还可以从训练分类神经网络所得到的误差差异和准确率差异反映出来，这2项指标越大，说明所建立的神经网络泛化能力越弱，训练集与测试集的一致性也越差。对用RSS和MSSS方法划分的样本集进行分类神经网络检验，发现：对于所选择的4个样本集，RSS方法产生的在线和离线误差差异、准确率差异均比MSSS方法产生的大。可见，MSSS方法与RSS方法相比，所产生的训练集、测试集的一致性更好。利用MSSS方法产生的训练集所建立的神经网络模型，与利用RSS方法产生的训练集所建立的神经网络模型相比，泛化能力更强。

5  结  论

a. 利用均矢量，可以有效地将样本集划分为训练集和测试集。

b. 采用MSSS方法划分得到的训练集-测试集之间的一致性好，无显著差异。

c. 与RSS方法相比，MSSS方法更稳定。用MSSS得到的结果是稳定的，不受时间、运行环境等因素影响。

d. 利用MSSS方法划分产生的训练集建立的BP神经网络模型，比利用RSS方法划分产生的训练集建立的BP神经网络模型泛化能力强。

参考文献：

[1] 刘 刚, 张洪刚, 郭 军. 不同训练样本对识别系统的影响[J]. 计算机学报, 2005, 28(11): 1923-1928.
LIU Gang, ZHANG Hong-gang, GUO Jun. The influence of different training samples to recognition system[J]. Chinese Journal of Computers, 2005, 28(11): 1923-1928.

[2] Lindenbaum M, Markovitch S, Rusakov D. Selective sampling for nearest neighbor classifiers[J]. Machine Learning, 2004, 54(2): 125-152.

[3] 郝红卫, 蒋蓉蓉. 基于最近邻规则的神经网络训练样本选择方法[J]. 自动化学报, 2007, 33(12): 1247-1251.
HAO Hong-wei, JIANG Rong-rong. Training sample selection method for neural networks based on nearest neighbor rule[J]. Acta Automatica Sinica, 2007, 33(12): 1247-1251.

[4] Mitra P, Murthy C A, Pal S K. Density-based multiscale data condensation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(6): 734-747.

[5] 张 莉, 郭 军. 基于边界样本的训练样本选择方法[J]. 北京邮电大学学报, 2006, 29(4): 77-80.
ZHANG Li, GUO Jun. A method for the selection of training samples based on boundary samples[J]. Journal of Beijing University of Posts and Telecommunications, 2006, 29(4): 77-80.

[6] 薛志东, 王 燕, 邱德红. 逆C 均值学习样本筛选方法[J]. 微计算机信息, 2007, 23(27): 209-210.
XUE Zhi-dong, WANG Yan, QIU De-hong. An inverse C-mean method for filtering the learning samples[J]. Microcomputer Information, 2007, 23(27): 209-210.

[7] 冯 楠, 方德英, 解 晶. 一种基于遗传算法的样本集数据分割方法[J]. 计算机工程与应用, 2008, 44(16): 129-131.
FENG Nan, FANG De-ying, XIE Jing. Method of data splitting for sample set based on genetic algorithms[J]. Computer Engineering and Applications, 2008, 44(16): 129-131.

[8] Friedman M, Last M, Makover Y, et al. Anomaly detection in Web documents using crisp and fuzzy-based cosine clustering methodology[J]. Information Sciences, 2007, 177(2): 467-475.

[9] DONG Yong-gui, SUN Zhao-yan, JIA Hui-bo. A cosine similarity-based negative selection algorithm for time series novelty detection[J]. Mechanical Systems and Signal Processing, 2006, 20(6): 1461-72.

[10] Arnia F, Iizuka I, Fujiyoshi M, et al. DCT sign-based similarity measure for JPEG image retrieval[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2007, E90-A(9): 1976-1985.

[11] 陈先来, 肖晓旦, 杨 荣, 等. 基于误差反向传播神经网络的胃癌细胞识别研究[J]. 中国循证医学杂志, 2007(9): 637-640.
CHEN Xian-lai, XIAO Xiao-dan, YANG Rong, et al. Research on recognizing gastric cancer cell based on back propagation neural network[J]. Chinese Journal of Evidence-based Medicine, 2007(9): 637-640.

[12] Mcmahon E M, Korinek J, Yoshifuku S, et al. Classification of acute myocardial ischemia by artificial neural network using echocardiographic strain waveforms[J]. Computers in Biology and Medicine, 2008, 38(4): 416-424.

[13] 宋晓华, 李彦斌, 韩金山, 等. 对传神经网络算法的改进及其应用[J]. 中南大学学报: 自然科学版, 2008, 39(5): 1059-1063.
SONG Xiao-hua, LI Yan-bin, HAN Jin-shan, et al. An improved counter propagation networks and its application[J]. Journal of Central. South University: Science and Technology, 2008, 39(5): 1059-1063.

[14] Swift D K, Dagli C H. A study on the network traffic of connexion by boeing: Modeling with artificial neural networks[J]. Engineering Applications of Artificial Intelligence, 2008, 21(8): 1113-1129.

[15] 颜 虹. 医学统计学[M]. 北京: 人民卫生出版社, 2005: 284-298.
YAN Hong. Medical statistics[M]. Beijing: People’s Medical Publishing House, 2005: 284-298.

收稿日期：2008-11-10；修回日期：2009-03-27

基金项目：国家自然科学基金资助项目(60873204)

通信作者：陈先来(1970-)，男，湖南新田人，副教授，从事数据挖掘与决策支持系统研究；电话：0731-82650242；E-mail: chenxianlai@xysm.net