DOI: 10.11817/j.ysxb.1004.0609.2021-35962
Ti55合金电辅助V弯电热力耦合仿真及回弹预测
李 萍，解修明，汪会干，严思梁，薛克敏
(合肥工业大学 材料科学与工程学院，合肥 230009)
摘 要：本文为研究Ti55合金板材电辅助V弯回弹规律，基于ABAQUS软件平台建立Ti55合金板材电辅助V弯电-热-力耦合三维有限元模型。对板材V弯及回弹过程进行正交试验模拟，研究弯曲角、相对弯曲半径、有效电流密度、成形速度对板材回弹的影响规律，建立了基于径向基函数的回弹预测模型。结果表明：在选取参数范围内，随着弯曲角、相对弯曲半径的增大和有效电流密度的减小，回弹角增大；随着成形速度的增大，回弹角先减小后增大。极差分析和方差分析得到弯曲角和相对弯曲半径对回弹角有显著影响。电辅助板材V弯相对机械V弯回弹角平均降低48.7%。进行电辅助V弯实验，对比厚度、温度和回弹角，平均误差分别为9.4%、4.6%和13.4%，验证了有限元模拟及回弹预测模型的准确性。
关键词：钛合金；电辅助；回弹预测；有限元模拟
文章编号：1004-0609(2021)-04-0847-11 中图分类号：TG306 文献标志码：A
引文格式：李 萍, 解修明, 汪会干, 等. Ti55合金电辅助V弯电热力耦合仿真及回弹预测[J]. 中国有色金属学报, 2021, 31(4): 847-857. DOI: 10.11817/j.ysxb.1004.0609.2021-35962
LI Ping, XIE Xiu-ming, WANG Hui-gan, et al. Electric-thermal-mechanical coupled simulation and springback prediction of Ti55 alloy electrical assisted V-bending[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(4): 847-857. DOI: 10.11817/j.ysxb.1004.0609.2021-35962
钛合金由于比强度高、密度低、耐高温而广泛应用于航空航天领域[1-2]。Ti55钛合金是我国自主研发的近α型钛合金，添加了稀土元素Nd，具有良好的强度、抗蠕变性能和热稳定性能，能在550 ℃下长期服役[3]。钛合金属于室温下难成形金属，且钛合金板材在冷冲压时易开裂、需要较大的成形力[4]；且由于其高强度、低弹性模量而导致的高弹性回复，从而导致Ti55板材成形会产生较大回弹，影响材料的成形精度。
通常采用热加工工艺提高难变形板材的成形性能。WANG等[5]进行镁合金在各种温度下的V弯成形，研究发现，温度越高，回弹量越小。白雪飘等[6]在高温下进行钛合金成形极限实验，建立热态成形极限；研究表明，随着温度的升高，钛合金的成形极限增加。MAENO等[7]采用局部接触加热的方法对坯料进行热冲压成形，研究表明，局部接触加热的极限拉深比全炉加热的极限拉深大。GISARIO等[8]利用激光加热弯曲处，能够显著减少钛合金板材V弯的回弹量。但传统热加工工艺时间长，加热效率低，钛合金化学活性高，易氧化，显著降低Ti55合金薄板成形质量。
电辅助成形是指在金属塑性成形的过程中引入脉冲电流，利用电流的电致塑性效应来降低流动应力，提高成形极限的一种成形方法[9]。电辅助成形技术因为效率高、成形质量好，而受到越来越多的关注[10]。XIE等[11]研究了脉冲频率、峰值电流对合金板材V弯回弹的影响，实验表明脉冲频率、峰值电流越大、回弹角越小。李超等[12]将脉冲电流引入到AZ31镁合金板材材料的气胀成形过程中，提高了板材的气胀成形极限。ZHAO等[13]进行了电辅助U形弯曲实验，研究电参数占空比对板材回弹的影响，结果表明，30%的占空比U形弯曲回弹比室温下成形回弹降低50%。官英平等[14]通过对弯曲力和弯曲行程的实时监测，根据塑性弯曲理论和神经网络技术，实现了材料性能参数的实时识别和最优工艺参数的实时预测。李金华等[15]分析了钛合金板材激光弯曲成形过程中各参数对回弹的影响，并用最小二乘法进行预测。韩江等[16]建立自由折弯板料成形回弹的径向基函数近似模型，对回弹角度有较高的预测精度。穆雪峰[17]运用多种近似方法对描述机翼展向升力分布的代理模型进行构造，结果显示径向基函数模型在解决一般的高维非线性问题方面有很大的优势。
从以上分析可以看出，针对钛合金电辅助成形过程的回弹方面的研究工作多集中于定性实验，且尚缺乏电热力耦合加载状态下可靠的板材V弯回弹精确预测模型。因此，本文采用正交试验模拟方法研究不同弯曲角、相对弯曲半径、有效电流密度和成形速度的电辅助板材V弯成形回弹规律，并基于径向基函数建立回弹预测模型，以期为钛合金板材电辅助成形及回弹精确控制提供理论指导。
1 实验和模拟
实验采用1.6 mm的Ti55合金薄板。将坯料切割成150 mm×27 mm的矩形试样。材料成分如表1所示，初始材料的组织如图1 所示，为典型的网篮组织，相比钛合金的其他组织，室温强度和塑性介于等轴组织和魏氏组织之间，但网篮组织具有较好的高温持久性能、蠕变性能和断裂韧性，减少了弯曲开裂的可能性，从而具有较好的弯曲成形性[18-19]。
电辅助V弯实验装置如图2所示，包括V形凸凹模、上下绝缘板、两个铜电极。弯曲角为90°，凸模圆角半径为8 mm。直流脉冲发生器输出正脉冲信号，通过FLUKE红外热成像仪记录实验过程坯料温度变化。
表1 Ti55合金化学成分
Table 1 Chemical composition of Ti55 (mass fraction, %)
图1 Ti55初始组织
Fig. 1 Microstructure of as-received sheet
图2 实验装置
Fig. 2 Device of experiment
基于ABAQUS软件热-电-结构耦合模块对Ti55合金板材电辅助V弯及回弹过程进行模拟。有限元模型如图3所示。坯料的长宽为150 mm和27 mm，厚度设计为1 mm、1.6 mm和2 mm，凸模圆角半径设计为2 mm、5 mm和8 mm。
材料的物理性能参数定义如表2所示，通过不同温度、应变速率下单向拉伸实验得到其应力应变曲线，如图4所示。坯料和模具均选用热电结构耦合单元(Q3D8R)，坯料划分12000个六面体网格。
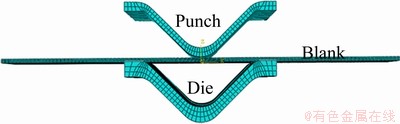
图3 板材V弯有限元模型
Fig. 3 FEM of sheet V-bending
表2 Ti55合金的物理性能参数[20]
Table 2 Physical properties of Ti55 alloy[20]
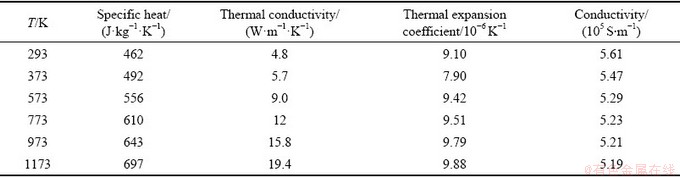
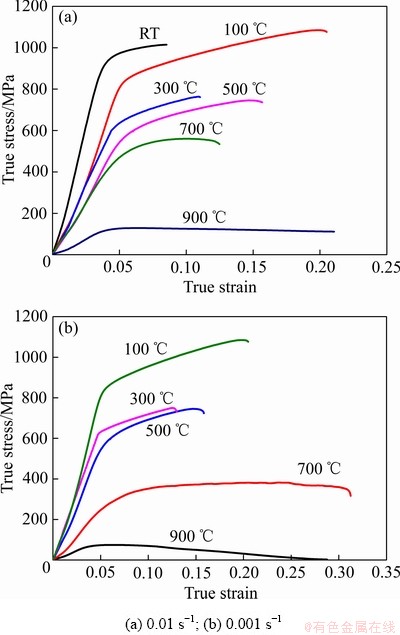
图4 不同应变速率下Ti55合金的应力-应变曲线
Fig. 4 Stress-strain curves of Ti55 alloy at different strain rates
在实际电辅助成形过程中，电流除了焦耳热效应，还有纯电塑性效应和磁效应。但相对于电流的焦耳热效应，电流的其他效应影响相对较小[21]，本文未予考虑。
边界条件：坯料、模具和环境初始温度设为室温(20 ℃)。凸模和凹模均定义为实体，坯料的辐射率设为0.68，坯料与模具之间的换热系数设置为100 W/(m2·K)。采用库仑摩擦条件，设置模具与坯料之间的摩擦因数为0.2。设置凸凹模的表面为主面，板材的表面为从面。表面电流载荷形式，在坯料一边设置面电流密度，一边设置电势为0。
Ti55钛合金对流换热系数计算[22-23]如式(1)所示：
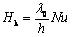(1)
式中：Hk为对流换热系数，W/(m2·K)；
为介质导热率，为 2.32×10-2 J/m/s/℃；h为工件尺寸；Nu为 Nusselt 数。
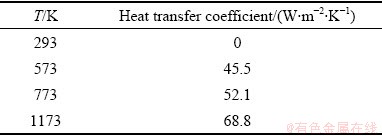
得到的换热系数如表3所示。
表3 坯料的对流换热系数
Table 3 Heat transfer coefficient of sheet
2 结果讨论
2.1 成形过程分析
Ti55合金板材成形过程如图5所示，在V弯成形的第一阶段，在凸模的作用下，坯料V弯处由弹性变形进入塑性变形；在成形的第二阶段，随着凸模向下移动，坯料下表面与凹模的斜面贴合在一起；在成形的第三阶段，坯料的两端接触凸模，随着凸模向下移动，坯料被反向弯曲，凸凹模之间的距离也在不断减小；在成形的第四阶段，凸模继续向下移动，直至凸凹模之间的距离为板厚，电辅助V弯成形过程结束。
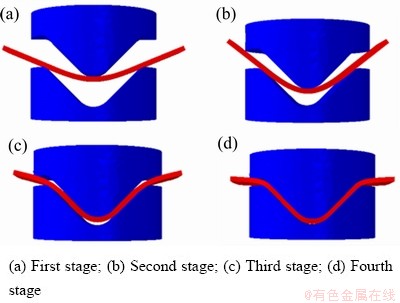
图5 电辅助板材 V弯成形过程图
Fig. 5 Process of electrical heating-assisted V-bending
在弯曲角90°、相对弯曲半径5、成形速度0.5 mm/s和有效电流密度3 A/mm2的条件下，模拟得到坯料上5个特征区域的等效应变随时间变化如图6所示。由图6可见，弯曲A处最先进入塑性阶段，塑性区域往B处蔓延；弯曲A处等效应变先迅速增加，后缓慢上升；C、E处始终处于弹性阶段，等效塑性应变为0；D处最后进入塑性阶段，且A处等效应变最大。
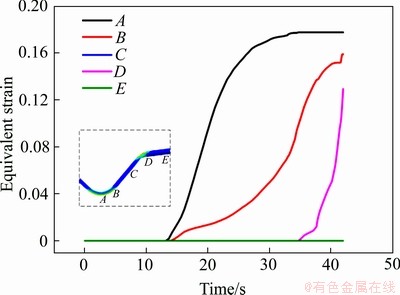
图6 电辅助V弯各特征点等效应变随时间变化图
Fig. 6 Variation of equivalent strain of each characteristic point with time of electric assisted V-bending
2.2 温度分布
本次实验脉冲电源输出电流波形为正脉冲矩形波，有效电流密度Jeff计算如式(2)所示：
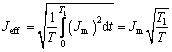(2)
式中：T是脉冲周期；T1是脉冲宽度；Jm是电脉冲幅值。本次模拟选用有效电流密度作为输入参数。
选取弯曲角90°、相对弯曲半径5和成形速度0.5 mm/s保持不变，改变有效电流密度大小，得到电辅助V弯各过程温度变化结果如下。
1) 在有效电流密度3~5 A/mm2下模拟单独的电辅助对坯料中间处一点温度随时间变化影响，如图7(a)所示。电流加热初始阶段，板材与环境间的温差较小，散失的热量很少，升温迅速。上升温度如式(3)所示：
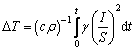(3)
式中：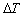
是平均温升；I是脉冲电流幅值；t是脉冲电流周期；S是试样的横截面积；
、
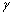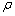、c分别是实验材料的比电阻、密度和比热。通过计算得到的温升和模拟结果相符。
当坯料的温度升高时，向外界散失的热量也增大，当两者相近时，坯料温度达到稳定值。在Ti55板材电辅助加热过程中，电流流经金属坯料，产生焦耳热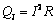
，一部分能量被转换成坯料的内能ΦS，使其温度升高；另一部分能量向外界散失[12]，能量散失的主要方式包括：高温坯料与低温模具间的热传导ΦCond；高温坯料对周围环境的热辐射ΦRad；高温坯料与外部空气产生热对流散热ΦConv。根据能量守恒定律，即QJ=ΦS+ΦCond+ΦRad+ΦConv。电辅助板材V弯模拟及实验选择有效电流密度为3~5 A/mm2，其对应的坯料温度区间在500~900 ℃。
2) 在有效电流密度4 A/mm2下模拟得到坯料在电辅助加热一段时间后中间处温度分布，在厚度和宽度方向各取5个点，结果如图7(b)所示，两端坯料与空气中的热对流的速率较快，使得热损失明显；而中部区域温度较平稳，达到很好的加热条件。在板料的宽度和厚度方向上温度呈正态分布，越靠近中性层温度越高。
3) 在有效电流密度4 A/mm2下模拟得到在电辅助V弯过程中坯料中间变形区(内表面、中心处、外表面)的温度随时间变化结果，如图7(c)所示。内表面因为与模具的持续接触换热，温度降低幅度最大。在成形过程中，坯料弯曲处厚度减薄，导致电阻变大，电阻热变大。但增加的电阻热不足以抵消坯料与模具的换热，从而表现出温度的降低。
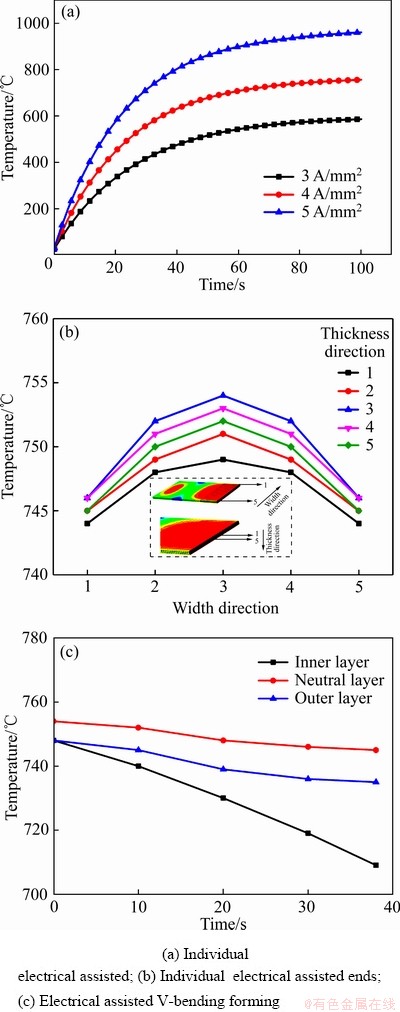
图7 不同阶段温度结果
Fig. 7 Temperature results at different stages
2.3 回弹分析
回弹角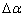
计算如图8所示，
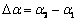。不同弯曲角、相对弯曲半径、有效电流密度、成形速度对回弹角的影响如图9所示。随着弯曲角从60°增加到120°，回弹角度呈上升趋势。在弯曲半径相同时，弯曲角越大，表明变形区弯曲变形的长度越大，则积累的弹性变形总量越大，回弹越大[24]。所以，弯曲角越大，回弹量越大。
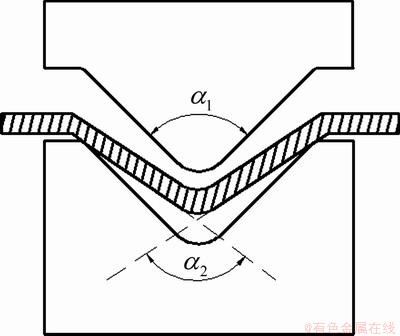
图8 回弹角计算
Fig.8 Calculation of springback angle
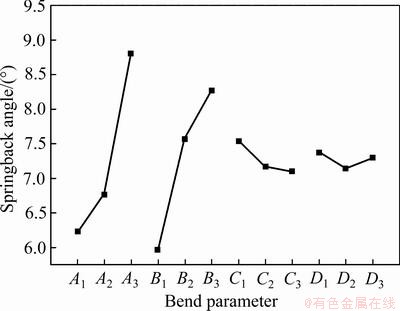
图9 弯曲参数对回弹的影响
Fig. 9 Effects of bending parameters on springback angle
随着相对弯曲半径从2增加到8，回弹角呈上升趋势。这是因为相对弯曲半径越大，其变形程度越小，中性层两侧的纯弹性变形区增加越多，塑性变形区总变形中弹性变形所占的比例同时也增大，这就是很大的工件不易弯曲成形的原因[25]。当凸模圆角半径增加时，侧壁长度变短，冲压深度变短，从而导致侧壁弯曲变形区和变形程度的下降[26]。弯曲半径较大时，坯料的变形程度较小，参与变形的板材区域较大，板材中处于弹性变形的区域占总变形区域的比例较大，当外加载荷卸除后，发生了较大的回弹，最终表现为回弹角的增加[27]。
随着有效电流密度的增加，回弹角略有降低。主要是因为电流密度的增加，导致温度的上升，从而改变了其泊松比、弹性模量，温度的上升，其比值增加，从而引起回弹角的降低[28]。随着成形温度的升高，板材的流变应力减小，会使其弯曲件回弹角减小[29]。
随着成形速度的上升，回弹角先降低后上升。这是因为V弯过程中，成形速度的大小决定弯曲成形时间。板材流变行为受到成形温度与应变速率的双重作用：成形温度的升高及应变速率的降低能使板材流变应力减小。随着成形速度的提高，板料的回弹角开始出现逐渐减小的现象[30]。当板材成形过程中存在板材与模具的传热作用，使成形中板材的温度降到较低温度，而低温时Ti55板材流变行为对成形速度的敏感性较低，此时成形温度对回弹角的影响起主要作用。当板料成形温度超过一定值时，成形速度的大小对弯曲成形过程中板材变形区的温度有较大的影响。当成形速度大于0.5 mm/s时，应变速率对板材的流变应力的影响大于温度的影响，所以成形速度为0.5 mm/s时的回弹角最小。
采用正交试验模拟分析了弯曲角、相对弯曲半径、有效电流密度及成形速度4个因素对Ti55合金板材V弯回弹角影响的主次及显著关系。以板材回弹角的大小作为试验指标来评价各因素对回弹角影响的大小情况。其A代表弯曲角(°)，B代表相对弯曲半径，C代表有效电流密度(A/mm2)，D代表成形速度(mm/s)，每个因素取三个水平，正交试验表及模拟结果如表4所示。
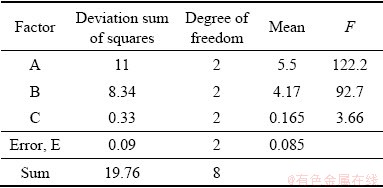
极差分析如表5所示，成形速度对回弹角影响较小，对指标影响不明显，因此将该因素忽略。采用其他3个因素和1个误差列进行3因素3水平的方差分析各因素对回弹角影响的显著性，结果如表6所示。因为 临界值F0.01(2，2)=99，F0.05(2，2)=19，F0.10(2，2)=9，所以可得到弯曲角对回弹角有高度显著影响，相对弯曲半径对回弹角有显著影响，有效电流密度对回弹角没有显著影响。对比极差分析可知，方差分析与极差分析的结论相同。
表4 电辅助V弯模拟正交表及模拟结果
Table 4 Electrical assisted V-bending simulation orthogonal table and simulation results
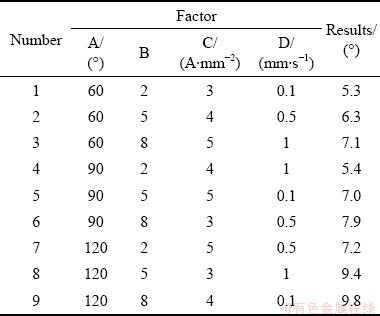
表5 V弯回弹角极差分析表
Table 5 V-bending springback angle range analysis table
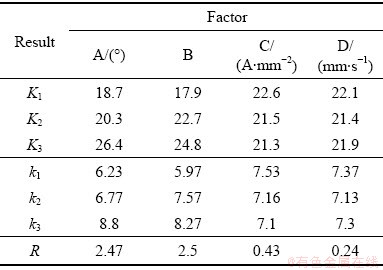
表6 模拟的方差分析表
Table 6 Analysis of variance analysis table
选取相对弯曲半径5，弯曲角90°，成形速度1 mm/s的参数，利用电辅助将坯料加热至机械V弯相近温度后(500 ℃、600 ℃、700 ℃、800 ℃、900 ℃)，模拟电辅助V弯与机械V弯，回弹角结果如图10 所示。机械V弯平均回弹角为13.3°，电辅助V弯回弹角平均6.8°，电辅助V弯比机械V弯回弹角平均降低48.7 %。
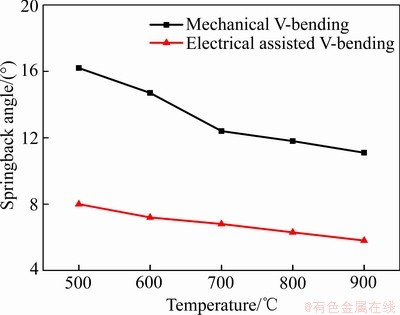
图10 机械V弯与电辅助V弯回弹角
Fig. 10 Springback angle of mechanical V-bending and electrical assisted V-bending
选取上述温度为700 ℃的参数，分析两种条件下Ti55板材V弯前后温度分布，结果如图11所示。从图11(b)中得到，电辅助V弯后的坯料温度机械V弯高200 ℃左右。文献[31]中指出板面高温区域面积越大，回弹量越小，电辅助下高温区域相较更多导致回弹减小。
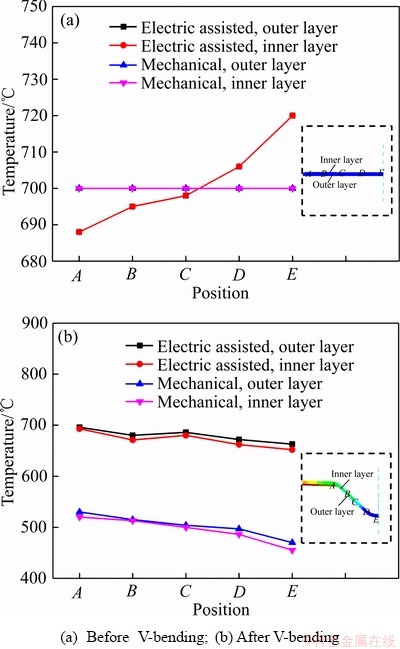
图11 电辅助弯曲及机械弯曲温度分布
Fig. 11 Temperature distribution of electrically-assisted bending and mechanical bending
文献中[32]回弹角的计算公式如下：
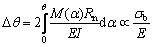(4)
式中：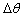
为回弹角；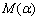
为弯矩；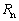
为中性层半径；E为弹性模量；
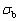为屈服强度；I为惯性矩。
由式(4)得到，回弹角与屈服强度和弹性模量的比值呈正比。低温下钛合金的屈服强度和弹性模量的比值较高，回弹量较大；高温下的屈服强度和弹性模量的比值较低，回弹量较小[33]。故电辅助下回弹较小。
弯曲过程中，应变中性层算公式如下：
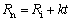(5)
式中：Rn为中性层半径；Ri为弯曲变形区内半径；t为板料初始厚度；k为中性层系数。
式(4)得到弯曲后回弹角与应变中性层有关，电辅助下温度较高，应变中性层半径减小，导致回弹减小。残余应力随着温度的升高而降低，电辅助导致的残余应力松弛也是钛合金高温回弹减少的原因[34]。
从温度分布来看，电辅助加热坯料后，坯料温度分布不均匀，V弯成形前坯料中间处(E处)温度最高，在成形时与模具接触时间最长，成形后温度最低，CE处厚度减薄，在电流大小不变的情况下，CE处有效电流密度增加，由电流导致的温升增加，但越靠近E处与模具的传热越多，综合影响下，C处温度比B、D处温度高，文献[35]中指出这样的温度分布有利于回弹角的减小。
2.4 回弹预测模型
本文采用径向基函数法确定电辅助V弯工艺参数与回弹角的关联关系。在径向基函数模型方 法[34]中，找寻函数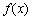
，(
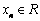) 来近似n 维变量实值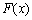函数
；函数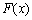用φ (r)作为基函数，φ (r)是由x与每一个数据点xi径向距离r决定的。径向基函数的基本形式[36]如下：
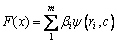(6)
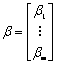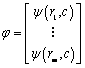式中：
，
，式中：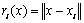
，是 x与第i个采样点xi在设计空间的距离；φ(·)为基函数；‖·‖为欧氏范数，c为非负常数，β为的距离基函数φ(·)的加权系数。径向基近似模型一般可表达如下：
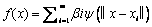(7)
用式(6)作为预测模型时，它满足如下的插值条件：
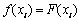(i=1, …, m)
带入得到方程组
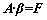(8)
其中，
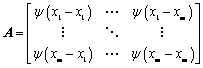向量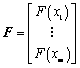
，式(7)在样本点不重合，且函数
为正定函数时存在唯一解，即
(9)
经过对基函数的分析比较，以逆多二次函数为基函数时精度最高，其表达式如下：
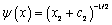(10)
式中：c为非负常数，本次取1。先计算出A，再计算出b；
得到系数矩阵：
b=[2.8733 3.2736 5.0088 2.4545 3.8887 5.5504 3.9808 5.7571 6.9009]-1
由于回弹预测模型是在一定范围内根据数据进行拟合而建立的，故有一定的适用性。此回弹预测模型适用于弯曲角60°~120°、相对弯曲半径2~8、有效电流密度3~5 A/mm2、成形速度0.1~1 mm/s的薄板Ti55合金电辅助弯曲成形中。
2.5 实验验证
在弯曲角90°、相对弯曲半径5、有效电流密度3~4 A/mm2、成形速度0.5~1 mm/s条件下进行了物理工艺实验，具体参数如表7所示，实验后试样如图12所示。
使用游标卡尺测量电辅助V弯实验坯料实验前后厚度，用红外热成像仪每隔5 s记录下坯料温度，用数字量角器测量坯料回弹角大小。
工艺参数1的实验与模拟的坯料厚度、温度对比结果如图13所示，相对误差分别为9.4%和4.6%，验证了有限元模型的可靠性。各工艺参数下回弹角的有限元仿真模拟值、实验值、以及响应函数预测值如表8所示，实验与预测模型的回弹角平均误差为13.4%，验证了回弹预测模型具有较高的准确性。
图12 Ti55合金板材电辅助V弯后试样
Fig. 12 Ti55 alloy sheet after electrical-assisted V-bending
表7 工艺参数
Table 7 Process parameters
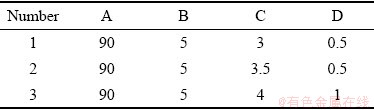
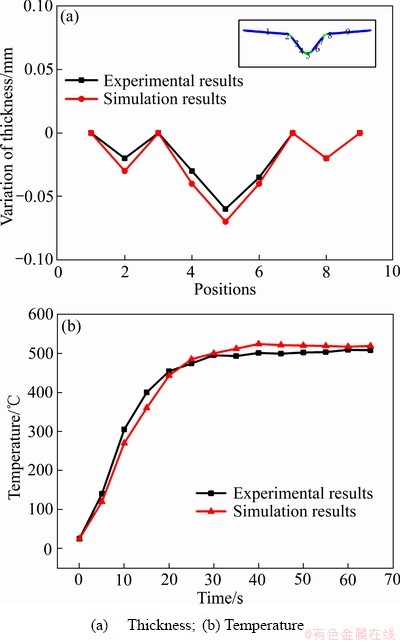
图13 物理实验与有限元模拟结果对比
Fig. 13 Comparison of physical experiment and finite element simulation results model
表8 回弹试验值、仿真模拟值及响应函数预测值
Table 8 Springback test value, simulation value and response function prediction value
3 结论
1) 弯曲角和相对弯曲半径对回弹角有显著影响；有效电流密度和成形速度对回弹角的影响较小。弯曲角为60°~120°、相对弯曲半径为2~8时，弹性变形占比越大，从而回弹量越大；有效电流密度为3~5 A/mm2时，成形温度越高，回弹角越小；随着成形速度从0.1 mm/s增加到1 mm/s，在应变速率和成形温度的共同作用下，回弹角先减小后增大。电辅助板材V弯能有效降低坯料的回弹角，相比机械V弯回弹角平均降低。
2) 利用正交实验方法，以逆多二次函数为基函数，得到系数矩阵，建立了Ti55合金电辅助V弯回弹预测的径向基函数近似模型。
3) 电辅助V弯实验得到坯料厚度、温度变化，与模拟的结果相比，平均相对误差分别为9.4%和4.6%，验证了有限元模型的可靠性；实验和模型预测回弹角的平均误差为13.4%，验证了回弹预测模型的准确性。
REFERENCES
[1] 王鼎春. 高强钛合金的发展与应用[J]. 中国有色金属学报, 2010, 20(S1): 958-963.
WANG Ding-chun. Development and application of high strength titanium alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(S1): 958-963.
[2] 叶建华, 陈明和, 王 宁, 等. 基于修JC模型的TA12钛合金高温流变行为[J]. 中国有色金属学报, 2019, 29(4): 733-741.
YE Jian-hua, CHEN Ming-he, WANG Ning, et al. High temperature rheological behavior of TA12 titanium alloy based on modified JC model[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(4): 733-741.
[3] GAO Peng-fei, YANG He, FAN XIAO-guang. Three-state structure prediction of titanium alloy under isothermal local loading and complex thermal deformation history[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(11): 2423-2433 .
[4] 方 波, 陈志勇, 陈仲强. Ti 55 钛合金连续冷却转变曲线的测绘及显微组织演变[J]. 中国有色金属学报, 2010, 20(S1): s32-s35.
FANG Bo, CHEN Zhi -yong, CHEN Zhong -qiang. Continuous cooling transformation diagram and microstructure evolution of Ti 55 alloy[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(S1): s32-s35.
[5] WANG Li-fei, HUANG Guang-sheng, ZHANG Hua, et al. Evolution of springback and neutral layer of AZ31B magnesium alloy V-bending under warm forming conditions[J]. Journal of Materials Processing Technology, 2013, 213(6): 844-850.
[6] 白雪飘, 王耀奇, 侯红亮. Ti-6Al-4V钛合金热成形极限图及其应用[J]. 塑性工程学报, 2013(3): 102-105.
BAI Xue-piao, WANG Yao-qi, HOU Hong-liang. Ti-6Al-4V titanium alloy hot forming limit diagram and its use[J]. Journal of Plasticity Engineering, 2013(3): 102-105.
[7] MAENO T, TOMOBE M, MORI K, et al. Hot stamping of titanium alloy sheets using partial contact heating[J]. Procedia Manufacturing, 2018, 15: 1149-1155.
[8] GISARIO A, BARLETTA M, VENETTACCI S. Improvements in springback control by external force laser- assisted sheet bending of titanium and aluminum alloys[J]. Optics & Laser Technology, 2016, 86: 46-53.
[9] NIE Da-ming, LU Zhen, ZHANG Kai-feng. Hot bending behavior of SUS 304 stainless steel sheet assisted by resistance heating: Multi-field coupling numerical simulation and experimental investigation[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87(9/12): 2763-2774.
[10] WU HONG-bin, TO S. Effects of electropulsing treatment on material properties and ultra-precision machining of titanium alloy[J]. International Journal of Advanced Manufacturing Technology, 2015, 82(9): 2029-2036.
[11] XIE Huan-yang, WANG Qian, LIU Kai, et al. Investigation of influence of direct-current pulses on springback during V-bending of AZ31B magnesium alloy sheet[J]. Journal of Materials Processing Technology, 2015, 219: 321-327.
[12] 李 超, 李彩霞, 赵 闪. 脉冲电流条件下工业态AZ31镁合金板材的气胀成形[J]. 中国有色金属学报, 2015, 25(3): 553-559.
LI Chao, LI Caixia, ZHAO Shan. Inflatable forming of industrial AZ31 magnesium alloy sheet under pulse current conditions[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(3): 553-559.
[13] ZHAO Yi-xi, PENG Lin-fa, LAI Xin-min. Influence of the electric pulse on springback during stretch U-bending of Ti6Al4V titanium alloy sheets[J]. Journal of Materials Processing Technology, 2018, 261: 12-23.
[14] 官英平, 赵 军. 板材V形自由弯曲智能化控制技术[J]. 机械工人, 2005(12): 9-12.
GUAN Ying-ping, ZHAO Jun. Intelligent control technology of v-shaped free bending for sheet metal[J]. Mechanics, 2005(12): 9-12.
[15] 李金华, 张建李, 姚芳萍. 钛合金板材激光弯曲成形工艺参量分析与弯曲角度预测[J]. 塑性工程学报, 2018, 25(6): 71-75.
LI Jin-hua, ZHANG Jian-li, YAO fang-ping. Process parameters analysis and bending angle prediction of titanium alloy sheet laser bending[J]. Journal of Plastic Engineering, 2008, 25(6): 71-75.
[16] 韩 江, 窦龙龙, 夏 链. 基于径向基函数近似模型的板料自由折弯成形回弹预测[J]. 锻压技术, 2019(6): 30-35.
HAN Jiang, DOU Long-long, XIA Lian. Prediction of springback in free-bending sheet metal forming based on radial basis function approximation model[J]. Forging Technology, 2019(6): 30-35
[17] 穆雪峰. 多学科设计优化代理模型技术的研究和应用[D]. 南京: 南京航空航天大学, 2004: 40-43.
MU Xue-feng. Research and application of agent model technology for multi disciplinary design optimization[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2004: 40-43.
[18] 颜 茜, 舒鑫柱, 祝菲霞, 等. TC11钛合金4种典型组织静态力学性能对比研究[J]. 云南大学学报(自然科学版), 2016, 38(1): 99-104.
YAN Qian, SHU Xin-zhu, ZHU Fei-xia, et al. Comparative study on static mechanical properties of four typical microstructures of TC11 titanium alloy[J]. Journal of Yunnan University(Natural Science Edition), 2016, 38(1): 99-104.
[19] 杨慧丽. TC21钛合金组织与性能的关系[J]. 中国金属通报, 2013(14): 44-45.
YANG Hui-li. The relationship between the structure and properties of TC21 titanium alloy[J]. China Metal Bulletin, 2013(14): 44-45.
[20] 魏寿庸, 贾栓孝, 王鼎春. 550 ℃高温钛合金的性能[J]. 钛工业进展, 2000(2): 25-29.
WEI Shou-yong, JIA Shuan-xiao, WANG Ding-chun. Properties of high temperature titanium alloy at 550 ℃[J]. Progress of Titanium Industry, 2000(2): 25-29.
[21] 丁俊豪, 李 恒, 边天军. 电塑性及电流辅助成形研究动态及展望[J]. 航空学报, 2018, 39(1): 15-32.
DING Jun-hao, LI Heng, BIAN Tian-jun. Research trends and prospects of electroplasticity and current-assisted forming[J]. Acta Aeronautica Sinica, 2018, 39(1): 15-32.
[22] 何 俊, 惠瑞拓, 曾卫东. TC17钛合金加热过程中的有限元模型[J]. 钛工业进展, 2019(2): 8-11.
HE Jun, HUI Rui-tuo, ZENG Wei-dong. Finite element model of TC17 titanium alloy during heating process[J]. Progress of Titanium Industry, 2019(2): 8-11.
[23] 刘 庄, 吴肇基, 吴景之. 热处理过程的数值模拟[M]. 北京: 科学出版社, 1996: 21-24.
LIU Zhuang, WU Zhao-ji, WU Jing-zhi. Numerical simulation of heat treatment process[M]. Beijing: Science Press, 1996: 21-24.
[24] LIU Yong, WANG Liang, ZHU Bin, et al. Identification of two aluminum alloys and springback behaviors in cold bending[J]. Procedia Manufacturing, 2018, 15: 701-708.
[25] 黄新莲. V型弯曲件回弹规律的有限元分析[J]. 模具技术, 2006(4): 7-10.
HUANG Xin-lian. Finite element analysis of the springback law of V-shaped bending parts[J]. Mould Technology, 2006(4): 7-10.
[26] MA Wei-pin, WANG Bao-yu, XIAO Wen-chao, et al. Springback analysis of 6016 aluminum alloy sheet in hot V-shape stamping 6016[J]. Journal of Central South University, 2019, 26(3): 524-535.
[27] 皇 涛, 王 锟, 詹 梅, 等. 考虑材料参数变化的高强钛管数控弯曲回弹行为研究[J]. 精密成形工程, 2019, 11(4): 97-103.
HUANG Tao, WANG Kun, ZHAN Mei, et al. Research on springback behavior of high-strength titanium tubes under numerical control considering the change of material parameters[J]. Precision Forming Engineering, 2019, 11(4): 97-103.
[28] WANG Li-fei, HUANG Guang-sheng, ZHANG Hua, et al. Evolution of springback and neutral layer of AZ31B magnesium alloy V-bending under warm forming conditions[J]. Journal of Materials Processing Technology, 2013, 213(6): 844-850.
[29] MOON Y H, KANG S S, CHO J R. Effect of tool temperature on the reduction of the springback of aluminum sheets[J]. Journal of Materials Processing Technology, 2003, 32(1/3): 365-368.
[30] 贾林玲, 王尚林. 基于Dynaform的V形件成形及弯曲回弹的数值模拟分析[J]. 机械制造, 2016, 54(9): 42-44.
JIA Lin-ling, WANG Shang-lin. Numerical simulation analysis of forming and bending springback of V-shaped parts based on Dynaform[J]. Machinery Manufacturing, 2016, 54(9): 42-44.
[31] 谢 栋, 赵 耀, 董宏宝. 船体中厚钢板局部热压成形中的回弹仿真分析[J]. 中国舰船研究, 2017(5): 132-140.
XIE Dong, ZHAO Yao, DONG Hong-bao. Simulation analysis of springback in local hot press forming of medium-thick steel plate of hull[J]. Chinese Ship Research, 2017(5): 132-140.
[32] AO D, CHU X, YANG Y. Effect of electropulsing on springback during V-bending of Ti-6Al-4V titanium alloy sheet[J]. The International Journal of Advanced Manufacturing Technology, 2018(96): 3197-3207.
[33] 周兆锋, 陈明和, 董小飞. TC4钛合金环热应力校形的数值模拟研究[J]. 新技术新工艺, 2009(12): 67-71.
ZHOU Zhao-feng, CHEN Ming-he, DONG Xiao-fei. Numerical simulation study on thermal stress shaping of TC4 titanium alloy ring[J]. New Technology and New Process, 2009(12): 67-71.
[34] 刘 坡, 宗影影, 郭 斌. 钛合金高温短时蠕变与应力松弛的关系研究[J]. 材料研究学报, 2014, 28(5): 339-345.
LIU Po, ZONG Ying-ying, GUO Bin. Study on the relationship between high temperature short-time creep and stress relaxation of titanium alloys[J]. Chinese Journal of Materials Research, 2014, 28(5): 339-345.
[35] NIE Da-ming, LU Zhen, ZHANG Kai-feng. Hot V-bending behavior of pre-deformed pure titanium sheet assisted by electrical heating[J]. The International Journal of Advanced Manufacturing Technology, 2018, 94: 163-174.
[36] 吴宗敏. 径向基函数、散乱数据拟合与无网格偏微分方程数值解[J]. 工程数学学报, 2002, 19(2): 1-12.
WU Zong-min. Radial basis function, scattered data fitting and numerical solution of meshless partial differential equations[J]. Journal of Engineering Mathematics, 2002, 19(2): 1-12.
Electric-thermal-mechanical coupled simulation and springback prediction of Ti55 alloy electrical assisted V-bending
LI Ping, XIE Xiu-ming, WANG Hui-gan, YAN Si-liang, XUE Ke-min
(School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract: In order to study the springback law of Ti55 alloy sheet by electrical assisted V-bending, a three-dimensional electric-thermal-mechanical coupled finite element model of electrical assisted V-bending of Ti55 alloy sheet is established based on the ABAQUS software. Orthogonal test simulation was carried out on the V-bending and springback process, the influence of bending angle, relative bending radius, effective current density, forming speed was studied, and a springback prediction model based on radial basis function was established. The results show that: within the range of selected parameters, as the bending angle and the relative bending radius increase, the springback angle increases. The springback angle decreases with the increasing of effective current density. As the bending velocity increases, the springback angle decreases first and then increases. Range analysis and analysis of variance show the bending angle and the relative bending radius have a significant effect on the springback angle. Compared with the mechanical V-bending, electrical assisted V-bending reduces the springback angle by 48.7% on average. Conducted an electrical assisted V-bending experiment, comparing the thickness, temperature change and springback angle, the average errors were 9.4%, 4.6% and 13.4%, which verified the accuracy of the finite element simulation and springback prediction model.
Key words: titanium alloy; electrical assist; springback prediction; finite element simulation
Foundation item: Project(61409230408) supported by the Weapons and Equipment Pre-Research Field Fund of China; Project(2017ZEP4003) supported by Aeronautical Science Foundation of China; Project (201901SY008601) supported by The Open Project of the National Key Laboratory for Precision Hot Forming of Metals
Received date: 2020-04-24; Accepted date: 2020-07-31
Corresponding author: XUE Ke-min; Tel: +86-13865927005; E-mail: xuekm@hfut.edu.cn
(编辑 何学锋)
基金项目：装备预研领域基金资助项目(61409230408)；航空科学基金资助项目(2017ZEP4003)；金属精密热加工国防科技重点实验室开放基金资助项目(201901SY008601)
收稿日期：2020-04-24；修订日期：2020-07-31
通信作者：薛克敏，教授，博士；电话：13865927005；E-mail：xuekm@hfut.edu.cn
