一种前轮驱动自行车机器人的非完整约束
黄用华,廖启征,魏世民,郭磊
(北京邮电大学 自动化学院,北京,100876)
摘要:提出递推计算1种前轮驱动自行车机器人系统非完整速度约束的方法,并进行物理样机实验验证。引入随动和半随动坐标系描述系统运动,并利用刚体间的相对运动关系推导出该自行车机器人各刚体运动参数,结合车轮纯滚动条件建立了其递推形式非完整速度约束方程。综合安装在车架上的惯性测量单元以及安装在前后轮、车把上的光电编码器的实测信息,利用1台实物自行车机器人样机对所建立的非完整运动约束方程进行实验验证。结果表明:自行车机器人系统只有车架的横滚角速度、车把的转动角速度以及前轮的驱动角速度3个独立速度,车架航向角速度和后轮相对车架的转动速度是这3个独立速度的函数;传感器测量结果与非完整运动约束方程数值计算结果吻合,验证所建立的非完整运动约束方程是可信的。
关键词:自行车机器人;非完整约束;前轮驱动;惯性测量单元;编码器
中图分类号:TP24 文献标志码:A 文章编号:1672-7207(2011)S1-0512-07
Nonholonomic constraints of a bicycle robot with front-wheel drive
HUANG Yong-hua, LIAO Qi-zheng, WEI Shi-min, GUO Lei
(School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China)
Abstract: A recursion computing method with nonholonomic constraints of a front-wheel driven bicycle robot was proposed and validation experiments were carried out on a physical prototype. Follow-up coordinate system and partly follow-up coordinate system were adopted to describe the movement of the robot. Movement parameters were derived according to the principle of relative motion between adjacent bodies and recursion form constraint equations were deduced based on the assumption of rolling without slipping of wheels. Combining measuring information of inertial measurement unit on the frame and encoders on joints, experiment was carried out on a real robot. The results show that, there are only three independent speeds in the system, which are the rolling speed of the frame, the rotational speed of the front-fork and the rotational speed of the front wheel, and yaw angle rotational speed of the front-fork and rotational speed of rear wheel are both the function of the three independent speeds. The experimental data are consistent with the theoretical analysis results from the derived equations, which validate the proposal nonholonomic constraints accordingly.
Key words: bicycle robot; nonholonomic constraints; front-wheel drive; inertial measurement unit; encoder
双轮自行车机器人是1种具有欠驱动和非完整约束特性的全方位移动机器人,因其拥有体积小、机动灵活、能源利用率高、转弯半径小等优点而受到广泛的关注。国内外有许多学者针对该类机器人的调整机构设计、动力学建模、稳定平衡控制和轨迹跟踪等问题进行了研究[1-7],其中作为平衡控制前提的动力学建模研究得最多,几乎所有的文献都有所涉及。双轮自行车机器人是静态不稳定,动态可稳定的系统,首要解决的是车体的稳定平衡问题,这点与3个或4个轮子的轮式车不同,后者直接对车体进行路径规划控制即可。基于此,双轮自行车机器人的运动学、动力学模型及运动控制都与三轮或四轮的轮式车有本质的区别。动力学建模是研究自行车机器人稳定平衡控制和轨迹跟踪控制的前提,而自行车机器人的非完整运动约束分析又是动力学建模的基础,它对自行车机器人的控制尤其是轨迹跟踪控制具有重要意义,需要对其进行深入探索。
在已有的自行车机器人研究中,在进行运动分析 时,研究人员通常会引入各种近似来简化模型,比如小角度假设、接地点在车把轴线延长线上等等,这些近似处理一方面降低了模型的精度,在极端情况下甚至会使模型偏离其真实工况;另一方面则容易掩盖自行车系统的内在约束关系,增加控制器设计的难度。此外,目前研究的自行车机器人基本是针对后轮驱动的,对前轮驱动自行车机器人还少有涉及。前轮驱动自行车机器人具有与后轮驱动自行车机器人不同的特点,如零转弯半径、零前进速度下定车等。因此,其模型较之后者会有所不同,特别是系统的运动约束关系会有很大改变,有必要对其进行研究。非完整运动约束分析是自行车机器人动力学建模和运动控制的基础,又是一个容易被忽视的问题。本文作者引入随动坐标系和半随动坐标系,从精确的运动学分析出发,建立并采用实物样机实验验证1种前轮驱动自行车机器人受到的非完整运动约束。
1 物理样机
图1所示为前轮驱动的自行车机器人样机。系统主要由前轮、后轮、车架、车把4部分组成。其中:车架上分别安装有电池组、控制板、惯性测量单元等装置;2个驱动电机(1个步进电机和1个直流无刷电机)分别安装在车把和前轮的对应关节处,通过齿轮减速器驱动车把和前轮。

图1 自行车机器人物理样机
Fig.1 Prototype of bicycle robot
2 非完整约束
2.1 拓扑结构
引入拓扑来描述多体机械系统各个构件之间的关系,以便对系统进行运动学分析。
将多体系统中的构件定义为物体,物体间的运动约束定义为铰链接就可以得到系统的拓扑。
记地球为刚体 ,车架为
,车架为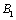 ,后轮为
,后轮为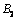 ,车把为
,车把为 ,前轮为
,前轮为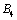 ,根据图1所示的样机得出自行车机器人的拓扑构型如图2所示。
,根据图1所示的样机得出自行车机器人的拓扑构型如图2所示。

图2 自行车机器人的拓扑结构
Fig.2 Topological structure of bicycle robot
在图2中,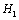 和
和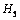 为五类副,其余
为五类副,其余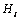
 均为一类副并且都为转动副。加黑的箭头表示该处为有电机驱动,箭头方向指明2个邻接刚体中箭头指向的刚体相对箭头背离的刚体运动。
均为一类副并且都为转动副。加黑的箭头表示该处为有电机驱动,箭头方向指明2个邻接刚体中箭头指向的刚体相对箭头背离的刚体运动。
2.2 坐标系
假设自行车机器人在水平面上运动,且车轮与地面无相对滑动,建立如图3所示的坐标系统。
(1) 坐标系e为惯性参考坐标系;

图3 自行车机器人坐标系示意图
Fig.3 Schematic of bicycle robot
(2) 坐标系e(1)与车架固连,原点在后轮中心;
(3) 坐标系e(2)与后轮部分固连,为半随动坐标系,其 始终平行地面,原点与e(1)系的重合;
始终平行地面,原点与e(1)系的重合;
(4) 坐标系e(3)与车把固连,原点在车架与车把转动轴线的交点;
(5) 坐标系e(4)与前轮部分固连,也是半随动坐标系,原点在前轮的几何中心;
(6) 初始时刻坐标系e,e(1),e(2)以及e(4)方向一致,而坐标系e(3)则绕e2轴转过α角。
2.3 运动参数
定义车架的3个欧拉角ψ,θ和φ分别为广义坐标q1,q2和q3,后轮相对车架的转角为q4,车把相对车架的转角为q5,前轮相对车把的转角为q6,则车架的角速度为:
 (1)
(1)
其中:R为旋转变换矩阵。将上式展开整理得到:

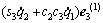 (2)
(2)
式中:si和ci分别表示sinqi和cosqi (i=1, 2, 3)。
定义新变量:
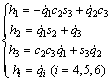 (3)
(3)
则车架的角速度可以改写为:
 (4)
(4)
设ξ为坐标系e(1)与坐标系e(2)的夹角,则坐标系e到坐标系e(2)的变换矩阵可表示为:
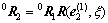 (5)
(5)
式中:矩阵 。因为坐标轴
。因为坐标轴 始终与地面平行,所以,令
始终与地面平行,所以,令
 (6)
(6)
式中: 为坐标轴e1的单位矢量,且
为坐标轴e1的单位矢量,且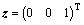 。通过式(6)可以确定ξ的表达式。
。通过式(6)可以确定ξ的表达式。
由于后轮相对车架转动,因此,后轮角速度 为:
为:
 (7)
(7)
将 向坐标系e(2)投影可以得到:
向坐标系e(2)投影可以得到:

 (8)
(8)
其中: ;
;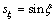 。
。
同理,由车把角速度 可以得到:
可以得到:

 (9)
(9)
其中:s5和c5分别表示sinq5和cosq5。
设η为坐标系e(3)与坐标系e(4)的夹角,则坐标系e到坐标系e(4)的变换矩阵可表示为:
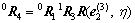 (10)
(10)
式中:矩阵 。
。
与坐标系e(2)类似,因为 始终与地面平行,所以,令
始终与地面平行,所以,令
 (11)
(11)
可以确定η的表达式。
根据前轮角速度 ,有:
,有:

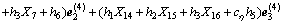 (12)
(12)
其中:cη表示cosη。
这里,Xi(i=10, ··· , 16)是为了避免重复计算而引入的中间变量,它们是各关节转角的复变函数,后面的Xi(i≥17)也有类似的定义。
设前车轮接地点PB的矢径 ,其中r1为前车轮半径。由于前轮与地面无相对滑动,因此其接地点PB的速度vB满足约束方程:
,其中r1为前车轮半径。由于前轮与地面无相对滑动,因此其接地点PB的速度vB满足约束方程:
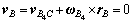 (13)
(13)
式中: 为前轮质心的线速度。于是有:
为前轮质心的线速度。于是有:
 (14)
(14)
将 向坐标系e(3)投影,经整理得:
向坐标系e(3)投影,经整理得:
 (15)
(15)
记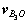 为坐标系e(3)原点的速度,根据同一刚体上2点的运动关系,有
为坐标系e(3)原点的速度,根据同一刚体上2点的运动关系,有
 (16)
(16)
式中: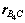 为前轮质心的矢径,且
为前轮质心的矢径,且 (如图3所示)。类似地,可求
(如图3所示)。类似地,可求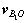 的表达式。
的表达式。
由于 ,后轮接地点PA的矢径
,后轮接地点PA的矢径 ,所以,PA点的速度为
,所以,PA点的速度为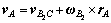 ,在e(2)系表示为:
,在e(2)系表示为:
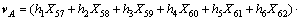
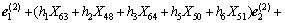
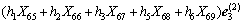 (17)
(17)
2.4 非完整运动约束
完整约束是指约束方程中不含确定系统位置的坐标的微商,或含有坐标的微商但不利用动力学方程就可直接积分成为不含坐标微商的约束。而非完整约束则是指系统约束方程中含有确定系统位置坐标的微商且不利用动力学方程不能直接积分为不含坐标微商的约束。下面就基于上述定义展开自行车机器人所受约束的分析。
前轮接地点PB和后轮接地点PA的齐次坐标为:
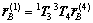 ,
,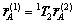 (18)
(18)
其中,齐次变换矩阵为:
 ;
; ;
; ;
;
齐次坐标为:
 ;
; ;
;
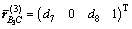 ;
; 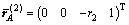 。
。
根据式(18)可以求出矢量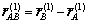 。坐标轴e1的单位矢量在坐标系e(1)的描述为
。坐标轴e1的单位矢量在坐标系e(1)的描述为 。其中:
。其中: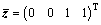 。由于矢量
。由于矢量 在水平面上,因此,矢量点积为:
在水平面上,因此,矢量点积为:
 (19)
(19)
式(19)为系统受到的完整约束,它描述的是车架俯仰角和车把转角的约束关系。
相对而言,非完整约束对自行车机器人的稳定平衡控制以及轨迹规划跟踪更有意义。下面推导系统的非完整约束。
考虑到后轮与地面也无相对滑动,其接地点PA的绝对速度也为0。因此,在式(17)中,令速度vA=0,并对其求解hi(i=1, 3, 4),引入新变量后有:
 (20)
(20)
式中: ;
;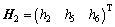 ;X为1个与Xi(i=57, ··· , 69)有关的3×3矩阵。
;X为1个与Xi(i=57, ··· , 69)有关的3×3矩阵。
联合式(20)和式(3),求解 和
和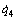 ,得到:
,得到:
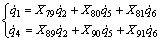 (21)
(21)
式中:系数Xi(i=79, ···, 91)是车架横滚角和车把转角的复变函数。
式(21)即为自行车机器人的非完整速度约束方程,该方程表明:
(1) 系统只有车架的横滚角速度、车把的转动角速度以及前轮的驱动角速度3个独立速度。
(2) 系数Xi(i=79, ···, 91)不含前轮转角、后轮转 角、车架航向角、车架俯仰角变量,即车架的航向角速度、后轮的相对角速度与前轮、后轮、车架航向和俯仰的转角无关。
(3) 系统有3个独立速度,但只有2个有驱动(分别为前轮和车把),因此,其为欠驱动系统。
3 非完整约束验证实验
3.1 自行车机器人系统硬件
系统硬件构成:1块TMS320F28335数字信号处理器(DSP)核心控制板,1块TMS320F2812处理器数据采集卡以及1个C8051F020微处理器电机控制器;2只E6A2-CW5C增量式编码器,1只E6C3-AG5C绝对式编码器,2个ACS713电流传感器和1个MTi航姿惯性测量单元;1对多信道无线数传模块;1台34HS300DZ两相步进电机和1台TDR11Q薄饼式有刷直流电机。系统硬件的结构框图如图4所示。

图4 自行车机器人系统硬件构架
Fig.4 Hardware frame of bicycle robot system
系统各硬件模块功能划分:TMS320F28335负责自行车机器人系统稳定平衡、轨迹规划和路径跟踪等控制算法计算,并与上位机进行通讯,包括上传系统状态和控制数据,解析上位机的控制指令,它是整个机器人硬件控制系统的核心,系统的时序节律由其同步;TMS320F2812完成系统状态数据采集及处理,并将数据实时上传至TMS320F28335;C8051F020负责电机的闭环控制;增量式编码器1和2分别用于测量前轮相对车把的转动速度和后轮相对车架的转动速度;绝对式编码器3用来测量车把转动角度;2个电流传感器分别测量步进电机和直流电机的电流;惯性测量单元用来反馈车架的欧拉角和角速率;超声波传感器阵列用来探测工况环境障碍物。
3.2 实验及结果分析
实验中用到的相关结构参数如表1所示,其中每项的物理含义见图3。
实验开始时,驱动前轮及车把使自行车机器人在水平地面上运动,并保证车轮与地面无滑动,通过传感器采集各相关数据并由无线模块传送到上位PC机。整个实验过程持续16 s,传感器数据采样频率设定为10 Hz,采样数据容量为160组数据。
表1 自行车机器人的部分结构参数
Table 1 Structural parameters of bicycle robot

通过串口交互方式读取MTi惯性测量单元得到车架的3个欧拉角。考虑到惯性测量单元输出角度值是描述在惯性参考坐标系,与建模时假设欧拉角是描述在车架随动坐标系下略有不同,通过式(22)的矩阵方程,可求解ψ,θ和φ得到所要求的数据。

 (22)
(22)
式中:ψs,θs和φs为惯性测量单元输出的3个欧拉角。
图5所示为车架欧拉角与车把转角。其中:qis(i= 1, 2, 3)为实验测量值转换到随动坐标系下的欧拉角。车架的欧拉角速率根据以下中间差分公式进行计算:
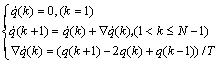 (23)
(23)

图5 测量得到的车架欧拉角qis(i=1, 2, 3)及车把转角q5s
Fig.5 Measured Euler angles qis(i=1, 2, 3) of frame and rotation angle q5s of front-fork
车把转角q5由单圈的绝对编码器采集得到。由于绝对编码器与车把间通过1对3:1减速比的齿轮连接,因此,车把的摆动幅度不能超过1.46 rad(即60°),否则绝对编码器测量值会因为多值而失效,同时还需将采集到的角度值除以减速比才能得到车把的转角。图5中的q5s为测量得到的车把转角。前轮的驱动角速率 以及后轮的转动角速率
以及后轮的转动角速率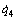 通过脉宽测量由增量编码器采集。
通过脉宽测量由增量编码器采集。
结合速度差分公式(23)得到车把转动角速率 、车架航向角速率
、车架航向角速率 以及车架横滚角速率
以及车架横滚角速率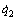 。将前轮的驱动角速率、车把转动角速率、车架横滚角速率以及相关的角度数据代入式(21),计算得到车架航向角速率及后轮转动角速率。
。将前轮的驱动角速率、车把转动角速率、车架横滚角速率以及相关的角度数据代入式(21),计算得到车架航向角速率及后轮转动角速率。
图6和图7所示分别为实验测量值(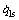 和
和 )与非完整约束计算值(
)与非完整约束计算值(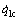 和
和 )的比较曲线。由图6和图7可以看出:除少数几个点外,测量值与非完整约束计算值无论数值还是变化趋势都基本一致。
)的比较曲线。由图6和图7可以看出:除少数几个点外,测量值与非完整约束计算值无论数值还是变化趋势都基本一致。
进一步比较非完整约束计算得到的车架航向角速率及后轮转动角速率与传感器测量值之间的误差,得到如图8所示的误差曲线。表2所示为误差曲线的量化数据分析,包括绝对误差Emax、相对误差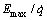 、绝对平均误差Emean以及相对平均误差
、绝对平均误差Emean以及相对平均误差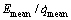 。
。

图6 实验测量值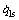 和非完整约束计算值
和非完整约束计算值
Fig.6 Measured values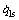 and calculated values
and calculated values

图7 实验测量值 和非完整约束计算值
和非完整约束计算值
Fig.7 Measured values and calculated values
and calculated values

图8 实验数据与数值计算结果误差曲线
Fig.8 Errors between measured and calculated values
如表2所示,后轮转动角速率的绝对误差比航向角的绝对误差大1个数量级,但由于后轮转动角速率较大,基本上都在2 rad/s以上,其相对误差比后者小很多;航向角的相对误差较大,最大值达到409.95%。考虑到航向角速率的平均值为0.066 8 rad/s,而MTi惯性测量单元的航向角输出有0.087 5 rad(即5°)的绝对误差限,故相对误差最大值会出现突变。但由于误差大的点不多,不超过采样总点数的5%,其相对平均误差不大,只有6.44%,因此,相对误差大的点可以看成是传感器测量误差造成的奇异点。
表2 测量值与计算值误差分析
Table 2 Errors analysis between measured and calculated values

可见:除了传感器自身测量误差造成的少数几个奇异点外,实验测量值与非完整约束计算值基本吻合,这在一定程度上验证了所推导的非完整约束方程是可信的。
4 结论
(1) 建立了1种递推形式的前轮驱动自行车机器人非完整约束方程。该非完整约束方程包含3个独立速度,分别为车架的横滚角速度、车把相对车架的转动角速度和前轮的驱动角速度;系统具有2个非完整速度约束,车架航向角速度和后轮相对车架的转动速度是其他3个独立速度的函数。
(2) 物理样机实验验证了所建立的非完整约束方程是可信的。建立的非完整约束方程能够准确地描述前轮驱动自行车机器人内在的约束关系,为自行车机器人动力学建模、稳定平衡及轨迹跟踪控制奠定了 基础。
参考文献:
[1] Tanaka Y, Murakami T. Self sustaining bicycle robot with steering controller[C]// The 8th IEEE International Workshop on Advanced Motion Control, AMC'04. Kawasaki, 2004: 193-197.
[2] Sharma H D, Umashankar N. A robotic model (ROBI) of autonomous bicycle system[C]// Proceedings of IEEE International Conference on Computational Intelligence for Modeling Control and Automation, and International Conference on Intelligent Agents, Web Technologies and Internet Commerce. Sydney, 2006: 107-112.
[3] Astrom K J, Klein R E, Lennartsson A, et al. Bicycle dynamics and control: adapted bicycles for education and research[J]. Control Systems Magazine, IEEE, 2005, 25(4): 26-47.
[4] Yavin Y. The derivation of a kinematic model from the dynamic model of the motion of a riderless bicycle[J]. Computers and Mathematics with Applications, 2006, 51: 865-878.
[5] Yamakita M, Utano A. Automatic control of bicycles with a balancer[C]// Proceedings of the 2005 IEEE International Conference on Advanced Intelligent Mechatronics. Monterey, 2005: 1245-1250.
[6] 郭磊, 廖启征, 魏世民. 自行车机器人动力学建模与MIMO反馈线性化[J]. 北京邮电大学学报, 2007, 30(1): 80-84.
GUO Lei, LIAO Qi-zheng, WEI Shi-min. Dynamic modeling of bicycle robot and nonlinear control based on feedback linearization of MIMO systems[J]. Journal of Beijing University of Posts and Telecommunications, 2007, 30(1): 80-84.
[7] LIU Yan-bin, JIA Chen-hui, HAN Jian-hai. Dynamics modeling of an unmanned bicycle with parallel mechanism adjusting stability[C]// Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation. Changchun, 2009: 1601-1605.
(编辑 何运斌)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家自然科学基金资助项目(50875027、50705010、51075039);北京市自然科学基金资助项目(3053017、3082014、3092015)
通信作者:黄用华(1977-),男,广西梧州人,博士研究生,从事机器人动力学建模与控制研究;电话:010-62282159;E-mail: huangyonghuaxj@sina.com