J. Cent. South Univ. Technol. (2008) 15: 418-422

DOI: 10.1007/s11771-008-0078-8

Dynamic behavior of reinforced concrete frame structure during construction

TIAN Ming-ge(田明革)^{1, 2}, YI Wei-jian(易伟建)¹

(1. College of Civil Engineering, Hunan University, Changsha 410082, China;

2. Construction Engineering Quality Safety Supervision Management Head Station of Hunan Province,

Changsha 410011, China)

Abstract: The effects of concrete’s time-variant elastic modulus, casting structural components, assembling temporary shoring framework system, and shock by operating construction equipment on dynamic behavior of the reinforced concrete frame structure during construction were investigated. The dynamic tests of an eight-storey reinforced concrete frame structure during full-scaled stages of the sixth storey construction cycle were carried out by ambient vibration. Natural frequencies, corresponding mode shapes and damping ratio were determined by power spectrum processing the tested signal data in frequency domain. The changes of frequencies, mode shapes and damping ratios at different construction stages were given. The results show that natural frequencies and modal damping ratios reach the maximum at stage of casting fresh concrete, especially for higher modes. Modal damping ratios at each construction stage are less than 5% of those during usage.

Key words: structural dynamics; ambient vibration; structure during construction; mode shape; natural frequency; modal damping ratio

1 Introduction

Dynamic behavior of the reinforced concrete frame structures is very important to analyze the vibration of structures under wind loads or earthquake loads. According to time-dependent characteristics of concrete, construction series, and action of temporary shoring framework systems, the reinforced concrete structures during construction are time-variant structural systems, and their dynamic behavior is different from that during usage. MEYYAPPA et al^[1] estimated modal parameters of a high-rise building during construction using ambient vibration response data in 1980. SCHUSTER et al^[2] studied the dynamic behavior of a 32-storey high-rise building during construction based on its ambient vibration in 1994. MEMARI et al^[3] tested the dynamic behavior  of a steel frame building during construction based on both ambient and simple harmonic forced vibration to analyze the effect of autoclaved cellular concrete block filler walls on the dynamic behavior in 1999. The analogous work on timber framed building was carried out by ELLIS and BOUGARD in 2001^[4].

In this work, the dynamic behavior of the reinforced concrete frame structures during construction, such as the natural frequencies, the corresponding mode shapes the and damping ratios at each construction stage was studied by testing data on ambient vibration, and compared with that during usage.

2 Description of structure

The structure in this work is an eight-storey reinforced concrete(RC) frame structure built to serve as dormitory, which is uniform in plan and elevation and a representative of the type of current construction. The plan dimensions are 16.80 m×25.20 m, as shown in Fig.1. The structural height is 25.80 m from the foundation, or 24.30 m from the ground level. The height of the first storey is 3.30 m, and those from the second to the eighth storey are 3.00 m. The concrete strength grades of columns are C40 from the 1st to the fourth storey and C35 from the fifth to the eighth storey. The crossed areas of RC columns are 400 mm×500 mm at the first storey, descending with the increase of storey and 300 mm×400 mm at the eighth storey. The floor system consists of casting RC slabs, whose thickness is 120 mm, and the concrete strength grades of all the slabs and beams are C30.

The structure’s construction series are 9 d for con- structing the first storey, and 7 d for other storeys. Three-storey shore framework system consisted of wood shores and bamboo compregs were used. The basic procedures were performed in the same construction cycle including the following operations: 1) setting up a storey of shores; 2) colligating rebar grids; 3) casting the fresh concrete; 4) curing concrete components; 5) removing the forms and shores at the lowest interconnected level, and transmitting forms and shores to the next storey.

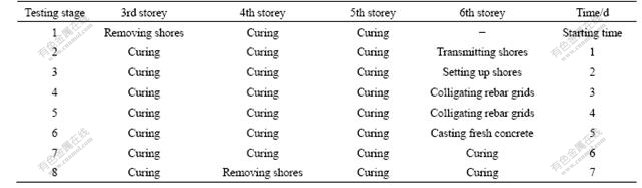
The dynamic testing was carried out during the sixth storey full-scale construction cycle which is divided into eight stages. The interconnected storey and time are shown in Table 1. Time interval was (24±3) h. The ambient vibration response data of each testing stage were respectively recorded to estimate the dynamic behavior.

3 Ambient vibration tests and analysis

The objective of ambient vibration tests is to study the dynamic behavior of a reinforced concrete frame structure during construction. Hence, the tests were carried out in order to estimate the modal frequencies, shapes and damping ratios by measuring ambient vibration. An accelerometer was placed at medium point of axis K on each storey, measuring acceleration along with axis R that is NS direct.

As past experiences of structural dynamics during both construction^[1-4] and usage^[5-8] with the ambient vibration testing procedure have shown its validity, the test has become a practical way to obtain the charac- teristics of structures. Moreover, because the test setup does not require to shut down the structure construction operations, normal operations can go on when testing is carried out. The response of a structure to ambient excitation (micro-tremor, wind, and traffic) mostly tends to vibrate on verge of its natural modes. Hence, it is easy to determine the dominant frequencies by Fourier transformation. Because ambient vibrations normally take place at very low amplitudes, very sensitive instruments are necessary. In this test, the testing system consisted of accelerometers, signal amplifier and data recorder, by which ambient vibration of each storey is synchronously acquired and recorded. The system’s acceleration resolution is 1×10^-5 m/s², and bandwidth is

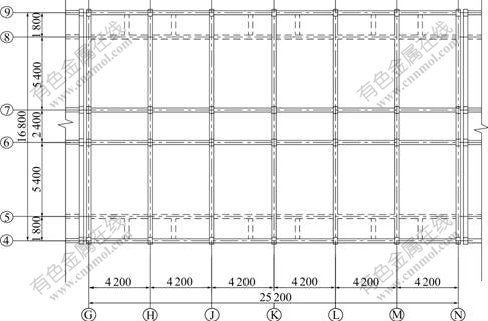
Fig.1 Plan drawing of reinforced concrete frame structure (unit: mm)

Table 1 Operation procedures of eight testing stages

1-30 Hz. Each recorder collected data from all channels simultaneously at a rate of 256 sample/s.

Ideally, when a structure is subjected to excitation by ambient vibration, its response will be the strongest near the resonant frequencies. Resonance appears as peaks on the Fourier spectral curve obtained from response records^[9]. Moreover, for lightly damped structures, with real modes of vibration, these peaks correspond to the damped natural frequencies of the structure. In the analysis of ambient vibration, the following two principal assumptions are applied.

1) The excitation is sufficiently broad band stochastic to excite at least the lowest 3 to 4 modes of the structure.

2) The resonant modes are lightly damped and the resonant frequencies are distinct and well separated.

Under these assumptions, frequencies at maximum spectral amplitudes can be interpreted as the structural resonance frequencies.

The signal data recorded include the direct current useless for estimating dynamic behavior^[10]. Therefore, the direct current part of signal is removed as follows:

                                     (1)

where  x(n) is the original ambient vibration signal; 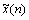 is the signal after removing direct current part; x_m(n) is the statistic mean value of the original signal.

It is expedient that the ambient vibration of structure can be acquired. However, the ambient vibrations analyzed are so low amplitude that the recorded data are interfered by useless noise^[11]. Therefore, it is difficult to analyze ambient vibrations only by conventional spectral analysis techniques. The average spectrum will be calculated as following.

Firstly, the data are divided into some segments based on time sequence, and adjacent segments are overlapped each other. Divide signal 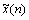 as follows:

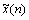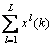→                            (2)

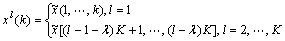(3)

where  x^l(k) is the lth signal sequence segment, k=1, …, K; K is the sample number of every signal sequence segment, l=1, …, L; L is the number of segment; λ is the overlapping coefficient.

Secondly, during calculation by using short Fourier transformation, Hamming windows function is used to mitigate the effect of frequency leak as follows:

               (4)

where H( ) is the Hamming windows function, k=0, 1, …, N-1.

Finally, the average spectrum is calculated to minimally diminish spurious oscillations and maximally enhance time invariant oscillations.

The damping ratio can be estimated from the spectral peak which corresponds to the modal frequency using half-power bandwidth method^[9]:

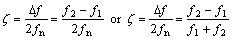        (5)

where  f_n is the frequency of resonant modes; f₁ and f₂ are the frequencies corresponding to the amplitude at half height of the peak spectral amplitude and frequency of f_n. The cubic spline interpolation is used to estimate the approximations of f₁ and f₂, in order to overcome calculation difficulty of discrete spectrum data and enhance the precision of damping ratio.

Based on the acceleration responses at different stories and their phase differences obtained by the fast Fourier transformation^[12], mode shapes could be obtained from the ratios of the cross power spectral amplitudes at resonant frequencies between ambient vibration of the foundation and the stoerys to the self- power spectral amplitude of the foundation vibration of the foundation^[13].

In order to overcome the practical problems, the following steps were applied.

Step 1: Remove direct current part of signal.

Step 2: Calculate the average spectrum.

Step 3: Based on the average spectrum, the modal (resonant) frequencies are identified by comparison of local peculiarities of the structure and incorporating engineering logic and experience.

Step 4: Estimate the modal damping ratios.

Step 5: Estimate the modal shapes.

In this test, the signal processing parameters are shown in Table 2.

Table 2 Signal processing parameters

4 Dynamic behavior of structure during construction

Ambient vibration tests were carried out in eight stages. Calibration of the accelerometers was done at all stages by placing all of them at one location on the stories and foundation. The main objective of the testing was to determine the effect of construction operation on dynamic behavior of the building. The Fourier spectral analysis for the ambient vibration was carried out, and the self-power spectrum(SPS) of foundation motion and the cross power spectrum(CPS) between foundation motion and each storey’s vibration during eight constructional stages were calculated. The results are shown in Fig.2 for the first constructional stage, Fig.3 for the sixth stage, and Fig.4 for the eighth stage, which reveal respectively the frequency domain characteristics about removing shores on the third storey, casting fresh concrete components of the sixth storey, and removing shores on the fourth storey. The foundational modal frequencies, damping ratios, and mode shapes at eighth constructional stages are respectively shown in Figs.5, 6 and 7.

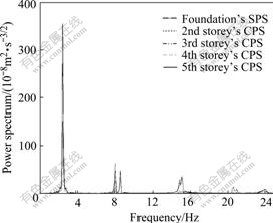
Fig.2 Power spectra of the first stage

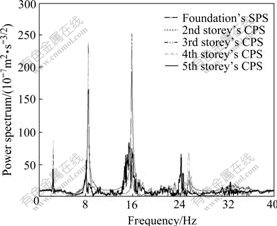
Fig.3 Power spectra of the 6th stage

As shown in Figs.2-7, with the increase of curing time, the structural stiffness increases. At the same time, transmitting shores and colligating rebar grids increase local mass. The above increasing rates influence the dynamic behavior: the foundational modal frequency increasing from the first to the second constructional stage, decreasing from the third to fifth stage, moreover damping ratio decreasing from the first stage to fifth stage.

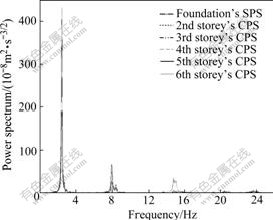
Fig.4 Power spectra of the 8th stage

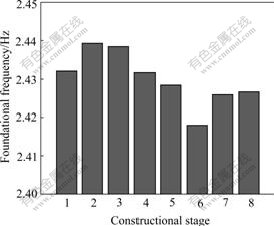
Fig.5 Foundational modal frequencies at different construc- tional stages

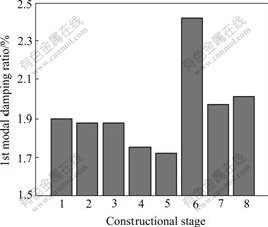
Fig.6 Foundational modal damping ratios at different construc- tional stages

It is clear of the most effect of casting fresh concrete components and the shock of operating construction equipments on dynamic behavior of building during construction. In the construction cycle, fresh concrete contributing only mass but not stiffness at the sixth constructional stage^[14-15], the foundational frequency at sixth stage reaches the lowest value, but the

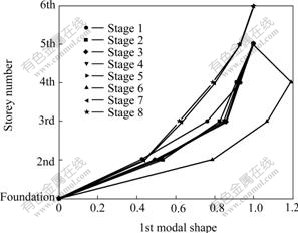
Fig.7 Foundational modal shapes at different construction stages

corresponding damping ratio reaches the highest value. Moreover, the effects are also shown by power spectra curve at the sixth stage in Fig.3: 1) from the amplitude of the power spectrum, both casting fresh concrete components and the shock of operating construction equipment influence more obvious on the second and the third modes than on the foundational one; 2) from the cross power spectrum curve of vibration of the fifth storey, the second and the third modes frequencies are specially less than those of the others, which shift from the second and the third resonance frequencies of the building; and 3) the amplitude of the cross power spectrum curve of vibration of the fifth storey are less than those of the others. And as shown in Fig.7, the foundational modal shape at the sixth stage is different from those of other stages.

As shown in Fig.6, it is obvious that during construction cycle, the foundational modal damping ratios are less than 5% of those of reinforced concrete structure during usage. However, it must be noticed that blocks infilling walls and partition walls were built during testing.

5 Conclusions

1) The effect of casting fresh concrete components and operating constructional devices on dynamic behavior is the most obvious, especially for the higher modes.

2) Dynamic behavior of reinforced concrete frame structure is related to the increasing velocities of both concrete’s time-variant elastic modulus and construction mass from shores and forms.

3) During construction, the modal damping ratios are less than 5% of those of reinforced concrete structure during usage.

References

[1] MEYYAPPA M, PALSSON H, CRAIG J I. Modal parameter estimation for a high-rise building using ambient response data taken during construction [C]// Dynamic Response of Structures: Experi- Mentation, Observation, Prediction and Control. New York: American Society of Civil Engineers, 1980: 141-51.

[2] SCHUSTER N D, VENTURA C E, FELBER A, PAO J. Dynamic characteristics of a 32-storey high-rise building during construction [C]// Proceedings of 5th US Conference on Earthquake Engineering. Chicago: State University of Illinois Press, 1994: 701-710.

[3] MEMARI A M, AGHAKOUCHAK A A, GHAFORY ASHTIANY M. Full-scale dynamic testing of a steel frame building during construction [J]. Engineering Structures, 1999, 21(11): 1115-1127.

[4] ELLIS B R, BOUGARD A J. Dynamic testing and stiffness evaluation of a six-storey timber framed building during construction [J]. Engineering Structures, 2001, 23(10): 1232-1242.

[5] STEPHEN R M, WILSON E L, STANDER N. Dynamic properties of a 30-storey condominium tower building [R]. Report UCB/EERC- 85/03, Department of Civil Engineering, University of California, Berkeley (CA), 1985.

[6] SPARKS P R, JEARYAP D E, SOUZA V C M. A study of the use of ambient vibration measurements to detect changes in the structural characteristics of a building [C]// Dynamic Response of Structures: Experimentation, Observation, Prediction and Control. New York: American Society of Civil Engineers, 1980: 189-200.

[7] MENDOZA L, REYES A, LUCO J E. Ambient vibration tests of the Mexicali General Hospital [J]. Earthquake Spectra, 1991, 7: 281-300.

[8] DIEHL J G. Roof-top ambient vibration measurements [C]// Proceedings of 3rd US National Conference on Earthquake Engineering. Charleston, South Carolina University Press, 1986: 1575-1585.

[9] CLOUGH R W, PENZIEN J. Dynamics of structures [M]. New York: McGraw-Hill, 1975.

[10] ROBERTO P, KURKA G, HERALDO N C. Application of a multivariable input-output subspace identification technique in structural analysis [J]. Journal of Sound and Vibration,2008, 312(3): 461-475.

[11] HERMANS L, AUWERAER V D H. Modal testing and analysis of structures under operational conditions: industrial applications [J]. Mechanical Systems and Signal Processing,1999, 13(2): 193-216.

[12] KHALIL M, ADHIKARI S, SARKAR A. Linear system identification using proper orthogonal decomposition [J]. Mechanical Systems and Signal Processing,2007, 21(8): 3123-3145.

[13] SJOVALL P, ABRAHAMSSON T. Component system identification and state-space model synthesis [J]. Mechanical Systems and Signal Processing,2007, 21(7): 2697-2714.

[14] LU Tie-jian, LI Fang, YU Zhi-wu. Random response of high-layer structures in combined action of horizontal and rocking ground motions [J]. Journal of Central South University: Science and Technology, 2006, 37(3): 623-627. (in Chinese)

[15] WANGHai-bo, SHENPu-sheng. Nonlinear seismic response analysis of reinforced concrete tube in tube structure [J]. Journal of Central South University, 2005, 12(1): 183-188.

(Edited by CHEN Wei-ping)

Foundation item: Project(50678064) supported by the National Natural Science Foundation of China

Received date: 2007-11-18; Accepted date: 2007-12-29

Corresponding author: TIAN Ming-ge, Doctoral candidate; Tel: +86-731-2214300; E-mail: mg_tian@163.com