DOI: 10.11817/j.issn.1672-7207.2015.01.018
基于小波与神经网络的模拟电路故障诊断融合方法
唐圣学,蔡红军,李志刚
(河北工业大学 电磁场与电器可靠性省部共建重点实验室,天津,300130)
摘要:针对信息不足、噪声会导致模拟电路故障诊断效率降低问题,提出基于小波分解、主成分分析和神经网络的信息融合故障诊断方法。为了减少噪声影响和减低故障特征维数,采用该方法对电路测试信号进行小波多尺度分解、主成分分析和归一化预处理。根据不同测试激励源,分别构造独立神经网络完成故障初级定位,进而运用D-S证据融合初级诊断结果实现故障最后定位。研究结果表明:所提方法能充分利用不同信息源对容差下模拟电路故障进行诊断,且定位准确率高。
关键词:故障诊断;神经网络;小波分解;D-S证据推理
中图分类号:TP18 文献标志码:A 文章编号:1672-7207(2015)01-0127-08
Fault diagnosis fusion method for analog circuits based on wavelet and neural network
TANG Shengxue, CAI Hongjun, LI Zhigang
(Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability,
Hebei University of Technology, Tianjin 300130, China)
Abstract: Considering the problem of the low location ratio of analog circuit faults due to the lack of diagnosis information and the noisy interference, a novel fusion method was proposed to diagnose the analog circuit, and analyze the principal component and evident fusion theory based on wavelet decomposition. To reduce the noisy interferences and decrease the dimension of faulty features, the signals of circuit under test were processed with the wavelet decomposition, principal component analysis and normalization. The faults were primarily located by the independent neural networks reconstructed by different testing sources. Then, the final location of faults was implemented by the D-S fusion method with the preliminary results. The results show that the proposed method has the capability to use different information for fault diagnosis of analog circuits under the tolerance and higher accuracy can be obtained.
Key words: fault diagnosis; neural network; wavelet decomposition; D-S evident inference
目前,模拟电路故障诊断智能化程度仍较低,故障定位准确率离实际应用要求仍有差距。然而,模拟电路在许多电子产品及装备中具有不可替代的作用,因此,提升电子产品或装备质量、保证产品安全可靠运行以及减低产品维护成本、实现模拟电路及电子产品自动测试与诊断是一个亟待解决的问题。自20世纪90年代以来,小波技术和神经网络研究快速进展以及这两者相结合,为模拟电路故障的高效自动诊断提供了新的途径和技术支持,在很大程度上提高了模拟电路诊断率,其原因在于这些方法充分利用了小波分解有效提取测试信号时频特征的能力和神经网络强大泛化分类的能力[1-7]。然而,现有结合小波与神经网络的方法在处理多个测试信息时仍存在不足,无法融合多个测试信号信息,故障定位率有待提高[1-2, 4-5, 8]。信息融合技术因能充分应用多个来源信息、能有效解决信息匮乏问题,在电力系统故障诊断[9]、图像滤波[10]、可靠性评估[11]等方面获得了广泛应用。目前,信息融合技术在模拟电路故障诊断得到了初步成果[12-14]。然而,融合技术[12-14]只能处理稳态状态下电路特定频率点的信息融合,无法处理电路瞬态状态下的信息融合,无法去除噪声对测试信号的干扰。在考虑多个测试信号、噪声干扰情况下,本文提出基于小波分析、神经网络和D-S证据理论的模拟电路故障诊断的融合方法。该方法充分发挥小波分析、神经网络和D-S证据技术的各自优势,消除或降低噪声干扰,具有融合多个测试信息和诊断智能化特点。
1 故障诊断策略
诊断过程可分为3个阶段。
1) 测试信号预处理。测试信号经小波分解后提取低频系数能量作为候选故障征兆集,进而经归一化、PCA分析预测处理后构造故障特征向量。每路测试信号都需进行预处理,从而得到各自对应的特征向量。预处理过程减少了噪声对诊断结果的干扰,降低了故障特征维数,从而简化了神经网络分类器的复杂度。
2) 神经网络初级诊断。初级诊断采用单个或单次测试信息,用1个独立的神经网络对电路故障在单信息条件下初次定位。采用测前仿真技术,依据每个测试信号的特征向量维数构造各自对应的神经网络;诊断时根据现场采集信号,各个神经网络都会给出自己独立诊断结果。初级诊断的优点有:① 借助神经网络能很好地实现从征兆空间到故障空间的复杂非线性映射,且具有神经网络所具有的属性,如分布式储存和并行处理、自组织和自学习、泛化能力强,因而智能化程度高;② 采用多个采集测试信号后会导致征兆信息量大增,若所有测试征兆组合为1个故障向量,则此时只需构造1个网络分类器,分类器数量少,但会不可避免地造成该网络结构庞大,训练时间太长,甚至可能无法训练,会降低网络的泛化等能力,影响故障诊断的准确性。采样初级诊断能避免网络结构复杂问题。
3) 融合诊断。每个独立神经网络依据相应测试信息诊断出待测状态属于各故障状态的判决结果,然而,这些判决结果并非完全一致,甚至可能出现较大的偏差或矛盾。融合诊断能有效处理冲突情况。融合诊断任务是把各个独立网络诊断结论作为证据,依据D-S证据推理融合,进而根据融合后证据并结合故障定位规则作出故障决策。D-S融合能充分利用多个信号在空间或时间上的冗余或互补信息,能解释或描述被测电路故障信息的一致性和冲突性,因而能使融合后的故障诊断准确率比单个网络诊断系统的诊断率更高。
基于小波网络与神经网络的融合故障诊断方法如图1所示。由以上分析和图1可看出:该方法结合了小波分析、神经网络和D-S证据推理的优点,具有智能化程度高、定位准确率高、实用化的特点。
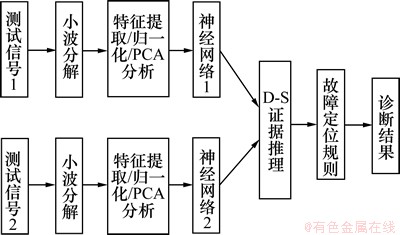
图1 融合故障诊断方法
Fig. 1 Fusion method for fault diagnosis
2 基于小波分解的特征向量构造
若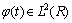 满足
满足 ,则称
,则称 经过伸缩和平移的函数为小波函数簇。令
经过伸缩和平移的函数为小波函数簇。令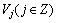 是
是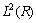 的一多分辨逼近,则一定存在一个标准正交基
的一多分辨逼近,则一定存在一个标准正交基 ,使
,使 ,
,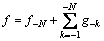 ,且f在
,且f在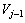 上投影
上投影 为
为 ,称
,称 为
为 在
在 分辨率下的尺度系数,
分辨率下的尺度系数, 为
为 在
在 分辨率下的小波系数。从信号分析的角度看,小波分解具有将信号分解为低频逼近信号(轮廓)和高频细节信号的能力。通常噪声信号主要集中于高频部分。对低频信号进一步分解,就可以得到不同尺度空间的轮廓信号。
分辨率下的小波系数。从信号分析的角度看,小波分解具有将信号分解为低频逼近信号(轮廓)和高频细节信号的能力。通常噪声信号主要集中于高频部分。对低频信号进一步分解,就可以得到不同尺度空间的轮廓信号。
电路参数变化会引起测试信号产生变化,进而导致各尺度空间下小波系数能量变化。因此,文中选择尺度空间下的小波能量表征电路故障征兆,即选为故障特征。小波能量特征获取方法为:对测试信号进行
小波分解,舍去高频系数序列 ,选取低频系数序列
,选取低频系数序列 求取尺度空间j下系数能量
求取尺度空间j下系数能量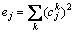 ;继续进
;继续进
行N层分解,得到不同尺度空间下系数能量候选特征向量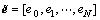 。
。
候选特征向量 维数过高,容易造成神经网络结构复杂,因而需经过PCA降维处理。PCA降维的基本原理是:在尽量保持特征信息不丢失条件下,减少信号中的冗余分量。具体处理过程见参考文献[1]。处理后特征向量为
维数过高,容易造成神经网络结构复杂,因而需经过PCA降维处理。PCA降维的基本原理是:在尽量保持特征信息不丢失条件下,减少信号中的冗余分量。具体处理过程见参考文献[1]。处理后特征向量为 。
。
此外,能量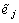 通常比较大,不利于分类BP神经网络构建,因而,需对向量
通常比较大,不利于分类BP神经网络构建,因而,需对向量 进行归一化处理。令
进行归一化处理。令
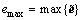 ,
, ,取
,取 (j=0, 1, …, d),则得到归一化能量特征向量
(j=0, 1, …, d),则得到归一化能量特征向量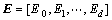 。
。
3 神经网络设计
3.1 神经网络结构设计
本文选用的神经网络结构如图2 所示,输入节点数等于故障特征向量维数,输出节点数等于故障类别数。选用图2所示的单隐层神经网络,这是因为该神经网络结构简单,能逼近任意有理函数,在函数逼近、模式识别等已得到应用[15]。
图2中 为隐层神经元,本文选用sigmoid 函数;
为隐层神经元,本文选用sigmoid 函数; 为输出神经元,本文选用线性函数;
为输出神经元,本文选用线性函数;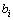 为神经元阈值,
为神经元阈值,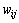 为神经元连接权值。假设输入神经元数为n,输出神经元数为m,那么隐层神经元数h可依据下式选取:
为神经元连接权值。假设输入神经元数为n,输出神经元数为m,那么隐层神经元数h可依据下式选取:

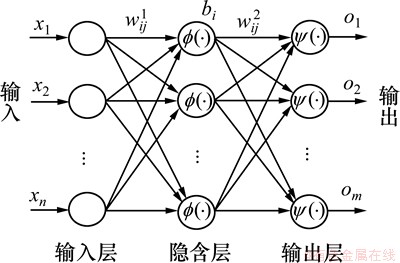
图2 神经网络结构
Fig. 2 Neural network structure
3.2 基于遗传算法的网络学习算法设计
传统神经网络多采用误差方向传播学习算法即BP神经网络。基于BP神经网络的模拟电路故障诊断方法也受到广泛重视[1, 16-18]。然而,BP算法是一种沿梯度下降搜索算法,算法对权向量初始值异常敏感,很容易收敛于局部极小解,影响着故障诊断性能。为解决或克服该问题的影响,本文采用实数编码的遗传算法优化神经网络参数,完成网络学习任务。
遗传算法(GA )模拟自然界生物进化优化机制,能从整个可解空间寻找全局最优解, 避免局部极值,所求解的问题既可适用于非线性不连续函数, 也可以适用于不可微函数优化[19],能较好地克服BP算法优化神经网络中易陷入局部极小值的缺陷。实数编码的遗传算法相对于传统遗传算法效率更高,能克服单二进制编码易引起精度和效率的冲突。
网络学习过程就是根据故障样本集确定图2中神经元阈值bi,神经元连接权值wij。本文隐层节点数n由式确定,不采用遗传算法优化确定,可避免出现过学习,减低网络的泛化能力。因此,遗传优化算法个体(染色体)为x=[b, w],即由权值和阈值组合而成。设训练样本数为S,则网络误差函数Err为

其中: 为第k个样本训练网络时第i个输出神经元的实际输出;
为第k个样本训练网络时第i个输出神经元的实际输出;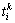 为第k个样本训练网络时第i个输出神经元的期望输出。因此,网络学习问题转化为下列最小优化问题:
为第k个样本训练网络时第i个输出神经元的期望输出。因此,网络学习问题转化为下列最小优化问题:

交叉和变异算子是遗传算法主要运算,直接影响着遗传算法的性能。本文选用2点仿射交叉产生新个体。假设个体X1和X2的具体操作为

式中: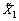 和
和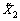 为迭代产生的子代个体;
为迭代产生的子代个体; 和
和 为随机数。若满足
为随机数。若满足 >0,
>0, >0,则称式为算术交叉,是实数遗传算法的传统交叉操作。操作能指导种群个体向最优解子空间靠近。若乘子
>0,则称式为算术交叉,是实数遗传算法的传统交叉操作。操作能指导种群个体向最优解子空间靠近。若乘子 和
和 去掉非负限制, 则称为仿射交叉。仿射交叉除了具有算术交叉操作的优点外, 还能指导算法跳出局部最优解子空间, 因而,平衡了遗传算法的勘探和开采能力。变异算子操作为
去掉非负限制, 则称为仿射交叉。仿射交叉除了具有算术交叉操作的优点外, 还能指导算法跳出局部最优解子空间, 因而,平衡了遗传算法的勘探和开采能力。变异算子操作为 ,
,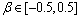 内的随机数。
内的随机数。
个体初值以指数概率分布来随机确定,这样可使遗传算法能够尽可能地搜索到所有可行解的范围。算法效率如时间可根据问题维数和种群规模折中选择。若维数高,则群体规模就应相应增大;若规模太小,则会使染色体得不到充分地交叉和变异,影响收敛速度。
4 基于神经网络与D-S证据推理的故障诊断
4.1 D-S证据基本理论
D-S证据理论用“识别框架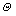 ”表示所感兴趣的命题集。假设集函数:
”表示所感兴趣的命题集。假设集函数: ,满足
,满足

则称m为识别框架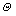 上的基本信度函数分配;式(5)中:
上的基本信度函数分配;式(5)中: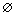 为空集;
为空集;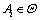 ,表示为第i种模式;
,表示为第i种模式; 称为
称为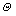 基本信度函数分配值,当
基本信度函数分配值,当 时,称Ai为信度函数上焦元。Ai基本信度函数分配值是可信程度的一种度量。
时,称Ai为信度函数上焦元。Ai基本信度函数分配值是可信程度的一种度量。
设m1, m2, …, mp为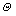 上的p类基本可信度分配,融合推理后基本可信度分配可由下式计算:
上的p类基本可信度分配,融合推理后基本可信度分配可由下式计算:

其中: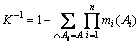 。其中,K为冲突因子,表示证据的冲突程度。
。其中,K为冲突因子,表示证据的冲突程度。 表示证据间存在一致或部分一致,这时证据间可以融合;K越大,表示证据冲突越严重;当
表示证据间存在一致或部分一致,这时证据间可以融合;K越大,表示证据冲突越严重;当 时,表示证据间完全矛盾,此时不能用证据理论融合,可采用修正公式或寻找新的证据[8]。式是D-S证据推理的核心,通过它把各个独立证据组合起来获取融合后基本可信度分配。
时,表示证据间完全矛盾,此时不能用证据理论融合,可采用修正公式或寻找新的证据[8]。式是D-S证据推理的核心,通过它把各个独立证据组合起来获取融合后基本可信度分配。
4.2 神经网络与D-S证据推理的结合
运用D-S证据推理,需要事先确定各证据的信度函数分配 。然而,式和式仅仅给出了公理化定义,没有给出信度函数分配方法,因而常常限制其实际应用。为解决这一限制,在此利用神经网络输出来获取证据理论的信度函数分配。神经网络诊断输出值
。然而,式和式仅仅给出了公理化定义,没有给出信度函数分配方法,因而常常限制其实际应用。为解决这一限制,在此利用神经网络输出来获取证据理论的信度函数分配。神经网络诊断输出值 (
( )的意义是根据相应测试信息估计电路待测状态属于各故障状态的可能性;信度函数
)的意义是根据相应测试信息估计电路待测状态属于各故障状态的可能性;信度函数 意义为根据传感器测试信息表征
意义为根据传感器测试信息表征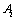 的可信程度。从可能性角度看,两者具有一致性,因而,采用神经网络输出获取信度分配的处理方法是合理的。然而,不能直接用
的可信程度。从可能性角度看,两者具有一致性,因而,采用神经网络输出获取信度分配的处理方法是合理的。然而,不能直接用 代替
代替 ,因为
,因为 不满足式中
不满足式中 要求,为此需进行适当调整。设第i个网络的第j个输出值为
要求,为此需进行适当调整。设第i个网络的第j个输出值为 ,则网络对判断的信度分配为
,则网络对判断的信度分配为

式中:p表示神经网络输出神经元个数, 表示对第i个证据源(神经网络)的信任程度,为信源调整因子。当
表示对第i个证据源(神经网络)的信任程度,为信源调整因子。当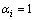 时,满足
时,满足 。
。
4.3 故障定位决策规则
神经网络输出经过式调整后,通过推理式可得融合后的可信度m(A)。基于D-S融合的m(A)故障决策应满足如下规则[18]:故障类别应具有最大的可信度;某故障类别的可信度值与其他类别的可信度的差必须大于某一阈值。设任意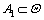 ,
,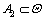 ,且
,且 ,
, 。其中:
。其中: ,
,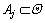 ;i=1, 2, …, p;j=1, 2, …, p;
;i=1, 2, …, p;j=1, 2, …, p;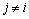 。若满足
。若满足

则A1为故障决策结果。 的作用是为了保证决策结果A1成立的信任度足够大,
的作用是为了保证决策结果A1成立的信任度足够大,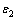 的作用是为了保证决策结果具有足够的区分度而不至于得到模棱两可的决策。在应用中,
的作用是为了保证决策结果具有足够的区分度而不至于得到模棱两可的决策。在应用中, 和
和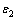 根据实际情况或经验预置。
根据实际情况或经验预置。
5 诊断实例与分析
为了验证本文算法,选取图3所示带通电路进行测试。电路元件参数为:R1=5.18 kΩ,R2=1 kΩ,R3=2 kΩ,C1=C2=5 nF,R4=R5=4 kΩ。元件容差为标称值的10%,电阻容差为标称值的5%,电容容差为标称值的10%。只考虑无容器件电阻电容的单故障,电阻故障值为标称值的 ,电容故障值为标称值的
,电容故障值为标称值的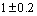 。因此,对于带通电路图3,电阻有10种故障,电容有4种故障,加上无故障电路,总共有15中电路故障状态。
。因此,对于带通电路图3,电阻有10种故障,电容有4种故障,加上无故障电路,总共有15中电路故障状态。
测试激励信号对提高故障诊断率影响很大。通常选用正弦激励源。文献[13-15]依据被测电路的幅频特性分析了正弦激励源的选择方法,选取了关键敏感频率点的正弦激励源。为了提升测试信号的故障信息,本文选择脉宽冲激信号源。被测电路元件参数变化会导致电路性能变化,如传输函数冲激响应体现了传输函数的全部特点。采用冲激激励源有利于使测试响应中含有体现这些变化的丰富时频信息,而不仅仅是个别频率点的信息,同时有利于发挥小波技术在提取时频故障特征的优势。在考虑故障模式和证据间尽量可区分的情况下,通过仿真确定冲激激励源的脉宽宽度。
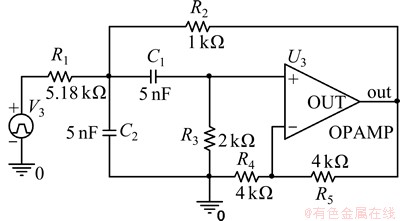
图3 带通测试电路
Fig. 3 Bandpass circuit for test
对于图3所示测试电路,考虑测试成本,选用2个脉冲激励源进行测试和诊断融合。脉冲激励源均为5 V,2个测试源脉冲宽度分别为10 μs(S1)和100 μs(S2)。图4所示为无故障状态和故障C1=6 nF状态下的测试响应输出电压Vout波形图,其中图4(a)测试波形采用的是S1测试源,图4(b)测试波形采用的是S2测试源。由图4可见:2种测试响应(证据体)有一定联系,且噪声严重干扰了测试响应。
对测试响应采用Haar小波提取特征。因为Haar小波具有紧支撑和正则性零点、适合于信号特征的提取。图5和图6所示分别为2级小波分解后的低频特征信号,其中图5所示信号采用S1测试源,图6所示信号采用S2测试源。由图5和图6可见:经过小波处理后,在低频部分无故障和C1故障信号区别明显,有效减少了噪声干扰。在求取能量值特征时,为了减少计算量,只取前面一半数据点进行计算。
构造神经网络分类器。对电路进行正常状态和故障状态模拟,模拟次数为:(元件数×故障类型编号(偏大或偏小)+正常类型编号)×激励源数,即58次。提取激励源S1测试响应特征,特征维数为5,并构造初级分类神经网络NN1结构为5-10-15。激励源S2输入特征维数为6,初级分类神经NN2网络结构为6-12-15。图7所示为网络NN1采用传统遗传算法(GA)和本文GA的训练收敛过程。由图7可见:本文算法在训练神经网络过程中容易跳出局部极值点,能快速收敛于全局极值点。另外,表1所示为采用传统BP算法和本文GA算法训练神经网络的所用时间的比较。从表1可看出:本文算法比BP算法收敛时间短,学习效率高,因此,本文GA算法适用于神经网络的训练学习。
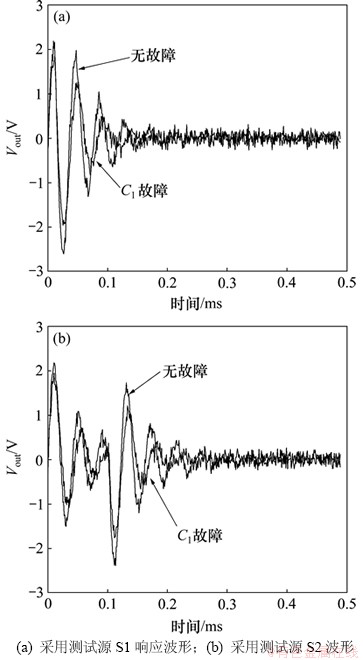
图4 测试响应
Fig. 4 Test responses
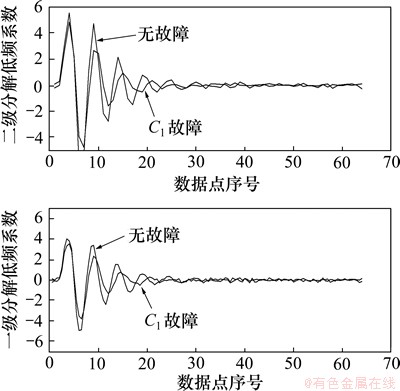
图5 采用测试源S1的2级小波分解后的低频特征
Fig. 5 Low features extracted with two wavelet decompositions for source S1
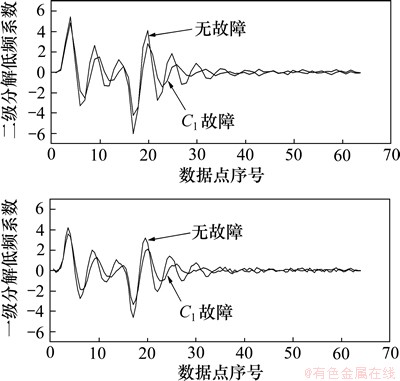
图6 采用测试源S2的2级小波分解后的低频特征
Fig. 6 Low features extracted with two wavelet decompositions for source S2
为了对比单个测试源和多个测试源融合的故障诊断效果,随机选取50个单软故障进行故障识别与定位,其中故障诊断决策参数取 和
和 。表2所示为单独采用神经网络NN1,NN2和采用D-S融合的故障诊断统计结果。从表2可见:融合故障诊断算法(D-S融合)比单个神经网络(NN1和NN2)定位准确度高,误判率和拒判率低,即多源融合诊断系统的性能比单个网络的好,提高了模拟电路故障定位的准确性。这说明本文方法能通过融合不同测试信号的信息来提高模拟电路故障诊断效果。
。表2所示为单独采用神经网络NN1,NN2和采用D-S融合的故障诊断统计结果。从表2可见:融合故障诊断算法(D-S融合)比单个神经网络(NN1和NN2)定位准确度高,误判率和拒判率低,即多源融合诊断系统的性能比单个网络的好,提高了模拟电路故障定位的准确性。这说明本文方法能通过融合不同测试信号的信息来提高模拟电路故障诊断效果。
为了进一步说明本文方法的有效性,采用本文方法对4运放双二次高通滤波器进行故障诊断,其中4运放双二次高通滤波器如图8所示。图8中参数为标称参数,元件容差及故障设置与文献[19]中的相同。表3所示为采用BP前向网络和GB网络在不同拓扑结构下的诊断结果。由表3可知:无论采用BP前向网络还是GA网络,D-S融合都有利于提高故障诊断率,但采用GA效果更好。因此,本文方法能更加有效地提高故障诊断率。
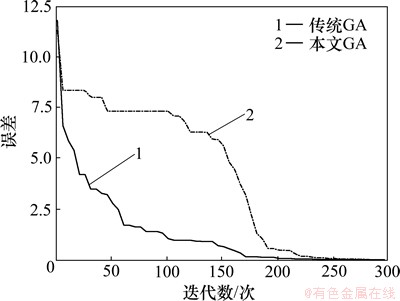
图7 神经网络NN1训练收敛过程
Fig. 7 Convergence process of neural network NN1
表1 训练时间比较
Table 1 Comparison of training time min
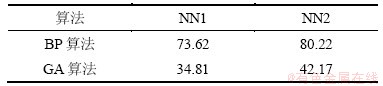
表2 故障诊断结果
Table 2 Results of fault diagnosis %
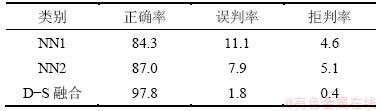
表3 高通滤波器故障诊断结果
Table 3 High pass filter results of fault diagnosis
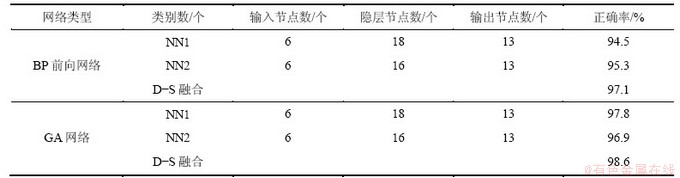
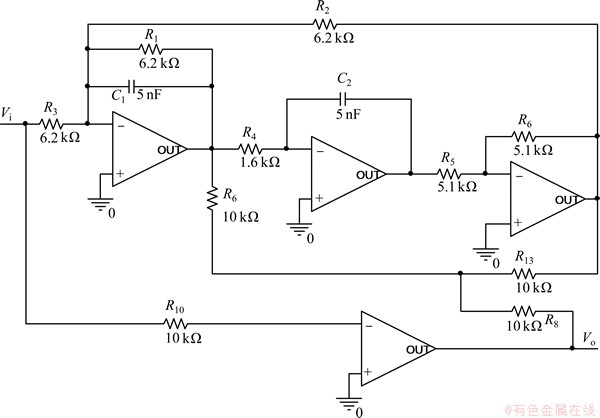
图8 4运放高通滤波器
Fig. 8 Four op-amp high pass filter
6 结论
1) 研究了小波技术、神经网络和证据推理相结合的模拟电路故障诊断的融合方法。该方法能有效去除噪声干扰,减小故障特征维数,能融合多个故障信息进行故障定位,具有智能化程度高的特点。
2) 神经网络训练采用了改进GA算法来优化结构和阈值,能较快地收敛到全局最优。利用神经网络初级诊断结果完成D-S证据推理的信度分配函,实现了D-S证据推理的模拟电路故障融合诊断,有效提高了故障定位的准确率。融合方法具有很强的鲁棒性,能有效完成容差情况下的模拟电路软故障诊断。
参考文献:
[1] Aminian M, Aminian F. Neural-network based analog-circuit fault diagnosis using wavelet transform as preprocessor[J]. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 2000, 47(2): 151-156.
[2] Spyronasios A D, Dimopoulos M G, Hatzopoulos A A. Wavelet analysis for the detection of parametric and catastrophic faults in mixed-signal circuits[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(6): 2025-2038.
[3] Stopjaková V, Malosek P, Matej M, et al. Defect detection in analog and mixed circuits by neural networks using wavelet analysis[J]. IEEE Transactions on Reliability, 2005, 54(3): 441-448.
[4] 谢宏, 何怡刚, 吴杰. 基于小波-神经网络模拟电路故障诊断方法的研究[J]. 仪器仪表学报, 2004, 25(5): 672-675.
XIE Hong, HE Yigang, WU Jie. Research on analog circuit fault diagnostic method based on wavelet-neural network[J]. Chinese Journal of Scientific Instrument, 2004, 25(5): 672-675.
[5] 金瑜, 陈光 , 刘红. 基于小波神经网络的模拟电路故障诊断[J]. 仪器仪表学报, 2007, 28(9): 1600-1604.
, 刘红. 基于小波神经网络的模拟电路故障诊断[J]. 仪器仪表学报, 2007, 28(9): 1600-1604.
JIN Yu, CHEN Guangju, LIU Hong. Fault diagnosis of analog circuit based on wavelet neural network[J]. Chinese Journal of Scientific Instrument, 2007, 28(9): 1600-1604.
[6] 钟建林, 何友, 王红星. 基于多频小波分析和 D-S推理的电路故障诊断[J]. 电工技术学报, 2010, 25(8): 180-184.
ZHONG Jianlin, HE You, WANG Hongxing. Circuit fault diagnosis based on multi-frequency wavelet analysis and D-S reasoning[J]. Transactions of China Electrotechnical Society, 2010, 25(8): 180-184.
[7] 马岚, 王厚军. 基于复互小波分析的模拟电路故障诊断方法[J]. 电子科技大学学报, 2013, 42(3): 380-384.
MA Lan, WANG Houjun. Faults diagnosis approach for analog circuit based on complex cross-wavelet transform[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(3): 380-384.
[8] 丛伟, 景博, 于宏坤. 基于 KPLS 特征提取的WNN模拟电路软故障诊断[J]. 中南大学学报(自然科学版), 2014, 45(6): 1841-1846.
CONG Wei, JING Bo, YU Hongkun. WNN soft fault diagnosis of analog circuit based on KPLS feature extraction[J]. Journal of Central South University (Science and Technology), 2014, 45(6): 1841-1846.
[9] 符玲, 何正友, 麦瑞坤, 等. 小波熵证据的信息融合在电力系统故障诊断中的应用[J]. 中国电机工程学报, 2008, 28(13): 64-69.
FU Ling, HE Zhengyou, MAI Ruikun, et al. Information fusion method of entropy evidences and its application to fault diagnosis in power system[J]. Proceedings of the CSEE, 2008, 28(13): 64-69.
[10] 李剑锋, 乐光新, 尚勇. 基于改进型 D-S证据理论的决策层融合滤波算法式[J]. 电子学报, 2004, 32(7): 1160-1164.
LI Jianfeng, YUE Guangxin, SHANG Yong. Decision-level fusion filtering algorithm based on advanced D-S theory of evidence[J]. Acta Electronica Sinica, 2004, 32(7): 1160-1164.
[11] 周旷, 师义民. 一种改进的证据组合规则在可靠性评估中的应用[J]. 火力与指挥控制, 2012, 37(11): 191-194.
ZHOU Kuang, SHI Yimin. Application of a modified evidence combination rule in reliability assessment[J]. Fire Control & Command Control, 2012, 37(11): 191-194.
[12] 彭敏放, 何怡刚, 吕敬祥. 基于智能信息融合的模拟电路故障定位方法[J]. 电工技术学报, 2005, 20(11): 93-96.
PENG Minfang, HE Yigang, LU Jingxiang. Fault location of analog circuits using intelligent information fusion technology[J]. Transactions of China Electrotechnical Society, 2005, 20(11): 93-96.
[13] 彭敏放, 何怡刚, 贺建飚. 模拟电路的融合智能故障诊断[J]. 中国电机工程学报, 2006, 26(3): 19-24.
PENG Minfang, HE Yigang, HE Jianbiao. Synthetic intelligence based fault diagnosis of analog circuits[J]. Proceedings of the CSEE, 2006, 26(3): 19-24.
[14] 彭敏放, 何怡刚, 王耀南. 基于神经网络与证据理论的模拟电路故障诊断[J]. 电路与系统学报, 2005, 10(1): 35-39.
PENG Minfang, HE Yigang, WANG Yaonan. Fault diagnosis of analog circuits based on neural network and evidence theory[J]. Journal of Circuits and Systems, 2005, 10(1): 35-39.
[15] 张代远. 神经网络新理论与方法[M]. 北京: 清华大学出版社, 2006: 47-62.
ZHANG Daiyuan. New neural network theory and method[M]. Beijing: Tsinghua University Press, 2006: 47-62.
[16] YUAN Lifeng, HE Yignag, HUANG Jiaoying, et al. A new neural-network-based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(3): 586-595.
[17] 林海军, 张礼勇, 任殿义, 等. 基于Wiener核和BP神经网络的非线性模拟电路故障诊断[J]. 仪器仪表学报, 2009, 30(9): 1946-1949.
LIN Haijun, ZHANG Liyong, REN Dianyi, et al. Fault diagnosis in nonlinear analog circuit based on Wiener kernel and BP neural network[J]. Chinese Journal of Scientific Instrument, 2009, 30(9): 1946-1949.
[18] 谢宏, 何怡刚, 周应堂, 等. 小波神经网络在模拟电路故障诊断中的应用研究[J]. 湖南大学学报(自然科学版), 2004, 31(4): 38-40.
XIE Hong, HE Yigang, ZHOU Yingtang, et al. Application of wavelet and neural network in analog circuit fault location[J]. Journal of Hunan University (Natural Sciences), 2004, 31(4): 38-40.
[19] Siddique M, Tokhi M. Training neural networks: back propagation vs. genetic algorithms[C]// International Joint Conference on Neural Networks, IEEE 2001 Proceedings. Washington D C, 2001: 2673-2678.
[20] 何友. 多传感器信息融合及应用[M]. 北京: 电子工业出版社, 2000: 58-88.
HE You. Multi-sensor information fusion and its applications[M]. Beijing: Electronic Industry Press, 2000: 58-88.
[21] 肖迎群, 何怡刚. 基于脊波网络的模拟电路故障诊断[J]. 电工技术学报, 2010, 25(6): 155-162.
XIAO Yingqun, HE Yigang. A fault diagnosis method of analog circuit based on ridgelet network[J]. Transactions of China Electrotechnical Society, 2010, 25(6): 155-162.
(编辑 陈灿华)
收稿日期:2014-01-10;修回日期:2014-03-15
基金项目(Foundation item):国家自然科学基金资助项目(51477040,51377044);教育部博士点基金资助项目(20121317110008) (Projects(51477040, 51377044) supported by the National Natural Science Foundation of China; Project(20121317110008) supported by Doctoral Fund of Ministry of Education of China)
通信作者:唐圣学,博士,硕士生导师,从事电路故障诊断与可靠性研究;E-mail: tshxue@126.com