脉冲电流作用下纯铝熔体凝固晶核的迁移行为
来源期刊:中国有色金属学报(英文版)2014年第1期
论文作者:李希彬 芦凤桂 崔海超 唐新华
文章页码:192 - 198
关键词:脉冲电流;凝固;细化机制;晶核迁移;数值模拟
Key words:electric current pulse; solidification process; grain refinement mechanism; migration behavior; numerical simulation
摘 要:建立凝固过程的数学模型来揭示自由晶核的迁移行为。模拟结果表明:在脉冲电流作用下,大多数形成于熔体上表面的晶核将往下迁移并随机分布于Al熔体内部,提供更多的形核质点,进而细化凝固组织晶粒。同时,研究在施加脉冲电流(ECP)时晶核尺寸对晶核分布和细化的影响。小尺寸的晶核同周围熔体一同运动,迁移距离较短;而大尺寸的晶核在脉冲电流作用下以较快的速度相对于周围熔体运动,有利于熔体内部晶粒的细化。该研究有利于加深对脉冲电流细化凝固组织机理的认识。
Abstract: A mathematical model considering free nuclei was developed to reveal the migration behavior of the free nuclei. Numerical simulation results show that most of the nuclei on the top surface of the melt move downwards and distribute randomly inside the Al melt, which induces more nucleation sites resulting in grain refinement. At the same time, the effect of nuclei size on the nuclei distribution and refinement employing electric current pulse (ECP) was also investigated. The smaller nuclei migrate a short distance with the Al melt at lower speed. But for the larger nuclei, the migration downwards with higher speed benefits the refinement of interior grains of the melt. The research results help to better understand the refinement process and provide a more reasonable explanation of the grain refinement mechanism using ECP.
Trans. Nonferrous Met. Soc. China 24(2014) 192-198
Xi-bin LI, Feng-gui LU, Hai-chao CUI, Xin-hua TANG
School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
Received 23 February 2013; accepted 5 July 2013
Abstract: A mathematical model considering free nuclei was developed to reveal the migration behavior of the free nuclei. Numerical simulation results show that most of the nuclei on the top surface of the melt move downwards and distribute randomly inside the Al melt, which induces more nucleation sites resulting in grain refinement. At the same time, the effect of nuclei size on the nuclei distribution and refinement employing electric current pulse (ECP) was also investigated. The smaller nuclei migrate a short distance with the Al melt at lower speed. But for the larger nuclei, the migration downwards with higher speed benefits the refinement of interior grains of the melt. The research results help to better understand the refinement process and provide a more reasonable explanation of the grain refinement mechanism using ECP.
Key words: electric current pulse; solidification process; grain refinement mechanism; migration behavior; numerical simulation
1 Introduction
Electric current pulse (ECP) plays an important role in materials processing, especially in the field of metal solidification [1-4]. It has been testified that the ECP can effectively refine the solidification structure of metal materials [5-10], resulting in high mechanical properties of metallic materials [11,12]. In recent years, more attentions have been paid to revealing the refinement mechanism of the ECP on the solidification structure, and several theories regarding the grain refinement mechanism of the ECP have been proposed. DING et al [13,14] analyzed the effect of the ECP on the electromagnetic field and flow field of Ti-Al melt based on numerical simulation, but the effect of the ECP with respect to resultant microstructure was not clarified. ZHAO et al [15] inferred that the change of solidification structure is resulted from electromagnetic pulse, which could induce the forced convection in the melt and result in the fragmentation of dendrite during the solidification. However, the movement of the fragmentation and its influence on the nucleus rate have not been further investigated. ZHAI et al [16-19] investigated the refinement mechanism of the ECP on the solidification structure of pure Al systematically and proved that the nucleus rate increases with applying the ECP during the initial nucleation stage of the melt and that the ECP makes crystal nuclei on the top surface of the melt fall down and move freely in the molten metal, which promotes the refinement of solidification structure. However, a more detailed explanation about the migration behavior of crystal nuclei under the effect of the ECP lacked explicit research. In our previous study [20], the temperature field and flow field of the melt after applying the ECP were calculated based on the mathematic model, by which the fluctuation of the Al liquid surface could lead to the generation of more nuclei after applying the ECP. But the movement of the free nuclei, the crucial factor for the refinement mechanisms, was not considered in that model. Therefore, a further research is necessary to better understand the mechanism of grain refinement with the ECP.
In the present study, a three-dimensional mathematical model is developed to simulate migration behavior of the free nuclei under the effect of the ECP. The heat effect, electromagnetic effect and mechanical effect caused by the ECP are considered in this model and the nucleus movement is analyzed coupling with fluid flow. The calculated results with this model describe the nuclei migration and distribution under the effect of the ECP, and also clarify its relationship with the resultant microstructure.
2 Physical and mathematical models
2.1 Physical model of solidification process
Figure 1 shows the geometric model of the solidification process. The dimensions of silica sand mould are d50 mm×75 mm and d40 mm×65 mm for cavity. The paralleled steel electrodes with dimensions of d3 mm×8 mm are inserted into the Al melt from the top surface. The electrodes immersed into Al melt are 4 mm in length and 2 mm away from the sidewall. The ECP is applied to the pure Al melt through the parallel electrodes.

Fig. 1 Schematic of physical model of pure Al with ECP
2.2 Mathematical model
The finite difference method incorporating the volume of fluid (VOF) method is employed to calculate the momentum and energy transport of the melt. Some assumptions for the subsequent calculation and simulation are given as follows: 1) the fluid flow is assumed to be Newtonian, laminar, and incompressible; 2) the melt is assumed to be nonpolar; 3) the nuclei are assumed to be generated on the top surface of the melt.
2.2.1 Governing equations
The differential equations governing the conservation of mass, momentum, and energy based on continuum formulation are used to describe the heat and mass transfer and fluid flow as follows:
Momentum equation:
 (1)
(1)
Mass continuity equation:
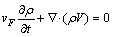 (2)
(2)
Energy equation:
 (3)
(3)
where ρ is the fluid density; v is the molten metal velocity; t is the time; μ is the dynamic viscosity; p is the hydrodynamic pressure; RSOR is the mass source, including the nuclei mass; Fb is the body force (e.g. gravity, buoyancy and electromagnetic force); γ is the surface tension; vF is the fractional volume open to flow; E is the internal energy per unit mass; k is thermal conductivity; T is the local temperature; and ESOR is the energy source term generated by pulse current.
2.2.2 Volume-of-fluid (VOF) method
The VOF method is taken to track sharp interface through a fixed grid of control volumes [21]. The configuration of the interface in computational elements is reconstructed according to the value of F in VOF, where F is described as follows:
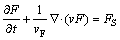 (4)
(4)
where F represents the volume fraction occupied by the fluid.
2.2.3 Electromagnetic model
The ECP is applied to the melt through the parallel electrodes, leading to cyclic magnetic field and in reverse inducing cyclic electric current. The distribution of electromagnetic field is governed by Maxwell’s equations [22] as follows:
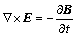 (5)
(5)
 (6)
(6)
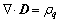 (7)
(7)
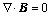 (8)
(8)
The electromagnetic constitutive equations of simple isotropic material mediums can be expressed as
 (9)
(9)
 (10)
(10)
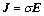 (11)
(11)
where E is the electric field; B the is magnetic flux density; t is the time; H is the intensity of magnetic field; D is the electric displacement; J is the vector of current density; ρq is the density of free charge; μ is the vacuum permittivity; and σ is the conductivity.
The Joule heating generated by the current can be expressed as
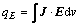 (12)
(12)
The equation of the Lorentz force is described as follows:
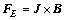 (13)
(13)
2.2.4 Boundary conditions
The heat transfer at the interface between the sand mould and the melt can be described as follows [23]:
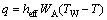 (14)
(14)
where heff is the heat transfer coefficient between sand mould and the melt; T is the fluid surface temperature; WA is the heat-structure surface area; TW is the surface temperature of the mould.
Boundary conditions on the top surface containing the free surface can be described as follows [24]:
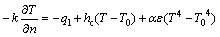 (15)
(15)
where k is the thermal conduction; hc is the convection coefficient; α is the Stefan–Boltzmann constant; and ε is the emissivity.
2.2.5 Nuclei model
The initial distribution status of nuclei is very important in analyzing the nuclei migration behavior. According to the former research carried out by LI et al [17], the nuclei mainly form on the top surface of the melt. Assume that the nuclei generate on the top surface of the melt and neglect the nuclei produced in other places, which helps to observe the migration process of the nuclei clearly. In addition, the heat transfer of nuclei to fluid and its temperature are omitted.
The dynamics equation of the mass nuclei is as follows:
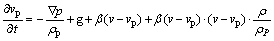 (16)
(16)
where vp and ρp are the nuclei mean velocity and density, respectively; g includes gravity and other body force; v and p are the fluid velocity and pressure, respectively; β is the drag coefficient between nuclei and the melt.
Coupling calculation with the fluid, initial nuclei velocity value is given and then velocity is updated by the results calculated as follows:
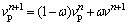 (17)
(17)
where
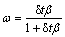 (18)
(18)
Then the fluid velocity is calculated depending on the nuclei velocity as follows:
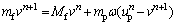 (19)
(19)
where β is the drag coefficient; δt is the calculated time increment;  and vn are the velocity of nuclei and the melt in the control volume; mf and mp are the mass of melt in the control volume and nuclei mass, respectively.
and vn are the velocity of nuclei and the melt in the control volume; mf and mp are the mass of melt in the control volume and nuclei mass, respectively.
The different electromagnetic forces are imposed on nuclei and the melt respectively for their different electric conductivities. The relevant force imposed on the nuclei can be expressed as
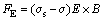 (20)
(20)
where σs is the electric conductivity of the nuclei and σ is the electric conductivity of the melt.
2.3 Numerical procedure
The basic procedure for advancing a solution through one small increment in time δt is as follows: 1) Explicit approximations of the conservation of momentum are used to compute the first guess for new time-level velocities using the initial conditions or previous time-level values for pressure. 2) To satisfy the mass continuity, when the implicit option is used, the pressures are iteratively adjusted at each cell and the velocity variation generated by each pressure change is added to the velocities computed in Step 1. 3) When there is a free-surface or fluid interface, the VOF method must be used to give the new fluid configuration. 4) Electromagnetic equations are used to calculate electro-magnetic force as body force in the domain of the melt. 5) Energy equation is solved using explicit option to get the new temperature distribution and the thermal properties of the melt are updated. 6) Equation (1) is used to calculate the velocity of the nucleus.
Repetition of the above steps will advance a solution through any desired time interval. At each step, corresponding boundary conditions will be imposed at all meshes.
3 Results and discussion
The thermo physical properties for the Al melt and nucleus are listed in Table 1 [24,25]. The Al melt is filled in the mould with 64.65 mm height and 936 K initial temperature, and ECP is applied to the melt through paralleled electrodes on the top surface. The peak current of the pulse is 100 A, the pulse frequency is 100 Hz and pulse width is 200 μs. The nuclei are formed on the top surface of the melt at a certain rate.
3.1 Migration behavior of nuclei under effect of ECP
With the application of ECP, the melt flows under the combined effects of Lorentz force, surface tension and buoyancy, which make the temperature field change greatly in this condition [20]. At the same time, the nuclei generating on the top surface of the melt migrate to the other places of the cavity. Figure 2 shows the migration process of the nuclei with a diameter of 50 μm from t=0.1 s to t=2 s with ECP. At 0.1 s, the free nuclei move downwards from the top surface with a slow initial velocity in a short distance. From t=0.4 s to t=0.7 s, the nuclei speed up under the effect of the gravity and electromagnetic force, moving to the inner part of the cavity, which results in the fine crystals. With time going on, the nuclei arrive at the bottom of the cavity at t=1 s, which shows that fine grain would be achieved for the entire cavity if continually applying the ECP. From t=1.5 s to t=2 s, more nuclei generating on the top surface move to the inner part of the cavity and distribute more evenly. The process of nuclei migration with time showed that the employment of the ECP promotes the nuclei movement leading to fine grain, and that increasing existence time of the ECP causes the fine grain for entire cavity.
Table 1 Thermo physical properties of Al melt and related parameters

The gravity and electromagnetic force drive the nuclei to move downwards in cavity. The density difference between the nucleus and melt makes the nuclei tend to move downwards. And the higher electric conductivity of nucleus leads to the large magnetic force imposed on the nucleus. When the resultant force imposed on the nucleus is larger than the resistance of the surrounding melt, the nuclei have tendency to migrate downwards.
The flow fluid of the melt also plays an important role in the nuclei migration process. Figure 3 shows that the melt on the surface flows inwards and downwards, and also the melt close to the wall flows upwards in the upper part of the cavity, with the results of the nuclei densely distributing in the center of the cavity and sparsely distributing near to the wall from t=0.1 s to t=1.5 s. In our previous research, the fluctuation phenomenon in the melt surface was observed in both numerical simulation [20] and experimental research [17], which is beneficial to produce more nuclei on the top surface and provide more nuclei to the interior of the melt.

Fig. 2 Nuclei movement and distribution under effect of ECP

Fig. 3 Flow field of melt under influence of ECP
It can be concluded that once crystal nuclei exist on the top surface of the melt, these nuclei would be brought into the interior of the cavity and distributed evenly under the combination of gravity, magnetic force and the flow of the melt. The increase of the number of nuclei in the melt finally leads to the refinement of solidification structure. LI et al [17] carried out similar experimental research and set a net in the middle of the cavity to divide the melt into two parts. Fine grains were found above the net, while coarse columnar crystals existed in the lower part under the net after applying the ECP with parallel electrodes. The experimental results show that the nuclei migrate downwards from the top of the melt, so the present simulation results are well verified by the experimental phenomenon.
3.2 Effect of nucleus size on migration behavior of nuclei
In order to investigate the effect of nucleus size on migration behavior, the migration process of nuclei with different sizes is simulated based on this model. It should be pointed out that the size of the nucleus is assumed for comparison of migration process in calculation.

Fig. 4 Distribution of nuclei with different sizes under influence of ECP
Figure 4 shows distribution of the nuclei with different sizes at t=0.5 s with the ECP. When the diameter of the nucleus is smaller than 10 μm, as shown in Figs. 4 (a)-(c), it is hard to change the distributions of nuclei at t=0.5 s. The nuclei move to the middle of the electrodes with small downward movement distance, especially for smaller size, as shown in Fig. 4(a). The surface area of the nucleus is relatively large for the nucleus in smaller size, and the viscous resistance caused by the surrounding melt makes it more difficult to move downwards. In this case, the migration process of the nuclei mainly depends on melt flow. From Figs. 4(d)-(f), it can be concluded that the nuclei move into the interior of the melt obviously for the increase of the nucleus size with the ECP. Furthermore, the larger the size of the nucleus is, the farther the nucleus moves away from the top surface. And when their sizes are big enough, the nuclei can arrive at the bottom of the cavity in a short time due to relatively small viscous resistance. The gravity and electromagnetic force finally results in the downward movement of the nuclei compared to the surrounding melt. It should be noticed that the flow field of the melt also has an important influence on the migration process of the nuclei in large size.
The size of the nucleus is variable in the process of solidification. On one hand, the size of the nucleus keeps growing after exceeding the critical size based on the thermodynamics conditions of solidification. On the other hand, the nucleus may become smaller for sake of temperature variation. Figure 5 shows the temperature field of the melt at t=0.5 s, the temperature inside cavity is very high, which probably makes nuclei become smaller or even be re-melted if their size is not big enough during the migrate process. When the nucleus becomes smaller, the viscous resistance imposed on them will prevent them from moving downwards. So, only the nuclei with large size can move and arrive at the bottom of the cavity.

Fig. 5 Temperature field of pure Al melt after applying ECP
4 Conclusions
1) A mathematical model considering the free nuclei is developed to reveal the nuclei migration process and analyze the effect of the grain size on nuclei distribution under the effect of the ECP.
2) The numerical simulation results show that most of nuclei on the top surface of the melt will move downwards under the combined effects of gravity, electromagnetic force and flow field of the melt and will be distributed randomly inside the Al melt. This migration behavior would induce more nucleation sites leading to the refinement of solidification structure with applying the ECP.
3) The smaller nuclei would migrate downward a short distance together with the Al melt at a lower speed. On the contrary, the larger nuclei could migrate to the bottom of cavity with a higher speed, which is beneficial to the refinement in the interior of the melt. But not all the nuclei with larger size could move to the interior of the melt for becoming smaller or even re-melting during the migration process in the melt at a high temperature.
References
[1] BOETTINGER W J, CORIELL S R, GREER A L, KARMA A, KURZ W, RAPPAZ M, TRIVEDI R. Solidification microstructures: Recent developments, future directions [J]. Acta Materialia, 2000, 48(1): 43-70.
[2] CONRAD H. Effects of electric current on solid state phase transformations in metals [J]. Materials Science and Engineering A, 2000, 287(2): 227-237.
[3] LI F, REGEL L L, WILCOX W R. The influence of electric current pulses on the microstructure of the MnBi/Bi eutectic [J]. Journal of Crystal Growth, 2001, 223(1-2): 251-264.
[4] ZHANG Qi, WANG Tong-min, LI Ting-ju, JIN Jun-ze. Numerical simulation of solidification process of Sn-3.5%Pb hollow billet with stirring magnetic field [J]. Transactions of Nonferrous Metals Society of China, 2007, 17(5): 940-946.
[5] NAKADA M, SHIOHARA Y, FLEMINGS M C. Modification of solidification structures by pulse electric discharging [J]. ISIJ International, 1990, 30(1): 27-33.
[6] LI J, LIN H. Modification of solidification structure by pulse electric discharging [J]. Scripta Metallurgica et Materialia, 1994, 31(12): 1691-1694.
[7] BARNAK J, SPRECHER A, CONRAD H. Colony (grain) size reduction in eutectic Pb-Sn castings by electroplusing [J]. Scripta Metallurgica et Materialia, 1995, 32(6): 879-884.
[8] BRUSH L N, GRUGEL R N. The effect of an electric current on rod-eutectic solidification in Sn-0.9wt.% Cu alloys [J]. Materials Science and Engineering A, 1997, 238(1): 176-181.
[9] LAI Z H, CONRAD H, TENG G Q, CHAO Y S. Nanocrystallization of amorphous Fe-Si-B alloys using high current density electropulsing [J]. Materials Science and Engineering A, 2000, 287(2): 238-247.
[10] YIN Zhen-xing, LIANG Dong, CHEN Yu-e, CHENG Yu-feng, ZHAI Qi-jie. Effect of electrodes and thermal insulators on grain refinement by electric current pulse [J]. Transactions of Nonferrous Metals Society of China, 2013, 23: 92-97.
[11] GAO M, HE G H, YANG F, GUO J D, YUAN Z X, ZHOU B L. Effect of electric current pulse on tensile strength and elongation of casting ZA27 alloy [J]. Materials Science and Engineering A, 2002, 337(1-2): 110-114.
[12] WANG Jian-zhong, CHEN Qing-fu, CAO Li-yun, ZHAO Lian-cheng. Effect of electropulse modification parameters on ingot macrostructure of Cu-Al-Ni shape memory alloys [J]. Transactions of Nonferrous Metals Society of China, 2002, 12(3): 400-404.
[13] DING H, ZHANG Y, JIANG S, CHEN R, GUO J. Effects of harmonic electric field frequency on electromagnetic and flow fields of Ti-Al melt in a rectangular mold based on numerical simulation [J]. Research & Development, 2010, 7(4): 377-382.
[14] ZHANG Yong, DING Hong-sheng, JIANG San-yong, CHEN Rui-run, GUO Jing-jie. Numerical simulation of electromagnetic and flow fields of Tial melt under electric field [J]. Chian Foundry, 2010, 7(3): 241-247.
[15] ZHAO Z, WANG J, LIU L. Grain refinement by pulse electric discharging and undercooling mechanism [J]. Materials and Manufacturing Processes, 2011, 26(2): 249-254.
[16] LIAO X, ZHAI Q, LUO J, CHEN W, GONG Y. Refining mechanism of the electric current pulse on the solidification structure of pure aluminum [J]. Acta Materialia, 2007, 55(9): 3103-3109.
[17] LI J, MA J, GAO Y, ZHAI Q. Research on solidification structure refinement of pure aluminum by electric current pulse with parallel electrodes [J]. Materials Science and Engineering: A, 2008, 490(1-2): 452-456.
[18] MA J, LI J, GAO Y, ZHAI Q. Grain refinement of pure Al with different electric current pulse modes [J]. Materials Letters, 2009, 63(1): 142-144.
[19] MA J H, LI J, GAO Y L, JIA L X, LI Z, ZHAI Q J. Effect of peak value and discharge frequency of electric current pulse on solidification structure of Fe-1C-1.5Cr bearing steel [J]. Ironmaking and Steelmaking, 2009, 36(4): 286-290.
[20] LI X B, LU F G, CUI H C, TANG X H. Effect of electric current pulse on flow behavior of Al melt in parallel electrode process [J]. Materials Science and Technology, 2013, 29(2): 226-233.
[21] HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries [J]. Journal of Computational Physics, 1981, 39(1): 201-225.
[22] JACKSON J D, FOX R F. Classical electrodynamics [J]. American Journal of Physics, 1999, 67: 841-845.
[23] GOLDSTEIN H, POOLE C, SAFKO J, ADDISON S R. Classical mechanics [J]. American Journal of Physics, 1980, 70: 782-784.
[24] GAO Z, WU Y, HUANG J. Analysis of weld pool dynamic during stationary laser–MIG hybrid welding [J]. The International Journal of Advanced Manufacturing Technology, 2009, 44(9): 870-879.
[25] MURPHY A B. A self-consistent three-dimensional model of the arc, electrode and weld pool in gas–metal arc welding [J]. Journal of Physics D: Applied Physics, 2011, 44(19): 194009.
李希彬,芦凤桂,崔海超,唐新华
上海交通大学 材料科学与工程学院,上海 200240
摘 要:建立凝固过程的数学模型来揭示自由晶核的迁移行为。模拟结果表明:在脉冲电流作用下,大多数形成于熔体上表面的晶核将往下迁移并随机分布于Al熔体内部,提供更多的形核质点,进而细化凝固组织晶粒。同时,研究在施加脉冲电流(ECP)时晶核尺寸对晶核分布和细化的影响。小尺寸的晶核同周围熔体一同运动,迁移距离较短;而大尺寸的晶核在脉冲电流作用下以较快的速度相对于周围熔体运动,有利于熔体内部晶粒的细化。该研究有利于加深对脉冲电流细化凝固组织机理的认识。
关键词:脉冲电流;凝固;细化机制;晶核迁移;数值模拟
(Edited by Chao WANG)
Foundation item: Project (SELF-2011-01) supported by the Open Project of Shanghai Key Laboratory of Modern Metallurgy and Materials Processing, China; Projects (51204109, 51035004) supported by the National Natural Science Foundation of China
Corresponding author: Feng-gui LU; Tel/Fax: +86-21-34202814; E-mail: lfg119@sjtu.edu.cn
DOI: 10.1016/S1003-6326(14)63047-8

