J. Cent. South Univ. (2018) 25: 1437-1446

DOI: https://doi.org/10.1007/s11771-018-3838-0

RFD-Rao and RFD-Wald tests for distributed targets with range walking effect

WANG Yu(王宇)¹, CAO Yun-he(曹运合)^{1, 2}, SU Hong-tao(苏洪涛)^{1, 2}, WANG Sheng-hua(王胜华)¹

1. National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China;

2. Collaborative Innovation Center of Information Sensing and Understanding, Xidian University,Xi’an 710071, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: Two novel adaptive distributed target detectors, the range frequency domain-Rao (RFD-Rao) and range frequency domain-Wald (RFD-Wald) tests are proposed in this work. The application methods for these tests consider a partially homogeneous disturbance environment and a target range walking effect in a coherent processing interval (CPI). The asymptotic performance of the detectors is analyzed, and the constant false alarm rate (CFAR) properties with respect to the clutter covariance matrix and power level are shown. The performances of the proposed adaptive detectors are assessed through Monte–Carlo simulations, and the results are presented to demonstrate the effectiveness of the proposed detection algorithms compared to those of similar existing detectors.

Key words: adaptive detection; distributed target; Rao test; Wald test; range walking

Cite this article as: WANG Yu, CAO Yun-he, SU Hong-tao, WANG Sheng-hua. RFD-Rao and RFD-Wald tests for distributed targets with range walking effect [J]. Journal of Central South University, 2018, 25(6): 1437–1446. DOI: https://doi.org/10.1007/s11771-018-3838-0.

1 Introduction

The problem in detecting distributed targets for wideband radar signals embedded in disturbance has received considerable attention in recent years in the radar community [1–5]. The range resolution is always smaller than the target size in wideband waveforms, and thus the target returns are distributed into multiple range cells, which are called high range resolution profiles (HRRPs). These targets are considered as range spread targets or distributed targets in the literature. High range resolution reduces the energy per range cell backscattered from the distributed clutter, and the resolved target scatters have less radar cross-section fluctuation than those of unresolved targets [6]. Thus, the wideband radar can improve target detection performance compared to a narrowband radar.

Over the past few decades, many detectors for distributed targets have been proposed with various expressions based on different signals or clutter models. In particular, the radar detection of distributed targets in white Gaussian noise with a priori knowledge of the spatial distribution has been addressed [1]. Therein, the spatial scattering density generalized likelihood ratio test (GLRT) has been proposed and analyzed. In addition, an adaptive detection of a range-spread target embedded in Gaussian noise with an unknown covariance matrix has been discussed [7]. The detector proposed in Ref. [7] relies on a modified GLRT design procedure and does not resort to secondary data.

This detector, however, is dependent on the covariance matrix; hence, it does not ensure the constant false alarm rate (CFAR) property. The detection of a range-spread target modeled as a multirank random Gaussian signal in an unknown Gaussian disturbance has been addressed [8]. In addition, detectors of a range-spread target in the presence of noise and subspace interference have been addressed [9]. And the fluctuating target detectors have been designed in non-Gaussian clutter [10, 11].

Most of the aforementioned methods assume a homogeneous environment, i.e., the detection samples share the same covariance matrix as the reference cells. However, the assumption of a homogeneous environment is rather idealistic and inappropriate for modeling wideband radar clutter [12, 13], and the partially homogeneous model is sufficient to describe the clutter for radar with a high range resolution. The partially homogeneous clutter assumes that the detection (primary) and reference (secondary) data share the same structure, but the power levels are different from each other. Rao and Wald tests for distributed targets in partially homogeneous environment have been proposed and analyzed [14–16]. By modeling the disturbance as an autoregressive process, parametric Rao tests have also been developed [17, 18]. Moreover, an adaptive detection method of distributed targets without secondary data has been proposed based on a Bayesian approach [19]. However, the assumption in this method is not always realistic because the scattering geometry is different from each other. GLRT, Rao test, and Wald test have been analyzed in a heterogeneous environment based on a knowledge-aided Bayesian approach [20]. Additionally, range spread targets detectors based on time–frequency analysis technology have been designed [21], which can achieve good performance but is time consuming and challenging to materialize. In addition, distributed targets detection methods, which do not require secondary data but assume the inverse covariance structure of the interference defined via unitary invariant functions, have been developed resorting to advanced convex optimization strategies [22]. The methods mentioned earlier, however, often assume that the targets do not have range walking across the range cells in a coherent processing interval (CPI). Nevertheless, the target range walking during a CPI is generally larger than one range cell for wideband radar and cannot be neglected. GLRT-based detectors have been proposed in the range frequency domain with the range walking effect, but the detectors have high computational complexity and poor performance [23].

In our conference paper [24], we have presented the range frequency domain-Rao (RFD-Rao) test for range spread targets with range walking, but the performance has not been discussed in detail. Herein, we present more details regarding the RFD-Rao detector, and propose the range frequency domain-Wald (RFD-Wald) detector. In addition, the detection performance of the proposed RFD-Rao and RFD-Wald tests are discussed herein. It is shown that these two detectors are independent of the unknown parameters in the null hypothesis, which results in the CFAR property. Comparisons between the two new detectors and the existing detectors show that our RFD-Rao test exhibits improved detection performance with limited training data, and the two detectors have the same performance in the asymptotic case.

The remainder of the paper is organized as follows: Section 2 describes the detection problem, and establishes the target return model and the clutter model in the range frequency domain. Section 3 expresses the detection problem based on the Neyman–Pearson criterion and designs the RFD-Rao and RFD-Wald detectors. Section 4 analyzes the statistical properties of the proposed detectors, and Section 5 presents the performance assessment of the proposed methods with Monte–Carlo tests. Finally, Section 6 offers some concluding remarks and hints for future research.

2 Problem formulation and signal model

2.1 Target return model

Suppose that a train of coherent wideband linear frequency modulated (LFM) signal is transmitted by a wideband radar and M pulses exist in a CPI. If a target occupies L contiguous range cells, the output of the matched filter after a range compression in the discrete slow time-range frequency domain can be denoted as

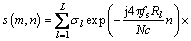
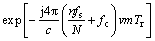           (1)

where m=1, …, M is the number of pulses, n=1, …, N, where N is the sample number of the discrete frequency spectrum, σ_l is a complex number related to the scattering coefficient in the lth range cell, v is the radial velocity of the target, c is the light speed, R_l is the radial range of the lth range cell, T_r is the pulse repetition period, f_c is the carrier frequency of the radar, and f_s is the sampling rate. The preceding model implies an assumption that the targets scattering in each range cell are invariant in amplitude, initial phase, and radial velocity during a CPI, and the target has only translational motion. It is worth noting that the target length is unknown, and the target may have range migration during a CPI. Thus, the length of the detection window should be set sufficiently long to include all target returns and longer than the target size, i.e., N>L. In addition, the target radial velocity is considered as a known parameter herein. In practice, it can be estimated before target detection. The target return vector in the nth range frequency bin can be denoted as

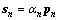                               (2)

where 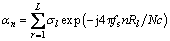and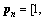 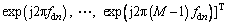are the complex amplitude of the target and the Doppler steering vector in the nth range frequency bin, respectively, with [·]^T denoting vector transposition. The normalized Doppler frequency in the nth range frequency bin can be written as

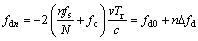            (3)

where 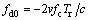is the Doppler frequency of the first range frequency bin and 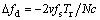is the difference in the Doppler frequencies between two adjacent range frequency bins.

2.2 Clutter model

In this work, partially homogenous zero-mean Gaussian vectors are used as the range frequency domain clutter model. Without loss of generality, it is assumed that the primary data originate from the first N range cells and the secondary data from the next K range cells. The primary clutter data in the range frequency domain can be obtained by applying the discrete Fourier transform (DFT) to each row of the time-domain clutter matrix, and denoted as a matrix 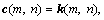where n=1, …, N and m=1, …, M. Similarly, the secondary clutter data in the range frequency domain can be denoted as a matrix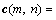 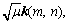where n=N+1, …, N+K, m=1, …, M, and μ is a nonnegative random variable accounting for the clutter power of the secondary data. The clutter power of the primary data is regarded as 1. The column vectors k(·, n) are independent M-dimensional zero-mean complex Gaussian random vectors with a normalized covariance matrix R=E{k(·,n)k^H(·, n)}, where [·]^H represents conjugate transposition. It has been proven that the clutter vectors in all range frequency bins have the same covariance as the clutter vectors in all range cells [23]. Thus, the clutter in the range frequency domain can also be considered as partially homogenous clutter. The covariance matrixes of the clutter in the range frequency domain are given by

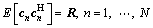                  (4)

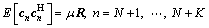          (5)

where c_n=c(·, n).

2.3 Detection problem description

With the target return and clutter models mentioned above, the detection problem can be formulated in terms of the following binary hypotheses test:

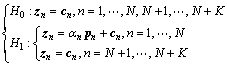        (6)

where z_n is the observed vector in the nth range frequency bin, and c_n is the zero-mean Gaussian random vector in the range frequency domain, which represents the clutter plus noise. Herein, the clutter is dominant against the noise, and partially homogeneous clutter is considered. The secondary data does not contain any useful target signals.

To evaluate the test statistics, we denote the primary and secondary data matrices by Z_N=[z₁, …, z_N] and Z_K=[z_N+1, …, z_N+K], respectively. Z=[Z_N Z_K] is the full data matrix, and θ_r=[α_1,R, α_1,I, …, α_N,R, α_N,I]^T is a 2N-dimensional real column vector, where α_n,R and α_n,I are the real and imaginary parts of α_n, respectively. In addition, α=diag(α₁, …, α_N), where diag(α₁, …, α_N) is the N×N diagonal matrix whose diagonal entries are α₁, …, α_N. Further, θ_s=[μvec(R)]^T is an (M²+1) dimensional real column vector of nuisance parameters, where vec(·) denotes the vectorization operation. θ=[θ_r, θ_s] is an (M²+2N+1)-dimensional real column vector, and P=[p₁, …, p_N] is the steering matrix.

3 Detector design

With the target model and clutter model mentioned above, the RFD-Rao and RFD-Wald detectors are proposed herein. It is worth noting that the proposed detectors are different from the detectors in Refs. [15, 25], the authors of which designed adaptive Rao and Wald tests for distributed targets in the time domain without range walking effects, while the range walking effects are considered and the detectors are designed in the range frequency domain in this work. Hereafter, the data Z are discussed as in the range frequency domain rather than in the time domain.

3.1 RFD-Rao test design

The RFD-Rao test can be expressed as [15]

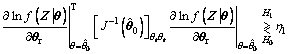(7)

where (·)/θ_r denotes the gradient operator with respect to θ_r, η₁ is the detection threshold of the RFD-Rao test according to the desired value of the false alarm probability (P_f); J(θ) is the Fisher information matrix (FIM) and can be partitioned into four parts:

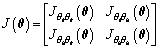                 (8)

f(Z|θ) is the probability density function (PDF) of the data under H₁, and can be written as [25]

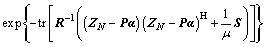(9)

where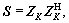||·|| and tr(·) denote the determinant and trace of the argument, respectively. 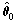is the maximum likelihood estimate (MLE) of θ under the H₀ hypothesis.

The inverse of the Fisher information matrix with respect to θ_r can be derived as [15]

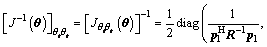
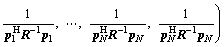(10)

and the following can be easily obtained:

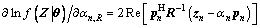   (11)

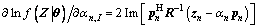   (12)

where Re[·] and Im[·] denote the real and imaginary part of the argument, respectively.

As shown in Ref. [3], we have

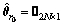                              (13)

where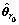is the MLE of θ_r under the H₀ hypothesis. Substituting Eqs. (8)–(13) into Eq. (7), the following can be derived after some algebraic manipulations:

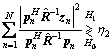                       (14)

where |·| denotes the modulus of a complex number and η₂ is the appropriate modification of the original threshold in Eq. (7).

Let 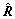be the MLE of R under the H₀ hypothesis; therefore, it can be written as

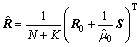                   (15)

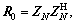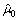where and is the unique position solution of the equation [25]

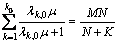                      (16)

where k₀=min(M, N), and the λ_k,0, k=1, …, k₀, are the nonzero eigenvalues of the matrix S^–1/2R₀S^–1/2. Substituting Eq. (15) into Eq. (14) yields

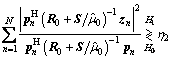               (17)

3.2 RFD-Wald test design

The RFD-Wald test can be expressed as [15]

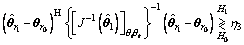     (18)

where η₃ is the detection threshold of the RFD- Wald test, 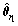is the MLE of θ_r under the H₁ hypothesis, and θ_r0 is the value of θ_r under the H₀ hypothesis. Therefore, the following can be obtained:

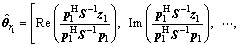
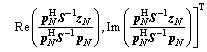        (19)

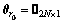                             (20)

Further, the MLE of R under the H₁ hypothesis is

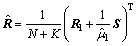                   (21)

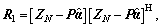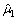whereandis the unique position solution of the Eq. [25].

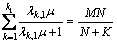                      (22)

where k₁=min(M–1, N), and the λ_k,1, k=1, …, k₁, are the nonzero eigenvalues of the matrix S^–1/2R₁S^–1/2.

Substituting Eqs. (19)–(21) into Eq. (18), we obtain the following decision after some algebra manipulations:

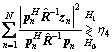                       (23)

where η₄ is the appropriate modification of η₃ in Eq. (18).

With the well-known matrix inversion lemma, we can obtain [25]

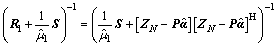
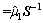                              (24)

Substituting Eq. (24) into Eq. (23) yields

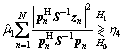                     (25)

4 Performance analyses

4.1 CFAR of RFD-Rao and RFD-Wald tests

First, the CFAR property of the designed tests is analyzed. For a given μ=1, Eq. (17) becomes the RFD-Rao test in homogeneous environments, and this test can be obtained through a two-step GLRT design criterion in the range frequency domain, where the clutter covariance matrix is estimated with both the primary and secondary data. When μ=1, detector (25) reduces to the general adaptive matched filter (GAMF) test [3] in the frequency domain.

Remarkably, the proposed RFD-Rao and RFD-Wald tests possess the desired CFAR property with respect to the clutter power μ and to the covariance matrix R, although closed-form expressions for the false alarm probability cannot be obtained except for μ=1. The detailed proof is shown in the appendix.

4.2 Asymptotic false alarm and detection performance

Next, we analyze the asymptotic performance of the detectors. According to Ref. [26], both the Rao and the Wald tests share the same asymptotic (chi squares) distribution. Similarly, the proposed RFD-Rao and RFD-Wald test statistics also asymptotically obey the chi-square distribution, and can be expressed as

               (26)

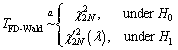              (27)

where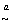means the statistic asymptotically obeys a certain probability distribution,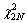is the central chi-squared distribution with 2N degrees of freedom, and 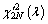is the noncentral chi- squared distribution with 2N degrees of freedom. The noncentrality parameter λ can be expressed as

λ=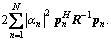 It is worth noting that λ is related to the signal-to-clutter-plus-noise ratio (SCNR, R_SCN) at the output of the whitening filter, and these two detectors show the same asymptotic performance, which is confirmed in the simulation results reported in the next section. For a given threshold γ, the asymptotic probability of a false alarm can be written as

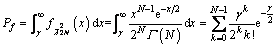(28)

where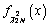denotes the PDF of a 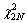random variable, and Γ(·) is the gamma function. Further, Eq. (28) can be easily inverted to obtain the test threshold γ for a given P_f. In addition, the detection probability (P_d) is given by

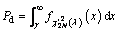
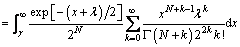   (29)

for a given test threshold γ, where 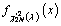denotes the PDF of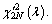

5 Numerical results

In this section, we present some numerical examples to assess the detection performance of the proposed detectors. In addition, we compare our detectors to the range frequency domain-general adaptive subspace detector (FD-GASD) test proposed [23]. Additionally, the optimum but nonadaptive detector is included as the benchmark in each case (it is worth noting that the optimal test is a detector that has full knowledge of all unknown parameters, i.e., the clutter power level and covariance matrix in the frequency domain).

5.1 Simulation settings

The performance assessment is performed with Monte–Carlo simulations to estimate the detection probability. To eliminate random effects upon the simulation results of the detection probabilities, the number of Monte–Carlo trials used to estimate the values of P_d is 5000, and 100/P_fa times of independent trials are conducted to determine the false alarm probability. Consequently, P_fa is set as 10^–3 for all simulations throughout this section to decrease the computational burden.

We assume that the radar transmits a train of LFM pulses and that eight pulses exist in a CPI. The radar carrier frequency f_c=10 GHz, bandwidth B=100 MHz, and PRF=500 Hz. The returns of the target span four range cells, and the complex amplitude of each scatter of the target is modeled as a Rayleigh fluctuating random variable. The maximum radial velocity of the target is 375 m/s, and thus the target walks at most four range cells during a CPI. The detection window consists of eight consecutive range cells to containing all target returns.

The SCNR is defined as R_SCN= 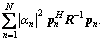As for the clutter, it is modeled as an exponentially correlated complex normal vector with a one-lag correlation coefficient ρ, i.e., the (i, j)th element of the covariance matrix R is given by ρ^|i–j|, with ρ=0.9.

5.2 Influence of range walking

In the first simulation, we consider the influence of range walking across the range cells on the proposed detectors. For our detectors, range walking is considered in the modeling target returns. Subsequently, we compare our algorithms with the united Doppler steering vector-general adaptive subspace detector (USV-GASD) [23], in which the range walking across the range cells is ignored and all range frequency bins are assumed to share the same Doppler frequency, i.e., f_dn=f_d0. Their performance curves are shown in Figure 1 for K= 32, v=100 m/s, and μ=10. The figure shows that the RFD-Rao test is worse than the optimal test by approximately 2 dB, and the proposed RFD-Rao and RFD-Wald tests outperform the FD-GASD by approximately 0.7 dB and 0.2 dB, respectively. The performance of the USV-GASD test, however, is much worse than the other four tests. This is because the target return model in the USV-GASD mismatches the true target returns, causing the detector unable to coherently integrate the energy of the target returns, thus incurring a significant degradation in the detection performance.

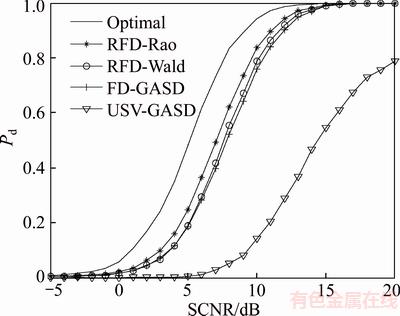
Figure 1 Detection probabilities of RFD-Rao, RFD- Wald, FD-GASD, and USV-GASD vs SCNR for M=8, N=8, K=32, v=100 m/s and μ=10

5.3 Effect of number of secondary data

Next, we examine the effect of the sample number of the secondary data on the detection performance. Numerical simulations are provided for various values of K and μ when M=8. In particular, we consider two distinct cases: 1) the limited-training case, e.g., K=32 and K=48; and 2) the asymptotic case, e.g., K=256. The simulation results are shown in terms of the detection probabilities versus the SCNR. It is worth noting that the performance of the USV-GASD is poor, and we primarily focus on the detection performance of the proposed detectors; the performance curve of the USV-GASD is ignored in the following simulations.

First, we discuss the limited-training case. For K=32, Figures 2(a) and (b) show the detection probabilities versus SCNR for μ=10 and μ=2, respectively. The figures highlight that, in these two cases, the RFD-Rao test generally yields the best performance among the adaptive detectors, while the FD-GASD and RFD-Wald detectors achieve almost the same detection performance. This is because the RFD-Rao utilizes both the primary and secondary data for the covariance matrix estimation, while the FD-GASD and RFD-Wald tests use only the secondary data. Additionally, the proposed tests have almost the same detection performance, even for a large value of μ=10, as shown in Figure 2(a) or for a small value of μ=2 in Figure 2(b), indicating that the detectors are robust to the power scaling factor μ.

In the second case with K=48, the simulation results are plotted in Figure 3 for μ=10. The figure shows that the RFD-Rao test still has the best performance among the adaptive detectors, and the RFD-Wald detector achieves a better detection performance than the FD-GASD test. In addition, all of these detectors have better performance than the K=32 case in Figure 2(a), which indicates that the proposed detectors have better performance with the increase in the sample number K.

In Figure 4, an asymptotic scenario with a large K is simulated to verify the asymptotic performance of the tests derived in section 4. Further, the performance of the FD-GASD detector is included for comparison. In this case, we assume that K=256 is sufficiently large to simulate the asymptotic case. The simulation parameters are M=8, N=8, v=375 m/s and μ=10. The results highlight that the detection probabilities approach the asymptotic performance of the optimal test when the sample number of the secondary data is sufficiently large. Moreover, although the proposed RFD-Wald test shows poor performance in the limited training case, it provides almost the same detection performance as the RFD-Rao test in the asymptotic scenario, which accords with the theoretical analysis.

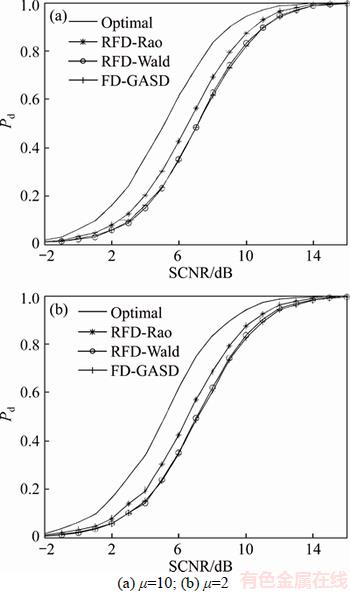
Figure 2 Detection probabilities vs SCNR for M=8, N=8, K=32 and v=375 m/s:

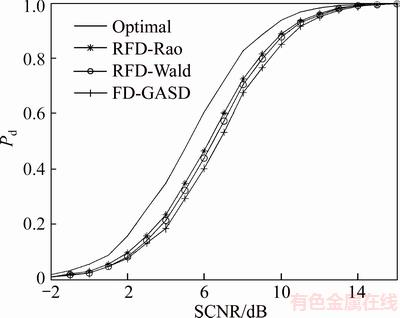
Figure 3 Detection probabilities vs SCNR for M=8, N=8, K=48, v=375 m/s and μ=10

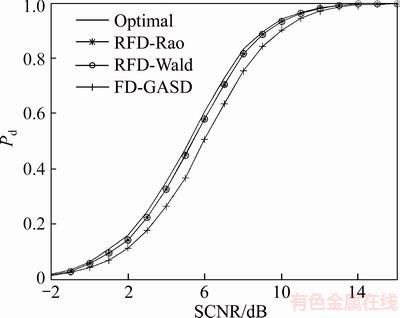
Figure 4 Detection probabilities vs SCNR for M=8, N=8, K=256, v=375 m/s and μ=10

5.4 Influence of target velocity

In the following, we illustrate the relationship between the target radial velocity and the performance of the RFD-Rao and RFD-Wald detectors. In Figure 5, the performance curves of the RFD-Rao and RFD-Wald are shown respectively when the target radial velocities are 50, 200 and 375 m/s for K=32 and μ=10. The curves show that the detection performance of the designed tests varies with the target radial velocity. It is worth noting that the tests have better performance with the increase in the target radial velocity. This is because the increase in the target velocity can result in a decrease in the detection threshold for a determined P_f when the number of secondary data is limited.

6 Conclusions

Herein, the problem of detecting distributed targets with range walking across range cells in a coherent processing interval in a partially homogeneous clutter has been analyzed. Based on the target return and clutter model, two novel adaptive distributed targets detectors, the RFD-Rao and RFD-Wald, have been designed. Furthermore, the statistical properties of the two new detectors have been analyzed in detail. Interestingly, the proposed detectors ensure the CFAR property with respect to both the clutter covariance matrix and the power level. Additionally, the asymptotic performance of these detectors is also analyzed and these two detectors show the same asymptotic performance. Finally, the performance assessment, conducted via Monte–Carlo simulations, shows the effectiveness of the proposed detection algorithms. More precisely, the proposed two detectors show better performance than the USV-GASD detector, which ignores the range walking effect. The RFD-Rao detector outperforms the RFD-Wald and FD-GASD detectors when the secondary data are limited and the proposed detectors have better performance with the increase in the secondary data. The detection performance of the designed tests becomes better with the increase in the target velocity. The analysis of the proposed detectors in a heterogeneous environment is our future research.

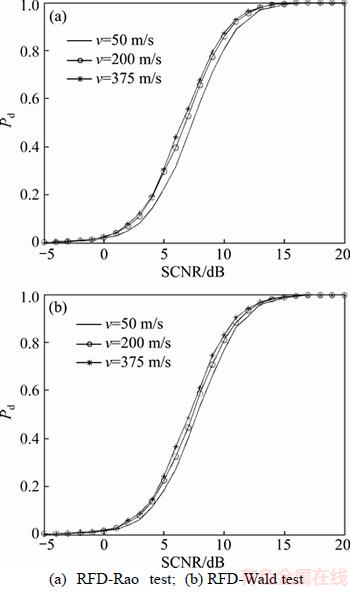
Figure 5 Detection probabilities of RFD-Rao and RFD-Wald vs SCNR in case of v= 50, 200 and 375 m/s for M=8, N=8, K=32 and μ=10:

Appendix

CFAR of RFD-Rao and RFD-Wald tests

We used an analysis method similar to those in Refs. [6, 23] to verify the CFAR property of the proposed methods. First, we recast the tests using Eqs. (17) and (25) for a more convenient form. 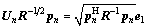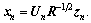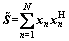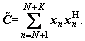Hence, we denote by U_n the unitary transformation aimed at rotating each whitened steering vectors R^–1/2p_n onto the direction of e₁=(1, 0, …, 0), and by x_n, n=1, …, N+K the transformed whitened data vectors, i.e., and Let S and C be the sample covariance matrix of the transformed primary and secondary data, respectively, i.e.,and The RFD-Rao and RFD-Wald tests in Eqs. (17) and (25) can be rewritten as

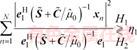                   ⁽³⁰⁾

and

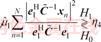                        ⁽³¹⁾

where μ₀ is the solution of the equation

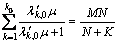                      (32)

where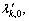 k=1, …, k₀ are the nonzero eigenvalues of the matrix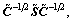 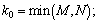μ₁ is the unique position solution of the following equation:

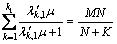                      (33)

where 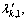k=1, …, k₁, denote the nonzero eigenvalues of the matrix 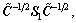k₁=min(M–1, N), and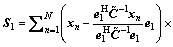

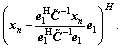
Further, x_n, n=1, …, N and x_n, n=N+1, …, N+K are independent, zero-mean, complex Gaussian vectors, with covariance matrices I_M and μI_M, respectively, where I_M denotes the M×M identity matrix. In addition, the solution of Eq. (32) can be recast as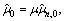where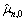is the solution of Eq. (33) with 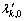substituted by 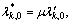k=1, …, k₀, and is independent of either R and μ; the solution of Eq. (33) can be recast as 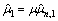, where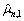is the solution of Eq. (33) with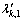substituted by 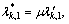k=1, …, k₁, and is independent of either R and μ.With these conclusions, it is obvious that detectors (17) and (25) have CFAR properties with respect to R and μ under the H₀ hypothesis.

References

[1] GERLACH K, STEINER M. Detection of a spatially distributed target in white noise [J]. IEEE Signal Processing Lett, 1997, 4(7): 198–200.

[2] GERLACH K. Spatially distributed target detection in non-Gaussian clutter [J]. IEEE Trans on Aerosp Electron Syst, 1999, 35(3): 926–934.

[3] CIUONZO D, MAIO A D, ORLANDO D. A unifying framework for adaptive radar detection in homogeneous plus structured interference–part I: On the maximal invariant statistic [J]. IEEE Trans on Signal Processing, 2016, 64(11): 2894–2906.

[4] MOYA J C, MAIO A D, MENOYO J G, LOPEZ A A. Experimental performance analysis of distributed target coherent radar detectors [J]. IEEE Trans on Aerosp Electron Syst, 2012, 48(3): 2216–2238.

[5] SUN Xin, LU Bi-ying, JIN Tian, ZHOU Zhi-min. Antenna planes based wall-clutter mitigation in through-wall-imaging applications [J]. Journal of Central South University, 2016, 23(10): 2638–2646.

[6] CONTE E, MAIO A D, RICCI G. GLRT-based adaptive detection algorithms for range-spread targets [J]. IEEE Trans on Signal Processing, 2001, 49(7): 1336–1348.

[7] GERLACH K, STEINER M. Adaptive detection of range distributed targets [J]. IEEE Trans on Signal Processing, 1999, 47(7): 1844–1851.

[8] JIN Y, FRIEDLANDER B. A CFAR adaptive subspace detector for second-order Gaussian signals [J]. IEEE Trans on Signal Processing, 2005, 53(3): 871–884.

[9] BANDIERA F, MAIO A D, GRECO A S, RICCI G. Adaptive radar detection of distributed targets in homogeneous and partially homogeneous noise plus subspace interference [J]. IEEE Trans on Signal Processing, 2007, 55(4): 1223–1237.

[10] LIU Jun, ZHANG Zi-jing, CAO Yun-he, WANG Min. Distributed target detection in subspace interference plus Gaussian noise [J]. Signal Processing, 2014, 95: 88–100.

[11] KAFSHGARI S, MOHSENI R. Fluctuating target detection in presence of non Gaussian clutter in OFDM radars [J]. Int J Electron Commun, 2013, 67: 885–893.

[12] MELVIN W L. Space-time adaptive radar performance in heterogeneous clutter [J]. IEEE Trans on Aerosp Electron Syst, 2000, 36(2): 621–633.

[13] WU Ren-biao, SU Zhi-gang, WANG Lu. Space-time adaptive monopulse processing for airborne radar in non-homogeneous environments [J]. Int J Electron Commun, 2011, 65: 258–264.

[14] MAIO A D, IOMMELLI S. Coincidence of the Rao test, Wald test, and GLRT in partially homogeneous environment [J]. IEEE Signal Processing Lett, 2008, 15: 385–388.

[15] CONTE E, MAIO A D. Distributed target detection in compound-Gaussian noise with Rao and Wald tests [J]. IEEE Trans on Aerosp Electron Syst, 2003, 39(2): 568–581.

[16] LIU Wei-jian, XIE Wen-chong, WANG Yong-liang. Rao and Wald tests for distributed targets detection with unknown signal steering [J]. IEEE Signal Processing Lett, 2013, 20(11): 1086–1089.

[17] WANG Pu, LI Hong-bin, HIMED B. Generalized parametric Rao test for multi-channel adaptive detection of range spread targets [J]. IET Signal Processing, 2012, 6(5): 404–412.

[18] SHI Bo, HAO Cheng-peng, HOU Chao-huan, MA Xiao- chuan, PENG Cheng-yan. Parametric Rao test for multichannel adaptive detection of range-spread target in partially homogeneous environments [J]. Signal Processing, 2015, 108: 421–429.

[19] BANDIERA F, BESSON O, RICCI G. Adaptive detection of distributed targets in compound-Gaussian noise without secondary data: a Bayesian approach [J]. IEEE Trans on Signal Processing, 2011, 59(12): 5698–5708.

[20] ZHOU Yu, ZHANG Lin-Rang. Knowledge-aided Bayesian radar adaptive detection in heterogeneous environment: GLRT, Rao and Wald tests [J]. Int J Electron Commun, 2012, 66: 239–243.

[21] XU Shu-wen, SHUI Peng-lang. Range-spread target detection using 2D non-local nonlinear shrinkage map [J]. Signal Processing, 2014, 98: 337–343.

[22] AUBRY A, MAIO A D, PALLOTTA L, FARINA A. Radar detection of distributed targets in homogeneous interference whose inverse covariance structure is defined via unitary invariant functions [J]. IEEE on Trans Signal Processing, 2013, 61(20): 4949–4961.

[23] DAI Feng-zhou, LIU Hong-wei, SHUI Peng-lang, WU Shun-jun. Adaptive detection of wideband radar range spread targets with range walking in clutter [J]. IEEE Trans on Aerosp Electron Syst, 2012, 48(3): 2052–2064.

[24] WANG Yu, CAO Yun-he, SU Hong-tao, WANG Sheng-hua. Adaptive Rao detector for distributed targets in the frequency domain [C]// IET International Radar Conference 2015, 2015: 1–4.

[25] HAO Cheng-peng, MA Xiao-chuan, SHANG Xiu-qin, CAI Long. Adaptive detection of distributed targets in partially homogeneous environment with Rao and Wald tests [J]. Signal Processing, 2012, 92(2012): 926–930.

[26] KAY S M. Fundamentals of statistical signal processing detection theory [M]. Englewood Cliffs, NJ: Prentice-Hall, 1998.

(Edited by FANG Jing-hua)

中文导读

具有距离走动效应的RFD-Rao和RFD-Wald分布式目标检测器

摘要：提出两种新型自适应分布式目标检测器：距离频域Rao(RFD-Rao)和距离频域Wald(RFD-Wald)检测器。 该方法考虑相参处理间隔（CPI）内部分均匀干扰环境和目标距离走动效应的影响，分析检测器的渐近性能，并给出不同杂波协方差矩阵和功率水平下的恒虚警率（CFAR）特性分析。将本文所提出的自适应检测器的性能通过蒙特卡罗试验进行了验证，仿真结果证明所提出的检测算法与现有的类似检测器相比的有效性。

关键词：自适应检测；分布式目标；Rao检测器；Wald检测器；距离走动

Foundation item: Project(61771367) supported by the National Natural Science Foundation of China

Received date: 2017-01-06; Accepted date: 2017-04-05

Corresponding author: CAO Yun-he, PhD, Professor; Tel: +86–29–88202350; E-mail: cyh_xidian@163.com; ORCID: 0000-0002- 0430-2976