岩石钻掘过程中的钻头温度分析

杨晓峰，李晓红，卢义玉

(重庆大学 西南资源开发及环境灾害控制工程教育部重点实验室，重庆，400030)

摘要：为深入研究钻头钻掘岩石过程中的温度变化规律，通过对钻头钻掘岩石的传热过程分析，建立描述钻头在钻掘岩石过程中温度变化的微分方程组，归纳影响钻头温度变化的各种影响因素。在对钻头钻掘岩石过程进行热功转换分析的基础上，给出钻头温度的解析计算方法，并结合钻头切削面温度解析计算式，给出钻头温度的解析方程。研究结果表明：钻头在钻掘岩石过程中的温度受几何条件、热物性质、钻掘参数等因素影响；在其他条件一定的情况下，钻头平均温度升高与钻头推进速度v的平方根成正比。

关键词：岩石；钻掘；侵入；切削；温度

中图分类号：TD80          文献标志码：A         文章编号：1672-7207(2011)10-3164-06

Temperature analysis of drill bit in rock drilling

YANG Xiao-feng, LI Xiao-hong, LU Yi-yu

(Key Laboratory for the Exploitation of Southwestern Resources and the Environmental Disaster Control Engineering,

Ministry of Education, Chongqing University, Chongqing 400030, China)

Abstract: Temperature variation of the drill bit in the process of rock drilling was studied systematically. Through the analysis of heat transfer process of the drilling in rock drilling, differential equations which described the temperature fluctuations in the process of rock drilling were established and various factors which affected the temperature fluctuations of the drill bit were also analyzed. Based on the analysis of the conversion between thermal and power in rock drilling, analytical method for temperature computation of the drill bit was given. Analytical equation of the bit temperature was derived associated with the analytical expression of cutting temperature. The results show that the temperature of drill bit is influenced by geometry condition, thermal properties, drilling element, and so on. The average rising temperature is proportional to the square root of forward speed v of the drill bit when the other conditions remain unchanged.

Key words: rock; drill; penetration; cutting; temperature

在地质勘探、矿山开采、石油钻井等领域，经常需要钻掘坚硬岩层。钻头在钻掘岩石过程中会出现明显的温度升高现象。温度过高不但会使钻头产生的热应力超出钻头材料的许用强度，还会产生材料变性等不利影响，使钻头使用寿命下降，过早失效^[1-2]。分析钻头温度变化的影响因素，深入研究钻头温度变化规律，对全面探索钻头破损机理和提高钻头使用寿命有很强的实用价值。在钻头破碎硬岩石过程中，绝大部分切削功将会转化为切削热，致使钻头的温度迅速升高。Beste等^[3]估计一般情况下钻头的平均工作温度为500 ℃左右，但是，Jorn^[4]研究钻头工作后的表面时发现存在一些高温形成相，某些相点显示其工作中的瞬时温度超过1 000 ℃。李晓红等^[5]也指出温度升高造成的热破坏是岩石切削过程中刀具的主要破坏因   素^[5]。然而，由于工作条件恶劣和影响因素复杂，关于岩石钻掘过程的钻头温度具体的计算方法至今尚未见报道。在此，本文作者借助微分方程对钻头在钻掘岩石中的热量传递过程进行分析，归纳出影响钻头温度变化的各种因素；在热功转换分析的基础上给出钻头温度解析计算模型并分析钻头温度变化的规律，以便为钻头失效机理的深入研究和工程应用提供参考 依据。

1  岩石钻掘过程中的钻头温度

1.1  钻头-岩石-切屑系统的传热分析

钻头的温度与岩石及其切屑密切相关，要准确描述钻头的温度就必须把另外两者的影响因素也予以考虑。在研究过程中，可以把钻头、岩石、岩石切屑看成一个封闭的热力学系统，热量的传递只在这三者之间发生。

假设剪切热只在剪切变形区产生，在未破坏区域不存在内部发热源。未发生剪切破坏区的岩石温度控制方程为^[6-7]：

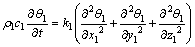     (1)

式中：ρ₁为岩石的密度；c₁为岩石的比热容；k₁为岩石的导热系数；(x₁，y₁，z₁)为岩石内任一点坐标；t为时间变量；θ₁为对应点岩石温度。在发生剪切变形造成破坏的岩石切屑区域，其温度控制微分方程为：

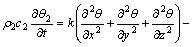
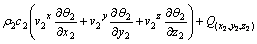  (2)

式中：ρ₂为岩石的密度；c₂为岩石的比热容；k₂为岩石的导热系数；(x₂，y₂，z₂)为任一点岩石切屑的坐标；t为时间变量；θ₂为对应点切屑温度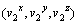；为该点剪切变形速度在各方向上的速度分量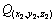；为(x₂，y₂，z₂)处产生的剪切热。

对于旋转推进的钻头，其温度微分控制方程为：

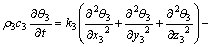
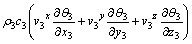      (3)

式中：ρ₃为钻头材料的密度；c₃为钻头材料的比热容；k₃为钻头材料的导热系数；(x_i，y_i，z_i)为钻头内任一点坐标；θ₃为对应点钻头温度；t为时间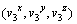；为对应点在各方向上的速度分量。

可以看出，式(1)~(3)的求解必须满足许多条件，主要包括：

(1) 几何条件，即参与发热、传热过程所有物体的形状和尺寸，如岩石、刀具、岩石切屑的形状和    尺寸。

(2) 物理条件，即需要确定各相关物性量(岩石、切屑、刀具的密度、比热容、导热系数等)、内热源大小和分布等。

(3) 时间条件，即确定过程在时间变化上的特点(包括这些物性量随温度变化的函数关系等)。

(4) 边界条件，即需要定义区域边界上的输入  条件。

(5) 剪切区材料在任意点的变形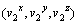速度和刀具速度。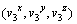

(6) 剪切变形发热量Q的分布情况。

该微分方程组系统反映了钻头温度的各种影响因素。尽管利用该方程组对某点温度进行预测，但是，由于求解过程中所需条件太多，温度随影响因素的变化趋势不容易掌握。

不用数值计算而是用解析的方法求解上述微分方程，而且能用含有切削各要素的函数解析式来表示温度(某特定点或特定区域的温度如接触面的平均温度)，就可以知道切削温度随各主要切削要素的变化规律，从而得知切削温度变化的一般规律。采用解析解法求解不但有利于人们了解问题本质，而且可以更直观和方便地指导工程应用。

1.2  钻头温度的解析法求解

钻头对岩石的钻掘可以划分为推力作用下钻头前端部对的岩石压入和扭矩作用下侧端面对岩石的旋转切削，即轴向的推进和径向的旋转2个过程，如图1所示。

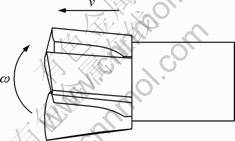
图1  钻头钻掘过程主要运动示意图

Fig.1  Schematic diagram of major movements of drill bit in process of rock drilling

对于每个刀齿，其前端面在推力作用下压入岩石一定深度，然后侧端面在扭矩作用下旋转，切削周围岩石，实现对岩石材料的去除。从能量角度分析，切削力和推力都做功，两者都致使钻头温度升高。每个过程的主要热源有2个：岩石在刀具力作用下剪切破坏产生的剪切发热，岩石及其切屑与刀具摩擦产生的热量。

1.2.1  推力作用下的压入面温度解析方程

钻头前端面在推力作用下压入岩石，可以看成压头侵入岩石过程。本文采用压剪破碎理论建立岩石侵入破裂的过程模型：岩石按摩尔破坏条件在剪切面上发生剪切破坏^[8]，破坏后的岩石碎屑沿刀片端面流出(如图2所示)。使钻头温度升高的热源主要有2个：岩石剪切变形热和刀屑间的摩擦热。

图2  岩石侵入破裂示意图

Fig.2  Schematic diagram of penetrated fracture of rock

根据Bever等^[9]的研究和实验结果，固体切割破碎时所有与切屑形成有关系的能量几乎完全被转化为热能，而形成新表面的表面能相对于热能来说可以忽略。根据Jaeger等^[10-11]的分析和实验结果，可以近似认为侵入破碎产生的热量在工作面上均匀分布。

(1) 压入过程剪切热致温升计算。单位时间、单位面积在岩石剪切面上产生的剪切热q₁为：

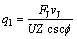             (4)

式中：v_J为剪切速度；F_J为剪切力；U为压入刃宽度；Z为剪切厚度。设剪切热流入刀具的比率为R₁，则流入切屑的比率为(1-R₁)，根据比热容公式，剪切面的平均温度升高θ_J应为：

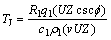           (5)

根据Weiner给出的剪切面热量分布模型，热量分配比率R₁可按下式计算^[12]：

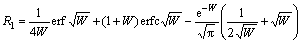(6)

式中：erf(W)为关于W的误差函数；erfc(W)为误差函数的余函数；W为计算参数。

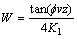             (7)

式中：K₁为岩石的导温系数。

(2) 压入过程摩擦热致温升计算。单位时间、单位面积在摩擦面上产生的摩擦热q₂为：

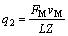             (8)

式中：v_M为摩擦速度；F_M为摩擦力；L为岩石与钻头端面的摩擦接触长度。设R₂是摩擦热传入钻头的比率，则流入切屑中的摩擦热为(1-R₂)q₂。岩石切屑与刀具间摩擦运动可根据Jeager提出的移动摩擦表面与平面作用模型计算^[9]，则由摩擦造成的切屑表面平均温度升高?θ_M为：

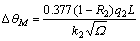         (9)

式中：k₂为岩石切屑的导热系数；Ω为计算参数，

式中：K₂为岩石切屑的导温系数。综合前面分析，侵入岩石的钻头前端面平均温度升高T_T为：

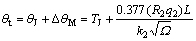
为解出未知数R₂还要从钻头的角度求出θ_T。刚压碎的岩屑与钻头端面紧密接触，可以看成固定的连续摩擦热源，参考Jeager给出的计算方法^[10]，钻头端面接触区的平均温升应为：

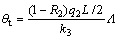         (10)

式中：k₃为刀具材料的导热系数；Λ为移动平面热源的形状系数^[11]。根据Blok温度法则^[13]，两摩擦面在接触区域的平均温度应该相等，故联立式(9)和(10)，解热量分配比率R₂：

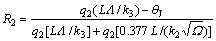    (11)

将式(12)代入式(9)，则由摩擦造成的平均温升为：

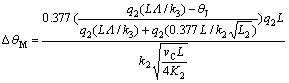(12)

(3) 计算参数的确定。在已知推力P和推进速度v的情况下，求解式(13)还需对岩石压入过程中的剪切力F_J和剪切速度v_J、摩擦力F_M和摩擦速度v_M等参数进行求解。对钻头压入前端面在推力作用下侵入岩石过程进行受力分析，如图3所示。

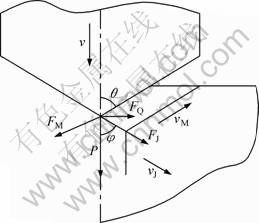
图3  岩石侵入受力示意图

Fig.3  Schematic diagram of force in penetrated fracture of rock

若端面的锥角为2θ，则在端面与岩石的接触部，端面上正应力合力F_nc应为^[14]：

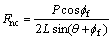           (13)

则端面上摩擦力合力应为：

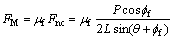       (14)

式中：μ_f为钻头与岩石间的摩擦因数。由力的分解合成关系可以推出钻头在水平方向受力F_Q为：

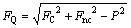           (15)

则刃面上剪切力合力为：

           (16)

根据几何关系，令β=90-θ，则剪切速度v_J和摩擦速度v_M分别为：

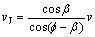             (17)

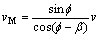             (18)

在稳定的钻掘工作条件下，推力作用下压入岩石的钻头前端面平均温度升高的解析表达式应为：

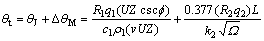 (19)

1.2.2  钻掘过程钻头平均温度

由于钻头的切削面和压入面的尺寸都不是很大，在稳定钻掘的情况下，整个钻头工作面的温度升高可认为是压入面与切削面温度升高之和。

根据文献[5, 15-16]的推导，刀具在扭矩作用下切削岩石时，切削面的平均温度升高可以由下式计算：

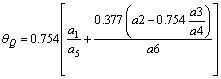     (20)

其中：

。

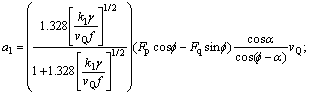
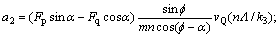
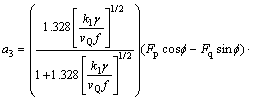
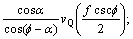
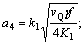
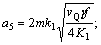
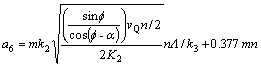式中：γ为剪切区相对滑移系数；f为切削厚度；m为切削宽度；n为切削过程中切屑与刀片摩擦长度；F_p为主切削力；F_q为背向力；v_Q为切削速度；α为切削刃前角。可见，钻头钻掘过程中的平均温度θ_G的解析表达式为：

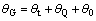           (21)

式中：θ₀为室温。

2  计算分析与试验

2.1  计算分析

相关试验参数如下：室温为10 ℃，灰岩导热系数k₁=2.86 J/(m·s·K)，灰岩导温系数K₁=1.242×10^-6，灰岩切屑导热系数k₂=0.81 J/(m·s·K)，切屑导温系数K₂=6.03×10^-7，灰岩剪切角f=36.69°，前端面压入角θ=60°，刀具切削刃前角α=30°，压入刃宽度U=4 mm，剪切厚度Z=2 mm，切屑接触长度L=1.5 mm，刀片导热系数k₃=79.6 J/(m·s·K)；推力P=325 N，主切削力F_P=620.5 N，背向力F_Q=205.5 N；切削宽度m=5 mm，切削厚度f=13 mm，切屑与刀片摩擦长度n=2.5 mm。切削速度v_Q=190 mm/s。

根据式(22)，代入相关参数进行计算，并忽略二阶小项，当其他条件一定时，推进速度与钻头平均温度之间的关系式为：

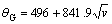          (23)

可以看出：当其他条件一定时，钻头温度的升高与推进速度的平方根成正比，变化趋势如图4所示(v=0时的温度是由切削运动导致发热后的温度)。

2.2  试验

由于岩石钻掘过程中钻头工作条件十分恶劣，想要直接而准确地获取钻头工作面的温度十分困难，国内外许多研究人员在这方面进行了一些尝试，但效果都不太理想。物体各部分温度的差异导致其向外辐射的红外能量特征出现差异，根据这一物理现象，可以利用红外热像仪对物体温度实现非接触式测量，而且随着热成像技术的成熟和完善，热像仪近年来得到广泛应用。本文对红外热像仪在岩石钻掘领域进行应用研究。试验中，使用红外热像仪对钻头退出钻孔时的温度进行测量，为研究钻头工作面的温度变化规律提供间接、半定量参考，并试图为实验方法的进一步优化提供研究基础。

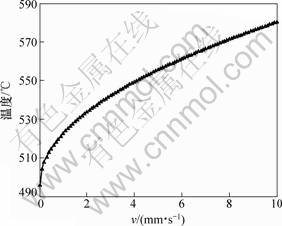
图4  钻头温度随推进速度变化关系

Fig.4  Relationship between temperature variation and Forward speed

具体采用VarioCAM hr-HS 型高灵敏度红外热像仪(热灵敏度0.03 ℃，像素为640×480)对在不同推进速度下钻掘相同深度后的孔口退出温度进行测量，如图5所示。

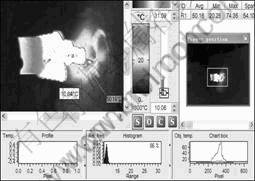
图5  红外线热成像仪测量钻头退出后的温度

Fig.5  Bit temperature after drilling measured by infrared thermal camera

由于钻头在钻进过程中，热功转化集中在尺寸有限的刀刃部分，致使刀刃温度急剧升高。当钻头停止钻进并推出钻孔时，由于工作面刀刃尺寸很小，储热能力有限，钻头温度在短时间内将急速下降，将远远低于其工作时的即时温度。通过对孔口测得的不同钻头退出温度的比较，也可以反映出工作温度的对比关系。

在现场进行了4种不同推进速度下的岩石钻掘试验，钻进相同距离后，退出钻头并在孔口用红外成像仪测量刀刃工作区域平均温度。测量结果与相应推进速度下利用式(23)得到的计算温度见表1。

表1  孔口测量温度与计算工作温度

Table 1  Measured temperature after drilling and calculated working temperature

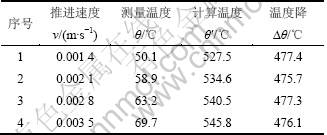
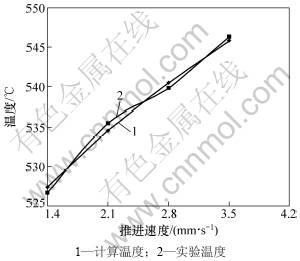
图6  计算温度与实验温度处理值

Fig.6  Calculated temperatures and processed experimental temperatures

4次测量值与计算值之间的平均温度降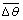为476.6 ℃，则孔口测量温度与平均温度降之和分别为526.6，535.4，540.7和546.3 ℃，与对应速度下的工作温度计算值的误差在10 ℃之内(如图6所示)。从图6可见：由本文推导的解析式计算的平均温度基本反映了实际中钻头工作温度变化规律，也说明利用红外热像仪对岩石钻掘温度进行实验研究的可行性。

3  结论

(1) 通过系统建立钻头-岩石-切屑系统的导热微分方程组，揭示出钻头的工作温度主要受几何条件、材料热物性质、钻掘参数(切削力与切削速度、推力与推进速度等)等一系列复杂因素的影响；该方程组的建立也进一步为数值模拟研究提供了理论依据。

(2) 推导出钻头钻掘岩石过程中工作温度的解析计算模型，而且相关实验体现出的温度变化规律也与计算结果保持了较好的一致性；在其他条件一定情况下，钻头温度的升高与推进速度v的平方根成正比，为工程应用提供了直接有效的参考依据。

(3) 在工程施工中，应根据实际情况将推进速度等参数控制在合理范围内，避免由于工作温度过高造成钻头的早期失效现象。

参考文献：

[1] Uoharo K. Fundamental approach to the thermal crack of cemented cutting tools[J]. Annals of the CIRP, 1981, 30(1): 256-259.

[2] Beste U, Jacobson S. A new view of the deterioration and wear of WC/Co cemented carbide rock drill buttons[J]. Wear, 2008, 264: 1129-1141.

[3] Beste U, Hartzell T, Engqvist H, et al. Surface damage on cemented carbide rock-drill buttons[J]. Wear, 2001, 249: 324-329.

[4] Jorn L B. Wear of hard-metals in rock drilling: a survey of the literature[J]. Powder Metall, 1973, 16: 1-32.

[5] 李晓红, 杨晓峰, 卢义玉, 等. 水射流辅助硬质合金钻头切割岩石过程的刀具温度分析[J]. 煤炭学报, 2010, 35(5): 844-849.
LI Xiao-hong, YANG Xiao-feng, LU Yi-yu, et al. Temperature analysis of cemented carbide drill cutting rock associated with water jet[J]. Journal of China Coal Society, 2010, 35(5): 844-849.

[6] Incropera F P, Dewitt D P. Fundamentals of heat transfer 6th edition[M]. Hoboken: John Wiley & Sons Inc, 2006: 231-257.

[7] Nakayama K. 金属切削加工理论[M]. 北京: 机械工业出版社, 1985: 70-75.
Nakayama K. Theory of metal cutting[M]. Beijing: Mechanical Industry Press, 1985: 70-75.

[8] 张绍和, 鲁凡. 金刚石钻头参数设计规律[J]. 中南大学学报: 自然科学版, 2004, 35(2): 195-200.
ZHANG Shao-he, LU Fan. Designing method about parameters of impregnated diamond bit[J]. Journal of Central South University: Science and Technology, 2004, 35(2): 195-200.

[9] Bever M B, Holt D L, Titchener A L. The stored energy of cold work[M]. Oford, New York: Progress in Materials Science, 1973: 5-177.

[10] Jaeger J C. Moving sources of heat and the temperature at sliding contacts[J]. Proceedings of the Royal Society of New South Wales, 1942, 76: 203-224.

[11] Shaw M C. Metal cutting principles[M]. Oxford: Thetford Press Limited, 1984: 265-297.

[12] Weiner J H. Shear plane temperature distribution in orthogonal machining[J]. Transactions of ASME, 1955, 77: 1331-1341.

[13] Blok H. Theoretical study of temperature rise at surfaces of actual contact under oiliness lubricating conditions[M]. London: Proceedings of General Discussion on Lubrication and Lubricants, Institute of Mechanical Engineers London, 1938: 55-71.

[14] Sikarshie D L, Altiero N T. The formation of chips in the penetration of elastic-brittle materials(Rock)[J]. Trans J of Appl Mechanics, 1973(9): 25-31.

[15] Loewen E G, Shaw M C. On the analysis of cutting tool temperatures[J]. Transactions of the ASME, 1954, 71: 217-231.

[16] Armarego E J A, Karri V, Smith A J R. Fundamental studies of driven and self-propelled rotary tool cutting processes—I. Theoretical investigation[J]. International Journal of Machine Tools and Manufacture, 1994, 34(6): 785-801.

(编辑 陈灿华)

收稿日期：2010-01-01；修回日期：2011-01-26

基金项目：国家自然科学基金委创新研究群体专项基金资助项目(50921063)；重庆市杰出青年基金资助项目(CSTC 2009BA6047)；重庆大学研究生科技创新基金资助项目(201005B1A0010341)

通信作者：杨晓峰(1980-)，男，吉林辽源人， 博士研究生，从事岩石高效破碎基础理论与技术研究；电话：023-65106640；E-mail：act777@126.com