充填管道堵塞风险预测模型

王新民，高瑞文，胡威，冯岩，周登辉

(中南大学 资源与安全工程学院，湖南 长沙，410083)

摘要：建立充填管道堵塞风险预测模型，运用层次分析法和未确知测度理论的基本原理对管道堵塞风险进行综合评判。在预测过程中，综合考虑影响管道堵塞的动态、静态、定量和非定量指标，如料浆流速与临界流速之比、料浆体积分数、管道粗糙度等。其步骤为：首先，利用实测数据建立单指标未确知测度矩阵；然后，通过层次分析法(AHP)计算各指标因素的权重，依照置信度识别准则进行等级判定；最后得到充填管道堵塞风险性预测结果。实例验证结果表明：预测结果与实际结果相符。

关键词：充填管道；未确知测度；预测模型；层次分析法；堵塞

中图分类号：TD235.4          文献标志码：A         文章编号：1672-7207(2013)11-4604-07

Risk prediction model of filling pipeline blockage

WANG Xinmin, GAO Ruiwen, HU Wei, FENG Yan, ZHOU Denghui

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: The AHP (analytical hierarchy process) and the uncertainty measurement theory were used to make a synthetic assessment about the filling pipeline blockage risk based on risk prediction model of filling pipeline blockage. During this process, lots of dynamic and static, fix and non-fix quantified influence factors working on the filling pipeline blocking were taken into account, such as the ratio of slurry flow rate to critical velocity, the volumetric concentration of filling slurry and the absolute roughness of filling pipeline etc. The procedures were as follows. Firstly, uncertainty measurement function was obtained based on the in-situ data. Then, the weights of the influence factors matrix were calculated according to the AHP method and credible degree recognition criteria were established according to the uncertainty measurement theory. And finally, the results of risk prediction were obtained. The prediction results are consistent with the actual ones.

Key words: filling pipeline; uncertainty measurement; prediction mode; AHP; blocking

目前，随着开采深度的逐渐增加，为了更好地控制高地压、高地热，矿山的主体方法都选择充填采矿法^[1]。其中充填系统的合理建造与安全操控是矿山成功实施充填采矿法的关键。在整个充填系统中，管道输送系统是薄弱环节之一，其失效形式主要有爆裂、堵塞和磨损，其中又以堵塞为主，是制约充填技术发展和应用的瓶颈。国内多个矿山的充填系统都发生过严重堵管事故，对生产造成了极大影响，导致巨大的经济损失。所以，对充填管道堵塞风险进行合理预测，可以使矿山提前采取应对措施，避免重大堵管事故的发生。郑晶晶等^[2-3]利用BP神经网络和灰色系统理论对金川矿区充填钻孔的使用寿命及其影响因素进行了分析研究。目前，人们对有关充填管道堵塞方面的研究较少，存在一定的缺陷和不足。充填管道堵塞预测的难点在于许多因素的不确定性和隐蔽性，在这方面，未确知数学理论提供了一种较好途径。王光远^[4]于1990年提出未确知信息及其数学处理理论，它是一种不同于模糊信息、随机信息和灰色信息的新的不确定性信息。在此基础上，刘开第等^[5]建立了未确知数学理论，并将该理论运用到社会科学和自然科学中。在未确知数学的应用研究中，成果最多的是未确知测度评价模型的应用^[6-7]。但是，仅利用未确知测度理论确定复杂的指标体系的权重存在一定不足。层次分析法(AHP)能够将复杂系统问题的各因素通过划分相互联系的各有序层次，使之条理化，根据对一定客观现实的判断，对每一层次相对重要性予以定量表示，利用数学方法确定表达每一层次的全部元素的相对重要次序的权值^[8-10]。为此，将层次分析法^[11]和未确知测度理论^[12]优化结合，构建了充填管道堵塞风险预测模型，并综合考虑充填料浆体积分数(I₁)、管道内径(I₂)、充填料浆的密度(I₃)、充填管道的绝对粗糙度(I₄)、偏斜率(I₅)、充填倍线(I₆)、料浆流速与临界流速之比(I₇)、加权平均粒径(I₈)、充填骨料形状(I₉)及充填料浆的腐蚀性(I₁₀)共10个指标影响。一方面，将定性指标转化为半定量指标进行定量分析，结果更加准确；另一方面，研究对象为充填管道堵塞，弥补了以往研究的不足。

1  充填管道堵塞风险预测模型

1.1  未确知测度理论

设评价对象集X={X₁，X₂，X₃，…，X_n}，评价指标集I={I₁，I₂，…，I_m}。若x_ij表示第i个评价对象X_i关于第j个评价指标I_j的测量值，则有m维向量X_i=(x_i1，x_i2，…，x_im)。设评价等级空间U={C₁，C₂，…，C_p}，第k个评价等级C_k为x_ij的等级值；设第k级比第k+1级危险性大(或安全程度高)，记为C_k＞C_k+1；若C₁＞C₂＞…＞C_p或C₁＜C₂＜…＜C_p，则称{C₁，C₂，…，C_p}是U的一个有序分割类。

若μ_ijk=μ(x_ij∈C_k)表示测量值x_ij属于第k个评价等级C_k的程度，且μ满足：

；

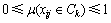i=1, 2, …, n；j=1, 2, …, m；k=1, 2, …, p (1)

；i=1, 2, …, n；j=1, 2, …, m        (2)

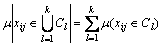；k=1, 2, …, p      (3)

称式(2)为“归一性”，式(3)为“可加性”。满足式(1)，(2)和(3)的μ称为未确知测度，简称测度^[13] 。

1.2  单指标未确知测度矩阵的确定

构造单指标测度函数μ(x_ij∈C_k)(i=1, 2, …, n；j=1, 2, …, m；k=1, 2, …, p)，求出对象X_i的各个指标测度μ_ijk，则称(μ_ijk)_m×p为单指标测度评价矩阵^[14]，即

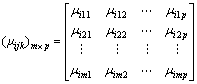        (4)

1.3  层次分析法确定指标权重

1.3.1  比较标度的构造

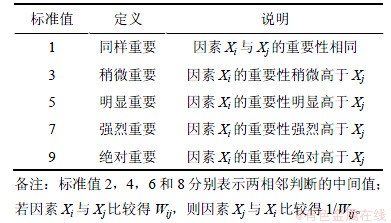
依据两两比较的标度和判断原理，可得出如下标准值为1~9的比较标准^[15]，见表1。

表1  比较标准意义

Table 1  Meanings of comparison standard

1.3.2  构造比较判断矩阵

根据层次模型，每一层都以上一层次为基准，两两比较构造判断矩阵，则有判断矩阵[D]：

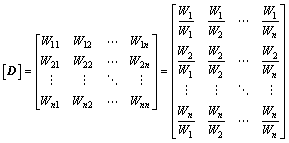         (5)

由上述方法得到的判断矩阵[D]，解特征根问题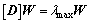：，所得到的W经正规化处理后作为因素的排序权重。不难证明，其最大特征根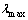存在且唯一。然而，对[D]只能求它们的近似值，得不到精确的特征值和特征向量W ^[16]。本文将采用方根法进行近似计算。

(1) 将判断矩阵[D]的元素按行相乘，得到各行元素乘积M_i：

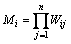              (6)

(2) 计算M_i的n次方根：

               (7)

(3) 向量正规化：

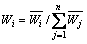             (8)

(4) 判断矩阵的最大特征根计算：

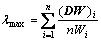            (9)

1.3.3  矩阵的一致性检验

判断矩阵部分结果由于个人主观因素影响，难免存在误差。为使判断结果更加准确，需进行一致性检验。判断矩阵的一致性检验公式为：C_R=C_I/R_I。其中：C_I为检验指标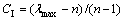，；n为判断矩阵的阶数；R_I为平均随机一致性指标，其取值见表2。

表2  平均随机一致性指标取值

Table 2  Value of average stochastic coincidence indicators

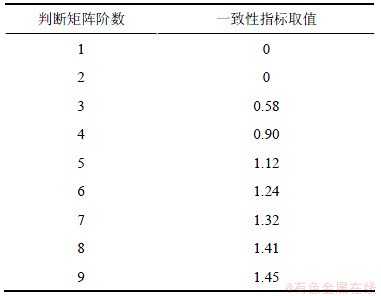
当C_R＜0.1时，判断矩阵[D]符合的一致性检验；否则，需要调整判断矩阵，直至满足要求为止。

1.3.4  权重向量的计算

在判断矩阵满足一致性检验的条件下，求出各层因素的权重向量。

1.4  预测矩阵的确定

若存在μ_ik满足：0≤μ_ik≤1，μ_ik=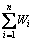·μ_ijk(k=1, 2, …, p)，则称(μ_ik)_n×p为预测矩阵。

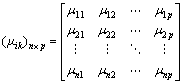          (10)

1.5  预测结果评判

为了得出最终预测结果，引入置信度评价准则^[17]。设λ为置信度(λ≥0.5，通常取λ=0.5或0.6)，若C₁＞C₂＞…＞C_p，且令

     (11)

则认为评价对象的风险等级为。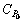

1.6  模型流程

模型流程见图1。

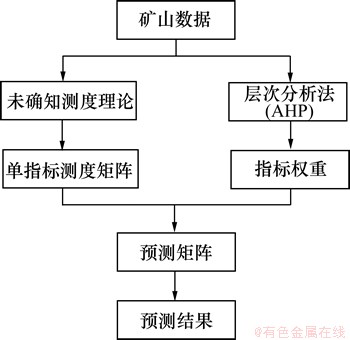
图1  充填管道堵塞风险预测模型流程图

Fig.1  Flow chart of filling pipeline blockage risk prediction model

2  模型验证

2.1  充填管道堵塞风险模型指标体系的建立

参考大量的相关文献，通过赋值的方法将定性指标转变为半定量指标，使其能够参与到模型的构建中，以得到较准确的预测结果。运用分级标准化法将每个指标分为4级，评价等级集为{C₁，C₂，C₃，C₄}，即Ⅰ级、Ⅱ级、Ⅲ级和Ⅳ级，分别表示风险性大、风险性较大、风险性一般、风险性很小。每级都根据专家经验设置一个取值标准，分级标准见表3与表4。

根据表3和表4中各评判指标的赋值标准，构建充填管道堵塞风险各指标的测度函数，据此函数查得各指标的未确知测度。定量指标的单指标测度函数分别如图2~9所示。

表3  充填管道堵塞风险预测模型的定量指标分级标准

Table 3  Classification criterion of quantitative indexes in risk evaluation on blocking of filling pipeline

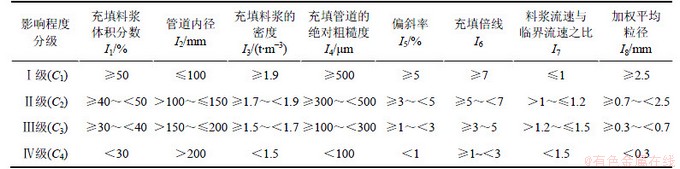
表4  充填管道堵塞风险预测模型的定性指标分级标准

Table 4  Classification criterion of qualitative indexes in risk evaluation on blocking of filling pipeline

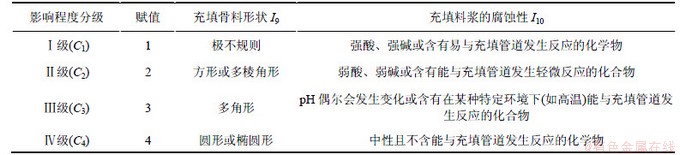
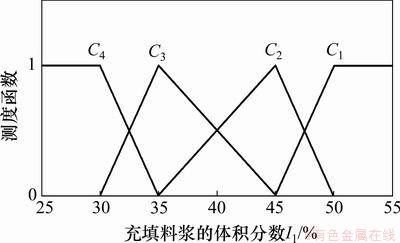
图2  充填料浆体积分数I₁的单指标测度函数

Fig.2  Uncertainty measurement function of volumetric concentration of filling slurry

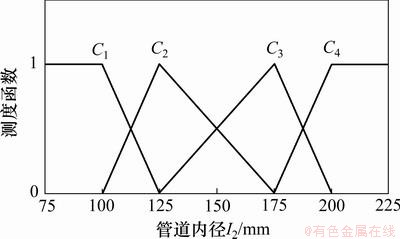
图3  管道内径I₂的单指标测度函数

Fig.3  Uncertainty measurement function of inside diameter of pipelines

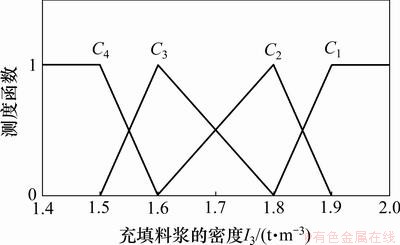
图4  充填料浆密度I₃的单指标测度函数

Fig.4  Uncertainty measurement function of density of filling slurry

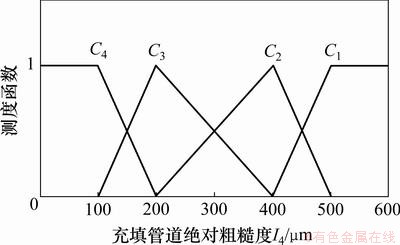
图5  充填管道绝对粗糙度I₄的单指标测度函数

Fig.5  Uncertainty measurement function of absolute roughness of filling pipeline

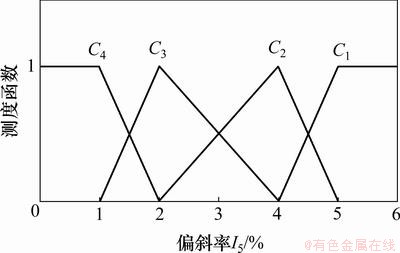
图6  偏斜率I₅的单指标测度函数

Fig.6  Uncertainty measurement function of deviation rate

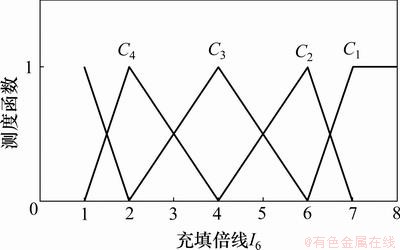
图7  充填倍线I₆的单指标测度函数

Fig.7  Uncertainty measurement function of filling times line

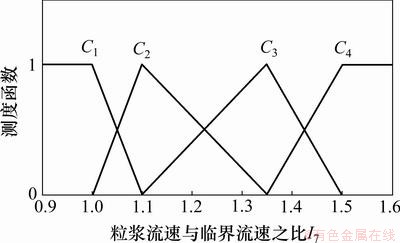
图8  料浆流速与临界流速之比I₇的单指标测度函数

Fig.8  Uncertainty measurement function of ratio of slurry flow rate to critical velocity

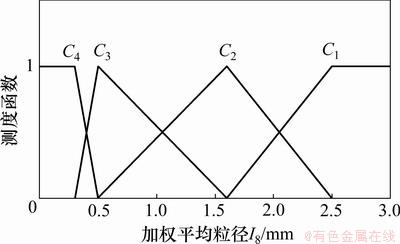
图9  加权平均粒径I₈的单指标测度函数

Fig.9  Uncertainty measurement function ofweighted average grain diameter

2.2  实例验证

2.2.1  确定单指标测度矩阵

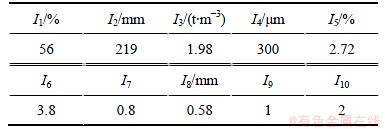
金川龙首矿是国内有丰富充填经验的矿山，结合矿山实际情况，运用上述模型对其充填管道堵塞风险性进行预测。评价对象的充填管道各项指标统计值见表5。将表3中的各项指标统计值代入图2～9对应的单指标未确知测度函数中，得到相应的单指标测度评价矩阵为

      (12)

表5  矿山充填管道各指标统计值

Table 5  Measured data of all indexes of filling pipeline in each mine

2.2.2  指标权重计算

(1) 根据式(5)得到判断矩阵：

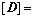
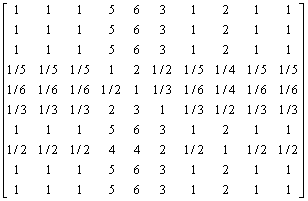         (13)

(2) 根据式(6)~(9)得到金川龙首矿充填管道堵塞风险性评价系统的各指标权重W为

W={0.137 7, 0.137 7, 0.137 7, 0.027 8, 0.020 7, 0.047 8,0.137 7, 0.077 3, 0.137 7, 0.137 7}             (14)

(3) 将以上数据代入一致性检验公式,经计算得C_R=0.004＜0.100，即满足一致性检验，结果可信。

2.2.3  预测结果

由式(10)得预测矩阵μ_ik：

(μ_ik)_1×4=[0.550 9 0.164 5 0.142 10.142 5]    (15)

参见文献[17]，选取置信度λ=0.5，由式(11)可得金川龙首矿的充填管道堵塞风险等级为I级。

3  结论

(1) 通过综合考虑影响充填管道堵塞各个因素，建立了风险预测模型，为研究充填管道堵塞提出了一种科学、系统的方法。

(2) 利用未确知测度和层次分析法相结合的方式，确立了风险预测模型的指标体系。

(3) 预测结果表明，金川龙首矿的堵塞风险为I级，即容易发生堵管，与实际情况相符，证明了该风险预测模型科学合理，意义明确，有一定的推广应用价值

参考文献：

[1] 王新民, 古德生, 张钦礼. 深井矿山充填理论与管道输送技术[M]. 长沙: 中南大学出版社, 2010: 1-6.

WANG Xinmin, GU Desheng, ZHANG Qinli. Theory of backfilling activity and pipeline transportation technology of backfill in deep mines[M]. Changsha: Central South University Press, 2010: 1-6.

[2] 郑晶晶, 张钦礼, 王新民, 等. 基于BP神经网络的充填钻孔使用寿命预测[J]. 湘潭师范大学学报: 自然科学版, 2008, 30(4): 40-44.

ZHENG Jingjing, ZHANG Qinli, WANG Xinmin, et al. Assessment of backfill drilling hole’s life on BP neural network[J]. Journal of Xiangtan Normal University: Natural Science Edition, 2008, 30(4): 40-44.

[3] 郑晶晶, 张钦礼, 王新民, 等. 灰关联法用于充填钻孔使用寿命影响因素分析[J]. 西安科技大学学报, 2009, 29(6): 691-696.

ZHENG Jingjing, ZHANG Qinli, WANG Xinmin, et al. Application of grey related method in analysis of influencing factors on backfill drilling hole’s life[J]. Journal of Xi’an University of Science and Technology, 2009, 29(6): 691-696.

[4] 王光远. 论未确知性信息及其数学处理[J]. 哈尔滨建筑工程学院学报, 1990, 23(4): 52-58.

WANG Guangyuan. Uncertainty information and its mathematical treatment[J]. Journal of Harbin Architecture and Engineering Institute, 1990, 23(4): 52-58.

[5] 刘开第, 吴和琴, 庞彦军, 等. 不确定性信息数学处理及应用[M]. 北京: 科学出版社, 1999: 55-59.

LIU Kaidi, WU Heqin, PANG Yanjun, et al. Mathematics treatment and application of uncertainty information[M]. Beijing: Science Press, 1999: 55-59.

[6] 吴义锋, 薛联青, 吕锡武. 基于未确知数学理论的水质风险评价模式[J]. 环境科学学报, 2006, 26(6): 1047-1052.

WU Yifeng, XUE Lianqing, L Xiwu. Assessment model of water quality risk based on unascertained mathematics theory[J]. Acta Scientiae Circumstantiae, 2006, 26(6): 1047-1052.

[7] 阳富强, 吴超. 基于未确知测度理论的硫化矿石爆堆自燃危险性评价[J]. 中南大学学报: 自然科学版, 2010, 41(6): 2373-2380.

YANG Fuqiang, WU Chao. Risk assessment on spontaneous combustion of sulfide ore dump in stope based on uncertainty measurement theory[J]. Journal of Central South University: Science and Technology, 2010, 41(6): 2373-2380.

[8] 罗一忠, 吴爱祥, 胡国斌, 等. 采场人-机-环境系统可靠性模糊综合评价[J]. 中南大学学报: 自然科学版, 2006, 37(4): 804-809.

LU Yizhong, WU Aixiang, HU Guobin, et al. Reliability fuzzy comprehensive evaluation of man-machine-environment system in stope[J]. Journal of Central South University: Science and Technology, 2006, 37(4): 804-809.

[9] 许传华, 任青文. 地下工程围岩稳定性的模糊综合评判法[J]. 岩石力学与工程学报, 2004, 23(11): 1852-1855.

XU Chuanhua, REN Qingwen. Fuzzy synthetic evaluation on stability of surrounding rock-mass of underground engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(11): 1852-1855.

[10] 王新民, 赵彬, 张钦礼. 基于层次分析和模糊数学的采矿方法选择[J]. 中南大学学报: 自然科学版, 2008, 39(5): 875-880.

WANG Xinrain, ZHAO Bin, ZHANG Qinli. Mining method choice based on AHP and fuzzy mathematics[J]. Journal of Central South University: Natural Science, 2008, 39(5): 875-880.

[11] 李俊芳, 吴小萍. 基于AHP-FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J]. 武汉理工大学学报, 2007, 4(2): 205-208.

LI Junfang, WU Xiaoping. Synthetic evaluation for urban rail transit line network planning scheme based on AHP-FUZZY method[J]. Wuhan: Wuhan Engineering University, 2007, 4(2): 205-208.

[12] 李树刚, 马超, 王国旗. 基于未确知测度理论的矿井通风安全评价[J]. 北京科技大学学报, 2006, 28(2): 101-103.

LI Shugang, MA Chao, WANG Guoqi. Colliery ventilation safety evaluation on the basis of uncertainty measurement[J]. Journal of University of Science and Technology Beijing, 2006, 28(2): 101-103.

[13] 宫凤强, 李夕兵, 董陇军, 等. 基于未确知测度理论的采空区危险性评价研究[J]. 岩石力学与工程学报, 2008, 27(2): 323-330.

GONG Fengqiang, LI Xibing, DONG Longjun, et al. Underground goaf risk evaluation based on uncertainty measurement theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 323-330.

[14] 李如忠, 洪天求, 熊鸿斌, 等. 基于未确知数学理论的沉积物重金属污染评价模式[J]. 农业环境科学学报, 2007, 26(6): 2167-2172.

LI Ruzhong, HONG Tianqiu, XIONG Hongbin, et al. Assessment model for heavy metal pollution in stream sediments based on uncertainty mathematics theory[J]. Journal of Agro-Environment Science, 2007, 26(6): 2167-2172.

[15] 黄贯虹, 方刚. 系统工程方法与应用[M]. 广州: 暨南大学出版, 2005: 25-30.

HUANG Guanhong, FANG Gang. System engineering method and application[M]. Guangzhou: Jinan University Press, 2005: 25-30.

[16] 许宝田, 阎长虹, 许宏发, 等. 基于模糊理论的软岩弹性模型识别及参数反分析[J]. 岩石力学与工程学报, 2006, 25(11): 2280-2286.

XU Baotian, YAN Changhong, XU Hongfa, et al. Viscidity-elastic model identification and back analysis of parameters of soft rock on fuzzy theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2280-2286.

[17] 刘开第, 庞彦军, 孙光勇, 等. 城市环境质量的未确知测度评价[J]. 系统工程理论与实践, 1999, 19(12): 52-58.

LIU Kaidi, PANG Yanjun, SUN Guangyong, et al. The unascertained measurement evaluation on a city’s environmental quality[J]. Systems Engineering: Theory and Practice, 1999, 19(12): 52-58.

(编辑  陈灿华)

收稿日期：2012-11-19；修回日期：2013-01-25

基金项目：国家“十一五”国家科技支撑计划项目(2008BAB32B03)

通信作者：王新民(1957-)，男，安徽安庆人，教授，从事采矿与充填技术研究与教学工作；电话：0731-88879612；E-mail: wxm1958@126.com