基础条件对SSDI体系动力特性的影响

夏栋舟¹，何益斌²

(1. 长沙理工大学 土木与建筑学院，湖南 长沙，410076；

2. 湖南大学 土木工程学院，湖南 长沙，410082)

摘要：基于影响土-结构动力相互作用(SSDI)体系抗震性能和动力特性的因素除地基土特性与上部结构特性外，基础作为联系上部结构和土体的桥梁，其构造形式以及埋置深度对SSDI体系动力性能的影响不可忽视。通过采用有限元方法，对某工程高层建筑算例进行计算分析；利用ANSYS程序中重新启动法、APDL参数设计语言编制程序实现对地基土的非线性模拟，并通过土体边界、土体与结构间非线性接触的研究，对整个SSDI体系在实测地震波作用下的动力反应进行计算分析，研究桩筏基础、桩箱基础2种不同基础形式以及不同基础埋深条件对上部结构动力反应效应的影响。研究结果表明：桩箱基础条件时上部结构动力反应较小，基础埋深越大，上部结构动力反应越小。研究成果为工程抗震设计考虑基础条件对土-结构动力相互作用效应的影响提供了理论依据，对完善抗震设计规范具有参考价值。

关键词：基础形式；基础埋深；土-结构动力相互作用；非线性；有限元；动力特性

中图分类号：TU435         文献标志码：A         文章编号：1672-7207(2012)07-2775-07

Influence of dynamic behaviors for SSDI system based on different foundation conditions

XIA Dong-zhou¹, HE Yi-bin²

(1. School of Civil Engineering, Changsha University of Science and Technology, Changsha 410076, China;

2. College of Civil Engineering, Hunan University, Changsha 410082, China)

Abstract: Based on the fact that the influence factors of dynamic characteristics and aseismic capability for soil- structure-dynamic-interaction (SSDI) system include the soil characteristics and structural characteristics, and the foundation acted as a bridge associating structure with soil, its forms, as well as embedded depth cannot be ignored. Using the ANSYS program of finite element method, non-linear simulation of the soil and dynamic responses of SSDI system was achieved with restart method, APDL parameter design language program and simulating soil boundaries, soil and structure nonlinear contact under the action of seismic waves was measured. Many issues were studied such as the changes of the structural dynamic characteristics under pile-raft foundation and pile-box foundation conditions, as well as the dynamic response effects of upper structure in different foundation embedments. The results show that dynamic response of upper structure is small in pile-box foundation condition, and the foundation embedment is bigger, the upper structure dynamic response is smaller. Theoretical evidence is provided for the seismic design by considering foundation conditions of soil-structure-dynamic-interaction system, and the research results have reference value for the code of seismic design.

Key words: foundation forms; foundation embedment; soil-structure-dynamic-interaction; nonlinearity; finite element; dynamic characteristics

土-结构动力相互作用(Soil-structure-dynamic- interaction，简称SSDI)问题是一个涉及土动力学、结构动力学、非线性振动理论、地震工程学、岩土及结构抗震工程学、计算力学及计算机技术等众多学科的交叉性研究课题^[1-8]。自20世纪80年代中期至今，相互作用问题一直是土木工程领域研究的重点与难点，Javier等^[9-10]对地基基础与上部结构动力相互作用体系阻尼性能与抗震性能进行了研究，指出在工程实际中地基土、基础以及上部结构阻尼特性的变化均会影响土-结构动力相互作用体系的动力性能。同时，国内外很多研究者也通过进行大规模的模型试验和现场振动试验^[11-13]研究了地基土特性、上部结构特性以及基础特性等因素对SSDI体系相互作用效应的影响。其中，基础作为联系上部结构和土体二者间的桥梁，其构造形式的变化以及埋置深度的改变对整个SSDI体系动力性能的影响不可忽视。虽然已有研究者对埋置基础的相似模型进行了研究^[14]，但关于基础具体特性指标对SSDI体系动力特性的影响的研究很少。为此，本文作者采用有限元方法，并通过ANSYS程序中重新启动法^[15-16]，利用APDL参数^[16]设计语言编制程序实现土介质的非线性模拟；通过对土体与结构接触界面的状态非线性以及土体边界条件的模拟，对SSDI体系网格进行合理划分，由此对某工程高层建筑算例进行计算分析，对比研究桩筏基础、桩箱基础等条件下结构动力特性指标的变化规律以及不同基础埋深条件下上部结构各层的动力反应效应，以便为工程抗震设计和实践中考虑土-结构动力相互作用效应提供理论依据。

1  工程实例基本概况

某工程高层建筑上部结构为钢筋混凝土现浇框架，共12层，其结构计算参数如表1所示，结构平面形式如图1所示。建筑使用现浇混凝土楼盖，各层现浇楼板厚为120 mm，各层柱梁宽×梁高均为600 mm×600 mm，走道横梁梁宽×梁高为250 mm×400 mm，其他横梁及边梁梁宽×梁高为250 mm×600 mm，纵梁梁宽×梁高为250 mm×500 mm，结构及基础混凝土强度等级均采用C30。

基础形式采用2种工况：第1种为桩筏式，其平面布置如图2所示，筏板厚800 mm，桩截面长×宽为600 mm×600 mm，桩长为19 m；第2种工况保持土体参数和上部结构参数不变，基础采用桩箱式，其箱基顶板厚为400 mm，底板厚为600 mm，箱基外墙厚为500 mm，内墙厚为300 mm。场地土均为分层地基土，其地基土体参数和分层情况如表2所示。

表1  结构计算参数

Table 1  Calculating parameters for structure

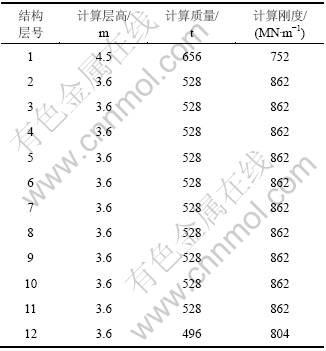
图1  柱网平面布置示意图

Fig.1  Layout plan of column grid

图2  基础平面布置示意图

Fig.2  Layout plan of foundation

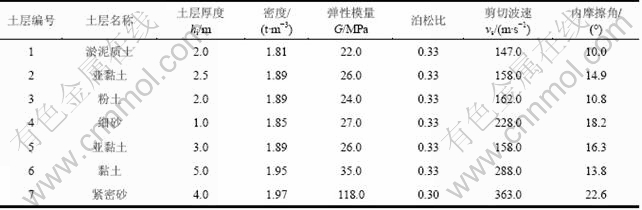
表2  分层地基土力学参数

Table 2  Mechanical parameters of layered soil

2  有限元建模方法及地震波的选取

为了更好地研究本工程实例在地震作用下土-结构动力相互作用体系的动力特性及地震反应规律，通过对实例进行ANSYS有限元建模，解决土体的非线性动力本构模型的模拟、土体边界问题、土体与结构间的动力非线性接触问题以及阻尼模型的选取问题，同时，选定实测地震波作为地震输入条件。

2.1  土体动力本构模型

为了更好地模拟土体非线性，采用等效线性化方法，根据文献[16]中方法，土体模拟选用Davidenkov模型；同时，由于实例中基岩上卧土的土层厚度为19.5 m，因此，其动剪切模量G_d及动阻尼比D的选取按照文献[17]中介绍的常规类土(10＜土体埋深≤20 m)的实验土样进行取值。用ANSYS有限元程序重启动法模拟土的本构模型，具体流程如下：首先进行初始分析，假定土体的动剪切模量为G_d1，阻尼比为D₁，其值均为常数，通过ANSYS程序计算各土层平均应变，然后对计算所得的结果进行处理，利用公式计算相应的动剪切模量G_d2以及阻尼比D₂，再在前一步分析的基础上，采用修改后的动剪切模量和阻尼比。这里需要修改的动剪切模量与阻尼比数据可以采用参数的方式进行定义，根据计算得到的结果修改这些参数，然后作为一个外部文件保存在磁盘上。在重新启动时，将这些数据文件以参数的方式读入，然后，用这些参数修改数据库中的相关数据进行求解，这就需要用APDL参数设计语言来编制程序，实现对土体材料的非线性模拟。

2.2  接触界面状态非线性及阻尼模型参数的选取

利用ANSYS程序中的接触单元对接触截面的状态进行非线性分析。将交界面处的土表面作为接触面，结构表面刚度比土体的大，将其作为目标面，在接触面上形成接触单元，在目标面上形成目标单元，然后，通过相同的实常数将对应的接触单元和目标单元定义为1个接触对，并假定接触面上存在库仑摩擦，通过选择合理的参数，可实现土与结构界面上的黏结、滑移、脱离、再闭合的状态模拟，如图3所示。

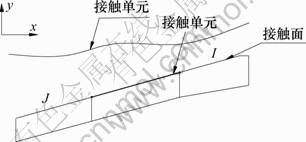
图3  ANSYS接触单元示意图

Fig.3  Contact element in ANSYS

ANSYS程序中可以定义5种形式的阻尼：Alphad和Beta阻尼(即Rayleigh阻尼)、与材料相关的阻尼、恒定阻尼比、振型阻尼和单元阻尼。

Alphad阻尼在模型中引入任意大质量时会出现不理想的结果。Beta阻尼和材料阻尼在非线性分析时会导致与实际不相符合的情况，这2种阻尼要与刚度矩阵相乘，而刚度矩阵在非线性分析中是不断变化的。随着非线性的发展，刚度下降导致Beta阻尼或材料阻尼减小，但结构的实际阻尼会增大。因此，与材料相关的阻尼被当作材料性质来定义，可以解决不同材料阻尼不同的问题。振型阻尼可用于对不同的振动模态定义不同的阻尼比，同时，单元阻尼也可用于有黏性阻尼特征的单元类型。因此，在本算例分析中应该选取一种模型来定义多种形式的阻尼，程序按定义的阻尼进行耦合形成阻尼矩阵[C]。阻尼矩阵[C]的通用形式为：

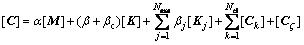   (1)

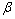其中：为质量矩阵常系数；[M]为质量矩阵；为刚度矩阵常系数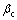；为刚度矩阵变系数；[K]为刚度矩阵；N_mat为按材料阻尼形式输入的材料数目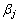；为第j种材料的刚度矩阵常系数；[K_j]为第j种材料的刚度矩阵；N_el为定义单元阻尼的单元数目；[C_k]为第k个单元的阻尼矩阵；为基于频率的阻尼矩阵。由此得到的阻尼模型需要对其中的结构和土体的模型参数进行选取与修正，具体按照文献[18]进行选用。

2.3  边界条件的处理及计算模型的网格划分

对土-结构动力相互作用问题进行有限元分析时，需要对半无限介质的土体进行模拟，而通常有限元软件只能选取有限的土体范围进行计算。为了尽量缩小所选取的土体范围，并考虑由结构产生的散射波从有限计算区域穿过时不发生反射效应，需要在截取的土体边界上建立人工边界来模拟辐射阻尼效应。因此，在计算时采用黏弹性边界，即在边界上设置由线性弹簧和黏性阻尼器的简单分布力学模型来吸收射向人工边界的波动能量。根据文献[19]，由于本算例中结构横向及纵向尺寸相当，因此，在计算时土体横向宽度取桩基础宽度的10倍，竖向取桩基础深度的4倍，侧面和底部均采用ANSYS中Combin14来模拟黏弹性边界，其基本模型的边界示意图如图4所示。

在利用ANSYS对土-结构动力相互作用体系进行网格划分时，土体、桩采用三维实体单元，上部结构采用框架形式，梁和柱采用三维梁单元，楼板和筏板采用三维壳单元。

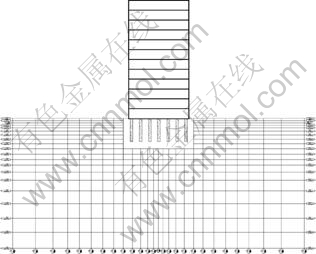
图4  土-结构模型边界条件示意图

Fig.4  Boundary condition of soil-structure model

2.4  地震波的选用

本算例选用EI-Centro地震波，其地震波加速度峰值为3.42 m/s²，波形图如图5所示，于土体底部输入单向地震波。

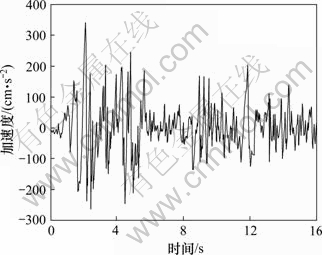
图5  EI Centro(E-W)地震波时程曲线图

Fig.5  Time travel curve of seismic wave EI Centro (E-W)

3  基础形式对SSDI体系动力反应的影响

通过ANSYS有限元程序的建模，对桩筏基础和桩箱基础2种不同形式下体系的动力特性进行计算分析，体系自振频率的对比如表3所示；结构不同高度处加速度峰值、位移峰值、最大层间剪力和最大倾覆力矩的对比示意图如图6~9所示。

表3 不同基础形式时SSDI体系自振频率对比

Table 3  Natural vibration frequencies of SSDI system based on different foundation forms               Hz

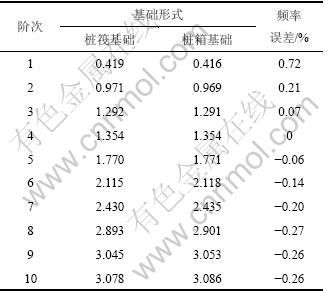
从表3可见：在桩筏基础条件下，体系的前3阶频率均比桩箱基础的大；而在高阶振型中，桩筏基础条件下体系的频率则比桩箱基础时的小。其原因是：桩箱基础比桩筏基础与土壤的接触面积大，在振动初期与土的协同工作性能较差，从而导致其振动频率比桩筏基础的小，随着振型阶次的增加，振动频率相应增大，此时，与土壤接触面积大的桩箱基础与土体动力相互作用效应增强，导致振动频率的增长幅度相应比桩筏基础的大，从而从第3阶振型后桩箱基础条件下体系的频率要比桩筏基础条件下的体系频率大。

从图6~9可知：桩筏基础时结构中，下部的加速度均大于桩箱基础时的相应值；而在结构顶层，桩筏基础时结构的加速度则小于桩箱基础时的相应值；桩筏基础时结构的位移在下面几层均大于桩箱基础时的相应值，而在结构上面几层的规律相反；结构的最大层间剪力和最大倾覆力矩在桩筏基础条件时均大于桩箱基础条件时的相应值。造成上述现象的原因可能是桩箱基础与土体接触面要比桩筏基础的大，从而与土体共同作用所产生的阻尼耗能会降低上部结构的地震反应。

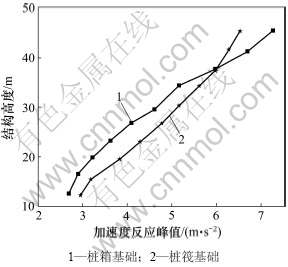
图6  不同基础形式时结构加速度峰值对比

Fig.6  Peak-acceleration of structure based on different foundation forms

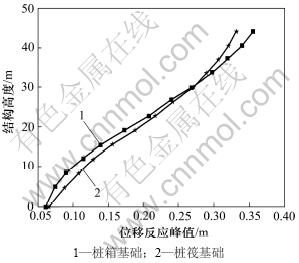
图7  不同基础形式时结构位移峰值对比

Fig.7  Peak-displacement of structure based on different foundation forms

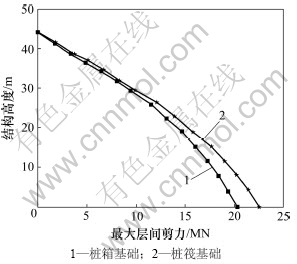
图8  不同基础形式时结构最大层间剪力对比

Fig.8  Maximum inter-story shearing force of structure based on different foundation forms

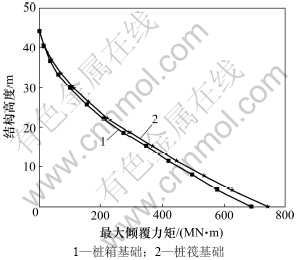
图9  不同基础形式时结构最大倾覆力矩对比

Fig.9  Maximum overturning moment of structure based on different foundation forms

4  基础埋深对SSDI体系动力反应的影响

体系阻尼性能不仅与上部结构、地基土、基础类型等因素有关，同时还与基础埋深有关，因此，由基础埋深导致的阻尼耗能机理的变化势必会影响整个 土-结构动力相互作用体系的动力特性。为此，将算例中桩箱基础条件下的SSDI体系增加一层地下室，其埋置深度分别为3.0，4.5和6.0 m进行变化，上部结构和土体参数均不发生改变，通过ANSYS有限元法对土-结构动力相互作用体系动力反应进行分析对比，得出一般规律，其自振频率对比如表4所示，动力反应计算结果如图10~11所示。

表4  不同基础埋深时SSDI体系的自振频率比较

Table 4  Natural vibration frequencies of SSDI system based on different foundation embedments         Hz

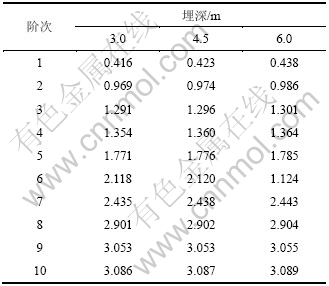
从表4可见：随着基础埋深的增加，其自振频率相应呈增大趋势。这同日本原子能工学试验中心公布的试验结果规律一致。

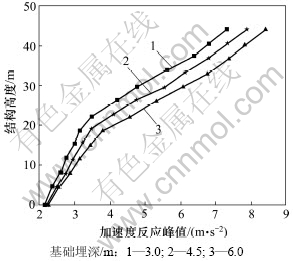
图10  不同基础埋深时结构加速度峰值对比

Fig.10  Peak-acceleration of structure in different foundation embedment

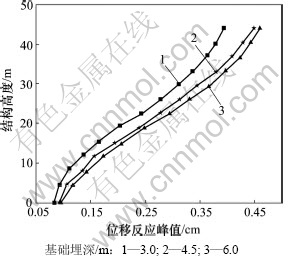
图11  不同基础埋深时结构位移反应峰值对比

Fig.11  Peak-displacement of structure in different foundation embedments

从图10~11可见：随着基础埋深的增加，上部结构的动力反应相应较小，同时，体系上部结构的位移反应峰值相应变小。产生这种动力反应的原因主要是随着基础埋深的增加，桩-土相互作用增强，导致SSDI体系的耦合阻尼比相应增大，从而整个体系的耗能减震性能也会增强，导致上部结构动力反应效应减小。可见：研究基础埋置深度对结构动力反应以及抗震性能的影响有重要作用。本文针对基础埋深问题进行的数值模拟结果为实验验证与规范的制定提供了理论依据。

5  结论

(1) 在桩筏基础时，SSDI体系的前3阶频率均比桩箱基础的大；而在高阶振型中，桩筏基础条件下体系的频率则比桩箱基础的小。

(2) 桩筏基础时结构中下部的加速度均大于桩箱基础时的相应值，而在结构顶层，桩筏基础时结构的加速度则小于桩箱基础时的相应值；桩筏基础时结构的位移在下面几层均大于桩箱基础时的相应值，而在结构上面几层的规律相反；结构的最大层间剪力和最大倾覆力矩在桩筏基础条件时均大于桩箱基础条件时的相应值。可见：由于桩箱基础与土体接触面比桩筏基础的大，从而与土体共同作用所产生的阻尼耗能会降低上部结构的地震反应。

(3) 随着基础埋深的增加，SSDI体系自振频率相应呈增大趋势。

(4) 随着基础埋深的增加，上部结构的动力反应相应减小；随着基础埋深的增加，SSDI体系的阻尼比有所增大，从而整个体系的耗能减震性能也会随之增强，这导致上部结构动力反应减小。

(5) 基础形式与基础埋置深度的变化会导致整个SSDI体系阻尼性能发生变化，从而影响其动力特性的改变。因此，在进行结构的工程抗震设计时，必须考虑基础条件的变化对上部结构地震作用的影响。现有抗震设计规范对上下部共同作用的规定比较笼统，因此，本文研究成果可以为规范考虑土-结构动力相互作用效应提供相应理论依据。

参考文献：

[1] 王松涛, 曹资. 现代抗震设计方法[M]. 北京: 中国建筑工业出版社, 1997: 1-5.
WANG Song-tao, CAO Zi. Modern seismic design method[M]. Beijing: China Architecture & Building Press, 1997: 1-5.

[2] 曹志远. 结构与介质相互作用理论及其应用[M]. 南京: 河海大学出版社, 1993: 1-21.
CAO Zhi-yuan. Theory and application for structure and medium interaction[M]. Nanjing: Hohai University Press, 1993: 1-21.

[3] Novak M, Hifanwy L E L. Effect of soil-structure interaction on damping of structures[J]. Earth Eng And Struct Dyn, 1983, 11: 595-621.

[4] Stewart J P, Seed R B, Fenves G L. Seismic soil-structure interaction in building (Ⅰ): Analytical methods[J]. Geotechnical and Geoenvironmental Engineering, 1999, 9: 38-48.

[5] Enrique L J. A simple model for structural control including soil-structure interaction effects[J]. Earthquake Engineering and Structural Dynamics, 1998, 27(3): 225-242.

[6] Allison S H. Effective optimal structural control of Soil-Structure Interaction systems[J]. Earthquake Engineering and Structural Dynamics, 1997, 26(5): 549-570.

[7] Oliveto G, Santini A. Time domain response of a one- dimensional soil-structure interacting model via complex analysis[J]. Engineering Structures, 1996, 18: 425-436.

[8] Humar J L, Bagchi A, Xia H. Frequency domain analysis of soil-structure interaction[J]. Computer and Structure, 1998, 66(23): 337-351.

[9] Javier A, Martha S. Effective periods and damping of building- foundation systems including seismic wave effects[J]. Engineering Structures, 2002, 24: 553-562.

[10] Raychowdhury P. Seismic response of low-rise steel moment- resisting frame (SMRF) buildings incorporating nonlinear soil- structure interaction[J]. Engineering Structures, 2011, 33(3): 958-967.

[11] Futaki M, Tseng W S. Experiments about seismic performance of reinforced earth retaining wall[C]//Proc 11 WCEE. 1996: 1083.

[12] Hadjian A H, Tseng W S, Chang C Y, et al. 罗东 (台湾)土-结构相互作用大比例模型试验的启示(Ｉ)[J]. 谢君斐, 译. 世界地震工程, 1993(3): 41-52.
Hadjian A H, Tseng W S, Chang C Y, et al. Luodong (Taiwan) soil structure interaction of large scale model test of the enlightenment (Ⅰ)[J]. XIE Jun-fei, transl. World Earthquake Engineering, 1993(3): 41-52.

[13] Hadjian A H, Tseng W S. 罗东 (台湾)土-结构相互作用大比例模型试验的启示(Ⅱ)[J]. 谢君斐, 译. 世界地震工程, 1993(4): 49-59.
Hadjian A H, Tseng W S. Luodong (Taiwan) soil structure interaction of large scale model test of the enlightenment (Ⅱ)[J]. XIE Jun-fei, transl. World Earthquake Engineering, 1993(4): 49-59.

[14] Wolf J P. Approximate dynamic model of embedded foundation in time domain[J]. Earthquake Engineering and Structure Dynamics, 1986, 14: 683-703.

[15] 何益斌, 夏栋舟, 黄欣荣, 等. 土-桩-框架结构动力相互作用非线性有限元模拟[J]. 沈阳建筑大学学报: 自然科学版, 2008, 24(3): 428-432.
HE Yi-bin, XIA Dong-zhou, HUANG Xin-rong, et al. Nonlinear finite element analysis of soil-pile-frame structure-interaction system[J]. Journal of Shenyang Jianzhu University: Natural Science, 2008, 24(3): 428-432.

[16] 何益斌, 夏栋舟, 闫岩, 等. 基于场地土非线性性质的SSDI体系动力特性研究[J]. 岩土工程学报, 2009, 31(4): 521-527.
HE Yi-bin, XIA Dong-zhou, YAN Yan, et al. Dynamic behaviors of SSDI system based on nonlinearity of soil in site[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 521-527.

[17] 孙静. 岩土动剪切模量阻尼试验及应用研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2004: 88-126.
SUN Jing. Laboratory experimental and application study on dynamic shear modulus ratio and damping ratio of soils[D]. Harbin: China Seismological Bureau. Institute of Engineering Mechanics, 2004: 88-126.

[18] 夏栋舟. 土-结构动力相互作用(SSDI)体系阻尼性能及其地震反应分析与研究[D]. 长沙: 湖南大学土木工程学院, 2009: 23-118.
XIA Dong-zhou. Research on damping properties and seismic response of soil-structure-dynamic-interaction (SSDI) system[D]. Changsha: Hunan University. College of Civil Engineering, 2009: 23-118.

[19] 李培振. 结构-地基动力相互作用体系的振动台试验及计算模拟分析[D]. 上海: 同济大学结构工程与防灾研究所, 2002: 91-125.
LI Pei-zhen. The computational analysis and shaking table test for soil-structure interaction system[D]. Shanghai: Tongji University. Research Institute of Structural Engineering and Disaster Reduction. 2002: 91-125.

(编辑 陈灿华)

收稿日期：2011-09-15；修回日期：2011-11-12

基金项目：国家自然科学基金资助项目(50778070；51108044)

通信作者：夏栋舟(1979-)，男，湖南益阳人，博士，讲师，从事土-结构动力相互作用与抗震防灾减灾等研究；电话：18674815855；E-mail: xiadongzhou7941@163.com