Superplasticity and superplastic instability of AZ31B magnesium alloy sheet
WANG Ling-yun(汪凌云)1, SONG Mei-juan(宋美娟)1, 2, LIU Rao-chuan(刘饶川)2
1.College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China;
2.Department of Mechanical Engineering,
Chongqing University of Science and Technology, Chongqing 400050, China
Received 8 August 2005; accepted 12 November 2005
Abstract: Superplastic deformation mechanism of AZ31B magnesium alloy sheet was investigated. Maximum elongation of 216% and strain rate sensitivity of 0.36 were obtained at 723 K and a strain rate of 1×10-3s-1. It is found that dynamic recrystallization occurs at the early deformation stage, and that grain boundary sliding is the dominant deformation mode of superplastic AZ31B sheet, whose fracture is due to the growth and interlinkage of cavities nucleated at grain boundary. A cavity growth model was established, and damage characteristic parameters as well as the critical value of damage variable were identified so as to provide a theoretical ground on which the plastic forming technology of magnesium alloy sheet can be optimized.
Key words: AZ31B magnesium alloy; superplasticity; superplastic instability; strain sensitivity; cavity evolution; damage
1 Introduction
Due to its light mass, high specific strength, good damping characteristics, strong thermo-conductivity and electromagnetic shielding, magnesium alloys have been regarded as “the green material” with the greatest application potential in the 21st century”[1-3], and have found its wide usage in aerospace, electronics fields and particularly in automobile industry. However, magnesium alloys exhibit poor ductility at room temperature because of limited availability of slip systems in hexagonal crystal structure, so their recent fabrications have been mainly performed by die casting. Magnesium alloys surely will find a wider application when its forming technology is improved. Superplastic forming has been proven to play an effective role in complex part fabrications, therefore superplasticity of magnesium alloys under varied deformation conditions has drawn extensive attention of scholars at home and aboard[4-11].
Superplastic deformation is associated with the nucleation, growth and subsequent interlinkage of cavities that leads to rupture. Hence, it is necessary to have a quantitative analysis of cavity evolution law under superplastic deformation so that the prediction on superplastic instability of AZ31B sheet and optimization of the plastic forming technology can be achieved. Up to now, there are few literatures concerning internal damage of superplastic magnesium alloys. BAE and GHOSH[12] established a cavity growth model of superplastic Al-Mg alloys at elevated temperature after analyzing the physical mechanism of cavity formation and early cavity growth. chow and CHAN[13] studied the cavity evolution of coarse-grained Al5052 in superplastic deformation. LIU and WANG[1] proposed the damage evolvement equation of superplastic LY12CZ aluminum alloy on the basis of continuous damage model established by Lemitre within the infrastructure of irreversible thermodynamics. There is an ever-increasing interest about this respect from scholars in fields of materials and mechanics[14-16].
Superplasticity and deformation mechanism of AZ31B magnesium alloy sheet were experimentally investigated in this study. A cavity growth model was established, and damage characteristic parameters as well as the critical value of damage variable were identified so as to provide a theoretical ground on which the plastic forming technology of AZ31B magnesium alloy sheet can be optimized.
2 Experimental
2.1 Material and specimen
The material used in this study was an industrial AZ31B magnesium alloy containing Al 2.92%, Zn 1.01% and Mn 0.34% by mass. The alloy ingot machined to 40 mm thickness was homogenized at 733 K for 6 h and subsequently hot rolled at 723 K by each pass reduction of 15%-20%. When the temperature dropped to below 573 K, it was heated again at 703 K for 1 h.
Tensile specimens with gauge dimensions of 3.5 mm×6 mm×15 mm and 1.5 mm×6 mm×15 mm were machined from the sheet along the rolling direction. Microstructure observation and measurement of linear intercept grain sizes were carried out on an optical microscope. Fig.1 shows the initial microstructure of hot rolled AZ31B sheet, whose mean grain size is about 17.5 μm.
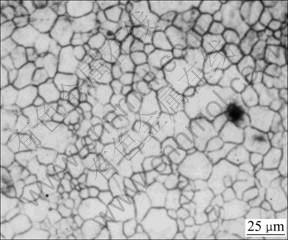
Fig.1 Initial microstructure of hot rolled AZ31B sheet
2.2 Experimental procedure
The tests were performed in the air and on a HT-9102 testing machine whose furnace has 3 heating zones independently controlled to maintain temperature within ±1 K of the test temperature. The specimens were not coated with oxidation resistance layer. The testing temperature range was 673-763 K, and strain rate range was 1×10-4-1×10-3 s-1. Strain rate sensitivity, flow stress and elongation were experimentally measured before the optimized superplastic forming temperature and strain rate for AZ31B sheet can be determined.
Cavity observation was conducted on longitudinal section of specimen (1.5 mm×6 mm×15 mm) deformed at 673 and 723 K with corresponding strain rates of 3.3×10-4 and 1×10-3 s-1. Cavity volume fraction and cavity radius were quantitatively analyzed with self-developed cavity detection software.
3 Results and discussion
3.1 Superplasticity of AZ31B sheet
Industrial AZ31B sheet exhibits high ductility at 673-763 K and strain rate of 1×10-4-1×10-3 s-1. As shown in Fig.2, maximum elongation of 216% and strain rate sensitivity of 0.36 are obtained at 723 K and a strain rate of 1×10-3 s-1. Fig.2 shows that when the true strain reaches the maximum at about 0.3, the flow stress drops slowly to 2.16 when the specimen fractures.
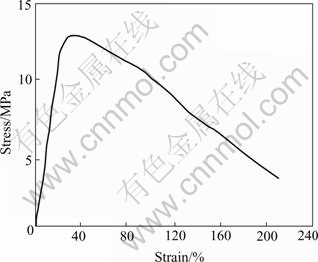
Fig.2 True stress—strain curve of AZ31B specimen deformed at 723 K and a strain rate of 1×10－3 s－1
In order to investigate the flow behavior of hot rolled AZ31B sheet, the peak flow stress as function of strain rate is shown in Fig.3. It indicates that the increase in peak flow stress is associated with rise in strain rate and drop in temperature. Fig.4 shows the variation in elongation to failure as a function of strain rate at different temperatures.
Fig.3 Variation of flow stress as function of strain rate
3.2 Superplastic deformation mechanisms
Optical microstructure reveals that after deforma- tion at 723 K and strain rate of 1×10－3 s－1, the grain size increases to 29.5 μm(Fig.5(a)) at true strain of 0.18, which is coarser than its initial size of 17.5 μm(Fig.1). This results from uniform heating of the specimen prior to the tensile test. Then grain size is further reduced to 22.5 μm(Fig.5(b)) as examined at true strain of 0.29, and the emergence of finer grains on the initial grain boundary implies that dynamic recrystallization occurs at this stage. The flow stress firstly experiences a hardening stage, followed by a relatively stable flow stage. As the higher strain rate sensitivity of superplastic materials accounts for a wider stable flow stage, a higher elongation to failure is obtainable. It is found that the formation and growth of cavities are associated with the increasing strain.
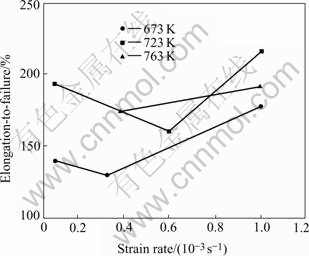
Fig.4 Variation in elongation-to-failure as function of strain rate
Cavities that are not observable in the initial microstructure (Fig.1) nucleate on grain boundary and at the boundary junctions in particular as strain increases
to 0.59 (Fig.5(c)). This is resulted from GBS which is the dominant mechanism in superplastic deformation. In GBS mode, although the stress concentration can be released by adjustment of diffusion and dislocation motion, cavities are likely to nucleate on grain boundary junctions when the sliding rate of GBS exceeds the limit within which the stress concentration can be accommodated. Fig.5(e) shows the microstructure of fracture, which consists of homogenous and equiaxial grains with mean grain size up to 55 μm. This is exactly the distinct characteristics of GBS, as it is evidenced by the fact that the grain size undergoes a marked growth, while remains uniform at the final stage of the deformation. There is also an obvious interlinkage of cavities at this stage.
Fig.6 shows the fracture surface of specimen deformed under the above mentioned condition. It is evident that the fracture surface is characterized by a combination of intergannular cracks and innergrannular dimples. The presence of cleavage steps indicates that GBS plays a pre-dominant role in the superplastic deformation of AZ31B sheet.
3.3 Cavity growth and interlinkage
The growth and connection of cavities were studied in detail by using SEM. SEM micrographs in Fig.7 show the longitudinal section of specimen (1.5 mm×6 mm×15 mm) deformed at 723 K and 1×10－3 s－1 true strains of 0.57, 0.73 and 0.96. Cavities are small in the initial nucleation stage (Fig.7(a)), and their growth is achieved by diffusion process. As the true strain increases to 0.73 (Fig.7(b)), cavities are elongated along the tensile axis. At this stage, the cavity growth is transitted to be controlled by the superplastic process of the matrix. With the increase of the true strain to 0.96 (Fig.7(c)), the expanding cavities link each other firstly along the longitudinal direction, then to orientation perpendicular to the tensile axis. Meanwhile, there are also secondary nucleation and expanding of cavities, and the cavitations became more severe with the increasing strain.
Fig.5 Microstructures after deformation at 723 K and strain rate of 1×10－3s－1 to different true strains: (a) 0.18; (b) 0.29; (c) 0.59; (d) 0.96; (e) Fracture
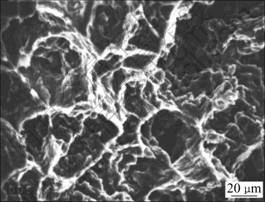
Fig.6 SEM fractograph of specimen after deformation at 723 K and strain rate of 1×10－3 s－1
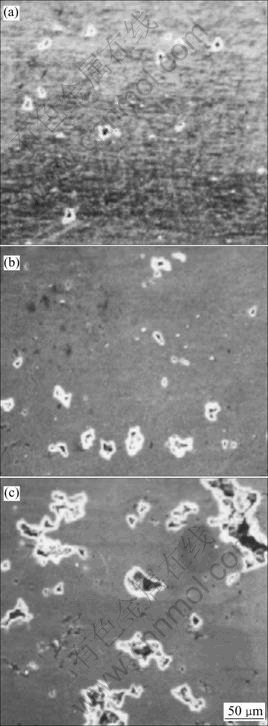
Fig.7 SEM micrographs showing longitudinal section of tensile specimen deformed at 723 K and 1×10－3 s－1: (a) ε=0.59; (b) ε=0.73; (c) ε=0.96
3.4 Cavity growth model
In order to have a quantitative study of cavity growth and connection of magnesium alloy sheet, cavity volume fraction and cavity radius were measured. SEM observation was conducted on the longitudinal section near the fracture site of tensile specimen deformed at 723 and 673 K with corresponding strain rate of 1×10－3 and 3.3×10－4 s－1 to varied strains. Cavity volume fraction and cavity radius measured in five observation views were calculated using self-developed cavity identification software, and their mean values were obtained for quantitative analysis.
Fig.8 shows the radius of cavities as function of true strain during superplastic deformation of AZ31B sheet. It can be seen that with the increasing strain, cavity radius increases gradually at the early stage before a rapid increase at the later stage in an exponential way.
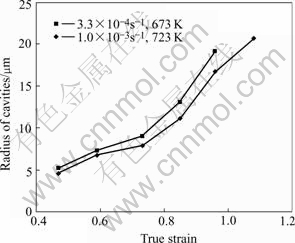
Fig.8 Radius of cavities as function of true strain during superplastic deformation
In reference to the growth model of cavity radius proposed by Rice-Tracey, the quantitative dependency of cavity radius(r) on true strain(ε) can be expressed by
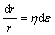(1)
where η is the cavity expanding coefficient related to alloys series, strain rate sensitivity(m) and stress ratio σm/σe.
Integrate Eqn.(1) yields
r=r0exp[η(ε-ε0)] (2)
where ε0 is the equivalent strain for cavity nucleation, and r0 is the initial cavity radius.
Gauss-Newton method was adopted in non-linear analysis of relation between cavity radius and true strain to determine the damage characteristic parameter r0 and η(Table 1) of AZ31B sheet under two deformation conditions.
3.5 Damage evolution equation
Many studies have revealed that the higher the damage variable(D) is, the greater the absolute release rate of damage strain energy(Y) is. Lemaitre proposed an empirical equation of damage evolution based on an experimental study of materials which has isotropic mechanical performance[17]:
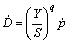(3)
where S and q are the constants dependent on materials and deformation conditions.
In Ref.[11], the dependency of release rate of damage strain energy(Y) on damage variable(D) is expressed as
(4)
where σm is the mean stress, σe is macro equivalent stress,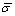 
is the matrix equivalent stress; A, B and r1 are the constants dependent on materials and deformation conditions.
According to the concept of effective stress put forward by Lemaitre, the effective stress of matrix in superplastic deformation can be expressed as
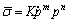(5)
where p is the accumulated superplastic strain,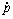 
is the superplastic strain rate, m is the strain rate sensitivity, n is the strain hardening coefficient, and K is the material constant.
In Ref.[11], the integral equation of damage evolution in superplastic metal is expressed as
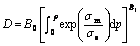(6)
where D is the damage variable, if D=0, the material is undamaged; if D=Dc, the material is damaged (Dc is the critical value of damage variable ); B0 and B1 are constants dependent on materials and deformation conditions. So long as B0 and B1 are determined with tensile test, it is able to obtain the damage variable D of superplastic deformation by any load paths.
Under proportional loading, the stain ratio is a constant, and stress ratio σm/σe is expressed as
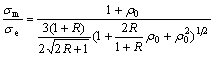(7)
where R is plastic strain ratio.
Hence σm/σe=constant, assumed that pD is the threshold of accumulated plastic strain, namely p＜pD. The integration of Eqn.(6) is
(8)
In tensile test, σm/σe=1/3, assumed that εf is the plastic strain at fracturing in tensile test, and that εD is the threshold of strain in tensile test. Eqn.(8) can be written as
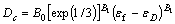(9)
where Dc is the critical value of damage variable.
3.6 Determination of material characteristic parameters in damage evolution equation
In superplastic deformation, cavity fraction volume(fv) is measured as damage variable, and material characteristic parameters B0 and B1 of AZ31B sheet are determined with tensile test.
If pD＝0, to have logarithm of Eqn.(8), cavity fraction volume is generally chosen as the damage variable, then
lnfv=B+B1lnp (10)
Or in unit-axis tensile state, Eqn.(10) can be written as
lnfv=B+B1lnε (11)
where B=lnB0+B1(σm/σe).
It is evident in Eqn.(10) that the slope of line lnfv—lnε and interception of the line on axis lnfv correspond respectively to the material characteristic parameter B0 and B1, which can be estimated with true strains and cavity volume fraction measured in tensile test of AZ31B sheet. Thus, critical value of damage variable Dc can be calculated with Eqn.(9). The damage characteristic parameters of AZ31B sheet under two kinds of thermodynamic conditions are listed in Table 1.
Table 1 Material characteristic parameters of AZ31B magnesium alloy during superplastic deformation
4 Conclusions
1) Industrial AZ31B sheet exhibits high ductility under a definite thermodynamic condition. Maximum elongation of 216% and strain rate sensitivity of 0.36 are obtained at 723 K and a strain rate of 1×10－3 s－1.
2) Many fine grains generates on the vicinity of original grain boundary via dynamic recrystallization, and the grain size increases with rising strain. The grain boundary sliding is the dominant deformation mode of superplastic AZ31B sheet, whose fracture was due to the growth and interlinkage of cavities that nucleate at grain boundary. Secondary nucleation and expanding of cavities took place at the same time when the original cavities clustered and coalesced.
3) A cavity growth model of AZ31B magnesium alloy sheet was established, and damage characteristic parameters as well as the critical value of damage variable were identified in an effort to provide a theoretical basis on which the plastic forming technology can be optimized, and the study on the superplastic instability and theoretical prediction of forming limit can also be further developed.
References
[1] LIU Zheng, WANG Yue. The research and application of magnesium based material[J]. Chinese Journal of Material Research, 2000, 14(5): 449-456.(in Chinese)
[2] Mordike b l, Ebert t. Magnesium properties—applications- potential[J]. Mater Sci Eng A, 2001, A302: 37-45.
[3] Aghion e, Bronfin b, Eliezer d. The role of the magnesium industry in protecting the environment[J]. Journal of Materials Processing Technology, 2001, 117: 381-385.
[4] Tan j c, Tan m j. Superplasticity in a rolled Mg-3Al-1Zn alloy by two-stage deformation method[J]. Scripta Materialia, 2002, 47: 101-106.
[5] Mabuchi m, Lwasaki h, Yanace k, Higashi k. Low temperature superplasticity in an AZ91 magnesium alloy processed by ecae[J]. Scripta Materialia, 1997, 36(6): 681-686.
[6] Mohri t, Mabuchi m, Nakamura m, Asahina t, Iwasaki h, Aizawa t, Higashi k. Microstructural evolution and superplasticity of rolled Mg-9AL-1Zn[J]. Mater Sci Eng A, 2000, A290: 139-144.
[7] YU Yan-dong, ZHANG Kai-feng. The superplasticity and superplastic bulk of the rolled magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(1): 71-75.(in Chinese)
[8] MA Hong-tao. The study on superplasticity of MB26 magnesium alloy[J]. Journal of Material Engeering, 1998, 9: 11-13.(in Chinese)
[9] LIU Man-ping, MA Chun-jiang. The superplastic deformation of Industrial AZ31B magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(4): 797-801.(in Chinese)
[10] XIN Wu, YI Liu. Superplasticity of coarse-grained magnesium alloy[J]. Scripta Materialia, 2002, 46: 269-274.
[11] WU Shi-chun The Theory of the Superplastic Deformation in Metal[J]. Beijing: National Defence Industrial Press, 1997. 103-172.(in Chinese)
[12] Bae d h, Ghosh a k. Cavity formation and early growth in a superplastic Al-Mg alloy[J]. Acta Materialia, 2002, 50: 511-523.
[13] Chow k k, chan k c. Effect of stress state on cavitation and hot forming limits of a coarse-grained A15052 alloy[J]. Materials Letters, 2002, 52: 62-68.
[14] Khaleel m a, Zbib h m, Nyberg e a. Constitutive modeling of deformation and damage in superplastic materials[J]. International Journal of Plasticity, 2001, 17: 277-296.
[15] Taylor m b, Zbib h m, khaleel m a. Damage and size effect during superplastic deformation[J]. International Journal of Plasticity, 2002, 18: 415-442.
[16] CHEN Pei-sheng, SUN Yang-shan, JIANG Jian-qing. The cavity in the SiC/MB2 cmposite under superplastic deformation on a high strain rate[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(1): 140-144.(in Chinese)
[17] YU Shou-wen, FENG Xi-qiao. Damage Mechanics[M]. Beijing: Tsinghua University Press, 1997. 47-58.(in Chinese)
Foundation item: Project(2001AA331050-3) supported by the Hi-tech Research Program of China
Corresponding author: WANG Ling-yun; Tel: +86-23-65103711; E-mail: cqulywang@yahoo.com.cn
(Edited by LONG Huai-zhong)
