DOI: 10.11817/j.issn.1672-7207.2015.08.043
简支槽型钢梁-混凝土曲线组合梁施工阶段扭转效应解析法研究
张彦玲1,刘玉玲1,李运生1,侯忠明2
(1. 石家庄铁道大学 土木工程学院,河北 石家庄,050043;
2. 清华大学 土木工程系,北京,100084)
摘要:采用M/r法将竖向均布荷载作用下梁轴曲率的影响等效为分布扭矩,并基于符拉索夫理论,采用初参数法计算曲线开口钢梁的扭转效应,分别通过离散法和连续法分析横隔板对其产生的影响。研究结果表明:采用离散法和连续法得到的截面扭转角和扭率非常接近,扭矩完全相同,但双力矩和翘曲应力在横隔板位置差别较大;增加横隔板对曲线开口钢梁的扭矩无影响,但使截面扭转角、扭率、双力矩和翘曲正应力均明显减小,翘曲正应力随横隔板数量N的增加非线性下降,随曲线跨度与半径比值的增大线性增长。离散法可明确反映横隔板的影响,但比连续法计算复杂;横隔板数量越多,2种方法的结果越接近。实际工程中的曲线组合梁桥,可采用连续法进行分析。
关键词:曲线组合梁;施工阶段;约束扭转;横隔板;M/r法
中图分类号:U448.21 文献标志码:A 文章编号:1672-7207(2015)08-3083-09
Analytical method research on torsion effect of simple curved channel steel girder-concrete composite beams in construction stage
ZHANG Yanling1, LIU Yuling1, LI Yunsheng1, Hou Zhongming2
(1. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;
2. Department of Civil Engineering, Tsinghua University, Beijing 100084, China)
Abstract: The curvature-induced effect under the vertical uniform load was dealt with equivalent distributed torsion moment by M/r method firstly, and then based on the Vlasov theory, the torsion behavior was calculated by initial parameter method, the diaphragm effect was analyzed by discrete method and continuous method respectively. The results indicate that for the discrete method and the continuous method, the section torsion angle and torsional curvature obtained by the two methods are very close to each other, and the torsion moments are the same entirely, but the double moment and wrap stress have lager differences at the position of diaphragms. Increasing diaphragm number has no influence on the torsion moment, but can make the section torsion angel, torsional curvature, double moment and wrap stress all decrease apparently, in which the warp stress decreases nonlinearly with the increase of diaphragm number, and increases linearly with the increase of the span-radius ratio increase. The discrete method can reflect the diaphragm effect apparently, but is more complicated than the continuous method; with the increase of the diaphragm number, the results of the two methods become much closer. For the curved composite beam bridges, the continuous method is more applicable.
Key words: curved composite beam; construction stage; restrained torsion; diaphragm; M/r method
钢-混凝土组合梁在公路、铁路和城市桥梁中已得到广泛应用,当其平面线型设计为曲线时,会在荷载作用下产生弯剪扭复合作用,因此通常选用由混凝土翼板和开口槽型钢梁组成的抗扭刚度较大的箱形截面,但在浇筑混凝土阶段,施工荷载仅由抗扭刚度较弱的开口槽型钢梁承担,易导致钢梁的过度扭转和横向连接系的过早屈服。为了提高曲线组合梁的抗扭刚度,需设置适当的横向连接系,国外通常采用支架式,即在钢梁顶部设置水平横撑,在内部设置斜撑,在多箱梁桥各箱之间设置外部横撑,而我国则主要采用箱内设横隔板的隔板式横向连接。目前,关于“支架式组合梁”施工阶段的受力特性[1-3]和“隔板式”闭口箱形组合梁及闭口箱形钢梁的横隔板间距已有部分研究[4-8];关于开口钢梁,目前对于工字型钢梁之间的横向连接系研究较多[9-12],但其作用机理与“隔板式组合梁”施工阶段开口槽型钢梁中的横隔板是不同的。后者横隔板的作用是对开口截面本身的刚度进行加强,使其抗扭刚度处于开口截面与闭口截面之间,而前者横向连接系只是将各根钢梁连接在一起,并不加强开口截面本身的刚度,因此二者受力机理不同。关于“隔板式组合梁”施工阶段开口槽型钢梁横隔板效应的相关研究还较少,横隔板设置方法在我国各种规范中也无具体规定。因此,本文作者以其为研究对象,首先采用M/r法将梁轴曲率的影响等效为分布扭矩,然后基于符拉索夫理论和初参数法求解其弯扭效应,最后分别通过离散法和解析法分析了横隔板所产生的影响,并对2种解析方法进行了比较。
1 M/r法求解曲梁内力
支架式横向连接和隔板式横向连接分别如图1和2所示。曲线组合梁在浇筑混凝土板过程中,可将混凝土湿重模拟为竖向均布荷载,完全由钢梁承受。竖向均布荷载作用下简支超静定曲梁的内力可采用结构力学的方法直接获得,但不便于分析横隔板效应对曲梁弯扭效应产生的影响。
M/r法是求解简支和超静定曲梁的一种实用简便的算法,其计算原理如图3所示。将竖向荷载作用下曲线开口钢箱梁的截面弯矩表示为作用于顶、底板上的一对大小相等,方向相反的轴力[13]。在梁中任意取出一个微段,当弯矩为正时,由于曲率的影响,微段两侧的切向拉力方向不同,因而产生了垂直于直线梁轴指向曲线内侧的横向作用力。同理,钢梁顶板会由于曲率的影响产生指向曲线外侧的大小相等的横向分布力。这样,梁轴曲率的影响就可等效为作用于曲梁上、下翼缘的反对称水平荷载,从而产生截面扭矩M/r。
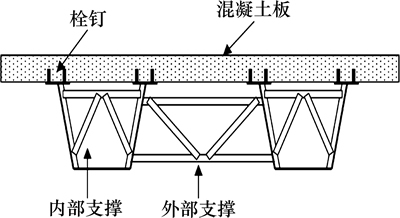
图1 支架式横向连接
Fig. 1 Transverse connection with cross bracing

图2 隔板式横向连接
Fig. 2 Transverse connection with diaphragms
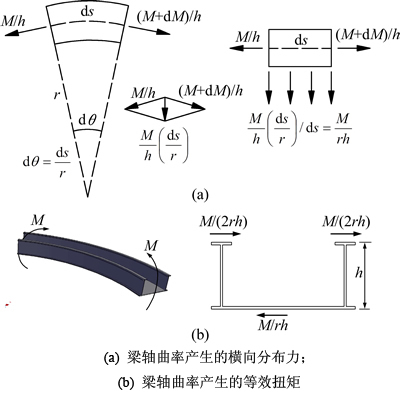
图3 M/r法计算原理
Fig. 3 Calculation principle of M/r method
采用M/r法计算曲梁扭矩[14]的步骤如下。
1) 将曲梁按中心线弧长展开为直梁,支承条件与原来的曲梁相同,计算此直梁在竖向荷载作用下的弯矩;
2) 将梁的弯矩除以曲线半径r,得到分布扭矩M/r;
3) 把2个约束扭转支座间的弧长l作为计算扭矩时的跨径,并假定直梁为简支支承,将扭矩M/r施加在此直梁上,求出的直梁的扭矩即为原曲梁的扭矩。
本文讨论的简支曲线组合梁及其截面如图4所示,两侧简支端均设置抗扭支座,属于简支超静定结构。沿梁轴方向设置若干横隔板,横隔板上方设上翼缘,与钢梁腹板上方的上翼缘同样焊接圆柱头焊钉,以便待混凝土结硬后与混凝土板结合成为组合截面。
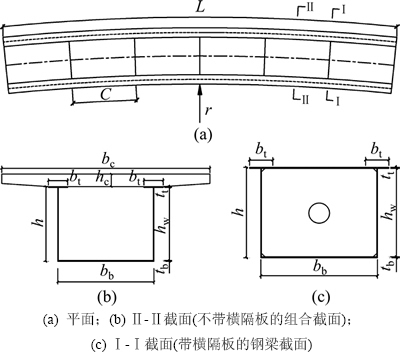
图4 曲线组合梁
Fig. 4 Curved composite beam
根据M/r法,将图4所示的曲梁展开为图5所示的直梁后,在均布荷载q作用下的弯矩M(z)为
 (1)
(1)
式中:z为沿梁轴向的纵坐标。
则M/r法中需施加于直梁上的分布扭矩m(z)为
 (2)
(2)
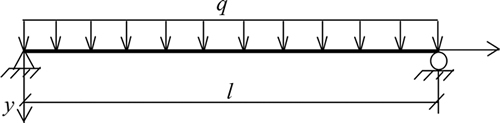
图5 M/r法等效直梁
Fig. 5 Equivalent straight beam in M/r method
2 采用初参数法求解分布扭矩作用下简支曲梁的扭转效应
根据符拉索夫理论,开口薄壁截面约束扭转微分方程为[15]
 (3)
(3)
其中: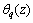 为荷载作用下截面
为荷载作用下截面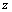 处的扭转角;E为钢梁弹性模量;
处的扭转角;E为钢梁弹性模量;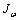 为截面的主扇性惯性矩;G为钢梁剪切模量;Jd为截面的自由扭转惯性矩(不考虑横隔板效应)。
为截面的主扇性惯性矩;G为钢梁剪切模量;Jd为截面的自由扭转惯性矩(不考虑横隔板效应)。
该微分方程可采用初参数法进行求解。荷载作用下梁中任意截面的状态向量可表示为
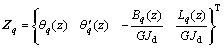 (4)
(4)
式中: 表示荷载作用下截面
表示荷载作用下截面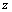 处的扭率;
处的扭率;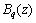 为荷载作用下截面z处的双力矩;
为荷载作用下截面z处的双力矩;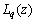 为荷载作用下截面z处的扭矩。
为荷载作用下截面z处的扭矩。
梁端铰支时,方程(4)的边界条件为:
当z=0时,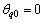 ,
, ;当z=l时,
;当z=l时,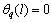 ,
,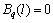 。
。
将纵向坐标z的原点z=0作为初始截面,则初始状态向量为
 (5)
(5)
在0≤z≤l之间有分布扭矩m(z),则0≤z≤l之间的分布状态向量 为
为
 (6)
(6)
则任意截面处的状态向量为
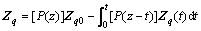 (7)
(7)
其中:[P(z)]和[P(z-t)]的表达式见文献[15]。
将式(6)代入式(7)的第2项,积分后和式(5)共同代入式(7),得:

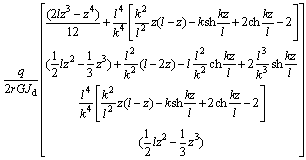 (8)
(8)
其中: 。
。
由z=l端的边界条件得:

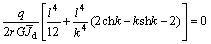

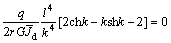
两式相减,得:
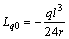 (9)
(9)
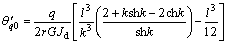 (10)
(10)
将 和
和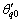 代入式(8),得竖向均布荷载q作用下的简支曲梁的各种荷载效应为:
代入式(8),得竖向均布荷载q作用下的简支曲梁的各种荷载效应为:

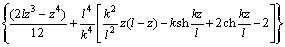 (11)
(11)

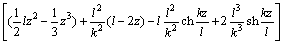 (12)
(12)
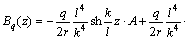
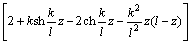 (13)
(13)
 (14)
(14)
式中: 。
。
3 采用初参数法求解横隔板对曲梁荷载效应产生的影响
在开口薄壁槽形钢梁中设置横隔板,可有效减小截面的翘曲程度,使抗扭刚度提高。对于图4中的曲梁,其横隔板效应可分为2部分,第1部分是横隔板本身的影响,第2部分是其上翼缘产生的横向联系作用,这2部分对曲梁产生的影响均可用2种方法进行处理:一种是单独计算每个横隔板及上翼缘的作用(离散化处理),另一种是进行连续化处理。
3.1 离散化处理
3.1.1 横隔板上翼缘
根据符拉索夫理论,在钢梁受扭时,由于截面发生翘曲,使隔板上翼缘在纵向平面内弯曲成S形,在其跨中形成反弯点。在z=ti处沿该反弯点将隔板上翼缘切开,得到一静定基本体系。此时在每个切口处产生一对多余未知力Qi(i=1,2,…,n),则由Qi在其自身平面内产生的双力矩为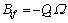 (Ω为截面外形轮廓线所围面积的2倍),即在每个隔板上翼缘处,相当于施加了一个约束双力矩。
(Ω为截面外形轮廓线所围面积的2倍),即在每个隔板上翼缘处,相当于施加了一个约束双力矩。
在外部扭矩和Qi的共同作用下,任一切口处的纵向相对位移应为0,可得如下力法方程:
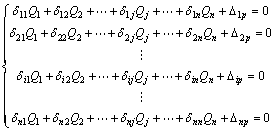 (15)
(15)
其中:Δip为由荷载引起的在第i个切口处沿Qi=1方向的纵向相对位移;δij为基本体系中第j块隔板上翼缘切口处作用有1对单位剪力Qi=1时,在第i块隔板上翼缘切口两侧所产生的沿Qi方向的纵向相对位移;δii表示第i块隔板上翼缘切口处作用有1对单位剪力Qi=1时,在该切口两侧所产生的纵向相对位移。
两端铰结时,方程(15)中的系数与常数项为[15]:
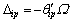 (16)
(16)
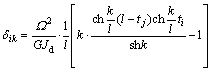 (17)
(17)
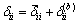 (18)
(18)
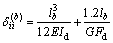 (19)
(19)
其中:tk和ti分别为第j块和第i块横隔板位置沿梁轴的坐标;lb为隔板上翼缘长;  ,
,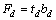 ,td为隔板上翼缘厚,bd为隔板上翼缘宽。
,td为隔板上翼缘厚,bd为隔板上翼缘宽。
对于图1所示的曲梁,当沿梁轴设置5块横隔板时(z1=0,z2=l/4,z3=l/2,z4=3l/4,z5=l)时,由式(16)~(19)可得力法方程(15)中的系数与常数项,并对方程求解后可得:
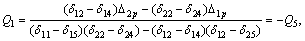
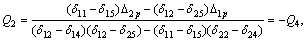
 ,则:
,则: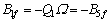 ,
, 
 ,
,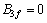 。
。
3.1.2 横隔板
当z=ti处作用有1块横隔板时,也可将其效应模拟为在该处作用一双力矩[15]:
 (20)
(20)
当隔板周边固结时,
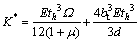 (21)
(21)
其中:th为隔板的厚度;d为槽形截面的腹板间距;bt为钢梁上翼缘宽度;E材料弹性模量,μ为泊松比。
同样,对于图4所示的曲梁,当沿梁轴设置5块横隔板时,由式(20)可得:


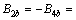

 。
。
则每个隔板处产生的总约束双力矩为: (i=1,2,…,5)。
(i=1,2,…,5)。
3.1.3 采用离散法和初参数法分析横隔板效应
根据图4,以沿梁轴设置五块横隔板为例,设纵向坐标z的原点在z=0处,并将其作为初始截面,则初始状态向量为
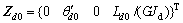
在zi(i=1,2,…,5)处有双力矩Bi作用,则zi处的状态向量为
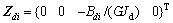
于是双力矩作用下任意截面的状态向量为
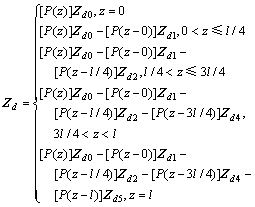
在z=l处,有: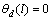 ,
, 。
。

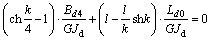 ,
,
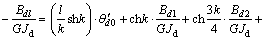
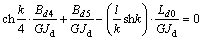 。
。
联立解得:
 ,
,
 。
。
则由横隔板产生的双力矩引起的薄壁钢梁的扭转角、扭率、双力矩和扭矩沿梁轴的分布为如下。
当0≤z≤l/4时,
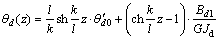 ,
,
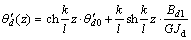 ,
,
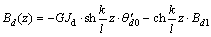 ,
,
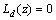 。
。
当l/4<z≤l/2时,

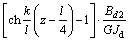 ,
,
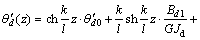
 ,
,
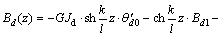
 ,
,
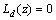 。
。
其中:扭转角和双力矩图形对跨中对称;扭率和扭矩图形对跨中反对称。
3.2 连续化处理
对于用隔板加强的槽形截面薄壁杆件的约束扭转,若开口截面杆件中包含多层隔板,而且这些隔板沿杆长均匀布置,则可将它们进行连续化处理,用一个等效连续弹性介质来代替,形成“准闭口截面”。采用连续化处理后,由于横隔板及其上翼缘的横向连接作用,“准闭口截面”的抗扭刚度增大,其中由隔板上翼缘所产生的附加抗扭刚度为
 (22)
(22)
其中:lb为隔板上翼缘长;C为隔板上翼缘中心间距;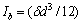 ;
;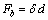 ;
;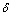 为隔板上翼缘厚;d为隔板上翼缘宽。
为隔板上翼缘厚;d为隔板上翼缘宽。
由横隔板所产生的附加抗扭刚度为
 (23)
(23)
这样,采用横隔板及其上翼缘进行加强的开口薄壁杆件,其约束微分方程可由式(3)转变为
 (24)
(24)
其中: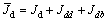 。
。
令 ,则可采用初参数法对式(24)进行求解。
,则可采用初参数法对式(24)进行求解。
4 曲线组合梁施工阶段钢梁的横隔板效应
4.1 算例
某曲线组合梁计算跨度l=6 m,曲线半径r=30 m,跨径比l/r为0.2,截面如图4所示。钢梁采用Q235钢,上翼缘宽度bt=60 mm,厚度tt=8 mm;腹板高度hw=184 mm,厚度tw=6 mm;下翼缘宽度bb=370 mm,厚度tb=8 mm。沿轴向设置5块横隔板,横隔板及其上翼缘厚6 mm,上翼缘宽50 mm。桥面板采用C30混凝土,宽度bc=700 mm,厚度hc=70 mm。浇筑混凝土阶段的承载结构为开口薄壁钢梁。
钢梁截面主扇性惯性矩Jω=8.167 4×1011 mm6;自由扭转惯性矩Jd=1.112 7×105 mm4,横隔板参数K*=1.540 2×1012 N·mm3。隔板上翼缘附加抗扭刚度为Jdb=1.086×106 mm4,隔板附加抗扭刚度Jdd=0.013×105 mm4,考虑横隔板强化后的整体扭转刚度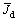 =1.211×106 mm4。混凝土自重下的均布荷载q=1.225 N/mm。
=1.211×106 mm4。混凝土自重下的均布荷载q=1.225 N/mm。
将离散法中的横隔板效应与荷载效应叠加得到的总效应,以及仅在荷载作用下(相当于无隔板作用)的效应及采用连续化处理后的结果见图6。
由图6可知:1) 与无隔板相比沿梁轴设置5块横隔板后,截面的扭转角、扭率和双力矩均明显减小,但对扭矩无影响;2) 采用离散法和连续法所得的扭转角、扭率非常接近,扭矩完全相同,但双力矩只在跨中区域比较接近。采用离散法计算时,由于将每个横隔板及其上翼缘均看作一个集中双力矩的作用,因此在横隔板位置双力矩图发生突变,尤其是在简支曲梁支点位置,由于将端横隔板的作用也模拟为一个集中双力矩,故支点处双力矩也不为0 kN·m2,与连续法差别较大。
4.2 横隔板效应对截面翘曲正应力的影响
曲梁在双力矩作用下,在截面中产生约束扭转翘曲正应力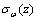 为
为
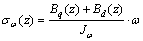 (25)
(25)
式中:ω为角点1的扇性坐标,在本文算例中,ω=17 543.53 mm2。
以算例为原型,变化横隔板数N,分别考虑沿梁轴共设2,3,5,9块横隔板,则不同横隔板数时的横隔板间距C、隔板上翼缘附加抗扭刚度Jdb、隔板附加抗扭刚度Jdd以及考虑横隔板强化后的整体扭转刚度 如表1所示。
如表1所示。
不同横隔板数时,分别由离散法和连续法得到的图4中曲线外侧钢梁下翼缘与腹板相交处(角点1)的翘曲正应力如图7所示。
由图7可知:1) 采用连续法和离散法时角点1的翘曲应力均随横隔板数的增加明显下降,但与5块隔板相比,采用9块横隔板时翘曲应力的下降不明显;2) 采用离散法时,在横隔板位置翘曲应力发生突变;由于跨中截面扭率为0 m-1,故跨中横隔板不起作用,2块隔板和3块隔板时翘曲应力曲线重合。与连续法相比,中横隔板位置处离散法结果在连续法结果的上下波动,但跨中区域二者翘曲应力接近;3) 横隔板数越多,2种方法的计算结果越接近。
表1 不同横隔板数时的自由扭转惯性矩
Table 1 Free torsion constant for different diaphragm numbers
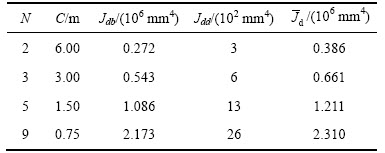
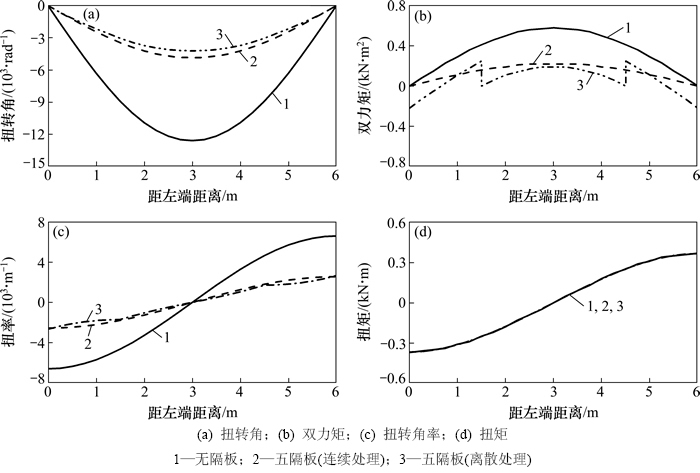
图6 五隔板和无隔板简支曲梁的荷载效应
Fig. 6 Load effects of simple curved beam with five diaphragms and without diaphragms
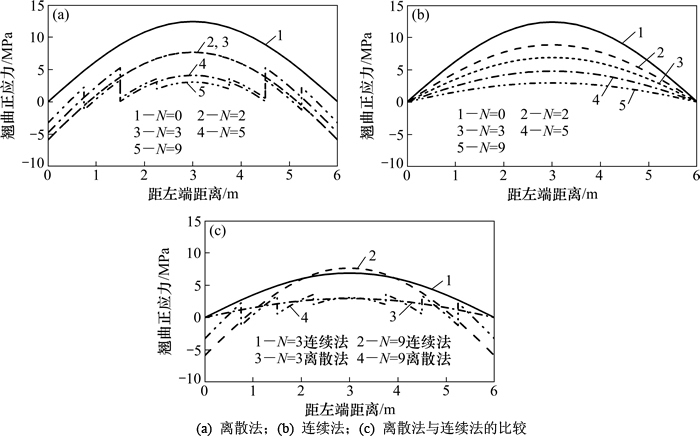
图7 不同横隔板数时简支曲梁的翘曲正应力
Fig. 7 Wrap stress of simple curved beam with different diaphragm numbers
取出跨中截面角点1的翘曲正应力进行研究,其与横隔板数N的关系如图8所示。
由图8可知:角点1翘曲应力随横隔板数的增加而下降;采用连续法计算时,当N从0增加到3时翘曲应力线性下降,当N大于3后非线性下降,下降幅度减缓;采用离散法计算时,当N从0增加到2时翘曲应力下降,但N=2和N=3时翘曲应力相同,按照离散法的原理跨中横隔板在曲梁承受对称荷载时对扭转效应没有影响,N大于3后翘曲应力变化规律与连续法相同。
取跨径比分别为0.1,0.2,0.3,0.4,0.5,得到连续法算得的角点1翘曲应力与跨径比的关系如图9所示。由图9可知:不同横隔板数下,角点1翘曲正应力均随跨径比的增加线性增长,说明跨径比是曲梁扭转效应的显性指标。
图8 角点1翘曲正应力随横隔板数的变化
Fig. 8 Change of wrap stress of point 1 with diaphragms number
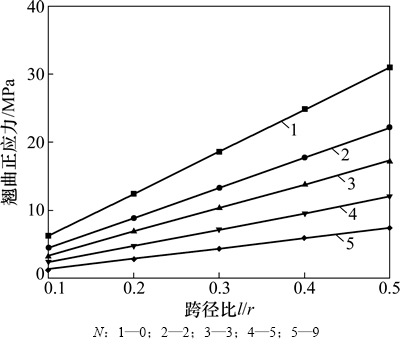
图9 角点1翘曲正应力随跨径比的变化
Fig. 9 Change of wrap stress of point 1 with span-radius ratio
5 结论
1) 可分别采用离散法和连续法对隔板式曲线组合梁施工阶段开口钢梁的横隔板效应进行计算。离散法将每块横隔板效应模拟为一个集中双力矩,可明确反映横隔板的影响,但计算比较复杂;连续法将横隔板效应处理为截面的附加扭转刚度,计算较方便,但不能反映横隔板附近位置力学性能的突变。横隔板数越多,2种方法得到的结果越接近。因此,对于实际工程中横隔板数较多的曲线组合梁桥,可采用计算较为方便的连续法进行分析。
2) 离散法和连续法得到的截面扭转角和扭率非常接近,扭矩完全相同。采用离散法时,均布荷载作用下跨中横隔板对曲梁的扭转效应没有影响,其他中横隔板位置处的双力矩和翘曲应力在连续法结果的上下波动,但跨中区域二者结果接近。无论采用哪种方法,设置一定数量的横隔板后,曲线开口钢梁的截面扭转角、扭率、双力矩和截面翘曲正应力均明显减小,但对扭矩无影响。
3) 采用离散法和连续法得到的截面翘曲正应力均随横隔板数N的增加而非线性下降,随跨径比的增大而呈线性增长。
参考文献:
[1] Davidson J S, Keller M A, Yoo C H. Cross frame spacing and parametric effects in horizontally curved I-girder bridges[J]. Journal of Structural Engineering, 1996, 122(9): 1089-1096.
[2] Kim K, Yoo C H. Brace forces in steel box girders with single diagonal lateral bracing systems[J]. Journal of Structural Engineering, 2006, 132(8): 1212-1222.
[3] Kyungsik K, Chai H Y. Bending behaviors of quasi-closed trapezoidal box girders with X-type internal cross-frames[J]. Journal of Constructional Steel Research, 2009, 65(8/9): 1827-1835.
[4] Park N H, Choi Y J, Kang Y J. Spacing of intermediate diaphragms in horizontally curved steel box girder bridges[J]. Finite Elements in Analysis and Design, 2005, 41(9/10): 925-943.
[5] 李海锋, 罗永峰. 横隔板对薄壁钢箱梁纵向正应力的影响[J]. 建筑结构学报, 2009(S1): 39-44
LI Haifeng, LUO Yongfeng. Influences of diaphragms of thin-walled box steel beams on the longitudinal normal stress[J]. Journal of Building Structures, 2009(S1): 39-44.
[6] 卫星, 李俊, 强士中. 扁平钢箱梁横隔板非线性稳定分析[J]. 中国铁道科学, 2009, 30(4): 30-35.
WEI Xing, LI Jun, QIANG Shizhong. Nonlinear stability analysis on the diaphragm plate of flat steel box girder[J]. China Railway Science, 2009, 30(4): 30-35.
[7] 赵甲荐, 魏德敏. 单箱双室箱梁横隔板与横隔墙剪切应变能计算[J]. 华南理工大学学报(自然科学版), 2010, 38(11): 47-53.
ZHAO Jiajian, WEI Demin. Calculation of shear strain energy for diaphragms and side walls of single-box double-cell box girder[J]. Journal of South China University of Technology (Natural Science Edition), 2010, 38(11): 47-53.
[8] 叶华文, 管乐, 卫星. 运营阶段大跨斜拉桥扁平钢箱梁横隔板受力分析[J]. 重庆交通大学学报(自然科学版), 2011, 30(2): 204-208.
YE Huawen, GUAN Yue, WEI Xing. Static behavior analysis of diaphragm in flat steel box girder of cable-stayed bridge in service stage[J]. Journal of Chongqing Jiaotong University (Natural Science), 2011, 30(2): 204-208.
[9] Jerome F H, Dan K, Luis P. Measured behavior of a curved composite I-girder bridge[J]. Journal of Constructional Steel Research, 2010, 66: 351-368.
[10] Park Y M, Hwang S Y, Hwang M O, et al. Inelastic buckling of torsionally braced I-girders under uniform bending: I. Numerical parametric studies[J]. Journal of Constructional Steel Research, 2010, 66: 304-316.
[11] Nguyen C T, Moon J, Le V N, et al. Lateral-torsional buckling of I-girders with discrete torsional bracings[J]. Journal of Constructional Steel Research, 2010, 66: 170-177.
[12] Joo H S, Moon J, Choi B H, et al. Rotational capacity and optimum bracing point of high strength steel I-girders[J]. Journal of Constructional Steel Research, 2013, 88: 79-89
[13] Fan Z F, Helwig T A. Distortional loads and brace forces in steel box girders[J]. Structural Engineering, 2002, 128(6): 710-718.
[14] 吴西伦. 弯梁桥设计[M]. 北京:人民交通出版社, 1990: 19-23.
WU Xilun. Design of curved bridges[M]. Beijing: China Communications Press, 1990: 19-23.
[15] 包世华, 周坚. 薄壁杆件结构力学[M]. 北京:中国建筑工业出版社, 2006: 174-193.
BAO Shihua, ZHOU Jian. Structural mechanics of thin-walled members[M]. Beijing: China Architecture & Building Press, 2006: 174-193.
(编辑 赵俊)
收稿日期:2014-08-15;修回日期:2014-11-10
基金项目(Foundation item):国家自然科学基金资助项目(51108281);河北省自然科学基金资助项目(E2014210038);河北省高等学校科学技术研究项目(ZD2014025);中国博士后科学基金资助项目(2014M560088)(Project (51108281) supported by the National Natural Science Foundation of China; Project (E2014210038) supported by the Natural Science Foundation of Hebei Province; Project (ZD2014025) supported by the Key Topics of Science and Technology Research Progam for Colleges and Universities of Hebei Province; Project (2014M560088) supported by the Postdoctoral Science Foundation of China)
通信作者:李运生,博士,教授,从事组合结构、桥梁结构理论及应用研究;E-mail:liysh70@163.com