DOI:10.11817/j.ysxb.1004.0609.2021-42029
基于不均匀块度分布的崩落矿岩流动特性研究
孙 浩1, 2,朱东风1, 2,金爱兵1, 2,尹泽松1, 2
(1. 北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京 100083;
2. 北京科技大学 土木与资源工程学院,北京 100083)
摘 要:为揭示不均匀块度分布条件下的崩落矿岩运移演化机理,开展矿岩散体流动特性物理与数值试验研究。从放出体形态变化规律和矿岩散体空隙率、平均配位数及其概率分布等方面对不同块度级配和堆积体系下的崩落矿岩流动特性进行了量化研究。研究结果表明:1) 在所研究的不同散体块度级配取值范围内,散体平均粒径越大则放出体最大宽度越大。2) 矿岩散体堆积体系的空隙率随高度的增大而增大,颗粒平均配位数均随高度的增大而减小。颗粒平均配位数的概率分布符合高斯分布,峰值范围内的颗粒平均配位数约为7~11。3) 随着散体堆积状态由自然堆积向密实堆积转变,散体堆积体系结构的各向异性程度变大,放矿所得放出体形态由倒置水滴形转变为正置水滴形,放出体最大宽度变小。研究结果可为建立基于矿岩颗粒体系结构特征的统一放出体形态表征模型提供有力支撑。
关键词:放矿;不均匀块度;堆积方式;崩落矿岩;流动特性;刚性块体模型
文章编号: 中图分类号:TD85 文献标志码:A
崩落法矿山开采过程中由爆破作用或自然崩落形成的矿岩一般是由许多大小不同、形状各异和排列复杂的不规则散体介质组成,其块度分布具有明显的不均匀性。传统的放矿理论和已有的绝大多数放矿试验研究均是以单一或均匀块度分布的矿岩散体作为试验介质,并未充分考虑实际崩落矿岩块度级配和空间分布(堆积状态)的不均匀性对放矿过程和结果的影响,进而导致采场结构参数设计与矿石贫损指标预测不甚合理[1]。因此,探究不均匀块度分布对崩落矿岩流动特性的影响十分必要。
长期以来,国内外学者基于单一或均匀分布的矿岩颗粒开展了大量室内放矿试验和数值试验研究。Peters[2]构建了同时期最大的二维放矿物理模型,通过放矿试验研究了放矿口尺寸对放出体形态的影响。Power[3]、Castro等[4]以砾石为介质,开展系统的三维物理放矿试验,研究了三维条件下放出体形态变化规律和矿岩流动规律。吴爱祥等[5]、孙浩等[6, 7]分别基于PFC3D程序构建均匀块度分布的矿岩散体模型,探究了无底柱分段崩落法结构参数优化、不同端壁条件以及不同散体介质条件下的放出体形态及最优崩矿步距等。陈庆发等[8]基于PFC2D程序开展柔性隔离层下散体介质流力链演化特征的数值试验,结合接触力学及统计力学相关知识,对多漏斗放矿过程中散体介质体系内力链长度、数量、强度、方向和准直系数等演化特征进行了量化研究。
目前,有关散体介质粒径或块度分布不均匀性的研究主要集中在公路堆石料、粉尘粒径等领域[9-11]。郑钢镖[12]、祝杰[13]分别运用R-R(Rosin-Rammler)分布函数探究了粉尘和喷淋塔内液滴中的粒径分布规律。而在放矿领域,李昌宁等[14]从影响矿岩散体的非均匀度的三个因素(粒径离散系数、空间分布离散系数和孔隙分布离散系数)出发,研究崩落矿岩散体的非均匀度,运用模糊综合评判决策得出三因素的定义、表达式及其与散体非均匀度的定量关系。李响等[15]基于实测节理面空间几何参数,使用蒙特-卡罗模拟某大型镍矿。
矿区节理空间分布,预测了矿岩等效尺寸。Castro等[16]通过多口放矿室内试验探究了同一矿岩散体级配条件和不同放矿方式下底部结构所承受垂直应力的变化规律,结果表明:放矿过程中垂直应力的变化范围为初始竖向应力的0.3~2.8倍,且与放矿方式和采场中的空间位置等因素密切相关。王洪江等[17]采用相似比为1: 100的放矿物理模拟试验,将矿样破碎后按粒级组成分为两组,初步探究了矿岩大块含量对放出体形态、孔口堵塞等放矿过程和结果的影响。张锦旺等[18]采用物理模拟试验和理论分析相结合的方法探究了块度级配对初始放煤量、颗粒运移轨迹以及煤岩分界面演化特征的影响,并基于散体介质力学理论推导了支架侧和采空区侧初始煤岩分界面动态演化方程,结合放煤试验结果确定了不同顶煤块度级配条件下煤岩分界面理论方程的修正系数取值。任凤玉等[19]设计放矿条件下尾砂穿流特性试验,以矿岩散体高度和尾砂高度作为影响因素,采用高速摄影技术,实现尾砂移动过程的可视化并研究了尾砂的移动规律,为类似矿山尾砂干排塌陷区提供借鉴。李涛[20]基于LBM-DEM耦合框架的单漏斗放矿模型,分别设置最大粒径和最小粒径为1.25 m和0.5 m,模拟了散体矿岩块度对放矿的影响。柳小波等[21]通过建立非均匀散体碰撞运动二维模型,模拟了非均匀散体流动过程。Hao等[22]基于PFC程序提出不规则颗粒簇的生成方法,探究了考虑二次破裂条件下的放出体形态和崩落矿岩块度的变化规律。
目前,已有文献中绝大多数放矿物理试验和数值模拟研究仅考虑了矿岩颗粒块度的差异性,并未充分考虑崩落矿岩空间分布的非均匀性对放矿结果的影响。本文综合采用物理试验、数值模拟和理论分析等手段,从矿岩颗粒块度级配和空间分布的不均匀性两方面对崩落矿岩流动特性进行探究,研究结果是对现行放矿理论的有益补充和完善,可为地下矿山结构参数优化、贫损指标预测以及矿产资源的安全高效开采提供理论与技术支持。
1 放矿物理试验研究
首先利用物理试验手段研究崩落矿岩块度级配这一因素对放出体形态变化的影响,并为后续基于细观离散单元法的放矿数值试验研究提供对照数据。
1.1 物理试验模型与材料
相似材料试验采用如图1所示全长高度为2.5 m的三维底部放矿物理试验模型,相似比为1: 25。为方便观察矿岩散体装卸情况,故模型正面材质选用可拆卸的半透明有机玻璃板;模型其余部分使用材质相对较轻且强度较大的聚氯乙烯(Polyvinyl Chloride,PVC)。为更准确反映实际采场边壁,模型四周的内壁均被打毛以增加其粗糙程度。模型内可装填尺寸为长×宽×高=0.8×0.8×2.0 m3;放矿口位于模型底部的中心位置,其尺寸为0.12×0.12 m2,可用于无限边界条件下的放矿物理试验研究。
考虑到本次物理试验所需散体材料总量较大,且大量物理与数值试验研究[3, 7, 23]已证实:在一定散体密度取值范围内,散体材料的类型对放矿过程与结果无显著影响。因此,在保证试验结果有效性的同时,为降低试验操作强度,本次物理试验中散体材料(图2(a)~(d))及标志颗粒(图2(e))均选用密度相对较小且易得的建筑用石灰石散体替代真实矿岩散体。试验前对散体材料进行粒径筛分,并对标志颗粒进行涂色与标号。其中,考虑到块度小于3 mm的近似粉末状颗粒不能准确表征绝大多数真实矿岩的形状与内锁力(Interlocked Force)等物理力学特性,且难以完全回收,故筛分过程中舍弃了块度为0~3 mm的散体材料。

图1 三维底部放矿物理模型
Fig. 1 The 3D physical model of bottom draw

图2 不同块度石灰石颗粒及标志颗粒
Fig. 2 Limestone particles of different size and labeled markers
1.2 物理试验方案设计
本次放矿物理试验基于散体介质研究领域最常用的罗辛-拉姆勒(Rosin-Rammler)分布函数(式(1))设计如图3所示不同散体块度级配的细颗粒组、中颗粒组和粗颗粒组共三组单口底部放矿试验。基于控制变量原则,每组试验相似比均为1: 25,所用散体材料块度级配的不均匀性系数[14]Cu均保持为2.60不变,平均块度D50分别为11.5 mm、14.9 mm和19.2 mm。
 (1)
(1)
式中:F(D)为粒径小于D的累积质量分数;D为颗粒粒径,mm;D50为平均块度,mm;Cu为不均匀性系数。
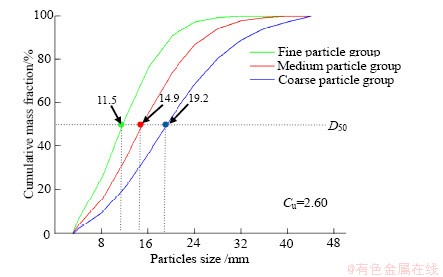
图3 放矿物理试验中不同颗粒块度级配曲线
Fig. 3 Particle size distribution curves in physical draw tests
三组试验除散体块度级配不同之外,其余试验条件与试验过程均相同。具体而言,本次试验采用标志颗粒法圈定放出体形态,标志颗粒布设方式均为如图2(e)所示,试验中采用中心四分法[24]装填矿岩散体,确保不同块度矿岩散体在整个模型内空间位置分布的均匀性;通过在模型顶部补充散体材料的方式保持每组试验中颗粒装填总高度以及最终放矿高度为2.0 m,模拟实际50 m的矿岩层高度和放矿高度;此外,为更准确模拟实际采场出矿过程,试验中尽量保持出矿时间间隔和单次出矿量等参量一致,最大限度降低人为因素对放矿物理试验结果的影响。
1.3 物理试验结果分析
在对放出标志颗粒以及放出散体材料总质量进行统计分析的基础上,利用Matlab软件中的均分计算指令对不同放出质量时的放出体最大宽度进行线性插值,圈绘得到如图4所示的三组放矿物理试验所得放出体形态纵剖面图;计算不同高度时放出体的最大半径,得到如图5所示的三组放矿物理试验所得放出体高度与其最大半径的拟合曲线。由图4和图5可知:不同散体块度级配的三组物理试验所得放出体形态均呈倒置水滴形,放出体高度与其最大半径之间均满足倒置水滴理论[25]所述幂函数关系(式(2)),拟合优度R2均大于0.996:
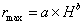 (2)
(2)
式中:rmax为放出体的最大半径,m;H为放出体的高度,m;a和b为拟合系数。
此外,如图4和图5所示,当放矿高度较小时,三组放矿试验所得放出体最大宽度基本一致,放矿口为其主要影响因素;而当放矿高度较大即远离放矿口时,相同放矿高度时的粗颗粒组(蓝色曲线)放矿试验所得放出体最大宽度略大,中颗粒组(红色曲线)次之,细颗粒组(黑色曲线)放矿试验所得放出体最大半径最小。由于三组放矿物理试验的试验方法、试验过程以及散体材质、不均匀系数等条件均相同,仅散体平均粒径这一因素不同,故在所研究的取值范围内,可以认为一定放矿高度条件下,散体平均粒径越大则放出体最大宽度越大,该结论与Castro[26]、Pierce[27]等学者的研究结果一致。由上述试验结果合理推测:三组试验中散体平均块度的差异不仅直接表现为粒间抗压、抗剪等内锁力(咬合力)的不同[26],也将导致散体堆积体系构型状态量(空隙率和配位数)的差异,即散体平均块度越大,其堆积体系的空隙率越大、配位数越小,散体越容易产生流动。下文将利用数值试验手段从放出体形态变化规律和矿岩散体空隙率、平均配位数及其概率分布等方面对不同堆积体系(不同颗粒空间分布非均匀性)条件下的崩落矿岩流动特性进行了量化研究。
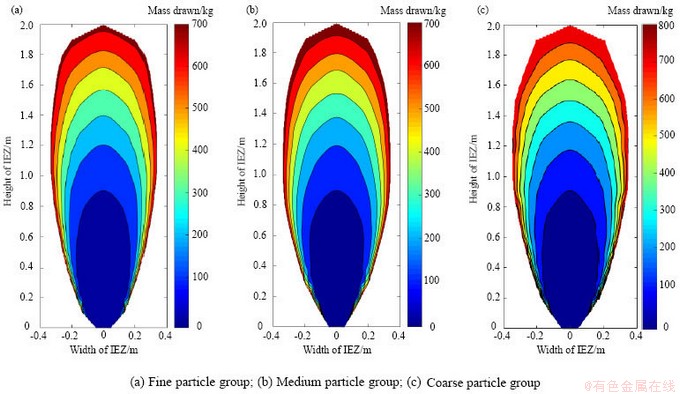
图4 三组放矿物理试验所得放出体形态纵剖面图
Fig. 4 Longitudinal profiles of the IEZ’s shapes in three physical draw tests
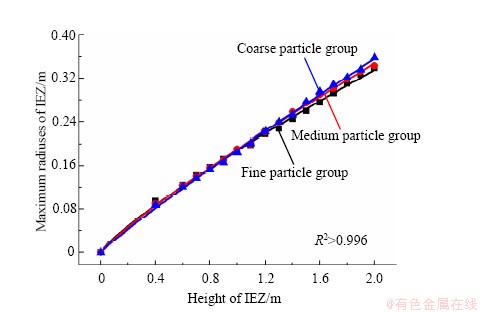
图5 三组放矿物理试验所得放出体高度与最大半径拟合曲线
Fig. 5 Fitting curves between the height and maximal radius of IEZ in three physical draw tests
2 放矿数值试验研究
针对国内外崩落法矿山而言,崩落矿岩的不均匀块度分布不仅表现为散体块度本身的差异性,亦涉及不同块度崩落矿岩在空间分布(堆积状态)上的非均匀性。在利用放矿物理试验研究不同散体块度级配对放出体形态变化影响的基础上,开展不同矿岩颗粒堆积体系下的放矿数值试验研究。
2.1 数值试验方案设计
众所周知,自然崩落法矿山在放矿过程中普遍存在自然破裂(Natural Fragmentation)、初次破裂(Primary Fragmentation)和二次破裂(Secondary Fragmentation)等现象[28],进而在高度上呈现出如图6[22]所示矿岩块度自上而下逐渐减小的情况;针对矿石强度大、岩石强度小的崩落法矿山,或者针对尾矿堆存和塌陷区占用土地资源的问题,任凤玉等[19]提出的放矿条件下尾砂干排至活动地表塌陷区的思路等,会在一定采场高度上出现矿岩块度“上小下大”的现象;此外,由于爆破对已有崩落矿岩的冲击压密作用,或者崩落矿岩长期堆积造成的不断压密现象等,亦会在采场中形成不同堆积密度或空隙率的矿岩散体堆积体系。
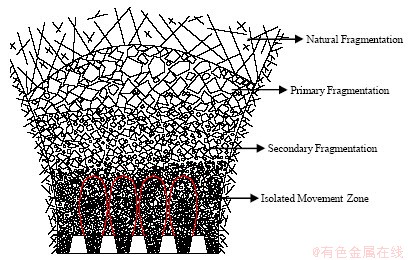
图6 自然崩落法中的矿岩破裂过程示意图[22]
Fig. 6 Schematic of fragmentation processes of caved ore and rock in block caving method[22]
基于此,共开展如图7所示的四组放矿数值试验,探究不同块度散体空间分布状态下的崩落矿岩流动特性。具体而言,四组放矿数值试验的颗粒块度级配均设计与图3中红色曲线所示中颗粒组的块度级配一致,并考虑放矿物理试验1: 25的相似比。因此,放矿数值试验中的颗粒块度级配如表1所示,其平均块度D50=0.0149 m×25=0.3725 m。其中,试验1设计与中颗粒组放矿物理试验一致,即不同块度的颗粒在高度上自然堆积且均匀分布(图7(a)),用以检验放矿数值模型的可靠性;作为对照,试验2中不同块度的颗粒在高度上密实堆积且均匀分布(图7(b));而试验3和试验4中不同块度颗粒的空间分布自上而下分别设计为依次减小(图7(c))和依次增大(图7(d))的两种自然堆积方式。
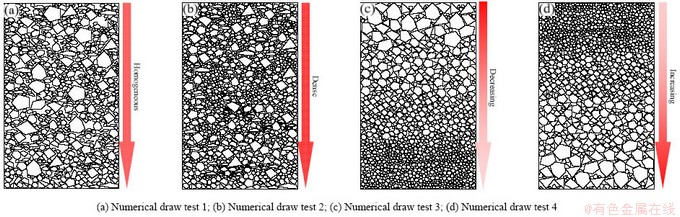
图7 不同崩落矿岩空间分布状态下的四组放矿数值试验设计示意图
Fig. 7 Schematic of four numerical draw tests under different spatial distributions of caved ore and rock
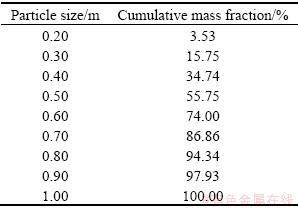
表1 四组放矿数值试验中的颗粒块度级配
Table 1 Particle size distributions in four numerical draw tests
2.2 数值试验过程
为降低四周边界效应对放矿过程的影响,本次放矿数值试验模型(图8)的尺寸为长×宽×高=30×30×50 m3;球形颗粒表面过于光滑而无法提供颗粒间足够的内锁力[29],故本次模拟采用PFC软件中的刚性块体模型(Rigid Block Model)[30]生成三棱锥型、对称型和细长型共三种不规则刚性块体模拟典型真实矿岩散体形状,并根据表1所示颗粒块度级配确定四组数值试验中所用不同块度的刚性块体数量。
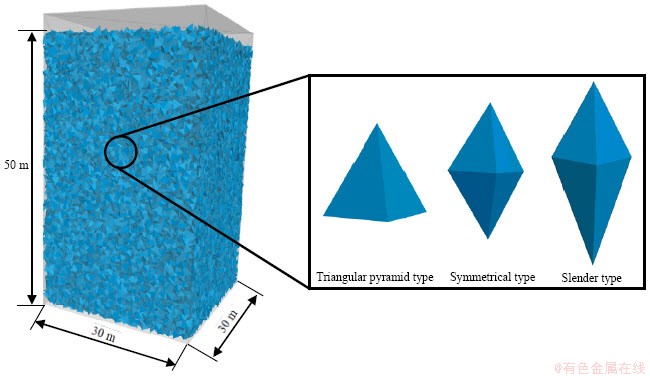
图8 放矿数值试验模型
Fig. 8 Model used in numerical draw tests
每组放矿数值试验开始前,首先统计并计算初始颗粒静态堆积体系中不同高度的空隙率(Void ratio)和颗粒平均配位数(Average coordination number);放矿过程中,通过编译FISH程序实时反演不同时刻的放出体形态,统计其高度和最大宽度等信息;其余模拟过程均与1.2节所述放矿物理试验过程保持一致,当放矿高度达50 m时停止出矿。四组放矿数值试验中墙体与刚性块体的细观参数取值见表2。
表2 墙体与刚性块体细观参数
Table 2 Meso-parameters of walls and rigid blocks

2.3 数值试验结果分析
四组放矿数值试验结束后,从放出体形态变化规律和矿岩散体空隙率、平均配位数及其概率分布等方面对比分析不同颗粒堆积体系下的崩落矿岩流动特性。
(1) 放出体形态变化规律分析
为了提高运算效率,本次数值试验中均利用与刚性块体等体积的球形颗粒实时反演放出体空间形态。图9和图10分别为四组放矿数值试验所得高度50 m时的放出体形态以及放出体高度与最大半径拟合曲线。首先对比数值试验1和中粒径组物理试验所得放出体形态(图9(a)和图4(b))及其高度与最大半径之间的定量关系(图10中的黑色曲线和图5中的红色曲线),可以发现:同条件下的数值试验与物理试验结果基本一致,即证明了本次放矿数值模型及相应细观参数取值的可靠性。在此基础上,对比不同颗粒堆积体系下的四组放矿数值试验结果,由图10可知:四组数值试验所得放出体高度与其最大半径之间均满足式1所示的幂函数关系,拟合优度R2均大于0.996。当放出体高度较小时(如20 m),颗粒密实堆积体系下的数值试验2所得放出体宽度最大,颗粒自然堆积体系下的其余三组数值试验所得放出体宽度基本一致;而当放出体高度较大时(如50 m),数值试验2所得放出体宽度最小,数值试验4所得放出体宽度次之,数值试验1和3所得放出体宽度最大。然而有趣的是,由图9可知:颗粒自然堆积体系下的数值试验1、3和4所得放出体均呈倒置水滴形,其形态无显著差别;而颗粒密实堆积体系下的数值试验2所得放出体呈“下大上小”的近似正置水滴形。
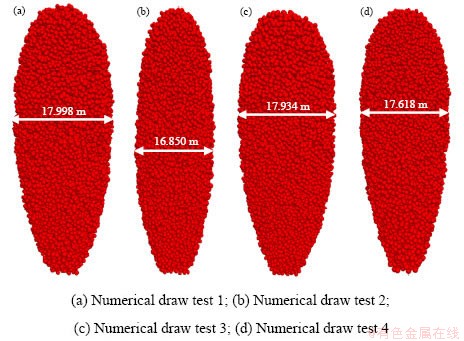
图9 四组放矿数值试验所得高度50 m时的放出体形态图
Fig. 9 The shapes of IEZs with the height of 50 m in four numerical draw tests
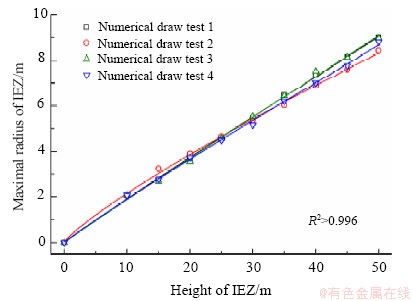
图10 四组放矿数值试验所得放出体高度与最大半径拟合曲线
Fig. 10 Fitting curves between the height and maximal radius of IEZ in four numerical draw tests
在利用图9定性分析的基础上,为定量分析不同堆积方式下放出体空间形态的差异性,并忽略放矿高度较小时放矿口对放出体形态的影响[7],故统计四组放矿数值试验所得30~50 m高度放出体的最大宽度所处高度(图11)。需要说明的是,图11中定义的“半高线”是指放出体1/2高度所在的高度水平线(如50 m高度放出体的“半高”为25 m),用以分析和表征放出体形态的纵向对称性。由图11可知:数值试验1、3和4所得放出体最大宽度所在高度均大于其相应半高线,即出现在整个放出体形态的上半部分——放出体形态呈“下小上大”的倒置水滴形;而数值试验2所得放出体最大宽度所在高度均小于其相应半高线,即出现在整个放出体形态的下半部分——放出体形态呈“下大上小”的近似正置水滴形。综上所述,在所研究的取值范围内,颗粒自然堆积体系下放矿所得放出体形态为倒置水滴形,而颗粒密实堆积体系下放矿所得放出体形态为正置水滴形。因此,针对放矿高度较大的大型自然崩落法矿山(如矿石层高度200~300 m),在相同放矿口间距条件下,若矿岩散体堆积体系过于密实,相邻的正置水滴形放出体更不易于相交,尤其是远离放矿口的区域,即矿岩散体密实堆积体系下放矿所得矿石贫损率会更大,或者说需要降低上述散体堆积条件下的采场结构参数。
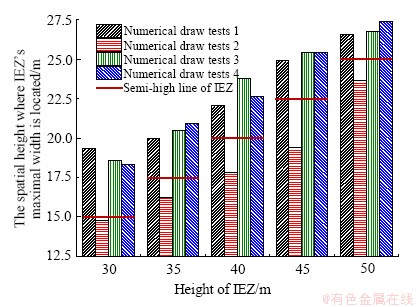
图11 四组放矿数值试验所得不同高度放出体的最大宽度所处高度
Fig. 11 The spatial height where the maximal width of IEZ of different height is located in four numerical draw tests
(2) 颗粒空隙率和配位数分析
为进一步探究不同颗粒堆积方式的差异性,故统计放矿前四组初始颗粒堆积体系中不同高度的空隙率、平均配位数及其概率分布(图12)。
由图12(a)分析可知:四组数值试验中初始颗粒堆积体系的空隙率均随高度的增大而增大,即重力作用下的颗粒堆积体系自上而下愈来愈密实;此外,数值试验1、3和4中颗粒自然堆积体系的空隙率及其变化规律基本一致,均明显大于数值试验2中颗粒密实堆积体系的空隙率。
由图12(b)分析可知:四组数值试验中初始堆积体系的颗粒平均配位数均随高度的增大而减小,即颗粒堆积体系的空隙率与平均配位数之间存在明显的负相关关系;此外,数值试验1、3和4中颗粒自然堆积体系的颗粒平均配位数及其变化规律差异不大,均明显小于数值试验2中颗粒密实堆积体系的颗粒平均配位数。
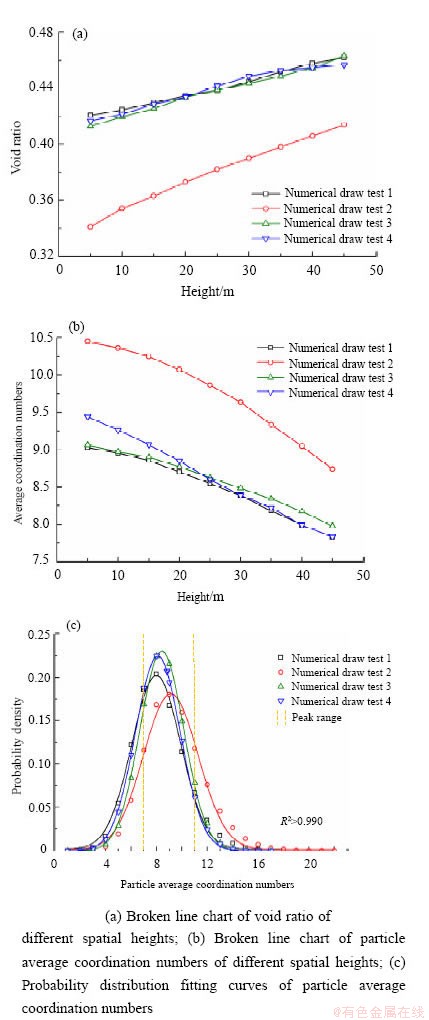
图12 四组初始颗粒堆积体系中不同高度的空隙率、平均配位数及其概率分布
Fig. 12 The void ratio, average coordination number and probability distribution of different heights in four initial particle packing systems
颗粒配位数的概率分布是描述颗粒堆积体系结构非均匀性的一个特征量[31]。由图12(c)分析可知:四组数值试验中颗粒平均配位数的概率分布均符合高斯分布,其拟合优度R2均大于0.99,峰值范围内的颗粒平均配位数区间约为[7,11];与其余三组试验相比,数值试验2中颗粒平均配位数的概率分布(红色拟合曲线)向右移动,对应于图12(b)中颗粒平均配位数的增加;此外,数值试验2中颗粒平均配位数概率分布(红色拟合曲线)的峰值范围更宽,即反映出颗粒密实堆积体系结构的各向异性程度更大,亦进一步表明:颗粒堆积体系结构的各向异性程度与放出体空间形态的差异性密切相关。
综上所述,在所研究的范围内(图7(a)、(c)、(d)),同一块度级配条件下,不同的颗粒不均匀块度空间分布形式对整个颗粒自然堆积体系的空隙率、平均配位数及其变化无显著影响,颗粒堆积体系的密实程度为影响崩落矿岩流动特性的关键因素。
(3) 矿岩块度、堆积高度和矿岩堆积体系的空隙率空间变化关系讨论
通过本文不同崩落矿岩空间分布状态下的四组放矿数值试验结果可以发现:在所研究的范围内,矿岩颗粒不均匀块度空间分布形式对其堆积体系中不同空间高度的空隙率变化无显著影响。众所周知,当其余各因素保持不变时,颗粒块度越大,其平均空隙率越大;颗粒所处空间位置越高(上覆矿岩高度越小),其平均空隙率越大。因此,针对图7(a)和(b)所示的两种矿岩颗粒空间分布形式,不同块度矿岩颗粒均匀混合(整个空间范围内的平均块度相同),矿岩颗粒空间高度为影响空隙率的主要因素,即矿岩颗粒堆积体系的空隙率均随空间高度的增大而增大。针对图7(c)所示的矿岩颗粒空间分布形式,在矿岩块度和所处空间位置这两因素的共同影响下,空间位置越低(上覆矿岩高度越大)的矿岩颗粒的平均空隙率越小。而有趣的是,针对图7(d)所示的矿岩颗粒空间分布形式,在矿岩块度和所处空间位置这两因素的相互作用下,依然是空间高度越小的矿岩颗粒的平均空隙率越小,即说明在本文所研究的取值范围内(矿岩块度范围为0.2~1.0 m,矿岩堆积体系高度为50 m),上覆矿岩高度为影响其堆积体积的空隙率空间变化的主要因素。而针对不同的矿岩块度和堆积高度取值范围,可以推测崩落矿岩堆积体系空隙率的空间变化规律可能不同。
相关研究表明:地下矿山开采过程中由爆破作用或自然崩落形成的矿岩散体是一种典型的宏观尺度颗粒物质体系[32, 33],具有“应力拱效应”和“粮仓效应”等显著特征[34, 35]。后续作者将利用统计物理学相关原理定量表征崩落矿岩的粒间力学行为,揭示矿岩块度、堆积高度和矿岩堆积体系结构特征之间的关联机制。
(4) 矿岩堆积体系结构与放出体形态关系讨论
通过本文放矿物理试验和数值试验结果可以发现:崩落矿岩堆积体系结构的不均匀性或各向异性和放出体形态变化规律之间存在显著相关性,并最终影响采场结构参数设计以及矿石贫损指标。相关研究表明:当颗粒间的空隙率达到某一临界值,该局部体系会形成一个具有力学稳定的刚性无序固体。对三维无摩擦的球形颗粒体系而言,该空隙率临界值为0.36;而对于有摩擦的非球形颗粒而言,该临界值将向更大的空隙率过渡[36]。因此,针对局部密实堆积的矿岩散体,在放矿过程中该局部体系内的散体间不再独立,可将其视为如图13所示的相互内锁而成的“颗粒团簇(Clusters)”。该局域结构的非均匀性将导致颗粒间动力学的非均匀性,进而影响崩落矿岩的流动特性。与此同时,若矿岩散体堆积体系过于密实,则容易出现“堵口”等不利于矿山正常生产作业的现象。
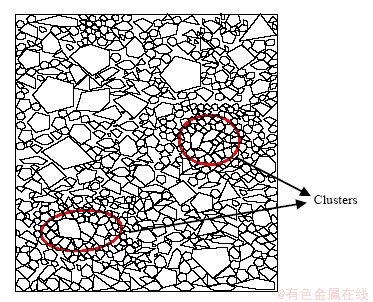
图13 局部密实堆积崩落矿岩示意图
Fig. 13 Schematic of local dense packing of caved ore and rock
后续作者将利用物理试验、数值试验和理论分析等手段,深入探究崩落矿岩间空隙率、配位数等构型状态量的临界值及其与颗粒形状、粒径等因素的关系,明确矿岩颗粒体系结构与动力非均匀性特征的对应关系,揭示崩落矿岩运移演化力学机理,进而形成基于矿岩颗粒体系结构特征的统一放出体形态表征模型。
3 结论
1) 在所研究的不同散体块度级配取值范围内,一定放矿高度条件下的散体平均粒径越大则放出体最大宽度越大。
2) 矿岩散体堆积体系的空隙率随高度的增大而增大,颗粒平均配位数均随高度的增大而减小。颗粒平均配位数的概率分布符合高斯分布,峰值范围内的颗粒平均配位数约为7~11。
3) 矿岩散体堆积体系结构的各向异性与放出体空间形态的差异性密切相关。随着散体堆积状态由自然堆积向密实堆积转变,散体堆积体系结构的各向异性程度变大,放矿所得放出体形态由倒置水滴形转变为正置水滴形,放出体最大宽度变小。因此,为降低矿石贫损率以及放矿口“堵孔”频率,实际崩落法矿山应尽量避免由爆破作用或散体长期堆积等原因造成的崩落矿岩极密实堆积状态。
REFERENCES
[1] EADIE B. A framework for modeling fragmentation in block caving[D]. Brisbane: The University of Queensland. Julius Kruttschnitt Mineral Research Centre, 2003: 1-5.
[2] PETERS D C. Physical modeling of the draw behavior of broken rock in caving[J]. Colorado School of Mines Quarterly, 1984, 79(1): 1-71.
[3] POWER G R. Modelling granular flow in caving mines: large scale physical modelling and full scale experiments[D]. Brisbane: The University of Queensland. Julius Kruttschnitt Mineral Research Centre, 2004: 45-73.
[4] CASTRO R, TRUEMAN R, HALIM A. A study of isolated draw zones in block caving mines by means of a large 3D physical model[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 860-870.
[5] 吴爱祥, 武力聪, 刘晓辉, 等. 无底柱分段崩落法结构参数研究[J]. 中南大学学报(自然科学版), 2012, 43(5): 1845-1850.
WU Ai-xiang, WU Li-cong, LIU Xiao-hui, et al. Study on structural parameters of sublevel caving[J]. Journal of Central South University (Science and Technology), 2012, 43(5): 1845-1850.
[6] 孙浩, 金爱兵, 高永涛, 等. 不同端壁倾角条件下放出体形态研究及最优崩矿步距的确定[J]. 工程科学学报, 2016, 38(2): 159-166.
SUN Hao, JIN Ai-bing, GAO Yong-tao, et al. Research of the isolated extraction zone form and determination of optimal independent advance under different end wall angles[J]. Chinese Journal of Engineering, 2016, 38(2): 159-166.
[7] SUN H, JIN A B, ELMO D, et al. A numerical based approach to calculate ore dilution rates using rolling resistance model and upside-down drop shape theory[J]. Rock Mechanics and Rock Engineering, 2020, 53(10): 4639-4652.
[8] 陈庆发, 王少平, 秦世康, 等. 柔性隔离层下多漏斗散体矿岩力链演化特征的离散元模拟[J]. 工程科学学报, 2020, 42(9): 1119-1129.
CHEN Qing-fa, WANG Shao-ping, QIN Shi-kang, et al. Discrete element simulation for evolution characteristics of multi-funnel mineral-rock force chain under flexible isolation layer[J]. Chinese Journal of Engineering, 2020, 42(9): 1119-1129.
[9] 朱晟, 钟春欣, 郑希镭, 等. 堆石体的填筑标准与级配优化研究[J]. 岩土工程学报, 2018, 40(1): 108-115.
ZHU Sheng, ZHONG Chun-xin, ZHENG Xi-lei, et al. Filling standards and gradation optimization of rockfill materials Chinese[J]. Journal of Geotechnical Engineering, 2018, 40(1): 108-115.
[10] 姚昕恺, 边疆, 王旭东. 等. 缩尺效应对铁路道砟力学特性影响的试验研究[J]. 岩土工程学报, 2018, 40(S2): 230-234+245.
YAO Xin-kai, BIAN Jiang, WANG Xu-dong, et al. Experimental study on influences of scale effect on mechanical properties of railway ballast[J]. Journal of Geotechnical Engineering, 2018, 40(S2): 230-234+245.
[11] 邢媛媛, 吴海波, 刘学建, 等. 颗粒级配对固相烧结碳化硅陶瓷的影响[J]. 无机材料学报, 2018, 33(11): 1167-1172.
XING Yuan-yuan, WU Hai-bo, LIU Xue-jian, et al. Grain composition on solid-state-sintered sic ceramics[J]. Journal of Inorganic Materials, 2018, 33(11): 1167-1172.
[12] 郑钢镖, 康天合, 柴肇云, 等. 运用Rosin-Rammler分布函数研究煤尘粒径分布规律[J]. 太原理工大学学报, 2006, 37(3): 317-319.
ZHENG Gang-biao, KANG Tian-he, CHAI Zhao-yun, et al. Applied the Rosin-Rammler distribution function to study on the law of coal dust particle-size distribution[J]. Journal of Taiyuan University of Technology, 2006, 37(3): 317-319.
[13] 祝杰, 刘振华, 杨云峰, 等. 运用Rosin-Rammler函数研究喷淋塔内液滴粒径分布规律[J]. 高校化学工程学报, 2015, 29(5): 1059-1064.
ZHU Jie, LIU Zhen-hua, YANG Yun-feng, et al. Applying the Rosin-Rammler function to study on drop size distribution in spray tower[J]. Journal of Chemical Engineering of Chinese Universities, 2015, 29(5): 1059-1064.
[14] 李昌宁, 龚晓南. 矿岩散体的非均匀度研究[J]. 矿冶工程, 2002(2): 37-39+44.
LI Chang-ning, GONG Xiao-nan. Study on the non-uniformity of loose body of ore rock[J]. Mining and Metallurgical Engineering, 2002(2): 37-39+44.
[15] 李响, 贾明涛, 王李管, 等. 基于蒙特卡罗随机模拟的矿岩崩落块度预测研究[J]. 岩土力学, 2009, 30(4): 1186-1190.
LI Xiang, JIA Ming-tao, WANG Li-guan, et al. Study of orefragment size prediction in block caving based on Monte Carlo stochastic simulation[J]. Rock and Soil Mechanics, 2009, 30(4): 1186-1190.
[16] CASTRO R, GOMEZ R, PIERCE M, et al. Experimental quantification of vertical stresses during gravity flow in block caving[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 127: 104237.
[17] 王洪江, 尹升华, 吴爱祥, 等. 崩落矿岩流动特性及影响因素实验研究[J]. 中国矿业大学学报, 2010, 39(5): 693-698+715.
WANG Hong-jiang, YIN Sheng-hua, WU Ai-xiang, et al. Experimental study of the factors affecting the ore flow mechanism during block caving[J]. Journal of China University of Mining and Technology, 2010, 39(5): 693-698+715.
[18] 张锦旺, 王家臣, 魏炜杰, 等. 块度级配对散体顶煤流动特性影响的试验研究[J]. 煤炭学报, 2019, 44(4): 985-994.
ZHANG Jin-wang, WANG Jia-chen, WEI Wei-jie, et al. Experimental investigation on the effect of size distribution on the flow characteristics of loose top coal[J]. Journal of China Coal Society, 2019, 44(4): 985-994.
[19] 任凤玉, 刘洋, 何荣兴, 等. 放矿条件下塌陷区内尾砂穿流特性[J]. 东北大学学报 (自然科学版), 2020, 41(6): 858-862+887.
REN Feng-yu, LIU Yang, HE Rong-xing, et al. Flow-through features of tailings in subsidence area under ore drawing conditions[J]. Journal of Northeastern University (Natural Science), 2020, 41(6): 858-862+887.
[20] 李涛. 崩落法放矿过程中散体矿岩运移规律研究[D]. 北京: 北京科技大学土木与资源工程学院, 2018: 77-85.
LI Tao. Study on the migration law of granular ore rock under draw by caving method[D]. Beijing: University of Science and Technology Beijing. School of Civil and Resource Engineering, 2018: 77-85.
[21] 柳小波, 王连成. 非均匀崩落矿岩散体流动的仿真模型[J]. 东北大学学报(自然科学版), 2017, 38(8): 1167-1172.
LIU Xiao-bo, WANG Lian-cheng. Simulation model of granular flow of the non-uniform caved ore and rock[J]. Journal of Northeastern University (Natural Science), 2017, 38(8): 1167-1172.
[22] SUN H, GAO Y T, ELMO D, et al. A study of gravity flow based on the upside-down drop shape theory and considering rock shape and breakage[J]. Rock Mechanics and Rock Engineering, 2019, 52(3): 881-893.
[23] 陶干强, 杨仕教, 任凤玉. 崩落矿岩散粒体流动性能试验研究[J]. 岩土力学, 2009, 30(10): 2950-2954.
TAO Gan-qiang, YANG Shi-jiao, REN Feng-yu, et al. Experimental research on granular flow characters of caved ore and rock[J]. Rock and Soil Mechanics, 2009, 30(10): 2950-2954.
[24] 金爱兵, 陈帅军, 孙浩, 等. 基于不均匀粒径分布的颗粒穿流特性[J]. 中南大学学报(自然科学版), 2020, 51(6): 1673-1681.
JIN Ai-bing, CHEN Shuai-jun, SUN Hao, et al. Characteristics of particle percolation based on inhomogeneous particle size distribution[J]. Journal of Central South University (Science and Technology), 2020, 51(6): 1673-1681.
[25] JIN A B, SUN H, WU S C, et al. Confirmation of the upside-down drop shape theory in gravity flow and development of a new empirical equation to calculate the shape[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 92: 91-98.
[26] CASTRO R. Study of the mechanisms of gravity flow for block caving[D]. Brisbane: University of Queensland. Julius Kruttschnitt Mineral Research Centre, 2006: 65-93.
[27] PIERCE M E. A model for gravity flow of fragmented rock in block caving mines[D]. Brisbane: University of Queensland. Julius Kruttschnitt Mineral Research Centre, 2009: 45-90.
[28] ELMO D, ROGERS S, DORADOR L, et al. An FEM-DEM numerical approach to simulate secondary fragmentation[C]//Computer Methods and Recent Advances in Geomechanics: Proceedings of the 14th International Conference of International Association for Computer Methods and Recent Advances in Geomechanics, 2014 (IACMAG 2014). Taylor & Francis Books Ltd, 2015: 1623-1628.
[29] 孙浩, 陈帅军, 高艳华, 等. 基于刚性块体模型的近-远场崩落矿岩流动特性[J].工程科学学报, 2021, 43(02): 205-214.
SUN Hao, CHEN Shuai-jun, GAO Yan-hua, et al. Research on near/far-field flow characteristics of caved ore and rock based on rigid block model[J]. Chinese Journal of Engineering, 2021, 43(02): 205-214.
[30] Itasca Consulting Group Inc. PFC 6.0 documentation [EB/OL]. [2020-07-11]. http://docs.itascacg.com/pfc600/pfc/docproject/index.html.
[31] 赵仕威. 颗粒材料物理力学特性的离散元研究[D]. 广州: 华南理工大学土木与交通学院, 2018: 58-64.
ZHAO Shi-wei. Discrete Element Investigation of Physical and Mechanical Properties of Granular Materials[D]. Guangzhou: South China University of Technology. School of Civil Engineering and Transportation, 2018: 58-64.
[32] KOU B Q, CAO Y X, LI J D, et al. Granular materials flow like complex fluids[J]. Nature, 2017, 551(7680): 360-363.
[33] 孙其诚, 刘晓星, 张国华, 等. 密集颗粒物质的介观结构[J]. 力学进展, 2017, 47: 263-308.
SUN Qi-cheng, LIU Xiao-xing, ZHANG Guo-hua, et al. The mesoscopic structures of dense granular materials[J]. Advances in Mechanics, 2017, 47: 263-308.
[34] 陆坤权, 刘寄星. 颗粒物质(上)[J]. 物理, 2004, 33(9): 629-635.
LU Kun-quan, LIU Ji-xing. Static and dynamic properties of granular matter (I) [J]. Physics, 2004, 33(9): 629-635.
[35] 陆坤权, 刘寄星. 颗粒物质(下)[J]. 物理, 2004, 33(10): 713-721.
LU Kun-quan, LIU Ji-xing. Static and dynamic properties of granular matter (II) [J]. Physics, 2004, 33(10): 713-721.
[36] BI D, ZHANG J, CHAKRABORTY B, et al. Jamming by shear[J]. Nature, 2011, 480(7377): 355-358.
Research on flow characteristics of caved ore and rock based on inhomogeneous particle size distribution
SUN Hao1, 2, ZHU Dong-feng1, 2, JIN Ai-bing1, 2, YIN Ze-song1, 2
(1. Key Laboratory of Ministry of Education for Efficient Mining and Safety of Metal Mine, University of Science and Technology Beijing, Beijing 100083, China;
2. School of Civil and Resources Engineering, University of Science and Technology Beijing, Beijing 100083, China)
Abstract: To reveal the migration and evolution mechanism of caved ore and rock under the condition of inhomogeneous particle size distribution, a series of physical and numerical draw experiments were carried out to study the flow characteristics of caved ore and rock. The flow characteristics of caved ore and rock were quantitatively studied under different particle size distributions and particle packing systems from the aspects of the IEZ’s shape change law, void ratio, the average coordination number and its probability distribution of caved ore and rock. The main research results prove that: 1) In the range of different particle size distribution values studied, the larger the average particle size is, the larger the IEZ’s maximal width is. 2) The void ratio of packing system of caved ore and rock increases with the increase of spatial height, while the average coordination number of particles decreases with the increase of spatial height. The probability distribution of the particle average coordination number conforms to the Gaussian distribution, and the average coordination number of particles in the peak range is about 7~11. 3) With the change of packing state from natural packing to dense packing, the anisotropy degree of the packing system of caved ore and rock becomes greater, the IEZ’s shape changes from the upside down drop shape to the normal drop shape, and the IEZ’s maximal width is smaller, which can provide a strong support for the establishment of a unified IEZ characterization model based on the structural characteristics of particle system of caved ore and rock.
Key words: draw; inhomogeneous particle size; packing pattern; caved ore and rock; flow characteristics; rigid block model
Foundation item: Project (52004017, 51804018) supported by the National Natural Science Foundation of China; Project (2020M670138) supported by the China Postdoctoral Science Foundation; Project (FRF-TP-19-026A1, FRF-IDRY-20-021) supported by the Fundamental Research Funds for the Central Universities
Received date: 20 - - ; Accepted date: 20 - -
Corresponding author: JIN Ai-bing; Tel: +86-13910064563; E-mail: jinaibing@ustb.edu.cn
(编辑 某某某)
基金项目:国家自然科学基金资助项目(52004017,51804018);中国博士后科学基金项目(2020M670138);中央高校基本科研业务费专项资金资助项目(FRF-TP-19-026A1,FRF-IDRY-20-021).
收稿日期:20 - - ;修订日期:20 - -
通信作者:金爱兵,教授,博士;电话:13910064563;E-mail:jinaibing@ustb.edu.cn