J. Cent. South Univ. (2017) 24: 2058-2070

DOI: https://doi.org/10.1007/s11771-017-3615-5

A nonlinear hydroelastic method considering wave memory effect for ship load responses in irregular waves

CHEN Zhan-yang(陈占阳)

Department of Naval Architecture and Ocean Engineering, Harbin Institute of Technology at Weihai,Weihai 264209, China

Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract: Since the amplitude and frequency of irregular waves change with time, great difficulties are brought for solving ship load responses in random waves. To take the effect of various frequencies of irregular waves into consideration in load responses of hull, the wave memory effect is necessary. A semi-analytical method is introduced for the time-domain retardation functions, and then a nonlinear hydroelastic method considering memory effect for ships in irregular waves is proposed. Segmented self-propelling model experiments of a container ship were carried out in a towing tank, a ship motion measuring device for self-propelling model test was designed. Whipping responses of the ship in regular and irregular waves are analyzed. Finally, the calculation results are compared with those measured by segmented model experiments, and the result indicates that the memory effect has little effect on load responses of ship in regular waves, but pronounced effect on results in irregular waves. Moreover, the presented method is reasonable for the prediction of ship load responses in irregular waves.

Key words: hydroelasticity; memory effect; retardation function; segmented self-propelling model test; irregular waves

1 Introduction

It is a fact that hydroelastic method, which considers the interaction between ship elastic deformation and forces around flow field, fully utilizes the flow field information around the floating body to predict the motion of rigid body, elastic deformation, shear and bending moment of floating body structure. It has a broader development prospect for dealing with strength check, fatigue life calculation and structural dynamic response analysis for post processing of floating structure. Currently there are a large number of researches who spare much effort on the investigation of hydroelastic theory in both home and abroad [1-7].

However, these researchers mainly focus on hydroelastic method that calculates ship motion and load responses in regular waves. Lloyd’s Register [8] pointed out the determination of design load of warships should be determined on statistical distribution of load responses in irregular waves because the actual waves which hulls encountered are nonlinear random waves. Especially for high sea states, therefore, it is of great importance to propose a nonlinear time-domain prediction method for load responses of hull in irregular waves.

Compared with regular waves, irregular waves have two characteristics, i.e. various amplitudes and frequencies. The existing hydroelastic method in irregular waves is mostly based on solving forces and hydrodynamic coefficients through the characteristic frequency or main frequency in the energy spectrum [9]. However, the “characteristic frequency method” cannot consider the effect of various frequency components on load responses. Besides, because of the random behavior of actual waves, the hull motion amplitude, frequency and other physical quantity vary all the time, which brings great difficulties for the solving of hull response in irregular waves.

In order to fully take the effect of sub-wave frequency into consideration, the retardation function is considered for memory effect [10]. Due to the limitation of numerical method, the commonly method is based on the truncated frequency, and the truncated error is ignored. However, XIAO et al [11] pointed out that the characteristics of damping coefficient should be known in order to achieve necessary accuracy, which proves the influence of truncated error should not be ignored. In the previous publications, most of the researchers solved the hydrodynamic coefficients at high frequency based on numerical quadrature methods [12] or Fast Fourier Transfer method (FFT) [13]. As a matter of fact, integration within the whole frequency range needs to be solved in these methods, the high computational cost (hydrodynamic coefficients in all the frequency) cannot be avoided. Therefore, there is a real need to develop a convenient and accurate method for the calculation of time-domain retardation function.

Segmented ship model experimental analysis can be considered as a first approach for studying the load responses of elastic ship [14]. However, owing to the difficulties of this technique, segmented ship model tests for the hydroelasticity of ships in the published papers are mostly towing test [15, 16]. Those models cannot reflect mechanical properties of ships sailing in actual sea conditions, especially for whipping phenomena in high sea states. According to Ref. [17], towing test method increases the high frequency load responses artificially, which usually shows incorrect results. Therefore, segmented self-propelling model experiment should be adopted to solve this problem.

The present work mainly focuses on prediction of ship load responses and experimental verification in irregular waves. In Section 2, a three-dimensional (3-D) nonlinear time-domain hydroelastic numerical model considering the memory effect is proposed. In order to consider the effect of various wave frequencies on load responses in irregular waves, a semi-analytical method is introduced for the time-domain retardation functions and added mass. The wave excitation force and slamming force are calculated by time-domain convolution theory as well as the momentum slamming theory. In Section 3, tests are carried out using a segmented self-propelling ship model of a 13000-TEU container ship in the towing tank. A ship motion measuring device for self-propelling model test is designed. The effects of wave memory effect on ship load responses in regular and irregular waves are studied in Section 4. Numerical calculations and comparison results indicate that the computational results presented in this work are more accurate for prediction of ship load responses in irregular waves. Finally, conclusions are presented in Section 5.

2 Computational methods

2.1 Hydroelastic motion equation considering memory effect

In this work, two nonlinear factors are considered: instantaneous wetted surface of hull and slamming forces. The hydroelastic motion equation considering the memory effect in the time domain is expressed as follows:

        (1)

where a, b and c denote generalized structural mass matrix, generalized structural damping coefficient matrix and generalized structural stiffness matrix, respectively; μ denotes the added mass, which is a r×r constant matrix; K(τ) denotes retardation function, which is also a r×r matrix dependent on time τ, which depends on the shape of the underwater portion of hull and time interval and reflects characteristic of wave damping and hydrodynamics; F_I(t) is incident wave force; F_D(t) is diffraction wave force; F_slam(t) is slamming force.

2.2 Calculation of nonlinear fluid forces

For the calculation of the wave exciting force in regular waves, the original method is the integration on the average wetted surface. In this work, with the help of the interception of instantaneous grid, the incident wave force and diffraction wave force can be written as

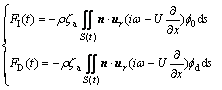
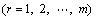                       (2)

where f₀ and f_d are instantaneous incident potential and diffraction potential under unit wave amplitude, respectively; ζ_a is wave amplitude; n is the normal vector, which is defined positive when pointing into body from the boundary surface; u_r is the rth principal modes of the structure.

The irregular waves can be regarded as a superposition of a finite number of regular waves, if the forces of hull are solved based on the single frequency, the characteristic of load responses in irregular waves cannot be reflected accurately. TIAN [9] used the linear superposition method to solve the problem. However, this requires a large number of computation cost. In addition, the numerical quadrature is still very likely to give unreliable and inaccurate results because of the nature of the methods. To solve this problem, the time-domain convolution theory is used to calculate incident wave force of flexible hull in irregular waves.

The convolution relationship between time-domain wave forces and frequency-domain wave forces are presented by CUMMINS [18], which is improved to hydroelastic theory. Then the incident wave force and diffraction wave force in irregular waves can be expressed as

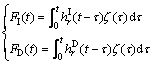
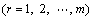      (3)

where ζ(τ) is wave elevation of irregular waves; 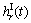and are the impulsive response functions of incident wave force and diffraction wave force respectively:

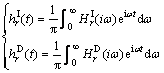(r=1, 2, …, m)     (4)

where 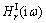and are the frequency response functions induced by the harmonic incident wave force and diffraction wave force with unit amplitude respectively and can be calculated by the frequency-domain hydrostatic theory. Thus the contribution from the whole wave frequency range in irregular waves to wave excitation force can be considered.

The hydrostatic restoring forces have been directly computed through the composition method including the integration of hydrostatic pressure from instantaneous hull wet surface S (t) and hull gravity in this work.

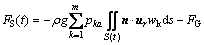(r=1, 2, …, m)(5)

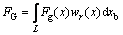                         (6)

where w_k is the kth mode vertical displacement; F_g(x) is weight collection degree of each station.

Unlike linear hydroelastic theory, the nonlinear hydroelastic method takes into account the slamming forces in this work. The momentum slamming theory is used to predict slamming loads:

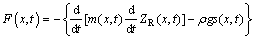     (7)

where m(x, t) is the instantaneous added mass; Z_R(x, t) is vertical relative ship motion to wave; s(x, t) is instantaneous sinking area.

The discrepancy that whether the memory effect should be considered embodies in the radiation force. If memory effect is not considered, the radiation force of the hull can be expressed as

               (8)

where ω is the wave frequency; coefficient A(ω) is in phase with the acceleration and acts as an additional mass in the equation of motion; coefficient B(ω) is in phase with the velocity and appear as an additional damping. Both of them are r×r matrices.

If memory effect of wave is considered, the radiation force of the hull can be expressed as

           (9)

In the rigid theory, x_r(t) is the motion vector of the hull, r=1, 2, …, 6, denotes 6 degree of freedom motions; In the hydroelastic theory, x_r(t) is the rth mode principal coordinates, r=1, 2, …, m.

Then the process of solution of μ and K(τ) is introduced in detail.

2.3 Calculation of infinite frequency added mass μ and retardation function K(τ)

For a steady harmonic motion of the flexible hull with frequency ω, we can express the motion as

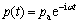                              (10)

where p(t) is the mode principal coordinates.

Substituting Eq.(10) into Eq. (8), we have:

          (11)

Expressing F_R(t) in the following form, we have:

              (12)

Equating the right-hand-side of Eq. (11) and that of Eq. (12), we have the relations between time domain and frequency domain:

               (13)

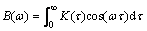                    (14)

As seen from Eq.(14), B(ω) and K(τ) are a Fourier transfer pair. Therefore, K(τ) can be expressed in terms of B(ω) as

                   (15)

Equations (13) and (15) are one of forms of the Kramer-Kronig relations relating A(ω) and B(ω). From Eq. (13), it is easy to see that μ=A(∞) and therefore μ is also referred as infinite frequency added mass.

Through the above derivation, the retardation function has the following characteristics:

1) B(ω) should vanish at ω= 0 and ω→∞ ;

2) K(τ) should vanish as τ→∞ .

3) 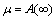as not dependent on ω.

Obviously, the accuracy of the load responses depends on the data quality. However, in real practice, due to limitation of the computer resources, the numbers of the frequency range and wave frequencies are finite. A key difficulty is how to estimate the behavior of the damping coefficient at high frequency. To avoid the numerical difficulties and high computational cost, a semi-analytical method is presented in this work for accurate evaluation of Eq. (15) then.

For the integral of Eq. (15), a truncated frequency is firstly chosen to divide the whole frequency range (0, ∞) into 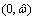and Then Eq. (15) can be expressed as

(16)

Observation has shown that B(ω) slowly varies over the whole range. For the highly oscillatory function 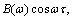it would be easier to numerically approximate the slow varying function B(ω). Here the domain 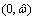is divided into finite sub-domains 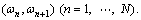Unlike the numerical quadrature which approximates the whole integrand with a polynomial, the presented method approximates B(ω) with a linear function in

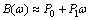                             (17)

where ;.

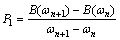The contribution to K(τ) from the domain 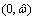can be expressed as

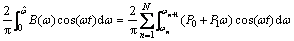
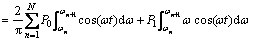
where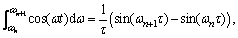

The contribution from range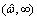 to retardation function will then be analyzed. Since the fluid damping coefficient would vanish asB(ω) is approximated with an exponentially decay function in this range:

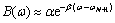                         (18)

where α and β are undetermined coefficients, in order for B(ω) to vanish as β should be larger than 0.

α and β are determined so that B(ω) and its first derivative are continuous at It is not hard to show that

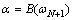;           (19)

The first derivative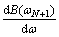can be approximated using finite differencing. In order to keep the results reliable and accurate, this is divided into two cases:

1) When B(ω)>0, Eq. (18) is then 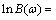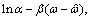α and β can be determined from the known variation of damping coefficient versus frequency by least square method;

2) When B(ω)<0, α and β can be obtained by average of derivative.

The contribution from range 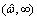is then,

           (20)

Substituting Eqs. (17) and (20) into Eq.(16), the retardation function matrix K_rk(τ) can be obtained. Thus,the integral of time-domain retardation function will be solved [19].

Based on the principles above, the time-domain retardation function is predicted, as shown in Fig. 1, which indicates that this method can give reliable and accurate results and the time retardation function obtained by this method is feasible.

It has been found in the actual calculation process that the determination of the truncated frequency depends on the specific circumstances, which is between 1.0 and 2.0 rad/s. Time-domain retardation function of hull has the character of fast decay, which is determined by its physical characteristics. Besides, we can see that from Fig. 1 the decay period of flexible mode is shorter than that of rigid mode and the decay period of high order mode is shorter than that of low order mode. For general vessels, K(τ) can be considered as zero when time is between 50 and 100 s, by which the computation time has been saved when the numerical calculation of convolution integration has been conducted in time domain motion equations.

2.4 Verification of calculation efficiency of time- domain retardation function

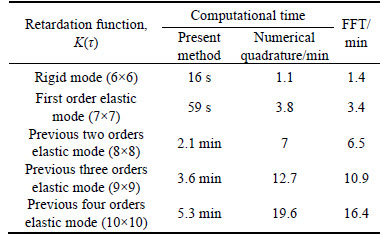
To confirm the high efficiency of the present method for time-domain retardation function, the computational time of the present method and the numerical quadrature methods, as well as FFT method of different cases are summarized in Table 1. In this work, the computations are made on an 8 CPU workstation with 3.4 GHz, on windows Win7 system.

As seen from Table 1, the high efficiency of the present method of time-domain retardation function is demonstrated. In each case, it is evident that the computational time of the present method is much less than that of the conventional methods, especially the more the number of elastic mode considered is, the more obvious the advantages of the present method are.

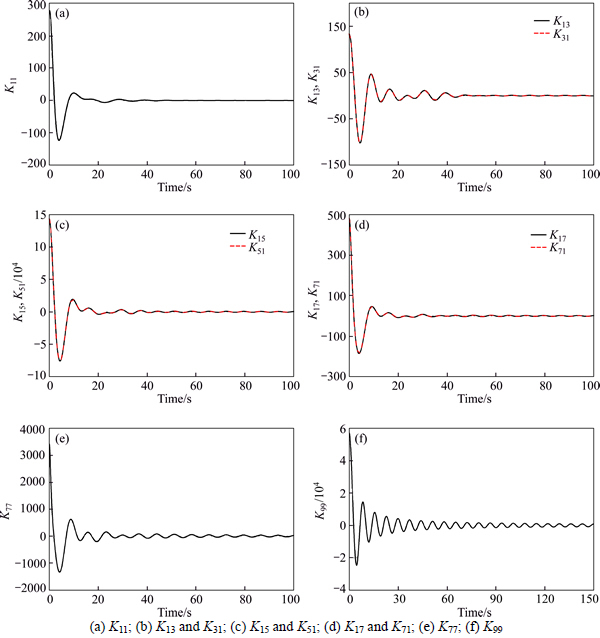
Fig. 1 Time histories of retardation function:

Table 1 Computational time of different methods

2.5 Solution of nonlinear equation

For the solution of the second-order differential motion Eq. (1), the fourth-order Runge-Kutta method has been adopted in this work, which is explicitly single step with 4th-order accuracy. Due to the retardation function 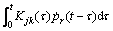is obtained, unlike conventional hydroelastic motion equations, the value of half step has been computed in the process of Runge-Kutta solution.

Since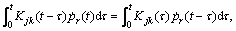 the convolution integral problem is solved by the second order differential equation, the equation is expressed as

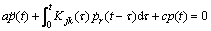           (21)

Since 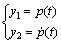is written in the form of the standard first order differential equation as

    (22)

The initial conditions can then be simplified as follows:

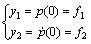                             (23)

Since 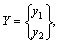△t is the time step, n is step number, then

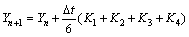              (24)

When n=0, K₁ and K₂ are written in the following forms:

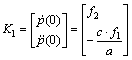                      (25)

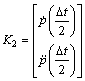
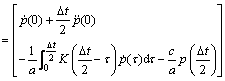     (26)

where 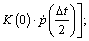and

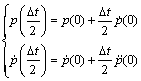                     (27)

K₃ is written in the following forms:

     (28)

where 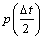and are different from Eq.(28):

                   (29)

and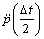in the right side items of equation can be obtained by Eq. (27) as

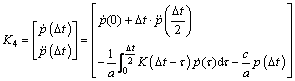(30)

where

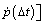
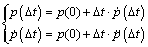                    (31)

and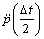in the right side items of equation can be obtained by Eq. (29). So p(Δt) and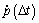are obtained, then t=2Δt, t=3Δt, …, t=nΔt. p(Δt) and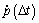in each time can be obtained.

Then based on modal superposition principle, the time-domain displacement w(x,t), bending moment M(x, t) and shearing force V(x, t) of each cross section of ship can be obtained.

                     (32)

where w_r(x), M_r(x) and V_r(x) are the r-th principal mode of displacement, bending moment and shearing force of hull beam respectively. r=1, 2, …, 6 denotes motion modes of rigid hull; r≥7 denotes motion modes of flexible hull.

3 Segmented self-propelling model test

3.1 Model design

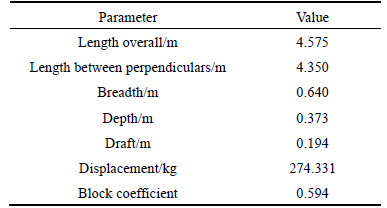
In order to verify the accuracy of the proposed numerical method, a segmented ship model self- propelling test of a 13000-TEU container ship was carried out in the towing tank of Harbin Engineering University, China, which has dimensions of 108 m×7 m×3.5 m. Waves are made by a rocker flap wave generator. The load responses and vibration phenomena acting on the ship girder induced by slamming in regular and irregular waves are studied. The model scale is 1:80, and the model test cases are performed under head sea conditions. Model characteristics are presented in Table 2.

Table 2 Main parameters of model

The fiberglass-reinforced plastics model has 20 divisions and is cut into 7 segments by using the 2nd, 4th, 6th, 8th, 10th and 12th divisions (see Fig. 2). The segmented hulls are connected together by the longitudinal rectangular steel backbones and made watertight by rubber membranes (see Fig. 3). The vertical bending stress at sections A-F, which can be used to obtain bending moments based on the calibration results of backbones before test, is measured by four rosette strain gauges placed on the backbones.

The propulsion system, which was controlled to maintain the forward speed and heading angle when the motion was disturbed by waves, is arranged at the stern of model. Figure 4 shows the ship model launching. Before the wave load test, by a hammering test of the ship model in wet mode, the first and second order natural frequencies were measured to be 0.95 and 2.085 Hz, respectively.

3.2 Self-propelling model motion measuring device

In order to obtain load and motion responses of the model during measurements, a measuring system is assembled. The flowchart of the measuring system and points are presented in Fig. 5. The wave-height gauge for the wave height was located at the bow of the model. Two video cameras were used to record the test procedures. The pressure sensors and accelerometer were located on the model shell to measure the slamming pressure and vertical acceleration. This work mainly focuses on experimental verification of the presented method, so the vertical bending moments are principal research contents.

In towing test, the motion signals of ship model are usually measured by seaworthiness instruments, which will restrict the freedom of motion of the model in some way. In order to reproduce the motion characteristics of ship in waves, self-propelling ship model test is necessary. Compared with the previous towing test [20], the yaw problem of the self-propelling ship model needs to be solved firstly. Therefore, a self-propelling model motion measuring device, as shown in Fig 6, was designed.

This device was fixed with screws on the center line of the model. The device has two measuring rods that limit the yaw motion of ship model to make it sail as expected. During the test, the heave H₁ and H₂ of the two measuring rods are obtained by the sensors mounted on the measuring device. The distances L₁ and L₂ from the two measuring rods to the gravity center of ship model are known. In order to obtain the heave and pitch of the position at the model’s gravity center, the interpolation function for heave H₀ and pitch θ₀ can be expressed as

                          (33)

                         (34)

Furthermore, the device can not only obtain the motion of any position of the model, but also obtain the relative displacement between the bow and waves. And then the vertical relative speed between the bow and waves can be obtained, which provides beneficial reference data for the prediction of slamming pressure.

This measuring device is suitable for many kinds of hydrodynamic experiments, e.g., calm water resistance, propulsion, seakeeping performance, and wave load tests.

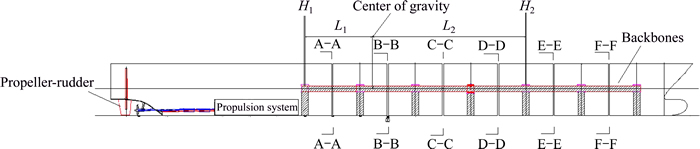
Fig. 2 Ship model equipment

Fig. 3 Longitudinal rectangular steel backbones system

Fig. 4 Ship model launching

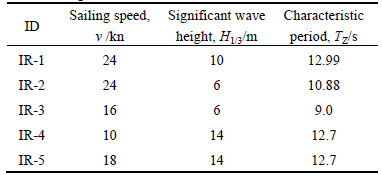
Tables 3 and 4 present case IDs and wave conditions. In this work, the ISSC double parameters wave spectrum is used for the generation of irregular waves. The ISSC spectrum was presented at the 12th International Towing Tank Conference (ITTC) in 1969.Now it has been a widely used wave spectrum for naval architects.

3.3 Analysis of experiment results

3.3.1 Measured data in regular waves

The experiment results in different sea states show that there exist high frequency components in the total vertical bending moments (VBM). In Fig. 7, the heavy and pitch responses measured by the self-propelling measuring device are shown. VBM amidships in extreme sea states in regular waves are decomposed into high frequency (HF) slamming moments and low frequency (LF) wave moments by filter theory.

Hull vibration caused by waves is divided into two types: one is whipping that belongs to a transient vibration caused by slamming. Whipping phenomenon often happens in moderate and high sea states. The other is springing, which is a kind of steady forced vibration when the encounter frequency is equal to the natural frequency of the ship itself.

Then we study the whipping responses by investigating the excitation which corresponds to the modal force of two-node vertical bending because of the slamming load. Figure 7 clearly shows that time histories of HF slamming moments are free damping. It is shown that the ship girder generates transient vibration induced by slamming loads. This is quite different from the steady time histories of springing responses. It is well-known that the slamming is a transient response,once the ship subjects to the excitation force, the ship girder oscillation amplitude is the maximum, then the amplitudes of whipping moments decay because of structural and hydrodynamic damping until next slamming occurs. Moreover, with the increasing wave height, slamming becomes more serious and whipping responses become much larger.

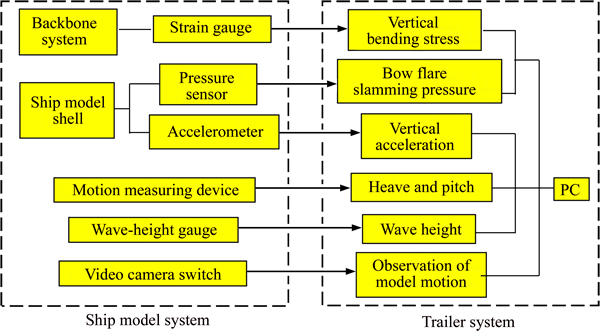
Fig. 5 Flowchart of measuring system and points

Fig. 6 Self-propelling measuring device:

Table 3 Regular wave case IDs and wave conditions

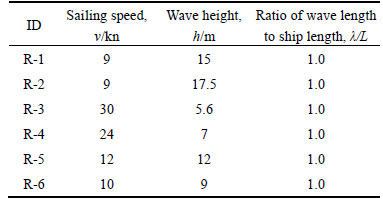
Table 4 Irregular wave case IDs and wave conditions

In order to emphasize the proportion of HF bending moments in the total bending moments in different sea states，the proportion of the HF bending moments and LF bending moments at various wave heights are compared, as shown in Fig. 8.

From the comparison, it can be concluded that as the wave height increases, the proportion of LF wave moments begins to decrease. The proportion of HF slamming load, unlike the LF load, increased dramatically. When wave height increases from 5 m to 17.5 m, it clearly shows that proportion of HF slamming moments increases from 9.99% to 62.38% because of severe whipping.

3.3.2 Measured data in irregular waves

For the test in irregular waves, Fig. 9 shows time histories of motion and load responses in irregular waves.

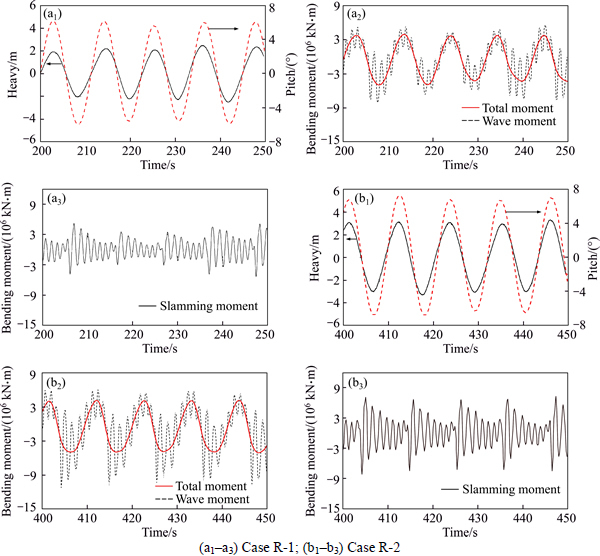
Fig. 7 Time histories of motion and load responses:

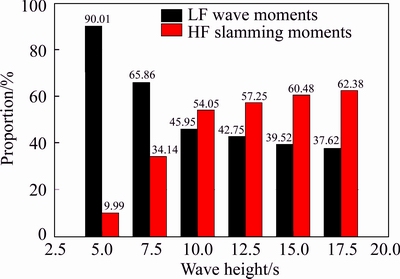
Fig. 8 Proportion of HF and LF load components at various wave heights (v=9 kn)

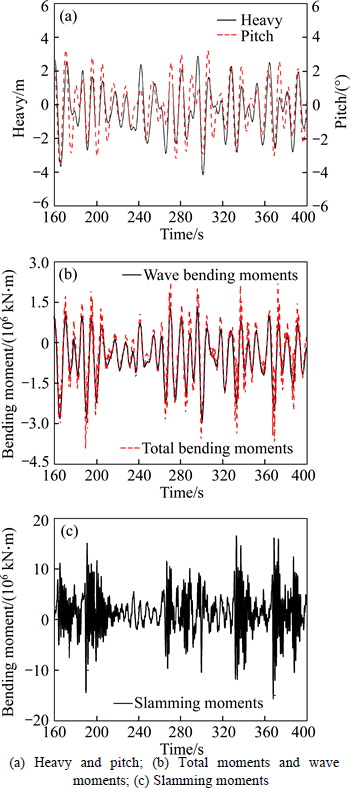
Fig. 9 Time histories of motion and load responses in Case IR-1:

From Fig. 9, non-negligible slamming and whipping are also observed in irregular waves, which is the same as the regular waves. Moreover, the slamming phenomenon can be obviously observed from the video. As a consequence, in order to improve the computational results, the severe nonlinear phenomena must be considered in prediction of load responses in irregular waves.

4 Results and discussion

4.1 Effect of wave memory effect on results in regular waves

In order to verify the method and program presented in this work, the load responses of the container ship measured are predicted.

Before the calculation of hydrodynamics, based on the method of 3-D grid auto-generation of flexible hull wet surface, combining with the finite element mode analysis method, the hydrodynamics grid of the container ship is generated. Figure 10 shows 3-D panel mesh model of rigid hull and flexible hull, which reflects the 3-D shape of hull accurately, and improves computational efficiency of 3-D hydroelastic method.

The purpose of memory effect is considering influence of various wave frequencies on the results. The frequency of the regular waves is mono-frequency, and then the influence of memory effect on results in regular waves is studied as follows:

Firstly, assuming that the motion is periodic, let the body move periodically in the r-th mode as

                  (35)

Secondly, in view of the fact that K(t) is independent on velocity of hull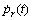and acceleration 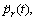Assumeso L(0)=0; 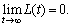As time goes to infinity and steady state is reached, substituting Eq. (35) into Eq. (9), we have

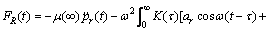
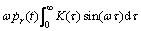              (36)

Since A(ω), B(ω) and K(τ) (or L(t)) are a Fourier transfer pair respectively, then

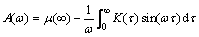
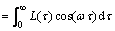                    (37)

Fig. 10 3-D panel mesh model:

                   (38)

Substituting Eqs. (37) and (38) into Eq. (36), we have,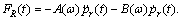

Then in order to investigate the influence of memory effect on load responses of hull in regular waves, the traditional method without memory effect and the proposed method with memory effect are applied to predict VBM amidships, and the calculation results are compared with experimental results (Exp), as shown in Fig. 11.

As seen from Fig. 11, very good agreement between the calculation and experimental results is observed. For the ship responses in regular waves, it is evident that the calculation results considering memory effect are in good agreement with that from the traditional method, which confirms theoretical derivation above. Besides, the numerical method presented in this work is proved to predict load responses of hull accurately. Then the proposed method is improved in irregular waves.

4.2 Numerical results of irregular waves

In order to demonstrate whether the method developed in this thesis is applicable for this research, the VBM amidships in irregular waves are studied, the experimental results are compared with that calculated by characteristic frequency method (without memory effect) and the method presented in this work (with memory effect), as shown in Fig. 12.

As seen from Fig. 12, the calculation results from the numerical method presented in this work shows good agreement with the experimental results when memory effect is considered in irregular waves. Besides, there is a remarkable difference in the response characteristics between the presented method and traditional method. For “characteristic frequency method”, the force and hydrodynamic coefficient are obtained by a single frequency, which cannot reflect characteristic of load responses in irregular waves, the calculation results with memory effect are in better agreement with experimental results.

In addition，for the high sea states，such as Figs. 12(c) and (d), nonlinear characteristics of HF responses of experimental results are more significant than those of calculation results. This is because the waves which the model encounters are real waves. In this condition, the model motion and load responses are of full nonlinear effects. The mathematical model only considers the instantaneous wetted surface and slamming forces. Other nonlinear factors, such as free-surface nonlinearity, are not considered, which is the author’s future work.

5 Conclusions

1) The proposed semi-analytical method for retardation function does not suffer the numerical difficulties of the numerical quadrature, which significantly reduces the number of the frequencies needed to compute A(ω) and B(ω), thus reducing the computational cost. The efficiency of the present numerical approach is also testified which indicates that the proposed numerical scheme is time-saving.

Fig. 11 Comparison of VBM amidships in regular waves:

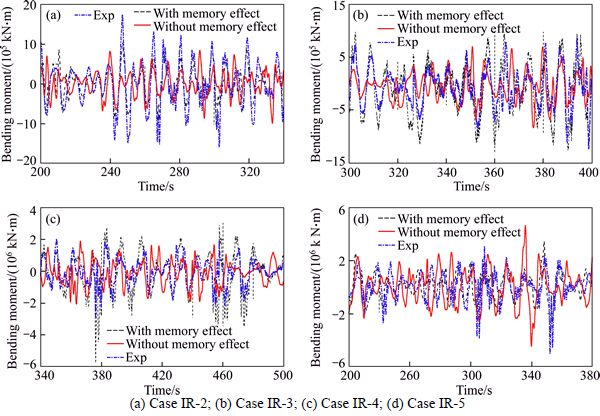
Fig. 12 Comparison of VBM amidships in regular waves:

2) In order to measure the model motion and solve the yaw problem, a model motion measuring device for self-propelling test is designed. The measuring results in regular and irregular waves are analyzed. The presented technical details of this device are feasible.

3) For load responses in regular waves, the memory effect can be ignored; however, the memory effect has great effect on load responses of hull in irregular waves. In addition, the results considering memory effect are in good agreement with the test data, which proves that the method presented is suitable for predicting the load responses in irregular waves.

References

[1] LEE K H, CHO S, KIM K T, KIM J G, LEE P S. Hydroelastic analysis of floating structures with liquid tanks and comparison with experimental tests [J]. Applied Ocean Research, 2015, 52: 167-187.

[2] MIRAFZALI F, TAVAKOLI A, MOLLAZADEH M. Hydroelastic analysis of fully nonlinear water waves with floating elastic plate via multiple knot B-splines [J]. Applied Ocean Research, 2015, 51: 171-180.

[3] MANDAL S, DATTA N, SAHOO T. Hydroelastic analysis of surface wave interaction with concentric porous and flexible cylinder systems [J]. Journal of Fluids and Structures, 2013, 42: 437-455.

[4] MICHAILIDES C, LOUKOGEORGAKI E, ANGELIDES D C. Response analysis and optimum configuration of a modular floating structure with flexible connectors [J]. Applied Ocean Research, 2013, 43: 112-130.

[5] STENIUS I, A, BATTLEY M, ALLEN T. Experimental hydroelastic characterization of slamming loaded marine panels [J]. Ocean Engineering, 2013, 74: 1-15.

[6] MICHAEL H M. The time-dependent motion of a floating elastic or rigid body in two dimensions [J]. Applied Ocean Research, 2014, 46: 54-61.

[7] FUAT K. Time domain prediction of hydroelastic of floating bodies [J]. Applied Ocean Research, 2015, 51: 1-13.

[8] Lloyd’s Register. General information for the rules and regulations for the classification of naval ships [S]. UK: Provisional Rules for the Classification of Naval Ships, 2010.

[9] TIAN Chao. Theoretical and applicational study on the nonlinear hydroelastic of ships with forward speed [D]. China: Shanghai Jiao Tong University, 2007. (in Chinese)

[10] ZOU Ming-song. Three-dimensional sono-elasticity of ships [D]. Wuxi, China: China Ship Research & Development Academ, 2014. (in Chinese)

[11] XIAO Yue, WANG Yan-ying. The time-domain analysis for the 3-D moored system [J]. China Ocean Engineering, 2004, 18(3): 433-444.

[12] NEWMAN N, LEE C H. WAMIT manual [R]. Chestnut Hill: WAMIT Inc., 2007.

[13] CHEN Xiao-bo. HydroStar manual [R]. Paris: Research Department BUREAU VERITA, 2007.

[14] KIM J H, KIM Y H, KOROBKIN A. Comparison of fully coupled hydroelastic computation and segmented model test results for slamming and whipping loads [J]. International Journal of Naval Architecture and Ocean Engineering, 2014, 6: 1064-1081.

[15] KIM Y, AHN I G, PARK S G. Extraction of the mode shapes of a segmented ship model with a hydroelastic response [J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7: 979-994.

[16] A, KAPSENBERG G. Design of a ship model for hydro-elastic experiments in waves [J]. International Journal of Naval Architecture and Ocean Engineering, 2014, 6: 1130-1147.

[17] REN Hui-long, CHEN Zhan-yang. Effect of self propulsion and towing test on ship load response [J]. Huazhong Univ of Sci & Tech: Natural Science Edition, 2012, 40 (11): 84-88. (in Chinese)

[18] CUMMINS W. The impulse response function and ship motions [J]. Schisfftechnik, 1962, 9: 101-109.

[19] CAO Yu-song. A procedure for evaluation, assessment and improvement of added mass and radiation damping of floating structures [C]// The 27th International Conference on Offshore Mechanics and Arctic Engineering. Portugal, 2008.

[20] JIAO Jia-long, REN Hui-long, SUN Shu-zheng, ADENYA C A. Investigation of a ship’s hydroelasticity and seakeeping performance by means of large-scale segmented self-propelling model sea trial [J]. Journal of Zhejiang University: Science A (Applied Physics & Engineering), 2016, 17(5): 468-484.

(Edited by FANG Jing-hua)

Cite this article as: CHEN Zhan-yang. A nonlinear hydroelastic method considering wave memory effect for ship load responses in irregular waves [J]. Journal of Central South University, 2017, 24(9): 2058–2070. DOI: https://doi.org/ 10.1007/s11771-017-3615-5.

Foundation item: Project(51509062) supported by the National Natural Science Foundation of China; Project(ZR2014EEP024) supported by the Shandong Provincial Natural Science Foundation, China; Project(HIT.NSRIF.201727) supported by the Fundamental Research Funds for the Central Universities, China

Received date: 2016-02-29; Accepted date: 2016-10-06

Corresponding author: CHEN Zhan-yang, Lecturer, PhD; Tel: +86-13506318766; E-mail: chen_1228@163.com