DOI: 10.11817/j.issn.1672-7207.2015.06.012

基于改进半监督局部保持投影算法的故障诊断

杨望灿，张培林，吴定海，陈彦龙

(军械工程学院 七系，河北 石家庄，050003)

摘要：为解决在少量标记样本的条件下故障诊断困难的问题，提出一种基于改进半监督局部保持投影(ISS-LPP)的故障诊断方法。ISS-LPP算法利用部分标记样本的标签信息调整原始特征空间中样本间的权值矩阵，并根据所有样本在特征空间的分布情况自适应的调整邻域参数，寻找数据的低维本质流形，得到原始特征空间样本数据的低维特征向量和投影转换矩阵。以得到的低维特征向量为输入，建立分类器，识别和判断故障类型。将ISS-LPP算法应用于滚动轴承的故障诊断。实验结果表明：该方法能够在标记样本较少时，提高轴承的故障诊断精度。

关键词：故障诊断；改进半监督局部保持投影；权值矩阵；邻域参数；滚动轴承

中图分类号：TH113.1；TH165.3             文献标志码：A         文章编号：1672-7207(2015)06-2059-06

Fault diagnosis based on improved semi-supervised locality preserving projections

YANG Wangcan, ZHANG Peilin, WU Dinghai, CHEN Yanlong

(Seventh Department, Ordnance Engineering College, Shijiazhuang 050003, China)

Abstract: In order to diagnose the fault effectively with a small number of labeled samples, a method of fault diagnosis based on improved semi-supervised locality preserving projections was proposed. The method of ISS-LPP used the information of some labeled samples to adjust the weight matrix among all samples in the original characteristic space. The neighborhood parameter could be adjusted automatically according to the distribution of the all samples. Therefore, the low-dimensional manifold could be found. So the low-dimensional eigenvectors and the projection matrix were achieved from the original characteristic space by ISS-LPP. With the low-dimensional eigenvectors as inputs, classifiers were established for identifying fault types. The method of ISS-LPP was applied for the fault diagnosis of roller bearing. The results indicate that the proposed method can diagnose bearing fault in high accuracy with a small number of labeled samples.

Key words: fault diagnosis; improved semi-supervised locality preserving projections; weight matrix; neighborhood parameter; roller bearing

目前，机械设备结构日益复杂化，设备运行监测数据蕴含了设备运行状态的全部信息。如何从这些数据信息中准确有效地获知和判断设备的运行状态和故障类型是故障检测和诊断的关键环节^[1]。面对获取的监测数据信息，能够比较容易地收集大量无标签的样本，而对故障样本的类别标记需耗费大量的时间、人力和物力，并且需要一定的专家知识，如何利用少量标记样本和大量无标签的样本进行学习在故障诊断领域引起了广泛的关注^[2-4]。半监督学习就是研究怎样综合利用少量有标签样本和大量无标签样本的信息来提高故障诊断精度。在旋转机械故障诊断中，通过传感器采集和提取振动加速度信号是应用较为广泛的方法，但采集到的振动信号通常具有非线性、非平稳特征^[5-6]。针对振动信号，可以从时域、频域和时频域等方面提取反映机械设备运行状态的量化指标，但随着特征参数的增多，故障诊断过程中就需要处理较大的数据信息量，因此，如何从“高维数、非线性”的特征数据空间中提取最能反映机械运行状态的本质流形特征显得非常关键。自Tenenbaum等^[7-9]先后提出流形学习的概念和方法后，流形学习成为一类重要的维数约减方法。流形学习比传统的线性降维方法更能体现数据的内在本质，因此，流形学习方法在人脸识别、图像处理和故障诊断等方面得到了广泛的应用^[10-12]。局部保持投影(LPP)算法通过线性逼近LE，兼有线性降维方法优点和经典流形学习算法的非线性化处理能力，而且能够得到显式的投影矩阵，提高了流形学习算法的泛化能力^[13-14]。但传统的LPP算法属于无监督的流形学习方法，不能有效利用样本标签的有用信息指导降维过程，而有监督的LPP算法要求大量的带标签样本，成本过高，而且有时在实际故障诊断中很难获得大量标记样本。因此，本文作者提出了一种基于改进半监督局部保持投影(ISS-LPP)的故障诊断方法。该方法在对所有样本原始特征子集进行维数约减的同时，充分利用带有标签的样本，重新构建原始特征空间中样本间的权值矩阵，使得同类样本点在低维特征空间中距离更近，不同类样本点距离更远，从而得到有利于分类的低维特征向量和投影转换矩阵。针对半监督局部保持投影算法中需要根据经验人为设定全局的邻域参数，ISS-LPP算法能够根据原始特征空间中样本的分布情况自适应地调整邻域参数，更好地获取数据的低维本质流形。最后，将运用ISS-LPP算法得到的低维特征向量输入分类器，判断和识别故障类型。通过对滚动轴承故障振动信号的分析，验证了ISS-LPP算法的可行性和有效性。

1  局部保持投影(LPP)算法

局部保持投影算法本质上是一种线性的流形学习方法，但它继承了非线性流形学习中拉普拉斯映射(LE)的思想，是LE的线性逼近，所以具有一般线性降维方法所不具有的流形学习能力。LPP算法依据最近邻图建立映射，其思想是在特征降维的同时，保持数据局部结构特征不变，即在高维空间中距离相近的点映射到低维空间中也相距较近。

假设在高维空间R^D中有一个数据集X= {x₁，x₂，…，x_N}，LPP的目的是寻求一个投影转换矩阵A，使得高维空间中的数据集X映射到相对低维的特征空间R^d(d＜＜D)中，数据集在R^d中表示为Y= {y₁，y₂，…，y_N}，即通过Y=A^TX，将数据集X映射为Y。投影转换矩阵A通过最小化下面的目标函数得到：

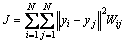            (1)

其中：W_ij为权值矩阵W的一个元素。权值矩阵W基于谱图理论，通过近邻图G来度量无标记数据间的相似度。对于样本点x_i∈R^D，根据邻域参数ε找到其邻域点集合，记为N_ε(x_i)。若x_j∈N_ε(x_i)，则用一条边连接近邻图G中点x_i和x_j，并给该边赋予一个权值。因此根据图G，构建权值矩阵W，具体定义如下式所示：

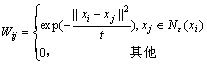      (2)

其中：参数t＞0，为热核宽度。

由式(1)和(2)可得：LPP算法通过目标函数的最小化保持数据点间的局部结构特征，即在高维特征空间相距较近的点投影到低维特征空间也相距较近。对目标函数最小化的推导过程如下

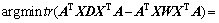
           (3)

式(3)中矩阵D是一个N×N的对角阵，其对角线元素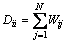，L=D-W为拉普拉斯矩阵，表示无标记数据的局部结构。

引入约束条件YDY^T=1，即A^TXDX^TA=1，则式(3)的最优化问题可转化为求解下式的广义特征值问题

XLX^TA=λXDX^TA              (4)

令列向量a₁，a₂，…，a_d分别为式(4)的前d个最小非零特征值对应的特征向量，则投影转换矩阵A的表达式如下式所示

A={a₁，a₂，…，a_d}           (5)

通过LPP算法，高维空间的数据集转化到低维特征空间中，有效的保持样本数据的局部流形结构，并且能够得到显式的投影转换矩阵A，但LPP算法存在以下问题：

1) LPP算法中邻域参数的选择直接影响算法的性能，但LPP算法通过人为经验设定一个统一的全局邻域参数ε，造成所构建的邻域图不能满足LPP算法对邻域的要求。

2) LPP算法属于无监督的学习方式，只是依据样本数据点空间距离的远近实现维数约减，无法利用部分标记样本寻找更能体现数据本质的低维流形。

2  改进半监督局部保持投影(ISS- LPP)算法

2.1  邻域参数的自适应调整

保持邻域的局部结构是LPP算法对邻域的基本要求。LPP设定的是一个统一的全局邻域参数，而实际采集到的数据样本在空间分布往往并不均匀，所以若根据数据样本的空间分布自适应的调整邻域参数的大小，则得到的低维特征向量更能反映数据的内在流形。Parzen窗概率密度估计^[15]是一种非参数的概率密度估计方法，能够依据数据样本估计出样本的空间分布，所以，利用Parzen窗估计出样本的概率密度来自适应调整邻域参数ε。

高维空间R^D中存在一个数据集X={x₁，x₂，…，x_N}，对于任一数据点x_i(i=1，2，…，N)，基于Parzen窗的概率密度估计式为

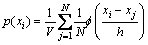         (6)

其中：N为数据集的样本个数，h为窗体宽度，V=h^D为窗体体积，为窗函数，且满足≥0，

。

假设LPP算法中邻域参数初始值为ε₀，则样本点x_i的初始邻域为N_ε0(x_i)，若令Parzen窗的窗宽h=ε₀，窗函数选择正态窗函数

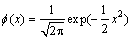           (7)

则点x_i的邻域概率密度为

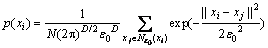  (8)

根据估计的邻域概率密度通过下式调整邻域参数ε。

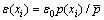             (9)

其中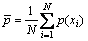：为数据集的平均概率密度。

分析式(9)可以得到：当数据点的密度较小时，即其邻域空间较稀疏时，自动地减小ε，保持邻域的局部线性结构；当数据点的密度较大时，即其邻域空间较密集时，又能自动地增大ε，使相连的邻域尽可能重叠，保证数据集全局结构的恢复。

2.2  半监督局部保持投影(SS-LPP)算法

将半监督学习思想引入局部保持投影(LPP)算法，一方面能够利用大量的未标记样本，使得数据空间更加稠密，避免了样本数量较少时的“过训练”和“过拟合”问题，提高学习模型的泛化能力；另一方面由于具有相同标签的点具有相同的结构流形，具有不同标签的点结构流形不同，因此，利用部分标记样本能更有效地寻找高维数据空间中的本质流形。SS-LPP算法在构建权值矩阵时，利用部分标签信息使邻域中具有相同标签的数据点间的权重增大，具有不同标签的数据点间的权重置零，从而使重建的权值矩阵能够更准确地刻画数据的局部特性。

高维空间R^D中存在一个数据集X={x₁，x₂，…，x_l，x_l+1，…，x_l+u}，l+u=N。其中，X_l={x₁，x₂，…，x_l}是l个有标签的样本，其对应的标签为{z₁，z₂，…，z_l}，标签集合Z={1，2，…，c}，共有c种类别，X_u= {x_l+1，x_l+2，…，x_l+u}是u个无标签的样本。假设x_j为样本点x_i(i=1，2，…，l)邻域中的一个点，若x_j有标签，且和x_i具有相同的标签，则增加x_i和x_j之间的权重，即增大权值W_ij，使该点对目标函数的最小化发挥更大的作用；若x_j有标签，且和x_i具有不同的标签，则去掉x_i和x_j之间的连接边，即将权值W_ij置0，使该点不对目标函数的最小化发挥作用；若x_j没有标签，则权值W_ij保持不变。重新构建的权值矩阵W如下所述：

若x_i∈X_l，x_i的邻域为N_ε(x_i)，则

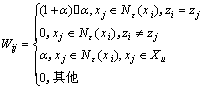       (10)

若x_i∈X_u，x_i的邻域为N_ε(x_i)，则

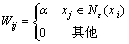             (11)

式(10)和式(11)中。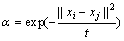

2.3  改进半监督局部保持投影(ISS-LPP)算法流程

改进半监督局部保持投影(ISS-LPP)算法的具体步骤如下：

ISS-LPP算法：

输入：高维空间数据样本集X={(x₁，z₁)，(x₂，z₂)，…，(x_l，z_l)，x_l+1，…，x_l+u}，x_i∈R^D，z_i∈R为样本标签，低维特征空间维数d

输出：低维特征向量Y，投影转换矩阵A

1) 设定邻域参数初始值ε₀，根据式(8)和式(9)计算调整后的邻域参数ε(x_i)；

2) 利用标记样本和未标记样本，根据邻域参数ε(x_i)、式(10)和式(11)构建权值矩阵W；

3) 根据重新构建的权值矩阵W，求解特征方程XLX^TA=λXDX^TA中的前d个最小非零特征值对应的特征向量，构成投影转换矩阵A={a₁，a₂，…，a_d}；

4) 根据映射Y=A^TX，得到低维特征向量Y。

3  滚动轴承的故障诊断应用

3.1  诊断对象及其原始特征空间的构建

以振动实验台中的滚动轴承为故障诊断对象，验证改进半监督局部保持投影(ISS-LPP)算法的有效性。滚动轴承故障主要有外圈故障、内圈故障和滚动体故障，每种故障会使轴承产生不同特征的振动情况。实验中将加速度传感器安装在故障轴承的轴承座上，采集正常状态和不同故障状态下的轴承振动信号。电动机转速控制在1 770 r/min左右，采样频率为12 kHz。分别采集正常、外圈故障、内圈故障和滚动体故障4种状态的振动数据各120组，每组数据的采样点数为1 024个。其中，随机选取每种状态的40组数据作为新增样本。4种状态轴承振动信号的时域波形如图1所示。

分析图1可知：4种不同状态下振动信号的振动特征略有不同，但差别不是很大，并且受到噪声干扰。因此，本文利用时域特征指标和小波包分解构建轴承故障诊断的时域和频域的原始特征向量，得到轴承不同状态的较为全面的数据信息。

根据滚动轴承典型故障的诊断特点，选择均值、方根幅值、标准差、有效值、峰峰值、波形指标、脉冲指标、偏斜度、峭度和裕度指标等10个对故障敏感的时域特征参数来全面描述振动信号的时域特征。由于这10个特征参数包含有量纲和无量纲的特征参数，所以对每个样本的时域特征参数进行归一化处理。针对时域特征参数的局限性，采用db4小波包函数对原始振动信号进行5层正交小波包分解，根据分解出的各频带信号与原始振动信号的能量比作为振动信号的频域特征参数。因此，共构造42个统计特征指标来描述轴承的不同状态，组成原始特征空间的数据集。

3.2  应用结果

按照ISS-LPP算法的具体步骤，对所构建的原始特征空间进行维数约减，寻找原始特征空间的低维流形，得到输出结果。将输出结果输入分类器，判断故障类型，验证实验效果。分类器选择最小二乘支持向量机(LS-SVM)。为了验证本文算法的有效性，分别采用主成分分析(PCA)和局部保持投影(LPP)算法对原始特征空间的数据集进行维数约减，作为对比实验。

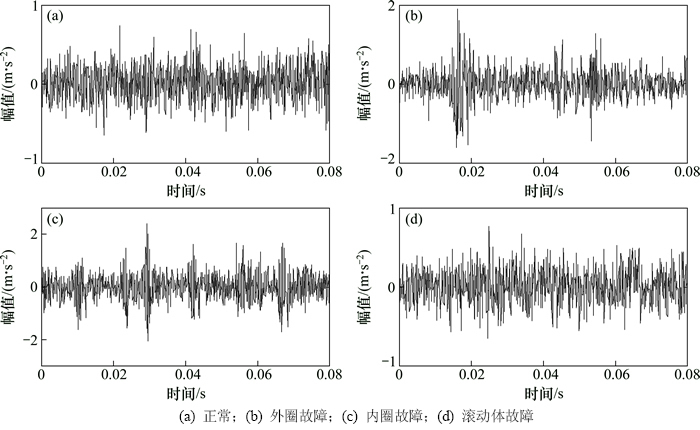
图1  4种状态的振动信号

Fig. 1  Vibration signals of four states

实验过程中，LPP算法中的邻域参数ε设定为1，ISS-LPP算法中邻域参数初始值ε₀设定为1，2种算法中的热核宽度t均设定为8。为了测试ISS-LPP算法中标记样本与未标记样本的不同比例对降维效果的影响，将原始特征空间的数据样本按照标签样本数与未标签样本数比例为1:3，1:1，和3:1的比例随机进行分配。分类器LS-SVM使用径向基核函数，采用交叉验证的方法优化核函数参数σ²和惩罚因子γ，从而得到最终的实验结果。实验结果如图2所示。

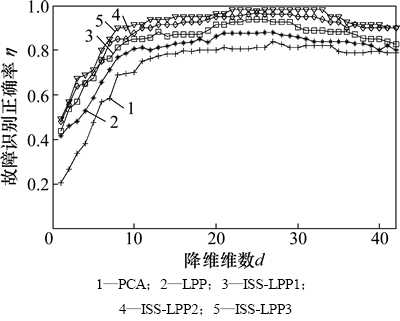
图2  故障识别正确率与低维特征空间维数的关系

Fig. 2  Relationship between fault recognition rate and dimension of low-dimension eigenspace

图2中ISS-LPP1代表ISS-LPP算法中标记样本与未标记样本的比例为1:3，ISS-LPP2代表ISS-LPP算法中标记样本与未标记样本的比例为1:1，ISS-LPP3代表ISS-LPP算法中标记样本与未标记样本的比例为3:1。从图2可以看出：无论是PCA，LPP还是ISS-LPP算法，在维数约减的初始阶段，随着降维维数的增加，故障识别的正确率逐步提高。在降维维数为25维左右时，各种算法的故障识别正确率基本达到了各自算法比较理想的故障识别正确率。由图2可知：PCA算法的故障识别正确率最低，这是由于PCA算法基于二阶统计信息，将多维数据转换到数据最大方差集方向，实质上是对坐标的一种线性变换，忽略了原始特征空间的非线性结构，因此降维效果较差。LPP算法故障识别正确率明显高于PCA算法，因为LPP通过构建最近邻图，保持原始特征空间的局部结构，寻找数据空间的低维流形，因此效果好于PCA算法。但LPP算法属于无监督模式，没有考虑标签的类别信息，且选取的邻域参数ε是全局统一固定的邻域参数，所以故障识别正确率低于ISS-LPP算法。ISS-LPP算法在构建权值矩阵时，通过部分标记样本的标签信息，强调类别之间的差异来突出鉴别性能，而且根据原始特征空间中的样本分布自适应调整邻域参数，所以ISS-LPP效果优于LPP和PCA算法。随着标记样本数量的增加，从样本中获得的先验信息越全面，能够更准确的发现原始特征空间的内在规律，因此ISS-LPP算法的故障识别的准确率也随之提高。表1列出各种算法的最高故障识别正确率和对应的降维维数。

表1  各种算法的最高故障识别正确率

Table 1  Highest fault recognition rate of each algorithm

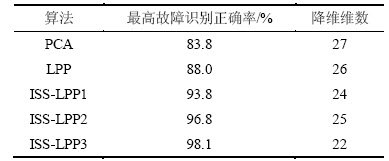
通过对比实验结果可得：ISS-LPP算法利用部分标记样本的标签信息和邻域参数的自适应调整，使最高故障识别正确率得到了较大地提高。

由于ISS-LPP算法得到显式的投影转换矩阵，能够快速地处理新增数据样本，所以将随机选取的每种状态的40组原始特征空间的新增样本，利用最高故障识别正确率对应的投影转换矩阵，将高维数据样本转换为低维特征向量，并输入LS-SVM分类器，验证实验效果。投影转换矩阵选择ISS-LPP算法中标记样本和未标记样本比例为1:3时得到的投影转换矩阵。同时作为对比，直接将原始特征空间的数据输入LS-SVM分类器，得到如表2所示的实验结果。

表2  新增样本的故障诊断结果

Table 2  Fault diagnosis results of new samples

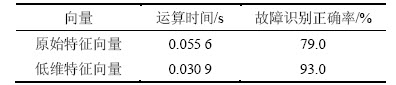
由表2可得：由于原始特征空间中的特征参数存在一些与故障诊断无关或是相互冗余的特征，所以故障识别正确率只有79%。而利用ISS-LPP对原始特征空间进行维数约减，得到原始数据特征的本质流形，因此故障识别正确率提高到93%。在运算时间方面，利用低维特征向量对故障进行诊断，能够减少运算时间，提高故障诊断的效率。

4  结论

针对故障诊断中有标记样本较少的问题，提出了一种基于改进半监督局部保持投影(ISS-LPP)的故障诊断方法。该方法充分利用部分标记样本的标签信息构建权值矩阵，并利用Parzen窗估计样本的空间分布来调整邻域参数，使得到的低维特征向量和投影转换矩阵更能反映原始特征空间数据的本质流形。将ISS-LPP算法应用在由时域特征参数和小波包分解得到的频域特征参数构成的原始特征空间中，充分挖掘数据信息的内在规律，得到对故障敏感的低维特征向量和投影转换矩阵。得到的低维特征向量输入LS-SVM分类器，识别和判断轴承故障，得到的投影转换矩阵能快速有效地处理新增数据。通过与其他方法的实验对比，实验结果表明本文方法能够有效地应用于滚动轴承的故障诊断，提高轴承故障诊断的准确率。

参考文献：

[1] 盛兆顺, 尹琦玲. 设备状态监测与故障诊断技术及应用[M]. 北京: 化学工业出版社, 2003: 1-10.

SHENG Zhaoshun, YIN Qiling. Equipment condition monitoring and fault diagnosis technology and its application[M]. Beijing: Chemical Industry Press, 2003: 1-10.

[2] 陶新民, 曹盼东, 宋少宇, 等. 基于两阶段学习的半监督SVM故障检测方法[J]. 振动与冲击, 2012, 23(31): 39-43.

TAO Xinmin, CAO Pandong, SONG Shaoyu, et al. Fault detection based on two-stage learning and semi-supervised SVM[J]. Journal of Vibration and Shock, 2012, 23(31): 39-43.

[3] ZHAO Xiukuan, LI Min, XU Jinwu, et al. An effective procedure exploiting unlabeled data to build monitoring system[J]. Expert Systems with Application, 2011, 38(8): 10199-10204.

[4] 尹刚, 张英堂, 李志宁, 等. 基于在线半监督学习的故障诊断方法研究[J]. 振动工程学报, 2012, 25(6): 637-642.

YIN Gang, ZHANG Yingtang, LI Zhining, et al. Fault diagnosis method based on online semi-supervised learning[J]. Journal of Vibration Engineering, 2012, 25(6): 637-642.

[5] 赵志宏, 杨绍普. 基于小波包变换与样本熵的滚动轴承故障诊断[J]. 振动、测试与诊断, 2012, 32(4): 640-644.

ZHAO Zhihong, YANG Shaopu. Roller bearing fault diagnosis based on wavelet packet transform and sample entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 640-644.

[6] 林近山, 陈前. 基于非平稳时间序列双标度指数特征的齿轮箱故障诊断[J]. 机械工程学报, 2012, 48(13): 108-114.

LIN Jinshan, CHEN Qian. Fault diagnosis of gearboxes based on the double-scaling-exponent characteristic of nonstationary time series[J]. Journal of Mechanical Engineering, 2012, 48(13): 108-114.

[7] Tenenbaum J B, Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290: 2319-2323.

[8] Seung H S, Daniel D L. The manifold ways of perception[J]. Science, 2000, 290: 2268-2269.

[9] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290: 2323-2326.

[10] JIE Gui, WEI Jia, LING Zhu, et al. Locality preserving discriminant projections for face and palm print recognition[J]. Neurocomputing, 2010, 73: 2696-2707.

[11] 杜海顺, 柴秀丽, 汪凤泉, 等. 一种邻域保持判别嵌入人脸识别方法[J]. 仪器仪表学报, 2010, 31(3): 625-629.

DU Haishun, CHAI Xiuli, WANG Fengquan, et al. Face recognition method using neighborhood preserving discriminant embedding[J]. Chinese Journal of Scientific Instrument, 2010, 31(3): 625-629.

[12] 杨庆, 陈桂明, 何庆飞, 等. 局部切空间排列算法用于轴承早期故障诊断[J]. 振动、测试与诊断, 2012,32 (5): 831-835.

YANG Qing, CHEN Guiming, HE Qingfei, et al. Inchoate fault diagnosis of rolling bearing based on local tangent space alignment algorithm[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 831-835.

[13] 张伟, 夏利民, 罗大庸. 正交流形保持投影方法[J]. 中南大学学报(自然科学版), 2011, 42(3): 688-692.

ZHANG Wei, XIA Limin, LUO Dayong. Orthogonal manifold preserving projections[J]. Journal of Central South University (Science and Technology), 2011, 42(3): 688-692.

[14] ZHANG Limei, QIAO Lishan, CHEN Songcan. Graph-optimized locality preserving projections[J]. Pattern Recognition, 2010, 43: 1993-2002.

[15] 边肇祺, 张学工. 模式识别[M]. 北京: 清华大学出版社, 2000: 65-71.

BIAN Zhaoqi, ZHANG Xuegong. Pattern recognition[M]. Beijing: Tsinghua University Press, 2000: 65-71.

(编辑  陈爱华)

收稿日期：2014-04-13；修回日期：2014-07-20

基金项目(Foundation item)：国家自然科学基金资助项目(E51205405)(Project (E51205405) supported by the National Natural Science Foundation of China)

通信作者：张培林，博士，教授，博士生导师，从事机械维修理论与技术的研究；E-mail：ZPL1955@163.com