文章编号:1004-0609(2011)10-2687-10
由三元相图计算活度
翟玉春
(东北大学 材料与冶金学院,沈阳 110819)
摘 要:采用熔化自由能法、标准生成自由能法和化学平衡法推导出利用8种类型的三元相图计算活度的公式,覆盖了三元相图的点、线、面全部范围。公式本身没有引进假设和近似。这8种类型的三元相图涵盖了有液相面各种类型的三元相图。本研究的计算方法和计算公式可以应用于各种复杂的三元相图,该方法也可以推广到三元等温截面相图和三元以上的多元相图。
关键词:三元相图;活度;计算;熔化自由能法;标准生成自由能法;化学平衡法
中图分类号:TF01 文献标志码:A
Activity calculation from ternary phase diaagrams
ZHAI Yu-chun
(School of Materials and Metallurgy, Northeastern University, Shenyang 110819, China)
Abstract: The activities formulas of all the points, lines and areas were calculated from the eight typical ternary phase diagrams by means of the melting point free energy method, standard free energy of formation method and chemical equilibrium method. No assumptions and approximations were introduced. The eight typical phase diagrams studied almost cover the whole range of ternary phase diagrams. The calculation methods and formulas could be applied to all kinds of complicated ternary phase diagrams. Additionally, this method could also be widely applied to the ternary isothermal section phase diagrams and multi-component phase diagrams.
Key words: ternary phase diagrams; activities; calculation; melting free energy method; standard formation free energy method; chemical equilibrium method
活度是重要的热力学数据,活度的测量,尤其是高温体系活度的测量费时、费钱、费力,且不易准确。因此,人们提出了很多办法计算活度[1-3]。由相图计算活度就是其中的一种方法。由相图计算活度有熔化自由能法和冰点下降法。目前这方面的研究已经有了一些报道[4-12],相图可以实验测定,也可以计算得 到[13-18]。现在已经积累了大量的相图,和应用关系密切的体系的相图几乎都有。相图中包含大量的信息,但并没得到充分利用,利用相图计算活度就是对相图所包含的信息进行提取。
相图的种类很多,数量更多,但有液相区存在的三元相图,即三元系投影相图可以归纳为8种类型。给出利用这8种类型相图计算活度的方法和公式,就可以应用于各种三元相图活度的计算。依据活度和温度的关系,由计算的某个温度的活度就可以得到其他温度的活度。
本文作者采用熔化自由能法、标准生成自由能法和化学平衡法计算三元相图的活度。覆盖了三元相图的点、线、面全部范围,该项工作尚未见报道,该方法可以推广到三元等温截面相图和三元以上的多元相图。
1 由三元共晶相图计算活度
图1所示为三元共晶相图。
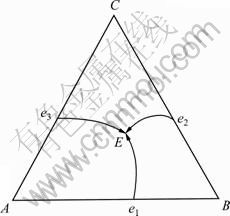
图1 三元共晶相图
Fig.1 Ternary eutectic phase diagram
1.1 液相面上活度的计算
在液相面Ae1Ee3上,固相组元A与液相L平衡共存:
L
 (1)
(1)
即
(A) A(s) (2)
A(s) (2)
在液相面上组元A与同温度固态纯A平衡。所以在液相面上,液相中组元A的化学势与同温度固态纯A的化学势相等,即
 (3)
(3)
式中: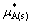 为纯固态A的化学势;
为纯固态A的化学势;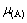 为在液相面上A的化学势。
为在液相面上A的化学势。
若组元A的活度取同温度纯液态A为标准状态,则
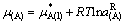 (4)
(4)
式中: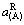 为液相面上任一点液相中组元A的活度(拉乌尔定律定义的活度);
为液相面上任一点液相中组元A的活度(拉乌尔定律定义的活度);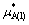 为纯液态A的化学势。所以
为纯液态A的化学势。所以
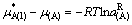 (5)
(5)
将式(1)代入式(3),得
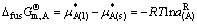 (6)
(6)
式中: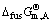 是纯A的熔化自由能,可以利用下式计算。
是纯A的熔化自由能,可以利用下式计算。
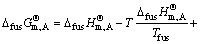
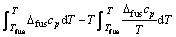 (7)
(7)
式中:Tfus为纯A的熔点;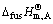 为纯A的摩尔熔化焓;
为纯A的摩尔熔化焓;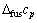 为纯A的液相和固相的定压比热容差。
为纯A的液相和固相的定压比热容差。
同理,该方法适用于计算液相面Be2Ee1B上组元B的活度和液相面Ce3Ee2C上组元C的活度。
1.2 共熔线上活度的计算
在共熔线e1E上任一点有
L A(s)+B(s) (8)
A(s)+B(s) (8)
即
(A) A(s) (9)
A(s) (9)
(B) B(s) (10)
B(s) (10)
在共熔线上,液相中组元A和B分别与纯固态A和B平衡。因而在共熔线上,A、B的化学势分别与同温度的纯固态A和B的化学势相等,即
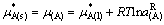 (11)
(11)
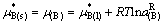 (12)
(12)
故有
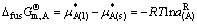 (13)
(13)
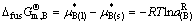 (14)
(14)
同理,该方法适用其他两条共熔线。
1.3 三元低共熔点活度的计算
在三元低共熔点E上有
L A(s)+B(s)+C(s) (15)
A(s)+B(s)+C(s) (15)
即
(A) A(s) (16)
A(s) (16)
(B) B(s) (17)
B(s) (17)
(C) C(s) (18)
C(s) (18)
在三元最低共熔点,液相与纯固态A、B和C平衡共存。因而液相中的A、B、C的化学势分别与同温度的纯固态A、B和C的化学势相等,即
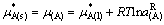 (19)
(19)
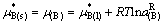 (20)
(20)
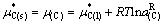 (21)
(21)
故
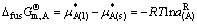 (22)
(22)
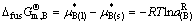 (23)
(23)
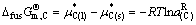 (24)
(24)
1.4 二元液相线上活度的计算
该相图的6条液相线也都是二元相图的液相线,因此具有最低共熔点的二元相图液相线上组元活度的计算方法适用于这6条液相线。
2 由具有二元同分熔点化合物的三元相图计算活度
图2所示为具有二元同分熔点化合物的三元相图。连结CD的线把三元相图ABC划分成ADC和DBC两个三元共晶相图。除化合物的D(AmBn)外,其他组元A、B、C的活度计算同于三元共晶相图。因此,下面仅讨论与化合物AmBn有关的活度计算。
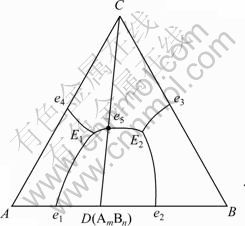
图2 具有三元同分熔点化合物的相图
Fig.2 Ternary phase diagram with tenary congruent melting compound
2.1 液相面e2E2E1e1上组元活度的计算
在析出化合物D(AmBn)的液相面e1E1E2e2上
L D(s) (25)
D(s) (25)
即
(D) D(s) (26)
D(s) (26)
因而
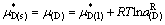 (27)
(27)
所以
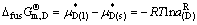 (28)
(28)
式中: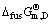 为AmBn的熔化自由能。
为AmBn的熔化自由能。
在该液相面上,还存在如下平衡
m(A)+n(B) AmBn(s) (29)
AmBn(s) (29)
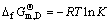 (30)
(30)
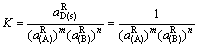 (31)
(31)
所以
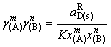 (32)
(32)
式中:K为平衡常数;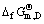 为AmBn的标准生成自由能;
为AmBn的标准生成自由能;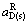 为AmBn的活度。K、
为AmBn的活度。K、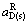 、
、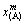 、
、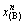 可知,所以只需得到组元A、B中任一个活度或活度因子就可以计算出另一个活度或活度因子。
可知,所以只需得到组元A、B中任一个活度或活度因子就可以计算出另一个活度或活度因子。
2.2 共熔线
在共熔线e1E1上任一点有
L A(s)+AmBn(s) (33)
A(s)+AmBn(s) (33)
即
(A) A(s) (34)
A(s) (34)
(AmBn) AmBn(s) (35)
AmBn(s) (35)
因而
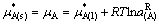 (36)
(36)
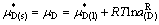 (37)
(37)
因此有
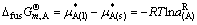 (38)
(38)
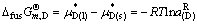 (39)
(39)
在共熔线e1E1上,还存在如下平衡
m(A)+n(B) AmBn(s) (40)
AmBn(s) (40)
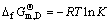 (41)
(41)
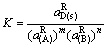 (42)
(42)
所以
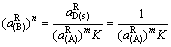 (43)
(43)
式(38)和(39)中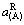 已知,而K可知,因此可以由式(43)可以求得
已知,而K可知,因此可以由式(43)可以求得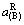 。
。
同理可求得共熔线e2E2上的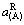 、
、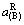 和
和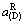 和共熔线E1E2上的
和共熔线E1E2上的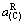 和
和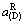 。
。
2.3 三元低共熔点
在三元低共熔点E1上有
L A(s)+C(s)+AmBn(s) (44)
A(s)+C(s)+AmBn(s) (44)
(A) A(s) (45)
A(s) (45)
(C) C(s) (46)
C(s) (46)
(AmBn) AmBn(s) (47)
AmBn(s) (47)
因而
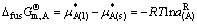 (48)
(48)
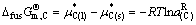 (49)
(49)
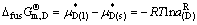 (50)
(50)
在三元低共熔点E1上,还存在如下平衡
mA+nB AmBn(s) (51)
AmBn(s) (51)
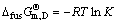 (52)
(52)
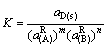 (53)
(53)
所以
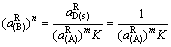 (54)
(54)
式中: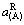 已知、K可求得,故可以由式(54)可以求得
已知、K可求得,故可以由式(54)可以求得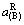 。
。
同理可求得三元低共熔点E2的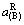 、
、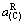 、
、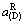 和
和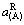 。
。
2.4 液相线
此类相图共有10条液相线,其中6条是二元系的,4条是三元系的。这里仅需讨论三元系的液相线De5和Ce5。
在液相线De5上,固相化合物AmBn和液相平衡
L AmBn(s) (55)
AmBn(s) (55)
即
(AmBn) AmBn(s) (56)
AmBn(s) (56)
因而
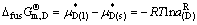 (57)
(57)
在液相线De5上,固相C和液相平衡
L C(s) (58)
C(s) (58)
即
(C) C(s) (59)
C(s) (59)
因而
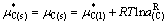 (60)
(60)
故
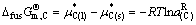 (61)
(61)
3 由具有二元异分熔点化合物的三元相图计算活度
图3所示为具有二元异分熔点化合物的三元相图。除包晶线和三元包晶点D外,其他部位组元活度计算同于具有同分熔点三元相图。因此,下面仅讨论包晶线和三元包晶点的活度计算。
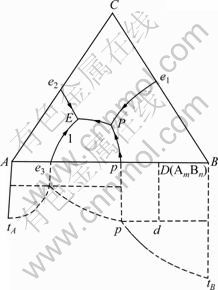
图3 具有二元异分熔点化合物的相图
Fig.3 Ternary phase diagram with binary incongruent melting compound
3.1 包晶线
在包晶线pP上,有包晶反应
L+B(s) D(s) (62)
D(s) (62)
实际化学反应为
m(A)+nB(s) D(s) (63)
D(s) (63)
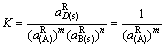 (64)
(64)
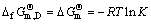 (65)
(65)
所以
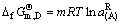 (66)
(66)
3.2 三元包晶点
在三元包晶点P处,包晶反应为
LP+B(s) D(s)+C(s) (67)
D(s)+C(s) (67)
在液相LP中,有
(B) B(s) (68)
B(s) (68)
(C) C(s) (69)
C(s) (69)
(D) D(s) (70)
D(s) (70)
并且
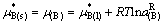 (71)
(71)
因而
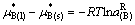 (72)
(72)
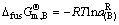 (73)
(73)
同理
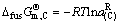 (74)
(74)
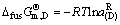 (75)
(75)
4 由具有高温稳定、低温分解的二元化合物的三元相图计算活度
具有高温稳定,低温分解的二元化合物的相图见图4。除e1P线的kP段和P点外,其他部位活度的计算都与具有二元同分熔点化合物的三元相图相同。
4.1 kP线上活度的计算
在kP线有转熔反应
LP+D(s) B(s) (76)
B(s) (76)
实际化学反应为
BmCn(s) mB(s)+n(C) (77)
mB(s)+n(C) (77)
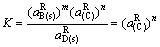 (78)
(78)
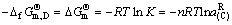 (79)
(79)
即
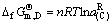 (80)
(80)
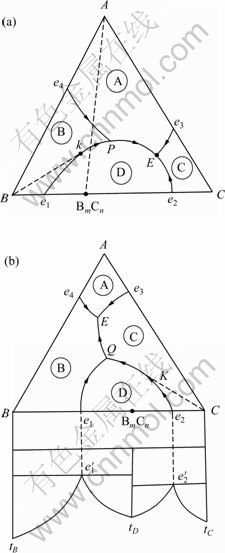
图4 具有高温稳定、低温分解的二元化合物的相图
Fig.4 Ternary phase diagram with binary compound on high temperature stability and low temperature decomposition
4.2 P点活度的计算
在P点有转熔反应
LP+B(s) D(s)+A(s) (81)
D(s)+A(s) (81)
实际化学反应为
mB(s)+n(C) D(s) (82)
D(s) (82)
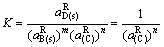 (83)
(83)
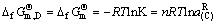 (84)
(84)
在P点还有
D D(s) (85)
D(s) (85)
(A) A(s) (86)
A(s) (86)
(B) B(s) (87)
B(s) (87)
所以
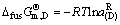 (88)
(88)
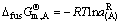 (89)
(89)
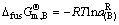 (90)
(90)
5 由具有三元同分熔点化合物的相图计算活度
图5所示为具有同分熔点的三元化合物的三元相图。该相图可以划分为3个分三元相图,组元A、B、C活度的计算与简单三元共晶相图的相同。下面讨论与三元化合物D有关部位的活度计算。
5.1 初晶区D的液相面上活度的计算
无论在哪个分三角形中,在初晶区D的液相面上,有
L D(s) (91)
D(s) (91)
即
(D) D(s) (92)
D(s) (92)
因而
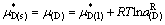 (93)
(93)
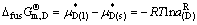 (94)
(94)
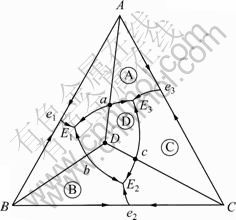
图5 具有二元同分熔点化合物的相图
Fig.5 Ternary phase diagram with binary congruent melting compound
5.2 共熔线上活度的计算
在共熔线E1a上,有
L A(s)+D(s) (95)
A(s)+D(s) (95)
(A) A(s) (96)
A(s) (96)
(D) D(s) (97)
D(s) (97)
因而
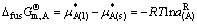 (98)
(98)
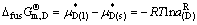 (99)
(99)
在共熔线E1a上存在如下平衡
m(A)+n(B)+p(C) D(s) (100)
D(s) (100)
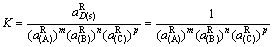 (101)
(101)
式中:K和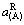 可知,若得到了组元B和C中任一个活度,即可求出另一个活度。
可知,若得到了组元B和C中任一个活度,即可求出另一个活度。
6 由具有三元异分熔点化合物的相图计算活度
图6所示为具有异分熔点化合物的三元相图。除转熔线E1p和转熔点p外,其他部位活度的计算与具有同分熔点三元化合物的相图相同。因此,下面仅讨论转熔线和转熔点的活度计算。
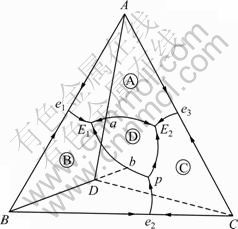
图6 具有异分熔点化合物的相图
Fig.6 Ternary phase diagram with incongruent melting compound
6.1 转熔线E1p上活度的计算
液相线E1p为转熔线,发生转熔反应
L+B(s) D(s) (102)
D(s) (102)
实际化学反应为
m(A)+nB(s)+p(C) AmBnCp(s) (103)
AmBnCp(s) (103)
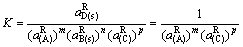 (104)
(104)
平衡常数K可知,因此只要知道组元A和C中的一个活度,就可以求出另一个活度。
在转熔线E1P中,有
(B) B(s) (105)
B(s) (105)
(D) D(s) (106)
D(s) (106)
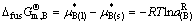 (107)
(107)
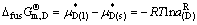 (108)
(108)
6.2 三相点p上活度的计算
在p点发生包晶反应
Lp+B(s) D(s)+C(s) (109)
D(s)+C(s) (109)
实际的化学反应为
m(A)+nB(s)+p(C) AmBnCp(s)+C(s) (110)
AmBnCp(s)+C(s) (110)
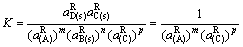 (111)
(111)
式中:如果K和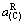 可知,
可知,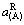 的活度可以求得。
的活度可以求得。
在P点有
(B) B(s) (112)
B(s) (112)
(C) C(s) (113)
C(s) (113)
(D) D(s) (114)
D(s) (114)
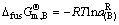 (115)
(115)
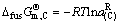 (116)
(116)
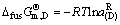 (117)
(117)
7 由具有包晶和固溶体的相图计算活度
图7所示为具有由包晶和固溶体的三元相图。除共熔线e1p、e2p、包晶线PI,包晶点P外,其他部位活度的计算与具有二元异分熔点的二元的化合物的相图相同。
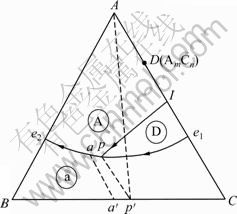
图7 有包晶和固溶体的三元相图
Fig.7 Ternary phase diagram with poritectic and solid solution
7.1 共熔线e1p上活度的计算
在共熔线e1p上,有如下平衡
L D(s)+
D(s)+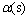 (118)
(118)
即有
(A) (A)s (119)
(A)s (119)
(B) (B)s (120)
(B)s (120)
(C) (C)s (121)
(C)s (121)
(D) (D)s (122)
(D)s (122)
m(A)+n(C)=AmCn (123)
式中:(A)s和(C)s分别表示固溶体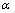 中的组元A和C。由上述平衡,得
中的组元A和C。由上述平衡,得
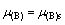 (124)
(124)
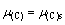 (125)
(125)
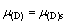 (126)
(126)
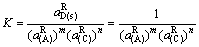 (127)
(127)
由于
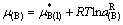 (128)
(128)
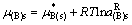 (129)
(129)
所以
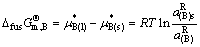
 (130)
(130)
将固溶体看作理想溶液,则
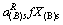 (131)
(131)
因此,
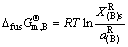 (132)
(132)
由于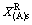 可测,所以可利用式(132)计算
可测,所以可利用式(132)计算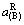 。
。
同理,有
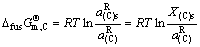 (133)
(133)
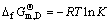 (134)
(134)
由式(127)和(134)可得
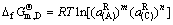 (135)
(135)
在共熔线e2p线上,有
L A(s)+
A(s)+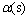 (136)
(136)
即
(A) A(s) (137)
A(s) (137)
(B) (B)s (138)
(B)s (138)
(C) (C)s (139)
(C)s (139)
对于组元A,有
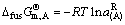 (140)
(140)
组元B、C的活度计算同e1p线。
7.2 包晶线上活度的计算
在包晶线Ip上,有
L+A(s) AmCn(s) (141)
AmCn(s) (141)
即有
(A) A(s) (142)
A(s) (142)
m(A)+n(C) AmCn(s) (143)
AmCn(s) (143)
所以
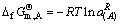 (144)
(144)
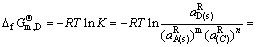
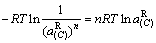 (145)
(145)
7.3 P点活度的计算
在四相点p发生三元转熔反应
Lp+D(s) A(s)+
A(s)+ (146)
(146)
即存在如下平衡
(A) A(s) (147)
A(s) (147)
(B) (B)s (148)
(B)s (148)
(C) (C)s (149)
(C)s (149)
mA(s)+n(C)s  AmCn(s) (150)
AmCn(s) (150)
活度的计算同前。
8 由具有液相分层区的相图计算活度
图8所示为具有液相分层区的三元相图。除液相分层区外,其他部位活度的计算同于三元共晶相图。
图8 有液相分层的三元相图
Fig.8 Ternary phase diagram with liquid phase delamination
8.1 液相分层界线上活度的计算
在液相分层界线上,A饱和,有
 A(s) (151)
A(s) (151)
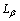
 A(s) (152)
A(s) (152)
即
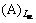
 A(s) (153)
A(s) (153)
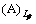
 A(s) (154)
A(s) (154)
因而
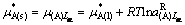 (155)
(155)
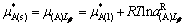 (156)
(156)
故
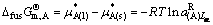 (157)
(157)
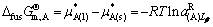 (158)
(158)
8.2 液相分层区
在液相分层区,Lα和Lβ平衡共存,并与A(s)平衡共存。因此,在液相分层区上两式仍然成立。并有
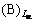

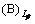 (159)
(159)
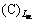

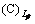 (160)
(160)
可以利用已知一个组元的活度求另外两个组元活度的方法求得组元B和C的活度。
9 结论
1) 利用含有液相区的8种类型三元相图计算活度,采用熔化自由能法、标准生成自由能法和化学平衡法推导出在三元相图点、线、面不同位置的活度计算公式,公式本身是准确的。
2) 由于8种类型的三元相图涵盖了含有液相区的各种三元相图,因此,这些计算方法和计算公式具有普适性,可以应用于各种复杂的三元相图。
3) 这些计算方法和计算公式可以推广到三元等温截面相图,也可以推广到三元以上的多元系相图。
REFERENCES
[1] CHEN D, DONG L, BAI C, LIU Q, WANG C. 
 New method for calculating the activity of stable compound from binary phase diagram[J]. Rare Metal, 2006, 25: 448-451.
New method for calculating the activity of stable compound from binary phase diagram[J]. Rare Metal, 2006, 25: 448-451.
[2] WU Y, DU W, NIE Z, CAO L, ZUO T. Thermodynamic calculation of intermetallic compounds in AZ91 alloy containing calcium[J]. Transactions of Nonferrous Metals Society of China, 2006, 16: 392-396.
[3] CHOU K C, WANG J. Calculating activities from the phase diagram involving an intermediate compound using its entropy of formation[J]. Metallurgical and Materials Transactions A, 1987, 18: 323-326.
[4] KOBERTZ D, HILPERT K, KAPALA J, MILLER M. Phase diagram, thermodynamic activities and thermodynamic modeling in the NaBr-DyBr3 system[J]. CALPHAD, 2004, 28: 203-208.
[5] HILPERT K, MILLER M. Determination of the thermodynamic activities of NaBr and DyBr3 in the phases of the NaBr-DyBr3 system at 863 K by Knudsen effusion mass spectrometry[J]. Journal of Alloys and Compounds, 2004, 379: 1-7.
[6] CHEN D F, DONG L Y, BAI C G, LIU Q C, WANG C J. A new method for calculating the activity of stable compound from binary phase diagram[J]. Rare Metal, 2006, 25: 448-451.
[7] HINO M, NAQASAKA T, BAN-YA S. Activity of phosphorus in α-Fe and phase diagram of Fe-Fe2P system above 1 273 K[J]. Zeitschrift fur Metallkunde, 1997, 88: 938-944.
[8] SRIDHAR S, PAL U B, CHOU K. Relationship between activity and three phase boundary in the ternary phase diagram[J]. CALPHAD, 1999, 23: 165-172.
[9] CHOU K C, CHEN S. Calculating activities from phase diagram containing equilibrium between solid and liquid solutions[J]. CALPHAD, 1990, 14: 41-48.
[10] ZHANG Y, ZHANG X, FU C. New methods for calculating activities of components from phase diagrams in binary peritectic systems[J]. Transactions of Nonferrous Metals Society of China, 1997, 7: 47-53.
[11] CHOU K C, SEETHARAMAN S, PAL U B. Activities and ternary phase diagrams[J]. CALPHAD, 1997, 21: 483-495.
[12] ZHANG F, CHEN S, CHOU K. A new treatment for calculating activities from phase diagrams involving intermediate compounds[J]. CALPHAD, 1992, 16: 269-276.
[13] YUSENKO K V. Phase diagram of the rhenium-rhodium system: State of the art[J]. Platinum Metals Rev, 2011, 55: 186-192.
[14] ZHOU Z M, GAO J, LI F, WANG Y P, KOLBE M. Experimental determination and thermodynamic modeling of phase equilibria in the Cu-Cr system[J]. J Mater Sci, 2011, 46: 7039-7045.
[15] EICHHAMMER Y, HEYNS M, MOELANS N. Calculation of phase equilibria for an alloy nanoparticle in contact with a solid nanowire[J]. CALPHAD, 2011, 35: 173-182.
[16] EICHHAMMER Y, ROECK J, MOELANS N, IACOPI F, BLANPAIN B, HEYNS M. Calculation of the Au-Ge phase diagram for nanoparticles[J]. Arch Metall Mater, 2008, 53: 1133-1139.
[17] ARRAS E, CALISTE D, DEUTSCH T, LAN?ON F, POCHET P. Phase diagram, structure and magnetic properties of the Ge-Mn system: A first-principles study[J]. Phys Rev B, 2011, 83: 174103.
[18] HU C, ZENG Z, ZHANG L, CHEN X, CAI L. Density functional study of the phase diagram and thermodynamic properties of Zr[J]. Computation Mater Sci, 2011, 50: 835-840.
(编辑 李艳红)
基金项目:国家自然科学基金资助项目(50136020)
收稿日期:2011-05-08;修订日期:2011-07-19
通信作者:翟玉春,教授,博士;电话:024-83687731;E-mail: zhaiyc@smm.neu.edu.cn
翟玉春教授简介
翟玉春,1946年出生,博士,教授,博士生导师。1970年毕业于东北大学冶金物理化学专业并留校任教,1988年获中南大学有色金属冶金博士学位。国务院学位委员会第四、五届学科评议组成员,国家博士后管理委员会第四、五、六、七届专家组成员,国家教学名师奖获得者,“冶金物理化学”国家级精品课程负责人,冶金工程专业平台课国家级教学团队带头人,中国金属学会冶金物理化学学术委员会副主任,中国有色金属学会冶金物理化学学术委员会副主任,东北大学冶金物理化学研究所所长。享受国务院政府津贴。《过程工程学报》、《材料导报》、《微纳电子技术》、《东北大学学报》编委。获国家教学成果二等奖2项,辽宁省教学成果一等奖2项;获广东省科技进步一等奖1项,辽宁省科技进步三等奖1项,辽宁省自然科学三等奖1项。出版教材3部、专著1部,发明专利8项。主要研究领域为:冶金过程热力学、动力学和电化学,非平衡态冶金热力学,资源高附加值绿色化综合利用,材料制备的物理化学,计算物理化学。发表论文500多篇,其中SCI收录100多篇,EI收录200多篇。