基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法

梁志文，杨金民，李元旗

(湖南大学 信息科学与工程学院，湖南 长沙，410082)

摘要：针对现有贝叶斯算法应用于垃圾邮件过滤时，贝叶斯贝努利模型对邮件文本特征向量进行处理不能区分特征向量的重要性，导致邮件分类召回率低，同时还存在合法邮件被误判的风险的问题，采用贝叶斯多项式模型对特征向量进行加权处理来区分特征向量的重要性；然后，采用低风险策略来降低合法邮件被误判的风险，提出基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法。实验结果表明：对于不同数量的特征项，该算法能够有效提高邮件分类的正确率与召回率，降低合法邮件被误判的风险，并在过滤文本字符数量较大的邮件时，具有性能平稳、波动小的特点。

关键词：邮件过滤；特征提取；概率度量；多项式模型；风险评估

中图分类号：TP312           文献标志码：A         文章编号：1672-7207(2013)07-2787-06

A Bayesian spam filtering algorithm based on polynomial model and low risk

LIANG Zhiwen, YANG Jinmin, LI Yuanqi

(College of Information Science and Engineering, Hunan University, Changsha 410082, China)

Abstract: Existing Bayesian algorithms use Bernoulli model to process text features in the application to spam filtering, which does not distinguish the varying importance of various features, leading to a low recall rate in mail classification. In addition, existing Bayesian algorithms also have the risk of mis-judging legitimate mail. A Bayesian spam filtering algorithm was proposed based on the polynomial model and the low risk. The algorithm measures the weight of text features to distinguish their importance in mail classification, and then compares the probabilities that a mail respectively fall into the spam class or the normal mail class. The results show that this algorithm effectively improves the recall and precision rate of mail classification, and reduces the risk of mis-judging legitimate mail. Additionally, the algorithm is of smooth and little fluctuation when filtering mails with a large number of text characters.

Key words: mail filtering; feature extraction; probability measurement; polynomial model; risk assessment

随着互联网的迅猛发展，电子邮件由于具有通信快捷、价格便宜、操作简单的优势，已成为最受欢迎的通信工具。但是，大量垃圾邮件的存在既消耗网络资源，又浪费用户大量的时间和精力，因此，研究垃圾邮件过滤技术有重要的现实意义^[1]。针对垃圾邮件过滤而提出的基于内容的贝叶斯过滤策略^[2-3]实现自学习功能，且满足客户个性化要求，故而在垃圾邮件过滤中得到广泛应用。现有贝叶斯过滤算法假定从邮件中提取的文本特征属性是相互独立的，当实际情况满足这种假设时，分类准确度高；但是，邮件中的文本语义、语境关系很复杂，与算法假设的吻合度较低。因此，现有贝叶斯算法应用于邮件过滤时，过多地简化很多对分类有用的特征向量信息，导致判别垃圾邮件的召回率降低^[4]。为有效地利用特征向量信息，贝叶斯贝努利模型^[5]利用布尔值0和1对特征向量进行简单的加权处理，但该模型并未考虑特征向量出现的概率，只是用布尔值0和1表示特征向量在邮件中“不出现”和“出现”，并未区分重要特征向量和非重要特征向量，不能达到高效利用特征向量的目的。另外，现有贝叶斯算法应用于邮件过滤中，存在合法邮件被误判的风险^[6]。其原因在于该算法单一地构建垃圾邮件判定尺度，将含垃圾特征的邮件判定为垃圾邮件，这种方法会导致含有部分垃圾邮件文本特征的合法邮件被误判为垃圾邮件。针对上述问题，本文作者提出基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法，利用多项式模型来计算特征向量在邮件中出现的概率，以区分不同特征向量在邮件文本中的重要性，提升邮件分类的召回率。另外，在构建垃圾邮件判定尺度的同时，也构建合法邮件判定尺度，对一个邮件进行判定时，既度量其为垃圾邮件的概率，同时也度量其为合法邮件的概率，通过概率差来分类邮件，降低合法邮件被误判的风险，提升算法的正确率。

1  贝叶斯邮件分类模型

贝叶斯分类算法^[7]在对邮件进行分类时，要先将邮件模型转化为一个基于特征项的特征向量。设邮件的特征向量为X=(X₁, X₂, …, X_i,…, X_n)，其中特征向量分量X_i是指邮件的某个属性，或者邮件文本中包含的字、词、短语或者某个概念。设概率向量P=(P₁, P₂, …, P_i, …, P_n)，其中P_i表示特征分量X_i出现的概率。邮件分为2类：G_good表示正常邮件；B_bad表示垃圾邮件。给定G_good类别的邮件集合为G_good=(g₁, g₂, …, g_i, …, g_n)，其中g_i表示正常邮件；垃圾邮件集合为B_bad=(b₁, b₂, …, b_i, …, b_n)，其中b_i表示垃圾邮件。邮件E的特征向量为X^E=(x₁^E, x₂^E, …, x_i^E, …, x_n^E)，概率向量为P^E=(p₁^E, p₂^E, …, p_i^E, …, p_n^E)，其中p_i^E表示特征分量x_i^E出现的概率。邮件E属于B_bad集合的概率P(B_bad|E)为

       (1)

其中：P(E)为邮件E的特征向量X^E发生的概率；P(B_bad)为类别B_bad的先验概率，要通过样本训练得到；P(E|B_bad)为 B_bad类别中邮件E发生的条件概率。

上述公式的关键是如何计算P(E|B_bad)，本文作者通过构建贝叶斯多项式模型来进行求解。

2  贝叶斯多项式模型

在式(1)中，P(E|B_bad)的求解，现有方法是采用贝叶斯贝努利模型^[5]。该模型用布尔值0和1表示特征向量在邮件中不出现和出现，未区分重要特征向量和非重要特征向量，不能达到高效利用特征向量的目的。本文作者构建贝叶斯多项式模型估算特征向量在邮件中出现的概率来区分不同特征向量的重要性。

对邮件E，设在进行中文分词后得到的词语数量为|E|，即邮件E的长度。邮件E的特征向量为X^E=(x₁^E, x₂^E, …, x_i^E, …, x_n^E)，特征分量x_i^E在邮件E中出现的次数设为N_i。应用贝叶斯多项式模型^[8]求解式(1)中P(E|B_bad)的方法如下：

   (2)

其中：P(E)为邮件E的先验概率，可通过全概率公式^[9]计算；P(x_i^E |B_bad) 为邮件E属于B_bad类别时，特征分量x_i^E出现的概率。

上述计算模型将某个邮件文本中的特征分量的出现看作概率事件，这些概率事件的总集合反映邮件文本特征。该模型假定特征分量在同一封邮件中多次出现是相互独立，若选取数量适当的特征分量恰好反映邮件文本特征，则P(E |B_bad)具有很高可信度。式(2)中|E|!是一个很大数值，P(x_i^E|B_bad)^N_i跟N_i!比值的乘积是一个很小数值，它们的乘积是一个数学中定义的概率，即根据样本训练数据来估算邮件E属于B_bad类别的先验概率。

式(2)中P(x_i^E|B_bad)的计算要结合样本训练来实现。样本邮件包括2类邮件：垃圾邮件和合法邮件。设垃圾样本邮件集为B_bad，合法样本邮件集为G_good。在通过邮件预处理、中文分词、特征提取^[10]后，构建出合法邮件集G_good的特征分量表，以及垃圾邮件集B_bad的特征分量表。特征分量表包括2列：特征分量，特征分量在样本邮件中的出现次数。

设邮件E通过预处理、中文分词、特征提取后的特征向量为X^E =(x₁^E, x₂^E, …, x_i^E, …, x_n^E)。式(2)中P(x_i^E|B_bad)的计算方法如下：

           (3)

其中：N(x_i^E)为B_bad类别的所有邮件文本中的特征分量x_i^E出现次数，N为B_bad类别的所有邮件文本中出现的特征分量总次数。N(x_i^E)和N从特征分量表中查询得到。

3  基于最小风险的邮件分类方法

现有贝叶斯算法单一地构建垃圾邮件判定尺度，将含垃圾特征的邮件判定为垃圾邮件，应用于垃圾邮件过滤中，存在合法邮件被误判的风险。针对该问题，提出基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法。该算法同时构建垃圾邮件和合法邮件判定尺度，对一个邮件进行判定时，既度量其为垃圾邮件的概率，同时也度量其为合法邮件的概率，通过概率差来分类邮件，降低合法邮件被误判的风险。

设P(B_bad|E) 为待分类邮件E在B_bad类别中同时出现多个特征分量时，其判定为垃圾邮件的概率，根据贝叶斯多项式公式和复合概率公式 ^[11]可得：

 (4)

其中：P_i^E为特征分量X_i^E在B_bad类别中出现的概率，通过样本训练计算。

设P(G_good|E)为待分类邮件E判为合法邮件的概率，其计算方法与P(B_bad|E)计算方法类似。

基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法将P(B_bad|E)和P(G_good|E)的差值来对邮件进行分类，该差值记为：

(-1＜a＜1)      (5)

其中：P(B_bad|E)为邮件E属于垃圾邮件的概率；P(G_good|E)为其属于合法邮件概率。当0＜a＜1时，待分类邮件E属于垃圾邮件概率大于其属于合法邮件概率；随着a增大，待分类邮件E属于垃圾邮件概率增大，其判定为垃圾邮件的可信度增强。当-1＜a＜0时，待分类邮件E属于合法邮件概率大于其属于垃圾邮件概率；a越接近-1，待分类邮件E属于合法邮件概率越大，其判定为合法邮件的可信度越强。当a接近0时，表明邮件E既含垃圾邮件特征，也含合法邮件特征，需要由用户来人工判断。因此，基于a，可将邮件分为3类：垃圾邮件、合法邮件和混杂性邮件。用户可以根据实际情况确定参数a的分类阈值。

4  实验分析

在上述基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法中，采用贝叶斯多项式模型来对特征项利用率进行改进，同时采用低风险策略来对邮件进行分类，本节通过实验来验证其有效性。实验选用新西兰怀卡托大学研究开放的Weka软件^[11]来模拟垃圾邮件过滤系统。从CCERT提供的邮件样本集CDSCE^[12]中随机抽取1 500封邮件构建邮件样本库，其中包含垃圾邮件1 000封，合法邮件500封。实验方法采用常规的“十字交叉验证法”^[13]：将1 500封邮件分为10份，每份150封，选取其中的9份作为样本训练集，剩下的1份为测试集。实验以Windows平台作为操作平台，SQL Sever 2008为后台数据库。

实验采用正确率(R_Precision)和召回率(R_Recall) 2个技术指标来度量算法的性能^[14]：

          (6)

其中：A为被正确判定出的垃圾邮件数量，B为被错误判定为垃圾邮件的邮件数量。正确率越高，正确判定的垃圾邮件和合法邮件的数量就越多，将合法邮件误判为垃圾邮件的可能性越小；

          (7)

其中：A代表被正确判定出的垃圾邮件数量，C代表没被判定出的垃圾邮件数量。召回率越高，检测到的垃圾邮件越多，漏掉的垃圾邮件就越少。

实验中，首先研究2种事件模型和特征项数量对基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法的影响。利用Weka软件对9份样本训练进行训练，提取特征项建立样本特征库。用Weka软件对剩下1份测试集中的邮件进行特征提取，分别用基于贝叶斯贝努利模型和贝叶斯多项式模型的低风险贝叶斯分类器对该测试集进行测试，不断增加特征项数量。在2种模型中，特征项数量对算法召回率的影响特性如图1所示。

从图1可见：基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法在特征项数量较少时，召回率较低。其原因在于特征向量太少，不能全面反映邮件文本特征，导致文本区分度不高。随着特征项数量增加到200个时，算法召回率出现极大值。其原因在于特征分量恰好反映邮件文本特征，不同类型邮件文本区分度高。随着特征项数量增多，算法召回率下降趋于平稳。其原因在于掺杂与分类无关的特征分量，产生分类噪声干扰算法分类效果。特别是该算法假设特征分量间相互独立，特征项太多，特征分量间依赖程度增加，独立性减小，影响算法的性能。另外，该算法采用贝叶斯多项式模型估算特征项在邮件中出现的概率来区分特征项的重要性，提高特征项的利用率，提升算法的召回率。

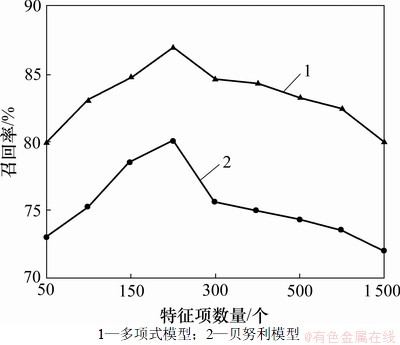
图1  不同模型下特征项数量对召回率的影响

Fig.1  Impact of feature items on recall rate in two models

实验接着研究现有贝叶斯算法和基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法对邮件分类的影响。邮件文本的中文分词和特征提取与上述实验的相同，分别用现有贝叶斯算法分类器和基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法分类器对测试集进行测试，不断增加特征项数量。在2种算法中，特征项数量对算法正确率和召回率的影响特性分别如图2和图3所示。

从图2可见：基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法的正确率比现有贝叶斯算法高。其原因在于该算法在构建垃圾邮件判定尺度的同时，也构建合法邮件判定尺度，对一个邮件进行判定时，既度量其为垃圾邮件的概率，同时也度量其为合法邮件的概率，通过概率差来分类邮件，降低合法邮件被误判的风险，提高算法分类邮件的正确率。从图3可见：基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法的召回率比简单贝叶斯算法高。其原因在于该算法采用贝叶斯多项式模型来计算特征项的概率，提高特征项的利用率。

实验最后对比研究基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法与现有贝叶斯算法^[11]的时间复杂度，主要测试邮件预处理时间(包括中文分词和特征提取所用时间)、邮件分类时间、邮件发送时间。实验选4组字符数量不同的10封邮件，分别取4组邮件的平均字符数量为4×10¹，4×10²，16×10²和4×10³，测试上述3个时间段所用的时间，取平均值为最后结果。在2种算法中，邮件文本字符数量对算法时间复杂度的影响特性如表1~4所示。

图2  2种算法的正确率对比

Fig.2  Precision comparison in two algorithms

图3  2种算法的召回率对比

Fig.3  Recall comparison in two algorithms

由测试结果可知：基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法与简单贝叶斯算法的时间复杂度为10^-4 s数量级。当邮件文本字符数为16×10²个时，基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法的邮件分类时间明显比简单贝叶斯算法少。其原因在于选取出来的特征项恰好反映邮件文本的特征，其他字符对邮件分类时间影响不大。另外，算法分类邮件次数越多，特征库的数据会不断优化，算法分类效率会不断提高。随着邮件文本字符数量增大，2种算法的邮件预处理时间、邮件分类时间、邮件发送时间随之增大，不过邮件预处理和邮件分类的时间复杂度都为10^-3 s数量级。

表1  邮件字符数为4×10¹个时的算法时间对比

Table 1  Comparison of time efficiency in algorithms at mails with 4×10¹ characters             μs

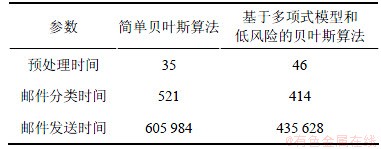
表2  邮件字符数为4×10²个时的算法时间对比

Table 2  Comparison of time efficiency in algorithms at mails with 4×10² characters             μs

表3  邮件字符数为4×10³个时的算法时间对比

Table 3  Comparison of time efficiency in algorithms at mails with 4×10³ characters             μs

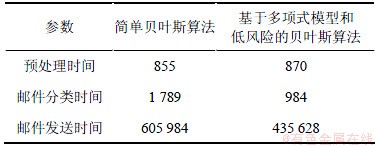
表4  邮件字符数为4×10⁴个时的算法时间对比

Table 4  Comparison of time efficiency in algorithms at mails with 4×10⁴ characters             μs

5  结论

(1) 采用多项式模型来度量邮件特征分量的权重，基于邮件分别属于垃圾类的概率与其属于合法类的概率差来对邮件进行分类，可以有效降低邮件被误判的风险。

(2) 采用贝叶斯多项式模型可以提高算法的召回率，随着特征项数量增大，算法召回率会出现极大值，并最终趋于平稳。

(3) 基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法能提高邮件分类的召回率和正确率，降低合法邮件被误判的风险，并在过滤文本字符数量较大的邮件时，具有性能平稳、波动小的特点。

参考文献：

[1] Meehan S, Susan D, David H et al. A Bayesian approach to filtering Junk e-mail[J]. AAAI Workshop, 1998, 4(13): 55-62.

[2] Kma C, Hl C, Ht N. Bayesian online classifiers for text classification and filtering[C]// Proceedings of 25th ACM International Conference on Research and Development in Information Retrieval. New York: ACM, 2002: 97-104.

[3] Sudhakar V, Rao C M, Somayajula S P K. Bayesian spam filtering using statistical data compression[J]. International Journal of Computer Science and Information Security, 2011, 9(10): 157-159.

[4] LUO Qin, LIU Bing, YAN Junhua et al. Research of a spam filtering algorithm based on naive Bayes and AIS[C]// 2010 International Conference on Computational and Information Sciences. Washington: IEEE, 2010: 152-155.

[5] 苏贵洋, 马颖华, 李建华. 一种基于内容的信息过滤改进模型[J]. 上海交通大学学报, 2004, 38(12): 2030-2034.

SU Guiyang, MA Yinghua LI Jianhua. One improved content based information filtering model[J]. Journal of Shanghai Jiaotong University, 2004, 38(12): 2030-2034.

[6] Thiago S S, Walmir M C. A review of machine learning approaches to Spam filtering[J]. Expert Systems with Applications, 2009, 36(7): 10206-10222.

[7] Lin Y P, Chen Z P, Yang X L, et al. Mail filtering based on the risk minimization Bayesian algorithm[C]// The 6th World Multi conference on Science Citation Index (SCI 2002). Proceedings-Industrial System and Engineering E, 2002, 17(2): 282-285.

[8] 林珊, 宁国宁, 赵之霖. 中文分词在邮件过滤系统中的应用[J]. 华南理工大学: 自然科学版, 2004, 32(6): 113-116.

LIN Shan, NING Guoning, ZHAO Zhiling. Application of Chinese word segmentation to anti-spam systems[J]. Journal of South China University of Technology: Natural Science Edition, 2004, 32(6): 113-116.

[9] Provost J. Naive Bayes rule-learning in classification of e-mail[R]. Texas: The University of Texas at Austin Artificial Intelligence Lab Technical Report, 1999: 5-10.

[10] 张文良, 黄亚楼, 倪维健. 基于差分贡献的垃圾邮件过滤特征选择方法[J]. 计算机工程, 2007, 33(8): 80-82.

ZHANG Wenliang, HUANG Yalou, NI Weijian. Approach to feature selection of spam filtering based on contribution difference[J]. Computer Engineering, 2007, 33(8): 80-82.

[11] Drucker H, Wu D, Vapnik N, et al. Support vector machines for spam categorization[J]. IEEE Transactions on Neural Networks, 1999, 11(5): 1048-1054.

[12] 于金龙, 李晓红, 孙立新. 连续属性值的整体离散化[J]. 哈尔滨工业大学学报, 2000, 32(3): 48-53.

YU Jinlong, LI Xiaohong, SUN Lixin. Global discretization of continuously valued attributes[J]. Journal of Harbin Institute of Technology, 2000, 32(3): 48-53.

[13] Nigam K, McCallum A, Thrun S, et al. Text classificat-ionfrom labeled and unlabeled documents using EM[J]. Machine Learning, 2000, 39(2): 103-133.

[14] SUN Xia, ZHANG Qingzhou, WANG Ziqiang. Using LPP and LS-SVM for spam filtering[C]// 2009 ISECS International Colloquium on Computing, Communication, Control, and Management. Washington: IEEE, 2009: 451-454.

[15] Cormack G, Lyman T. Spam corpus creation for feature[C]// Second Conference on Email and Anti-Spam CEAS2005. Stanford University, Palo Alto, 2005: 162-163.

(编辑  邓履翔)

收稿日期：2012-07-15；修回日期：2012-10-10

基金项目：国家自然科学基金资助项目(61272401, 61133005, 61173167, 61070194)；国家高技术研究发展计划(“973”计划)子项目(2012CB315801)

通信作者：杨金民(1967-)，男，湖南宁乡人，博士，教授，从事可靠计算、软件工程、数据挖掘研究；电话：13975896967；E-mail: rj_jmyang@hnu.edu.cn