基于Shannon熵噪声表征能力的系统状态辨识

张  雨^{1, 2}

(1. 南京工程学院 车辆工程系，江苏 南京，211167；

2. 东南大学交通学院，江苏 南京，210096)

摘  要：研究利用含噪程度差异辨识动力系统不同状态的可能性，采用符号时间序列的Shannon熵表征动力系统的含噪状态。由协方差矩阵最大特征值法或最小Shannon熵法获得符号序列长度L，得到符号序列直方图后便可计算Shannon熵。分别对不同瞬态工况的汽油汽车尾气HC排放、不同活塞环状态的柴油机机身振动、转子-定子不同碰摩状态的转子振动、汽车前悬架状态变化时的振动这4种动力系统计算Shannon熵，考察其对于系统含噪的表征能力和对于系统状态的辨识能力。研究结果表明：对于上述4种动力系统，Shannon熵都能指出含噪最强或最弱的那个状态，表明Shannon熵可用于辨识系统不同状态，但是，采用Shannon熵辨识系统状态的效能主要受状态之间含噪程度差异的影响。

关键词：信号处理；符号时间序列分析；Shannon熵；动力系统

中图分类号：O236；TK411⁺.5；TB533⁺.1；U461.1   文献标识码：A   文章编号：1672-7207(2008)06-1273-07

System condition identifying based on capacity of expressing noise with Shannon entropy

ZHANG Yu^{1, 2}

(1. Department of Vehicle Engineering, Nanjing Institute of Technology, Nanjing 211167, China;

2. College of Transportation, Southeast University, Nanjing 210096, China)

Abstract: The probability to identify the different conditions of dynamical system by using the difference of noise degree was studied. The Shannon entropy of symbolic time series was taken for the noise condition of dynamical system. After the length L of symbolic series was obtained by the method of covariance matrix maximal eigenvalue or the method of minimal Shannon entropy, the symbolic series histogram was gotten, and then the value of Shannon entropy was calculated. For the four kinds of dynamical systems, i.e., the gasoline vehicle HC tailpipe emission at different transient conditions, the diesel engine block vibration at different compressing ring conditions, the rotor vibration at different rub-impact conditions between rotor-stator, and the front suspension vibration at different automobile suspension conditions, the Shannon entropy was calculated, therefore the capability of Shannon entropy to character the system noise and to identify the system condition was reviewed. The results show that for the four kinds of dynamical system, the Shannon entropy can accord with the judge of mechanism analyses to distinguish the most strong or most weakly noise condition, which indicates the Shannon entropy can be used to identify the different system conditions. Meanwhile the efficiency to identify the system condition with the Shannon entropy is affected mostly by the difference of noise degree between the system conditions.

Key words: signal processing; symbolic time series analysis; Shannon entropy; dynamical system

系统信息的含噪状态可以采用多种方法描述。信息论认为，熵是衡量信息源在客观总体上的平均不确定性的量。熵越小，信息越确定，信息的无序程度越小^[1-2]。符号时间序列方法对时间序列施行符号化而得到“符号序列”，原来数值无穷变化的时间序列成为仅有几个数值(或符号)的符号序列。在这个“粗粒化”过程中，大尺度特征被留存，微弱的非重要信息被去除。由符号时间序列方法得到的符号熵，其描述的是符号序列的含噪状态，与由时间序列得到的熵相比，因为符号序列中仅留存着大尺度特征，故更能够表达系统信息的含噪状态，进而可用于对系统状态进行辨识。近年来，国内外许多学者采用符号熵^[3]或熵谱^[4]辨识隐藏在很强的观测噪声和动力学噪声中的确定性状态模式，如Finney等^[5-6]将符号熵用于研究火花点燃式发动机的循环可变性(Cycle variability)，并将符号熵用于发动机燃烧状态的测量与评估；Lin^[7]将符号熵用于检测和判断发动机失速的早期行为；Lehrman等^[8]将符号熵用于辨识混沌过程中不同变量之间的关   联度。

在此，本文作者考察采用符号熵的具体形式Shannon熵表征汽油机排放、活塞环胶结、转子碰摩、汽车悬架振动等几类动力系统含噪状态的能力，以此考察Shannon熵辨识动力系统状态的能力。将Shannon熵分别应用于以下4种动力系统的含噪表征和状态辨识：不同瞬态工况的汽油汽车尾气HC排放；不同活塞环状态的柴油机机身振动；转子-定子不同碰摩状态的转子振动；汽车前悬架状态变化时的振动。考察利用Shannon熵能够表征系统含噪状况的功能来辨识动力系统状态的能力。

1  含噪系统的熵描述

假设某系统具有n个信息源即x­₁, x₂, …, x_n，各信息源提供规定信息(类型、量值)的概率为p(x₁), p(x₂), …, p(x_n)，则该系统的信息结构为：

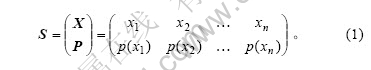
该系统的熵为：

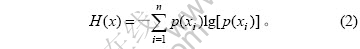
对于具有式(1)所示信息结构的系统，若同时还作用了m个噪声干扰源n₁, n₂, …, n_m，各噪声干扰源出现的概率为p(n₁), p(n₂), …, p(n_m)，则该含噪系统的信息结构为：

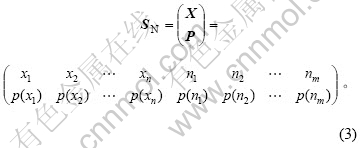
该具有n个信息源和m个噪声源的含噪系统的熵为：

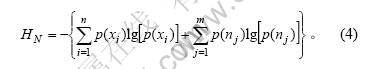
与式(2)相比，含噪系统出现了熵增，即H_N(x)≥H(x)，系统信息的无序程度增加，因此，可以用熵表征系统的含噪状态。

导致系统含噪的原因是多方面的，其中有以下5个主要原因：系统运行时受到动力学噪声的干扰；获取信息的检测系统不可避免地带噪并受到环境噪声污染；因截取信号等价于加窗而导致信息泄漏；被检测信息自身的数学特征与所采用辨识方法的数学前提不很匹配而衍生出的新噪声；几乎所有信号处理方法都不可能从根本上完全消除噪声的影响。对于具有非平稳性、时变性、非线性和模糊性的动力系统，这5个主要原因的影响效果更加不容忽视。

根据大数定理和中心极限定理，若系统受到影响显著的因素作用，则系统的正态特性被破坏，系统信息的无序程度降低，系统出现熵减。在设备状态监测与故障诊断工作中，这是判断被监测系统是否处于显著破坏状态的一个方法。

2  符号时间序列分析及其统计量

2.1  时间序列符号化简介

符号时间序列分析^[9]是通过在几个可能值上离散时间序列而形成新的符号序列。引入划分P={P₁, P₂, …, P_q}，并把系统状态空间划分为m=(q+1)^d个单元。其中：d为状态空间的维数；q为划分个数，q=1为最简单的二进制划分。每个单元用1个符号S_r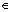{S₁, S₂, …, S_m}进行标记。在相空间为连续曲线的系统轨迹将被转换为符号序列，这些符号标记了被轨迹所访问的单元。

可以通过一个阈值函数，将时间序列{x_n}的元素转换为符号序列{s_n}的元素：

在确定了符号序列长度(树层数)L和时延后，可把符号序列{s_n}分组为短序列：

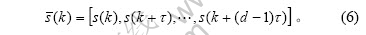
2.2  确定符号序列长度L的方法

在一般情况下，符号序列长度L可以由协方差矩阵最大特征值法或最小Shannon熵法获得。

协方差矩阵最大特征值法的原理是：向量集{X_j}包括原时间序列中的全部元素。故根据嵌入理论可知，向量集{X_j}构成的状态轨道保留了原空间状态轨道的一些主要特征。由向量集{X_j}构造如下轨道矩阵X：

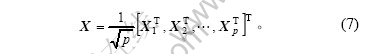
对X构造协方差矩阵S=X^TX，通过满秩线性变换使其成为标准型。当相空间维数由小到大变化而协方差矩阵S的最大特征值不随其变化时，则选定最小嵌入相空间维数，也就获得了符号序列长度L。

最小Shannon熵法的原理是：Shannon熵H_s(L)随符号序列长度L的变化而变化。令L从1开始增加，当H_s(L)达最小值时，符号化变换可以较好地区分动力学数据与随机噪声，也就选定了符号序列长度L。

2.3  Shannon熵—— 度量系统信息无序程度的统计量

将时间序列转换为符号序列并经十进制编码后，可获得符号时间序列直方图。其中确定性信号对应的序列码呈现大概率，随机噪声对应的序列码则呈现等概率，这一特性可用于检测未知原始时间序列中是否包含有确定性结构。

由符号时间序列直方图可得到统计量——Shannon熵。在二进制划分下，可定义Shannon熵为：

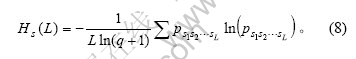
Shannon熵可描述数据紊乱的程度。对于混沌或随机数据，其Shannon熵趋向于1；对于确定性数据，其Shannon熵趋向于0。Shannon熵给出了动力学系统时间序列信息的宏观外部随机性，即外随机程度。因此，可采用Shannon熵评价系统的含噪状态。通过对Shannon熵的比较，可以判断不同时间序列之间确定性程度的差异，故Shannon熵可用于区分不同动力系统的差别，这是考虑Shannon熵能否被用于辨识动力系统不同状态的基本前提。

3  系统信息含噪的Shannon熵表征及其工程应用

3.1  汽油汽车尾气HC瞬态排放状态的辨识

对于满足欧Ⅱ排放法规的某雪铁龙汽油汽车，分别在冷起动(汽车静置24 h后1次启动成功)、暖机(紧接冷起动后进行)、加速-滑行(在底盘测功机上进行)3种瞬态工况下，检测尾气中HC的排放量^[10]。图1(a)所示为在3种瞬态工况下尾气HC排放的时间序列，信号采样频率为0.72 Hz。在进行动态信号采集时，选择A/D变换器的采样频率应在分析信号结构的基础上遵循采样定理并予以确定。对其采用二进制符号化规则得到符号序列，继而可作出符号时间序列直方图并计算其Shannon熵，如图1(b)所示。

由机理分析结果可知^[11]，在汽油汽车在冷启动和暖机状态时，汽油机转速较低使得进气流速较小及进气量较小，导致混合气的湍流程度和均匀程度较低；汽油机气缸壁温度和压缩终了混合气的温度较低，导致燃料汽化与着火性能较差。最终使冷起动和暖机状态时汽油机的燃烧状态较差，热力性能不稳定，尾气流脉动的随机紊乱程度加剧，HC排放量较大，表现在此时Shannon熵应大于加速-滑行时的Shannon熵。图1(b)中不同瞬态工况下HC排放的Shannon熵反映了上述机理分析结果：冷起动和暖机工况下HC排放的Shannon熵相同，均为0.68；加速-滑行工况下HC排放的Shannon熵较小，为0.61。表明冷起动和暖机工况的HC排放其随机紊乱程度较大，变化规律较复杂，排放量较大；而加速-滑行工况的HC排放其含噪程度下降，数据结构的确定性较强，排放量较小。因此，Shannon熵区分了冷起动/暖机与加速-滑行2类不同瞬态工况下的排放状态，直方图也反映了同样的结果。

3.2  柴油机活塞环胶结状态的辨识

图2(a)所示为某4135G柴油机第4缸在3种活塞环状态时的机身振动加速度时间序列，试验工况如下：75%负荷，转速为1 500 r/min，信号采样频率为6.4 kHz。该机型具有3道活塞环。其中，1g=9.8 m/s²。直接由图2(a)所示的机身振动时间序列信号辨识不同活塞环状态很困难。由图2(a)可得到符号序列，对其作出符号时间序列直方图后可计算Shannon熵，如图2(b)所示。

可以证明^[12]：对于具有3道活塞环(气环)的柴油机燃烧室，当第Ⅰ道活塞环发生胶结时，由于其迷宫密封作用丧失，作用在第Ⅱ和第Ⅲ道活塞环上的激励力增强，使得活塞环的径向振动有所加强，故此时振动数据的确定性加强，机身振动时间序列的含噪程度下降，数据结构的确定性较强；而当第Ⅰ和第Ⅱ道活塞环都发生胶结时，由于这2道环的迷宫密封作用丧失，导致气体力减小，继而使得活塞环振动减小，故机身振动时间序列数据结构的确定性减弱。

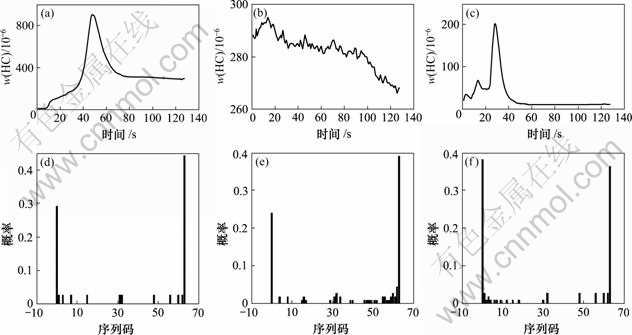
时间序列信号：(a) 冷起动；(b) 暖机；(c) 加速-滑行 符号时间序列直方图和Shannon熵：(d) 冷起动(熵为0.68)；(e) 暖机(熵为0.68)；(f) 加速-滑行(熵为0.61)

图1  某雪铁龙RPC汽油汽车尾气中HC成分时间序列及其Shannon熵

Fig.1  Tailpipe emission HC time series and its Shannon entropy of a Citroen gasoline vehicle

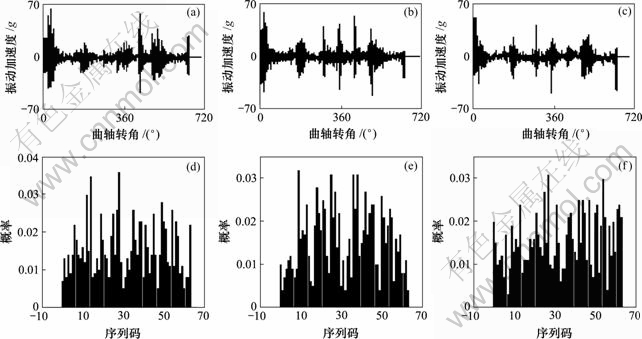
时间序列信号：(a) 正常；(b) 第Ⅰ道活塞环胶结；(c) 第Ⅰ和第Ⅱ道活塞环胶结 符号时间序列直方图和Shannon熵：(d) 正常(熵为0.98)；(e) 第Ⅰ道活塞环胶结(熵为0.97)；

(f) 第Ⅰ和Ⅱ道活塞环胶结(熵为0.98)

图2  某4135 G柴油机第4缸机身振动加速度时间序列及其Shannon熵

Fig.2  Black vibration acceleration time series and its Shannon entropy of a 4135G diesel engine 4th cylinder

图2(b)中不同活塞环状态的Shannon熵反映了这一结果：当第Ⅰ道活塞环胶结时，Shannon熵有最小值，据此可辨识柴油机第Ⅰ道活塞环出现了胶结。

3.3  辨识转子-定子碰摩状态

图3(a)所示是某转子-定子处于3种碰摩状态时的转子振动位移平面轨迹时间序列，试验工况为：空负荷，转速为3 240 r/min，信号采样频率为200 Hz。由图3(a)可得到符号序列，对其作出符号时间序列直方图后可计算Shannon熵，如图3(b)所示。

根据机理分析，在转子-定子碰摩瞬间，转子系统的固有频率提高，转子频率在提高了转子系统固有频率的某分频范围内，出现了分频或混沌状态^[13]，此时，转子振动位移信号含噪程度增强，数据结构的确定性减弱。这种状态的产生与改变是与转  子-定子之间的接触刚度即碰摩状态密切相关，宏观上表现为与转子-定子接触的尖锐程度密切相关。Shannon熵是数据紊乱程度的度量，故在分频或混沌状态下Shannon熵应比确定性状态下的Shannon熵高。图3(b)中转子-定子处于早期尖锐型碰摩时的Shannon熵为0.76，大于其他2种工况的Shannon熵，证明了上述分析结果。以此为准则可以判断转子-定子是否处于早期尖锐型碰摩状态。

3.4  辨识汽车前悬架状态

选择具有钢板弹簧式非独立前悬架的某BJ212汽车，利用制动时车辆轴载的冲击性转移激发悬架振动的原理^[14-15]，采用4PLD型汽车制动-悬架隔振效率实验台，在前悬架分别为6片(原始状态)、4片、2片钢板弹簧的工况下，当车速为5 km/h时获得汽车制动过程中的前悬架振动时间序列，信号采样频率为50 Hz。对其采用二进制符号化规则得到符号序列，继而可作出符号时间序列直方图并计算其Shannon熵，如图4(b)所示。注意到在4片钢板弹簧工况下前悬架振动的Shannon熵小于其他2种工况的熵，此时，前悬架振动信号的含噪程度最弱，数据结构的确定性最强。

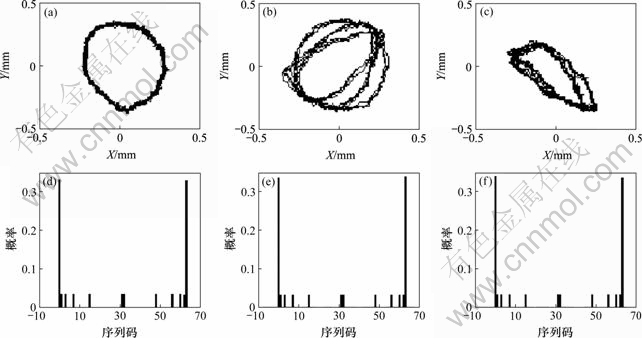
时间序列信号：(a) 正常；(b) 早期尖锐型碰摩；(c) 晚期平钝型碰摩符号时间序列直方图和Shannon熵：(d) 正常(熵为0.74)；(2) 早期尖锐型碰摩(熵为0.76)；(3) 晚期平钝型碰摩(熵为0.74)

图3  某转子振动位移信号平面轨迹及其Shannon熵

Fig.3  Vibration displacement signal and its Shannon entropy of a rotor

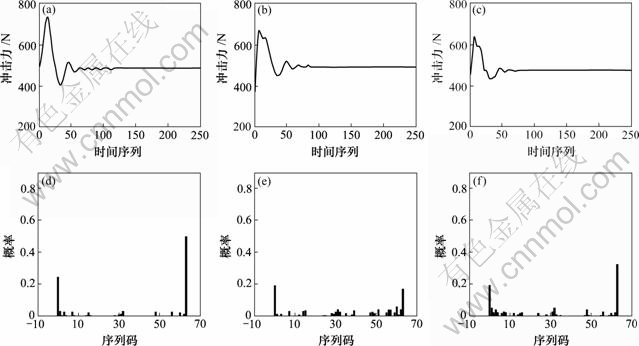
时间序列信号：(a) 6片钢板弹簧；(b) 4片钢板弹簧；(c) 2片钢板弹簧符号时间序列直方图：(d) 6片钢板弹簧(熵为0.29)；(e) 4片钢板弹簧(熵为0.25)；(f) 2片钢板弹簧(熵为0.32)

图4  某BJ212汽车前悬架振动时间序列及其Shannon熵

Fig.4  Front suspension vibration time series and its Shannon entropy of a BJ212 vehicle

通过分析可知^[16]，对于具有钢板弹簧式非独立前悬架的汽车，当前悬架钢板弹簧数量开始减少时，悬架吸收振动冲击的能力下降，悬架的减振能力下降，悬架振动的“复杂程度”减弱；而当前悬架钢板弹簧数量进一步减少时，前悬架基本丧失了减振隔振能力，路面激励引起的车辆振动更多地未被悬架吸收衰减而直接传递作用于车架，悬架-车架之间的相互激励使得悬架振动的“复杂程度”增加。因而，当4片钢板弹簧时悬架振动的Shannon熵有最小值，而2片钢板弹簧时悬架振动的Shannon熵有最大值。这可以采用Shannon熵辨识汽车钢板弹簧式非独立前悬架的状态，当悬架因钢板弹簧缺失、失效、松旷时予以确认。

4  结  论

a. 含噪系统出现熵增。反映符号序列总体特征的统计量Shannon熵直接描述了系统信息含噪的程度。通过对Shannon熵的比较，可以判断不同时间序列之间确定性程度的差异，因此，Shannon熵可用于区分不同动力系统含噪的差别，因而间接地用于辨识动力系统的状态。

b. 符号序列长度L可以由协方差矩阵最大特征值法或最小Shannon熵法获得：当Shannon熵H_s(L)有最小值时的符号序列长度L为最佳值；当协方差矩阵的最大特征值不随相空间维数变化而变化时的最小嵌入相空间维数等于符号序列长度L。由上述2种方法之一可确定合适的符号序列长度L，并作出符号序列直方图，可计算出此时的符号熵即Shannon熵。

c. 分别对不同瞬态工况的汽油汽车尾气HC排放、不同活塞环状态的柴油机机身振动、转子-定子不同碰摩状态的转子振动、汽车前悬架状态变化时的振动这4类动力系统计算Shannon熵，考察其对于动力系统含噪的表征能力和对于系统状态的辨识能力。结果表明，对于这几类动力系统， Shannon熵计算结果都能够符合机理分析的判断，反映含噪最强的那个状态，这说明Shannon熵可用于辨识系统不同状态。但是，需注意的是，采用Shannon熵辨识系统状态的效能主要受状态之间含噪程度差异的影响。

参考文献：

[1] 王雨田. 控制论·信息论·系统科学与哲学[M]. 北京: 中国人民大学出版社, 1986.
WANG Yu-tian. Cybernetics, information theory, system science and philosophy[M]. Beijing: Press of People’s University of China, 1986.

[2] 王书方. 关于自然信息的哲学思考[J]. 中南大学学报: 社会科学版, 2007, 13(3): 258-261.
WANG Shu-fang. The principle on philosophy of science about nature information[J]. Journal of Central South University: Social Science Edition, 2007, 13(3): 258-261.

[3] Crutchfield J P, Packard N H. Symbolic dynamics of noisy chaos[J]. Physica D, 1983(7): 201-223.

[4] 姚 屏,申群太, 王俊年. 语音信号的谱熵检测在车辆通信中的应用[J]. 中南大学学报: 自然科学版, 2005, 36(5): 858-862.
YAO Ping, SHEN Qun-tai, WANG Jun-nian. Application of voice detection to vehicle communication based on spectral entropy[J]. Journal of Central South University: Science and Technology, 2005, 36(5): 858-862.

[5] Finney C E A, Green J B, Daw C S. Symbolic time series analysis of engine combustion measurements[J]. SAE, 1998(6): 251-273.

[6] Finney C E A, Nguyen K, Daw C S, et al. Symbol statistics for monitoring fluidization[C]//ASME. Proceeding of International Mechanical Engineering Congress and Exposition. California: Anaheim Publisher, 1998: 223-230.

[7] LIN Feng. Use of symbolic time series analysis for stall precursor detection[J]. Journal of AIAA, 1998(10): 3310-3316.

[8] Lehrman M, Rechester A B, White R B. Symbolic analysis of chaotic signals and turbulent fluctuations[J]. Physical Review Letters, 1997, 78(1): 54-57.

[9] 张 雨. 符号化时间序列分析[J]. 湘潭矿业学院学报, 2004, 19(1): 75-79.
ZHANG Yu. Symbolic time series analysis[J]. Journal of Xiangtan Mining Institute, 2004, 19(1): 75-79.

[10] 张 雨, 刘少伦. 汽油机瞬态排放检测的新实践[J]. 小型内燃机与摩托车, 2004, 33(6): 28-30.
ZHANG Yu, LIU Shao-lun. The practices on detection of transient exhaust of gasoline engine[J]. Small Internal Combustion Engine and Motorcycle, 2004, 33(6): 28-30.

[11] 张 雨. 汽油机瞬态排放分析[M]. 长沙: 国防科技大学出版社, 2005.
ZHANG Yu. The analyses on transient exhaust of gasoline engine[M]. Changsha: National University of Defense Technology Press, 2005.

[12] 张 雨, 张志沛, 周轶尘. 内燃机主运动副振动监测技术的研究[M]. 北京: 中国铁道出版社, 1998.
ZHANG Yu, ZHANG Zhi-pei, ZHOU Yi-chen. The research on technology of vibration monitoring for main moving assembly of internal combustion engine[M]. Beijing: China Railway Press, 1998.

[13] 胡茑庆, 张 雨, 刘耀宗, 等. 转子系统动静件间尖锐碰摩时的振动特征试验研究[J]. 中国机械工程, 2002, 13(9): 777-780.
HU Niao-qing, ZHANG Yu, LIU Yao-zong, et al. Experimental research on vibration characteristics of sharp rub-impact between rotor and stator of a rotor system[J]. China Mechanical Engineering, 2002, 13(9): 777-780.

[14] JT/T 488—2001, 汽车悬架装置检测台技术条件[S].
JT/T 488—2001, The techno-condition on inspecting rig for vehicle suspension set[S].

[15] Decker H, Schramn W, Bethell M R. An optimized approach to suspension control[J]. SAE, 1990(6): 1010-1020.

[16] ZHANG Yu, REN Cheng-long. Test analysis on relationship between anti-vibration performance and chaos characteristics of vehicle suspension[J]. Journal of Southeast University, 2006, 22(1): 64-68.

收稿日期：2008-01-06；修回日期：2008-03-05

基金项目：江苏省“六大人才高峰”项目(07-D-014)；江苏省高校自然科学基础研究项目(07KJD580084)；南京工程学院科研基金资助项目(科07-106)

通信作者：张  雨(1958-)，男，江苏泰州人，博士后，教授，从事汽车检测理论与状态智能监测研究；电话：025-86118978；E-mail: zy586187@163.com