文章编号: 1004-0609(2006)10-1684-05
近片层γ-TiAl基合金宏观塑性行为的尺度效应
苏继龙1, 胡更开2
(1. 福建农林大学 机电工程学院, 福州 350002; 2. 北京理工大学 应用力学系, 北京 100081)
摘 要: 将近片层γ-TiAl基合金视为由等轴γ颗粒和多孪晶PST(polysynthetically twinned crystal)单晶颗粒组成的两相复合材料。 基于非均质微极介质塑性理论, 构建γ-TiAl基合金整体有效微极柔度张量, 将传统塑性割线模量法推广到微极材料, 建立分析和预测γ-TiAl基合金的塑性行为尺度效应的细观力学模型。 结果表明: γ-TiAl基合金的微结构尺度对其宏观塑性硬化行为存在显著的影响; 近片层组织γ-TiAl基合金中PST晶体颗粒的尺寸越小, 合金中硬相夹杂PST颗粒的体积分数越大, 合金材料相应的塑性硬化越明显; 微极基体的塑性特征尺度与等轴γ晶粒的平均尺寸大小在同一数量级。
关键词: γ-TiAl基合金; 塑性; 微极理论; 尺度效应; 细观力学
中图分类号: TH142.2 文献标识码: A
Effect of grain size on macroscopic plastic behavior of nearly lamellar γ-TiAl-based alloys
SU Ji-long1, HU Geng-kai2
(1. College of Mechanics-Electrics Engineering,
Fujian Agriculture and Forestry University, Fuzhou 350002, China;
2. Department of Applied Mechanics,
Beijing Institute of Technology, Beijing 100081, China)
Abstract: An analytical micromechanical model in a framework of a micropolar continuum was proposed to investigate the size effect of macroscopic plastic behavior for a nearly lamellar γ-TiAl based alloy, which consisted of PST(polysynthetically twinned crystal) grains with random orientation. The γ-TiAl based alloy was considered as a two-phase composite composed of micropolar matrix and PST particles. The Mori-Tanaka's method was advanced to evaluate the effective elastic moduli, and a new secant moduli method based on the second moment of strain and torsion of the matrix was extended to analyze the nonlinear behaviour of the γ-TiAl based alloy. The modeling results show that the size dependence is more pronounced when the PST particles size approaches to the matrix characteristic length. The plastic stress of a nearly lamellar γ-TiAl based alloy increases with the decrease of PST grain size or with the increasing volume fraction of the PST grains. The characteristic length of plasticity of the micropolar matrix is approximately as the same order of magnitude as the average diameter of the matrix particles.
Key words: γ-TiAl-based alloys; plasticity; micropolar theory; size effect; micromechanics
γ-TiAl基合金被认为是非常有前途的新型轻量化高温结构材料, 在航空、 航天、 汽车等领域具有广阔的应用前景。 由于其可控的多种微结构组织 形式和良好的高温结构强度, 近年来, 两相(γ-TiAl+α2-Ti3Al)γ-TiAl基合金一直是倍受关注的高温结构材料[1-5]。 弹、 塑性性能以及变形、 断裂及韧化机制一直是γ-TiAl基合金宏观力学性能的研究重点。 目前主要集中于制备工艺及力学性能测试, 对其弹、 塑性及断裂和蠕变性能及发生机理的定量研究也基本上是采用有限元数值方法; 而对其弹、 塑性及断裂和蠕变行为进行细观力学建模, 尤其是对γ-TiAl基合金产品的宏观性能与其微结构尺度之间的关系还缺乏系统的研究[6]。 对于γ-TiAl基合金, 其组织中包含具有复杂微结构的由γ和α2片层所构成的多孪晶PST(polysynthetically twinned crystal)颗粒, 因此, 存在对其微结构尺度进行描述的问题[3, 7]。 当合金中的等轴γ颗粒和多孪晶PST单晶颗粒进一步细化时, 探讨合金组分的尺度以及材料的非均质性对其宏观力学性能的影响尤为重要。 针对γ-TiAl基合金的塑性尺度效应已有一些实验结果[8, 9], 但没有建立相应的塑性行为尺度效应的定量分析预测模型, 其主要原因是, 描述传统材料的塑性变形理论因不涉及尺寸因素, 从而不能预测塑性硬化行为的微结构尺度效应。 而最近发展起来的微极介质理论适用于材料的微结构效应不可忽略的情况[10-13], 当具有两相组分的合金材料中夹杂颗粒尺度与基体微结构特征尺度相当时, 夹杂的尺度对材料宏观力学性能产生显著的影响。 近片层γ-TiAl基合金由等轴γ晶粒和体积分数较大的多孪晶PST单晶颗粒组成, 它是γ-TiAl基合金4种典型的组织形式之一[1, 3]。 本文作者将其视为由等轴γ颗粒和多孪晶PST单晶颗粒所构成的两相复合材料, 运用微极细观力学理论, 在考虑此合金组织中PST颗粒的横观各向同性及空间取向任意分布的前提下, 首先是构建近片层γ-TiAl基合金有效微极弹性柔度张量, 进而推导了割线模量, 在此基础上, 将分析传统材料塑性的割线模量法推广到具有微极特性的复合材料塑性行为的分析中, 建立预测近片层γ-TiAl基合金塑性硬化行为尺度效应的细观力学模型, 模拟其单轴拉伸应力—应变响应, 并与已有的实验结果进行比较。
1 微极复合材料塑性割线模量法
微极(micropolar)理论[12]假定材料介质中任一微元体的运动不仅具有经典的3个位移自由度, 还有3个独立的旋转自由度, 结果是非均质材料介质中的每一点不仅能承受常规意义上的应力, 而且可以承受偶应力。 微极理论能够描述传统连续介质理论不能描述的微结构尺度对材料宏观性能的影响, 因为与旋转位移有关的由应力产生的力矩与应力的大小、 方向及力点的位置有关, 从而引入了尺度量。 复合材料的塑性行为, 即应力应变关系与材料的微结构、 加载方式等因素有关。 为了对γ-TiAl基合金进行宏观有效塑性行为的分析, 首先将传统Cauchy介质的J2全量理论推广到微极介质塑性分析中, 建立外载作用下微极基体中类似von-Mises应力的有效应力的计算公式; 结合材料中PST颗粒的横观各向同性及取向任意的分析, 得到微极介质基体的割线模量; 在此基础上再运用类似传统Cauchy介质的割线模量法通过迭代计算得到γ-TiAl基合金的应力应变关系, 进而预测其塑性行为的尺度效应。 该方法的核心是如何表征外载作用下的发生塑性变形的基体中的有效应力, 根据Lippmann[14]理论, 类似传统介质等效von-Mises应力的定义方法, 微极介质基体的有效应力可定义为
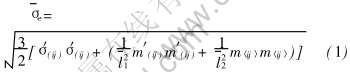
式中 σ′(ij)为应力对称部分的偏量, 而m′(ij)和m〈ij〉为微极偶应力的对称部分的偏量及偶应力的反对称部分。 当忽略微极效应, 即上式中所有m量为零, 则等效应力退化成传统Cauchy介质的von-Mises等效应力。 其中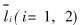 
是材料在塑性状态下的内在尺度参数, 称为材料的塑性特征尺度, 与基体材料的微结构尺寸有关, 不失一般性, 本文中取值为 
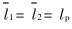。 上述等效应力的定义意味着应力的球量部分、 反对称部分和偶应力的球量部分不参与材料的塑性变形。
对于传统Cauchy介质, HU[15]发展了非均质材料细观塑性二阶矩方法, 该方法克服了一阶矩割线模量存在的缺陷。 下面将塑性二阶矩方法推广到由微极介质构成的复合材料中。
对于复合材料, 根据实际破坏形式, 一般认为在外载作用下硬相夹杂保持弹性, 而当其基体发生屈服时即认为复合材料整体屈服。 因此, 讨论基体屈服的关键就是要确定基体中的等效应力, 而对于基体中的复杂应力状态, 其应力和力偶不是均匀的, 只能在平均意义下给出基体的平均等效应力。 下面将给出基体内平均等效应力的计算方法。 首先将宏细观能量等价式:
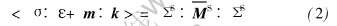
改写成柔度形式
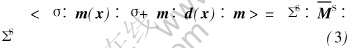
式中 σ和m分别为应力和偶应力张量; ε和k分别表示应变和扭率张量; d为微极理论中的弹性系数张量; ΣS为外载荷;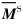 
为复合材料的有效柔度张量; 上标S表示各量对应的是传统均匀对称外载应力场, 而〈·>表示在代表单元内平均。
对代表单元保持外载荷不变, 让局部材料柔度张量产生如下独立变分δm(x), δd(x), 这样宏观柔度张量也将产生变分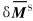
, 这样式(3)最终化为
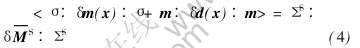
因此由式(1)定义的微极基体中的平均等效应力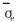 
最终可表达为
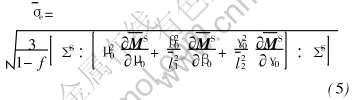
可以看出, 基体中平均等效应力与外载荷ΣS及复合材料整体的柔度张量M[TX-]S有关。 值得注意的是, 对于本文中所讨论的近片层γ-TiAl基合金材料, 作为增强相的PST颗粒不是各向同性的, 而是横观各向同性, 从而导致在微极理论框架下求解合金的有效柔度张量 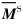比较复杂, 要涉及到合金中PST颗粒的横观各向同性及取向任意分布的处理。 本文作者将合金中等轴γ颗粒视为微极基体, 同时考虑到对微极介质目前只有球形和无限长圆柱形夹杂有相应的解析类Eshelby张量, 故PST晶体颗粒被视为有空间取向的球形夹杂(直径为a), 在微极理论框架下推广Mori-Tanaka法并结合空间角度平均, 求得近片层γ-TiAl基合金的有效柔度张量 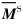。 同时应注意到, 材料的微结构尺度信息, 包括基体材料的塑性特征尺度 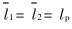是通过柔度张量 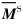体现出来的。 这样, 令平均等效应力 
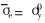, 即可确定复合材料的屈服面, 这里σ0y为微极基体的初始屈服应力。 而整个复合材料的塑性硬化行为可按照Cauchy介质的割线模量方法来加以描述。 割线模量方法的核心是假设有一线性比较材料, 该材料的基体是由割线模量决定。 根据塑性全量理论, 微极基体产生塑性变形后的割线模量的分量元素可定义为
式中 μ为传统材料的Lame常数; κ, γ, β为微极理论中新引入的材料弹性常数; K为材料体积模量; L为与K相对应的偶应力关系的量; H, n和σy为材料的硬化参数。 当外载荷使得基体的平均等效应力满足 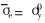时, 复合材料开始屈服。 在给定任意外载荷ΣS(复合材料已经开始屈服)时, 用线性比较复合材料来描述非线性复合材料此时的应力与应变关系。 该线性比较复合材料具有与所研究的复合材料相同的微观结构, 其基体具有非线性复合材料基体的平均割线模量。
线性比较复合材料的弹性柔度张量 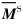就是非线性复合材料在当前应力下的割线柔度张量, 通过式(5)、 (6)及线性比较复合材料的模量关系式, 可以确定在给定对称外载
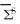作用下对应复合材料的应变为
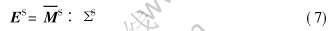
于是非线性合金材料的应力—应变关系, 也即塑性硬化曲线就可以通过一系列线性比较复合材料的弹性模量得到。 当不考虑基体的极性时(或夹杂颗粒尺度远大于基体的塑性特征尺度), 上述方法退化为传统Cauchy介质的塑性割线模量法。
2 近片层γ-TiAl基合金的塑性应力应变关系
运用前面介绍的在微极理论框架下推广的塑性割线模量法来预测近片层γ-TiAl合金的塑性硬化行为, 以等轴γ颗粒为微极基体, 硬相PST颗粒为夹杂, 重点考察微结构尺度对材料等效应力应变关系的影响。 假设在无穷远处有一单轴拉伸载荷作用在合金上, 夹杂一直处于弹性状态, 基体屈服。 对屈服基体, 将传统材料的幂硬化关系推广到微极介质材料, 即有
式中 σy, H, n材料的硬化参数, 可由单向拉伸实验结果获得。
在微极理论框架下, 结合Mori-Tanaka方法, 先计算出γ-TiAl合金整体平均有效弹性模量和割线模量, 再进行塑性硬化分析。 计算过程中PST多晶体颗粒弹性常数可由PST单晶体弹性性质通过空间平均得到: E=185.656GPa, v=0.2543; 而等轴γ颗粒微极基体的弹性常数为: E=140GPa, v=0.296; 其相应的微极介质弹性参数选取为: κ0=μ0, α0=l2mμ0, β0=l2mμ0, γ0=l2mμ0, 其中lm为基体微极介质的弹性特征尺度, 它与塑性特征尺度lp的关系可设为lp=2lm。 计算中基体材料的幂硬化关系材料常数选取为: σy=230.5MPa, H=175.0MPa, n=0.454。
图1给出了γ-TiAl基合金材料中夹杂PST颗粒体积分数为f=0.90, PST单晶颗粒中α2相体积分数为fr=0.10, 而基体材料塑性特征尺度取lp=2lm=20μm, PST颗粒直径分别为a=10μm, 75μm, 200μm和500μm, 即分别为基体材料特征尺度lm的1倍, 7.5倍和20倍及50倍时的近片层γ-TiAl基合金拉伸塑性行为的应力应变关系曲线。 将Kim[9]的实验结果同时放在图1中进行比较, 实验所用的近片层γ-TiAl基合金的两相组分尺寸是等轴γ颗粒平均大小为20μm, PST颗粒平均大小为108μm, 而PST颗粒体积分数为f=0.90。 由图1可知, 基于微极理论对近片层γ-TiAl合金宏观塑性硬化行为的预测趋势与实验结果相吻合, 更重要的是基于微极理论的塑性预测模型能够很好地反映出近片层γ-TiAl基合金的塑性硬化的尺度效应。 在合金夹杂相体积分数和基体塑性特征尺度一定的情况下, PST夹杂颗粒的尺寸越小, 合金材料对应发生相同应变时的应力越大, 即表现出明显的硬化趋势, 而传统的细观力学方法无法预测这种变化。 在图1中还可以发现, 当PST夹杂颗粒尺度远大于基体特征尺度时(如a=50lm), 预测结果退化为不考虑基体微极效应所对应的传统结果, 此时两条曲线相重合。 另外, 图1中取微极基体塑性特征尺度参数lp=20μm, 此时PST颗粒a=75μm时的应力预测结果比实验所用的等轴γ基体颗粒尺度为20μm, 夹杂PST颗粒直径a=108μm材料的应力稍大, 与尺度效应影响趋势完全一致, 这也说明了微极基体的塑性特征尺度与基体微结构的平均尺寸大小是同一数量级。
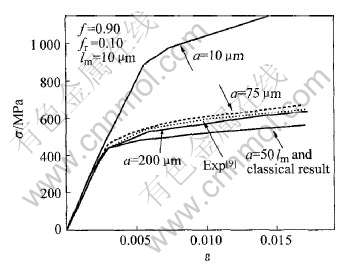
图1 γ-TiAl基合金PST夹杂尺度对合金应力—应变曲线的影响
Fig.1 Effects of particle size of PST on effective stress—strain curves
保持基体塑性特征尺度和夹杂PST颗粒尺寸a=75μm不变, 合金材料应力应变关系曲线随PST夹杂颗粒的体积分数f变化的趋势如图2所示, 其中的实验数据同图1所示。 由图可知: 夹杂PST颗粒体积分数越大, 合金塑性硬化也越明显。
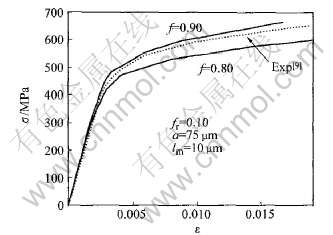
图2 PST颗粒体积分数f对合金硬化曲线的影响
Fig.2 Effects of volume fraction of PST on effective stress—strain curves
3 结论
1) 将近片层γ-TiAl基合金视为由等轴γ颗粒和PST晶体颗粒两相所组成的复合材料, 运用细观力学方法可建立其宏观塑性行为尺度效应的预测模型。
2) 在考虑夹杂相PST颗粒的横观各向同性和空间任意分布的前提下, 给出了近片层γ-TiAl基合金有效弹性模量和基于微极基体的割线模量的计算方法。
3) 当近片层γ-TiAl基合金中PST颗粒夹杂的体积分数和微极基体塑性尺度一定时, PST颗粒的尺寸越小, 对应同一应变时合金的应力越大, 即塑性硬化越明显; PST夹杂颗粒体积分数、 微极基体塑性特征尺度等因素对近片层γ-TiAl合金的塑性行为均有影响, 微极基体的塑性特征尺度与等轴γ晶粒的平均尺寸大小是同一数量级。
REFERENCES
[1]Appel F, Wagner R. Microstructure and deformation of two-phase titanium aluminides[J]. Mater Sci Eng A, 1998, 22(5): 187-268.
[2]Kim Y W. Ordered intermetallic alloys, part Ⅲ: Gamma titanium aluminides[J]. Journal of Metall, 1994, 46(7): 30-39.
[3]Dimiduk D M, Hazzledine P M, Parthasarathy T A, et al. The role of grain size and selected microstructure parameters in strengthening fully lamellar TiAl alloys[J]. Metall Mater Trans A, 1998, A29(1): 37-47.
[4]彭超群, 黄伯云. TiAl基合金在快速加热循环热处理过程中的结构失稳[J]. 稀有金属材料与工程, 2004, 33(4): 363-367.
PENG Chao-qun; HUANG Bai-yun. Microstructural instability of a TiAl-based alloy during rapid heating cyclic heat treatment[J]. Rare Metal Materials and Engineering, 2004, 33(4): 363-367.
[5]郑瑞廷, 郭富安, 张永刚, 等. 双态组织TiAl基合金拉伸塑性的断裂力学[J].中国有色金属学报, 2001, 11(2): 114-118.
ZHENG Rui-ting, GUO Fu-an, ZHANG Yong-gang, et al. Fracture mechanics of tensile ductility of TiAl alloy with duplex structure[J].The Chinese Journal of Nonferrous Metal, 2001, 11(2): 114-118.
[6]Dimiduk D M, Parthasarathy T A. Hazzledine P M. Design-tool representations of strain compatibility and stress-strain relationships for lamellar gamma titanium aluminides[J]. Intermetallics, 2001, 9(10): 875-882.
[7]Fischer F D, Appel F, Clemens H. A thermodynamical model for the nucleation of mechanical twins in TiAl[J]. Acta Materialia, 2003, 51(5): 1249-1260.
[8]Kim Y W. Strength and ductility in TiAl alloys[J]. Intermetallics, 1998, 6: 623-628.
[9]Kim Y W. Microstructural evolution and mechanical properties of a forged gamma titanium aluminide alloy[J]. Acta Metall Mater, 1992, 40(6): 1121-1134.
[10]Eringen A C. Theory of Micropolar Elasticity in Fracture Mechanics[M]. (Vol Ⅱ). New York: Academic Press, 1968: 621-729.
[11]Mindlin R. Microstructure in linear elasticity[J]. Arch Rat Mech Anal, 1964, 16(1): 51-78.
[12]Eringen A C. Microcontinuum field theory[M]. New York: Springer Press, 1999.
[13]German P. La methode des puissances virtuelles en mecanique des milieux continues premiere partie: theorie du second gradient[J]. Journal de Mecanique, 1973, 12: 235-274.
[14]Lippmann H. Cosserat plasticity and plastic apin[J]. Asme Appl Mech Rev, 1995, 48: 753-762.
[15]HU Geng-kai. A method of plasticity for general aligned spheroidal void or fiber-reinforced composites[J]. International Journal of Plasticity, 1996, 12(4): 439-449.
[16]Dimiduk D M. Gamma titanium aluminide alloys-an assessment within the competition of aerospace structure materials[J]. Mater Sci Eng A, 1999, A263: 281-288 .
(编辑李向群)
基金项目: 国家自然科学基金资助项目(10325210)
收稿日期: 2006-04-29; 修订日期: 2006-09-19
通讯作者: 苏继龙, 博士; 电话: 0591-83789374; E-mail: fjsu@163.com
