棒材热轧过程的三维温度场有限元分析
向 勇，谭建平
(中南大学 机电工程学院，湖南 长沙，410083)
摘 要：基于有限元分析软件MARC，采用更新的Lagrange法描述的热力耦合大变形弹塑性有限元模型和四面体等参单元技术，考虑接触界面传热，对棒材热轧成形工序进行了三维温度场模拟。模拟结果表明：在轧件开始咬入与轧辊接触后，轧件表面的温度与应力急剧上升；由于接触摩擦与塑性变形功转化为热量，轧件在开始轧制时表面温度升高，进入粘着区后，由于摩擦消失，轧件表面温度略有下降，进入后滑区后，先略有回升接着平缓下降；由表及里，轧件的温度逐步降低。
关键词：热轧；温度场；应力场；三维
中图分类号：TF301 文献标识码：A 文章编号：1672-7207(2008)06-1262-05
Three-dimensional elastic-plastic finite element analysis of bar hot rolling process
XIANG Yong, TAN Jian-ping
(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: Based on the MARC, the 3-dimensional thermo-mechanical couple elastic-plastic finite elements simulation for the finished stand of bar hot rolling process was accomplished with renewed Lagrange. The material rheological model related to temperature, strain and strain rate was adopted, and the contact heat transfer condition was considered. The three-dimensional thermo-field analysis of round bar hot rolling process was accomplished. An equivalent heat method was proposed to analyse the temperature and stress fields of assembled roller. The results show that the temperature and stress at the surface of the bar increase rapidly at the beginning of contact occurring between the bar and rollers. The increase of the temperature of bar at the beginning of rolling is due to the heat transformed from the friction and plastic deformation work, and at stick zone, the surface temperature of bar decreases slightly because the friction vanishes at the stick zone, and then at the back slip zone, the temperature increases slightly and then decreases gently.
Key words: hot rolling; temperature fields; stress fields; three-dimensional
棒材轧制过程中，轧件在轧制区域的温度分布是十分重要的基础数据。不同温度下成型的产品其表面质量、力学性能指标均有所不同，同时，轧件的温度直接影响轧辊的受力与温度分布，它与产品质量、轧制工艺的制定及轧辊设计密切相关。本文作者基于Marc分析软件，考虑了温度、应变、应变率对材料流变应力的影响，轧辊与轧件导热系数、表面形貌及轧制压力等对界面接触传热的影响，对棒材热轧过程的温度场进行了三维大变形弹塑性耦合分析。
1 棒材轧制过程有限元模型
1.1 三维热弹塑性有限元控制方程
假设塑性应变增量{deP}能由塑性势f和Prandtl-Reuss流动定律导出，则塑性势f相当于屈服准则。当加工件内一单元的应力状态正好处于屈服面内，则其微分方程满足[1]：
在不考虑体力影响时，对于大变形-大应变条件，虚功原理的平衡方程为：
值得指出的是，若不考虑工件材料变形行为对应变速率与温度的影响，则在大变形控制方程中就不出现
项[2-8]。在这种情况下，材料的实际变形行为就不会很清楚。综合方程(3)与有限元中经常用到的方程，则：
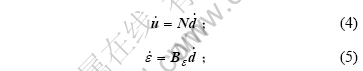
单元分割指将每一六面体单元分割成5个四面体单元。以定常应变四面体单元 (CST)为例，在三维热弹塑性问题中的四面体单元的4个矩阵N，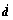
，
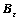和Be可以通过下列方法得到[9]：
为满足材料的不可压缩条件，假设将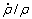
视为0，则有限元方程中的大变形-大应变刚度矩阵可以推 导为：
1.2 传热有限元模型
根据虚功原理，传热的能量平衡方程可表示为：
1.3 边界条件
热接触指2个产生接触的物体表面在传递机械载荷的同时还有接触表面之间的热量生成和交换，所以，轧制材料与轧辊表面的接触边界是一种热-力耦合的热接触，对轧件成形成性具有重要意义。
处理热接触要求程序同时支持接触分析和热-力耦合分析。MARC软件将先进的接触算法与热-力耦合功能相结合，可以支持热接触分析。MARC软件的接触分析可以处理刚性接触体和变形接触体。刚性接触体只需定义其外轮廓，用一簇直线/立方曲线或平 面/高斯曲面即可定义，而可变形接触体用位于结构边界上的常规单元即可定义。
沿着接触体边界的热传导用对流边界条件定义。
在两物体发生接触的接触界面处，发生接触换热，可表示为：
在棒材轧制过程中，轧件的温度为1 100 ℃左右，高温的轧件与低温的轧辊接触时，轧件的热量将通过轧件与轧辊之间的接触界面向轧辊传递，表征这种热量传递能力的是接触界面换热系数。接触换热系数是决定轧件和轧辊在轧制过程中的温度场和应力场以及轧制压力的一个主要因素，接触换热系数的确定对棒材轧制多物理场耦合分析具有重要的意义。
国内外学者对接触换热进行了广泛研究[10-11]。接触换热系数主要由如下几方面的因素决定：界面温度、热流与加热时间、加载及载荷滞后、实际接触面积、界面污染膜、表面形貌、介质材料、热流方向、表面氧化等。根据文献[12]的研究结果，构建棒材轧制轧件与轧辊之间的界面接触换热系数模型为：
可以通过接触热导试验确定，也可通过反问题法得到。
棒材与轧辊没有发生接触处主要是通过对流和热辐射的形式与环境空气发生换热，其边界条件为[13]：
对流换热系数一般取5 W/(m2·K)，辐射换热系数可通过下式进行计算[14-15]：
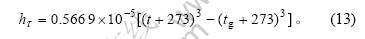
2 模拟结果与分析
轧件材质为低碳钢，轧件来料为椭圆形，孔型尺寸如图1所示。轧制后是直径为32 mm的圆棒，孔型尺寸如图2所示。轧件轧制前的温度为1 050 ℃，轧辊直径为560 mm，轧制速度为15 m/min，轧件长度取1 m进行计算。
本文基于有限元分析软件MARC，采用更新的Lagrange法描述的热力耦合大变形弹塑性有限元模型和四面体等参单元技术，材料的屈服准则采用Von Mises准则，流动法则采用Prandtl-Reuss法则。由于对称性，故可取轧件的1/2作为模拟对象。图3所示为三维有限元网格划分图。
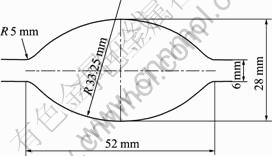
图1 K2孔型尺寸图
Fig.1 Cross-sectional shape of K2
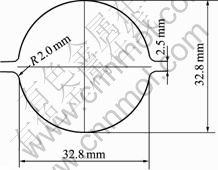
图2 K1孔型尺寸图
Fig.2 Cross-sectional shape of K1
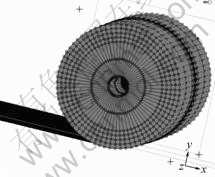
图3 有限元网格划分图
Fig.3 Grid of finite elements
分别取某截面处沿表面和轧件在截面中心部位从上到下的不同点在轧制过程中的温度演变情况。图4所示为表面所取点的位置，图5所示为这些点在轧制过程中的温度演变情况。图5中横坐标表示的是轧制过程中从咬入到轧制完毕的时间，纵坐标表示的是在轧制过程中这些点的温度变化。从图5可以看出，上部最先开始与轧辊接触的11 167节点，由于与冷轧辊表面接触而发生接触传热，且由于开始轧制时塑性变形较小，变形功小，其温度从开始轧制时的1 050 ℃迅速下降到958 ℃左右，随后，由于塑性变形产生的变形功增大及轧件表面与轧辊表面之间的摩擦功转化为热量，温度开始回升到接近1 050 ℃。坯料上表面的中心节点21 584，开始轧制时和轧辊表面不发生接触，塑性变形功转化为热量使其温度缓慢上升，而在发生接触后，在接触界面产生摩擦生热的同时与轧辊发生接触传热，温度缓慢降低到1 057 ℃后保持基本不变。表面上靠侧面的节点12 573和14 521的温度在整个轧制过程中除了在初始轧制时略有升高外，几乎没有变化。表面节点的温度演变取决于塑性变形功与摩擦功生热及节点处与轧辊之间的接触传热量。
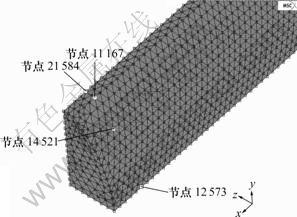
图4 表面取点位置图
Fig.4 Location of surface nodes
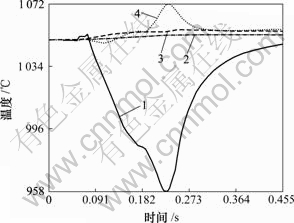
1—节点11 167；2—节点12 573；3—节点14 521；4—节点21 584
图5 表面点在轧制过程中的温度演变
Fig.5 Evolvement of temperature at surface in milling process
图6所示为轧件中心节点位置，图7所示为轧件横截面中心处从上至下不同点的温度演变情况。轧件在轧制过程中经历了前滑区、粘着区和后滑区。在前滑区21 584节点由于开始接触时的接触传热，且变形功较小，因而温度开始时略有降低，随着变形功与摩擦功增大，温度上升到1 072 ℃。进入粘着区时，轧件与轧辊之间没有摩擦，温度略微下降。在后滑 区，变形功与摩擦功的作用又使温度开始回升，但由于此时的变形功小于前滑区，因而，温度也相应较低。中心处的12 342点和21 484点的温度由于塑性变形功转化为热量，同时与周围相邻节点存在导热，二者作用的结果使温度略有上升，靠近表面的节点其变形量较大，因而，温度较高。
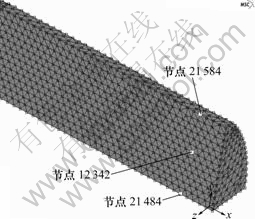
图6 中心取点位置图
Fig.6 Location of center nodes
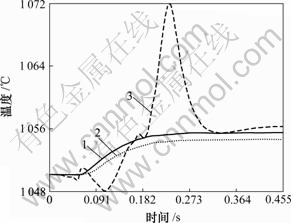
1—节点12 342；2—节点21 484；3—节点21 584
图7 截面中心处从上至下不同点的温度演变
Fig.7 Evolvement of temperature of nodes from top to down at section cross center
3 结 论
a. 建立了棒材热轧大变形热力耦合三维弹塑性有限元仿真分析模型并确立其热力边界条件，为棒材热轧过程的三维仿真分析提供了新的方法。
b. 棒材在轧制过程中表面最高温度为1 057 ℃，最低温度为958 ℃，芯部最高温度为1 072 ℃。
c. 得到了轧件从开始咬入到进入轧制前滑区、粘着区和后滑区整个过程中，轧件不同部位的温度的演变规律，为棒材热轧的孔型设计与工艺规程制定及轧辊设计提供有益信息。
参考文献：
[1] Park J J, Oh S I. Application of three-dimensional finite element analysis to shape rolling process[J]. Trans ASME J Eng Ind, 1990, 112: 36-46.
[2] Lee Y, Kim Y H, Approximate analysis of roll force in a round-oval-round pass rolling sequence, Journal of Materials Processing Technology, 2001, 113: 124-130.
[3] Bayoumi L S. Flow and stresses in a round-oval-round roll pass sequence, Int.J.Mech.Sci., 1998, 40(12): 1223-1234.
[4] Bayoumi L S, Lee Y S. Effect of interstand tension on roll load, torque and workpiece deformation in the rod rolling process, Journal of Materials Processing Technology, 2004, 145: 7-13.
[5] 何玉辉, 刘义伦, 邓高潮, 等. 工艺参数对铝板带热轧过程总温降影响的数值模拟[J]. 中南大学学报: 自然科学版, 2007, 38(4): 728-733.
HE Yu-hui, LIU Yi-lun, DENG Gao-chao, et al. Numerical simulation of influence of process parameters on aluminum plate’s temperature drop during hot rolling[J]. Journal of Central South University: Science and Technology, 2007, 38(4): 728-733.
[6] Kim S K, Im Y T. Three-dimensional finite element analysis of non-isothermal shape rolling[J]. Journal of Materials Processing Technology, 2002, 127: 57-63.
[7] Milenin A A, Dyja H, Mroz S, Simulation of metal forming during multi-pass rolling of shape bars[J]. Journal of Materials Processing Technology, 2004, 153-154: 108-114.
[8] Mori K, Osakada K. Finite element simulation of three- dimensional deformation in shape rolling[J]. Int J Num Meth Eng, 1990, 30: 1431-1440.
[9] Lin Z C, Lin S Y. An investigation of a coupled analysis of a thermo-elastic-plastic model during warm upsetting[J]. Int J Mach Tools Manuf, 1990, 30(4): 599-612.
[10] Rao S S. The finite element method in engineering[M]. 2nd ed. Oxford: Pergamon Press, 1989.
[11] 郝建伟, 曹建国, 张 杰, 等. 2250CVC热连轧机支持辊辊形研究[J]. 中南大学学报: 自然科学版, 2007, 38(4): 734-738.
HAO Jian-wei, CAO Jian-guo, ZHANG Jie, et al. Backup roll contour of 2250 CVC hot strip mill[J]. Journal of Central South University: Science and Technology, 2007, 38(4): 734-738.
[12] Shridar M R, Yovanovich M M. Elastoplastic contact conductance model for isotropic conforming rough surfaces and comparison with experiments[J]. Journal of Heat Transfer, 1966, 118(2): 3-9.
[13] Shridar M R, Yovanovich M M. Critical review of elastic and plastic thermal contact conductance models and comparison with experiment[J]. AIAA Journal of Thermophysics and Heat Transfer, 1994, 8(4): 633-640.
[14] Jiang Z Y, Tieu A K, Liu C, et al. Three-dimensional thermal-mechanical finite element simulation of ribbed strip rolling with friction variation, Finite Elements in Analysis Design, 2004, 40: 1139-1155.
[15] 周富强, 曹建国, 张 杰, 等. 基于神经网络的冷连轧机轧制力预报模型[J]. 中南大学学报: 自然科学版, 2006, 37(6): 1155-1160.
ZHOU Fu-qiang, CAO Jian-guo, ZHANG Jie, et al. Prediction model of rolling force for tandem cold rolling mill based on neural networks and mathematical models[J]. Journal of Central South University: Science and Technology, 2006, 37(6): 1155-1160.
收稿日期：2008-01-20；修回日期：2008-03-11
基金项目：国家重点新产品计划项目(2005ED770031)
通信作者：向 勇(1969-)，男，湖南龙山人，博士研究生，从事机械设计及理论研究；电话：0731-8830292；E-mail: xyong883@126.com
