基于四阶偏微分方程正则化的

多幅图像超分辨重建方法

黄淑英^{1, 2}，杨勇³，王国宇¹

(1. 中国海洋大学 电子工程系，山东 青岛，266100；

2. 江西财经大学 软件与通信工程学院，江西 南昌，330032；

3. 江西财经大学 信息管理学院，江西 南昌，330032)

摘要：基于重建的超分辨率方法中，图像求解是典型的不适定反问题，需借助有效的正则来稳定求解。针对二阶偏微分方程在重建图像中出现的块效应问题，引入四阶偏微方程的正则化处理，并用2-范数和四阶偏微分方程构造一种新的能量函数，提出一种新的超分辨率重建方法。通过仿真实验对比本方法与双三次插值和全变分方法重建高分辨率图像的差异。结果表明，该方法在抑制噪声的同时具有很好的保边缘能力。

关键词：超分辨率；图像重建；四阶偏微分方程

中图分类号: TP391.41          文献标志码：A         文章编号：1672-7207(2011)S1-0647-04

Multi-frame super-resolution reconstruction algorithm based on fourth-order partial differential equations regularization

HUANG Shu-ying^{1, 2}, YANG Yong³, WANG Guo-yu¹

(1. Department of Electrical Engineering, Ocean University of China, Qingdao 266100, China;

2. School of Software and Communication Engineering,

Jiangxi University of Finance and Economics, Nanchang 330032, China;

3. School of Information Technology, Jiangxi University of Finance and Economics, Nanchang 330032, China)

Abstract: Super-resolution image reconstruction (SRIP) is a typical ill-posed inverse problem, which can be stabilized by using a valid regular. To overcome the blocky effects of the conventional used second-order partial differential equations (PDE), a novel fourth-order PDE based method for SRIP was proposed, which is formed by incorporating the fourth-order PDE regularization in the image reconstruction. The method was developed by defining a new energy function from 2-norm and fourth-order partial differential equations. The simulation experiments of the proposed method were compared with those of bi-cubic interpolation method and total variation algorithm. The results show that the proposed method has better performance in suppressing noise with preserving edge.

Keywords: super-resolution; image reconstruction; fourth-order partial differential equations

超分辨率图像重建是将多幅模糊、有噪、频谱混叠后的多幅低分辨率降质图像，利用信号处理的方法融合估计出一幅高质量高分辨率图像的过程^[1]。图像超分辨率处理技术可突破图像采集设备的分辨率限制，充分利用多帧图像之间的互补信息，实现像素级的图像信息融合。该技术在计算机视觉、卫星遥感、天文学、生物医学成像、生物信息提取与识别等领域具有重要的应用价值^[2]。

多幅超分辨率重建算法主要分为频域和空域。频域中多幅超分辨率问题最早由Tsai 和 Huang^[3]提出，在此基础上人们不断对频域方法进行改进，Kim等^[4]提出了正则化的递归复原方法等。这类方法理论简单、运算复杂度低，但局限于全局平移运动、线性空间不变降质模型，且包含空域先验信息的能力有限，因而不再成为主流研究方法。为了弥补了频域方法的缺陷，空域方法得到了深入研究和广泛应用。空域方法主要包括非均匀插值方法^[5]、IBP迭代反投影法^[6]、POCS凸集投影^[7] 、ML概率估计^[8]、MAP概率估计法^[9]及混合ML/MAP/POCS方法^[10]。相对于频域方法，空域方法具有更大的灵活性和更广的适用范围。

近年来，偏微分方程法由于其对超分辨率重建这一不适定问题进行了正则化以及良好的降噪能力和保边缘能力，受到广泛的关注。全变分方法^[11]采用的就是二阶偏微分方程模型，尽管该方法在压抑噪声和保存边缘方面取得了很好的结果，但该方法在去除噪声的同时出现了阶梯效应。基于这一思想，本文作者提出了一种基于偏微分方程正则化的方法进行超分辨图像重建。考虑到图像的边缘区域和图像的平滑区域的特性，将全变分方法和四阶偏微分方程作为超分辨的正则化项。为了测试该方法的鲁棒性，对模拟图像序列进行了测试。

1  图像的降质模型

在超分辨率重建中，为了重构未知的高分辨率图像，必须了解理想图像与观测图像之间的关系，建立准确的、符合系统特性和实际成像条件的退化模型。给定一定场景的p幅低分辨率图像，可以认为它们是由一幅高分辨率图像经过一系列的降质过程产生的，降质过程包括几何运动、光学模糊、亚采样及噪声等。设低分辨图像Y_k是原始图像X经几何变形、线性空间可变模糊以及均匀离散采样作用后，与加性噪声叠加形成的第k幅低分辨率观测图像，大小为N₁×N₂。理

想的高分辨图像矢量为，N的大小为qN₁×qN₂，q是降采样因子。其退化过程可用数学模型描述为

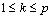,         (1)

式中：M_k 表示几何扭曲矩阵，大小为

；B_k 表示模糊矩阵，大小为；D_k为欠采样算子，大小为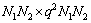；n_k 一般为加性零均值高斯白噪声，大小为。

2  超分辨率图像重建算法

2.1  四阶偏微分方程

二阶偏微分方程是通过最小化图像梯度的能量函数得到，而四阶偏微分方程是最小化图像拉普拉斯变换的能量函数。四阶偏微分方程的连续函数定义    为^[1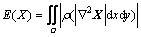2]：

            (2)

式中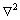：是拉普拉斯算子，是图像区域，函数是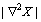的增长函数，满足如下条件：

                (3)

该函数的最小化就等价于平滑图像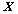。方程(2)对应的欧拉方程为

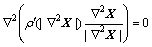       (4)

如果定义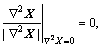 ，则式(4)可表示为

         (5)

则欧拉方程可以通过如下梯度下降法进行求解：

             (6)

式中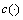：是一种边缘函数，用来控制扩散速度。

2.2  基于四阶偏微分方程的图像重建算法

多幅图像的超分辨重构为一个反问题，其求解是一个典型不适定问题，通常可以通过引入正则化项来克服病态。对于正则化问题，可通过最小化如下泛函来求解^[13]：

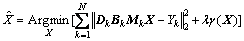     (7)

式中：表示重构图像，λ为正则化参数。右边第一项为数据逼近项，反映图像 对原始图像 f的逼近程度；第二项是正则项，保证恢复图像光滑，以去除噪声。采用正则化进行图像重建的方法中，全变分法是比较成功的方法之一，该模型本质上是一个针对图像本身的二阶偏微分方程处理模型，但二阶偏微分方程模型在进行图像复原时增强边缘，同时在平滑区域也产生阶梯效应^[14]。因此，在本文作者提出将四阶偏微分方程作为正则化项进行超分辨图像重建。将式(5)和式(7)进行结合，可得到式(7)对应的欧拉方程为：

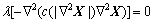          (8)

使用梯度下降法，高分辨率图像可以求得：

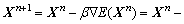
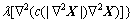            (9)

式中：n是迭代次数，β是时间步长。

3  实验结果和分析

为了验证本算法的有效性和鲁棒性，分别对模拟低分辨率图像做了一系列仿真实验，并与传统的三次样条插值算法和经典的全变分图像超分辨重建算法^[12]进行了实验比较。对于模拟仿真实验，除了进行直接视觉评估之外，还采用通用的信噪比作为定量评估  测度。

在模拟实验中，选取了256×256像素的标准Lena图像(见图1(a))，作为高分辨率图像背景，使用式(1)模型模拟生成低分辨率图像序列。实验中先使用标准差为1，尺寸为3×3的高斯低通滤波器来模糊图像，再让图像在水平和垂直方向上平移不同(奇数个)像素，对平移后图像进行下采样，采样因子为2，得到8幅具有亚像素平动、大小为128×128的低分辨图像。最后对所有的低分辨率图像加入均值为0，方差为0.001的高斯加性噪声，图1(b)所示为低分辨率图像序列中的一幅图像。

以得到的低分辨率图像序列为数据源，分别运用双三次插值、全变分和本文的方法对图像进行重建。图1(c)所示为对图像序列中第一幅图像进行双三次插值得到的结果。很明显可以看出：单幅图像的插值方法并没有起到抑制噪声的作用，也没能增强图像的边缘细节。图1(d)所示为全变分方法得到的重建结果。由图1(c)可以看出：该方法能去除噪声和保存边缘，但是对该图局部放大后(见图1(f))所示，可以看出，在平滑区域出现了大量的“块”效应。图1(e)所示为使用本方法进行重建得到的结果。从实验结果可以看出，该方法能有效地除噪声和保存边缘，视觉效果明显好于直接插值和全变分方法的结果。图1(g)所示为对其局部放大结果。从图中可以看出：在平滑区域并没有出现“块”效应。

图1  Lena图像的重建结果

Fig. 1  Reconstruction results of image Lena

为了定量评估本算法的有效性，表1所列为对其它图像含Cameraman、Barara模拟实验重建后的图像信噪比结果。从表1可以看出，本方法得到的重建图像的信噪比都得到提高。

表1   模拟实验重建后的信噪比对比结果

Table 1  Comparison results of signal to noise ratio for different methods on simulation reconstruction experiments

4 结论

(1) 针对二阶偏微分方程正则化方法在图像重建中产生块效应的问题，引入四阶偏微分方程作为正则化项，将其与2-范数组合构造了一种新的能量函数，提出了一种新的重建方法。

(2) 通过对模拟图像序列进行图像重建实验，可以看出本方法重建后的结果，在很好的压抑噪声的同时，既保存了图像的边缘，又增强了图像的对比度。对比分析实验结果表明：本方法是有效的，在主观视觉效果和客观评价指标上都优于双三次插值和全变分算法。

参考文献：

[1] Park S C, Park M K, Kang M G. Super-resolution image reconstruction: a technical overview [J]. IEEE Signal Processing Magazine, 2003, 20(3): 21-36.

[2] Katsaggelos A, Molina R, Mateos J. Super resolution of images and video [M]. Morgan and Claypool Publishers, 2007.

[3] Tai R, Huang T. Multi-frame image restoration and registration [C]//Advances in Computer Vision and Image Processing, 1984, 1(2): 317-339.

[4] Kim S P, Bose N, Valenzuela H. Recursive reconstruction of high resolution image from noisy undersampled multiframes[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1990, 38(6): 1013-102.

[5] Ur H, Gross D. Improved resolution from subpixel shifted pictures[J]. Graphical Models and Image Processing, 1992, 54(2): 181-186.

[6] Irani M, Peleg S. Motion analysis for image enhancement: Resolution, occlusion, and transparency [J]. Journal of Visual Communication and Image Representation, 1993, 4(4): 324-335.

[7] Patti A J, Sezan M I, Tekalp A M. Superresolution video reconstruction with arbitrary sampling lattices and nonzero aperture time [J]. IEEE Transactions on Image Processing, 1997, 6(8): 1064-1076.

[8] Tom B C, Katsaggelos A K. Reconstruction of a high resolution image from multiple-degraded mis-registered lowresolution images [C]//Proceedings of SPIE-Visual Communications and Image Processing, 1994: 971-981.

[9] Belekos S P, Galatsanos N P, Katsaggelos A K. Maximum a Posteriori video super-resolution using a new multichannel image prior [J]. IEEE Transactions on Image Processing, 2010, 19(6): 1451-1464.

[10] Elad M, Feuer A. Restoration of a single superresolution image from several blurred, noisy, and undersampled measured images [J]. IEEE Transactions on Image Processing, 1997, 6(12): 1646-1658.

[11] Ng M K, Shen H, Lam E Y, et al. A total variation regularization based super-resolution reconstruction algorithm for digital video [J]. EURASIP Journal on Advances in Signal Processing, 2007, ID 74585, 16 pages.

[12] You Y L, Kaveh M. Fourth-order partial differential equations for noise removal [J]. IEEE Transactions on Image Processing, 2000, 9 (10): 1723-1730.

[13] Farsiu S, Robinson M D, Elad M, Milanfar P. Fast and robust multiframe super resolution [J]. IEEE Trans Image Processing, 2004, 13(10): 1327-1344.

[14] Chan T, Marquina A, Mulet P. High-order total variation-based image restoration [J]. SIAM Journal on Scientific Computing, 2000, 22(2): 503-516.

(编辑 龙怀中)

收稿日期：2011-04-15；修回日期：2011-06-15

基金项目： 国家自然科学基金资助项目(60963012)；教育部科学技术研究重点项目(211087)；江西省自然科学基金资助项目(2010GZS0052)；江西省教育厅科技项目(GJJ10125，GJJ11415)

通信作者：黄淑英(1977-)，女，山东德州人，博士研究生，讲师；从事图像处理与模式识别技术研究；E-mail: greathsy@sohu.com