质量特性测试平台负载作用下的干扰力矩

王福生，包钢，杨庆俊

(哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨，150001)

摘要：针对负载作用下质量特性测试平台弹性变形引起干扰力矩的问题，研究浮起平台负载作用下产生干扰力矩的规律。根据弹性力学薄板弯曲理论，推导出在负载作用下有限元单元质心位移公式及结构整体质心弹性位移公式，给出浮起平台的干扰力矩公式，计算质量特性测试平台在测量过程中质心的弹性位移和由此产生的干扰力矩。研究结果表明：平台变形引起的干扰力矩为偏航角ψ的函数，幅值为平台自身重力和质心位移的乘积。分析结果为测试平台的结构设计和测试精度的提高提供了依据。

关键词：质量特性；有限元；质心；干扰力矩

中图分类号：TJ306；TB124          文献标志码：A         文章编号：1672-7207(2011)10-3048-06

Disturbance torque acted on by load for mass properties measuring instrument

WANG Fu-sheng, BAO Gang, YANG Qing-jun

(School of Mechanical and Electrical Engineering, Harbin Institute of Technology, Harbin 150001, China)

Abstract: Based on the problem of disturbance torque caused by the elastic deformation existing in the load platform acted on by load, the laws of disturbance torque from the load platform were researched. According to the theory on the lamella bending of elastic mechanics, the formulary for the element center of mass displacement of the finite element and for the platform structure center of mass elastic displacement was deduced. And the disturbance torque formulary about the platform was given. Central mass elastic displacement resulting from deformation of the platform of mass properties measuring instrument acted on by load and the disturbance torque resulting from the displacement were calculated. The results show that the disturbance torque is ψ function, and the amplitude is the product of platform gravity and central mass displacement. The research results provide bases for the structure design of the measuring instrument platform and the improvement of measuring precision.

Key words: mass properties; finite element; center of mass; disturbance torque

质量特性参数主要包括物体的质量、质心、转动惯量、惯性积等^[1]，是高速远程飞行物体自动控制及测试的重要参数^[2-3]，也是众多工程领域所关心的重要参数^[4]。因此，在航空航天及军事等领域，质量特性参数测试设备起着极为重要的作用^[5]。早在20世纪60年代，美国Spaco Inc公司的质量测量实验室就对刚体和液体的质量特性参数的测量进行了研究^{[4, 6]}。迄今为止，美国肯尼迪航天中心^[7-8]、Space Electronics Inc^[9]等研究机构已经开发出一系列精度高、自动化水平高的质量特性测试设备。我国从20世纪80年代开始较为系统地研究开发质量特性参数测试设备^[10-12]，但质量特性测试设备集成化程度不高，精度低，自动化程度低。随着对质量特性测试设备要求的提高，亟待研究高精度、高效率的质量特性测试平台。为此，本文作者在充分了解国内外质量特性测试方法和进展的基础上，采用一种以半球气浮轴承为支点的质心、转动惯量测量的一体化质量特性测试方案。测试平台依靠压缩空气在气浮轴承与轴承座之间形成的气膜使平台浮起，从而实现近似无摩擦的相对运动，大大提高了测试精度。平台质心采用不平衡力矩法测量，转动惯量采用扭摆法测量，1次安装就可以测出试件的质心和转动惯量，实现了质量特性的快速测量。国内外质量特性测试平台研究中多将浮起平台视为刚体，而对受力变形引起平台质心变化对测量精度的影响忽略不计。但当质量特性测试平台精度要求较高时，负载引起的平台质心变化将产生干扰力矩，带来质心测量误差。浮起平台采用圆柱板式结构，在负载作用下平台的变形为小变形。本文根据弹性力学薄板弯曲理论推导出负载作用下有限元单元质心位移公式及结构整体质心弹性位移公式，计算质量特性测试平台在测量过程中质心的弹性位移和由此产生的干扰力矩，研究浮起平台负载作用下产生干扰力矩的规律，以便为平台的结构设计和测试精度的提高提供依据。

1  浮起平台的有限元模型

1.1  浮起平台的结构

质量特性测试平台结构如图1所示。台体(浮起部分)由半球气浮轴承支撑，悬浮于空中，气浮轴承既为转台又为中心轴。用1根空心管穿过球轴承的基座，空心管的下端装在圆柱气浮轴承上，气浮轴承与测力传感器相连接，吊起后形成一个刚性结构，在测量过程中保持平台水平状态。采用刚性低偏置力矩传感器，可以精确测量力和力矩，而且不必配重或调平。浮起部分采用铝制平台做好，质量较小，其材料参数如下：弹性模量为69 MPa，泊松比为0.32，密度为2.7 t/m³。

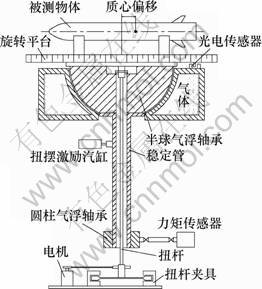
图1  质量特性测试平台机构示意图

Fig.1  Sketch of mass properties measuring instrument

1.2  有限元模型

将气浮轴承半球视为刚体，在单元选取过程中可将其视为1个质量点。设计台面厚度与直径比小于1:5，可作为薄板弯曲问题考虑^[13]，采用板壳单元。在小变形情况下，平板的横向位移u与面内位移v互不相关、不相耦合。可由平面应力单元求出单元的横向质心位移ω_c以及单元的面内质心位移u_c和v_c。

薄板的厚度远远小于薄板的平面尺寸，考虑KIRCHHOFF假设，薄板弯曲有如下几个方程^[14]。

将纵向位移u和v用挠度ω表示的薄板中位移分量和应变分量方程为：

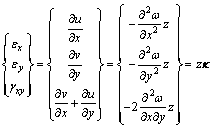     (1)

式中：ω为挠度，正向取为z轴的正方向；ε_x为x向应变；ε_y为y向应变；γ_xy为xy面剪应变；κ为薄板的广义应变。

应力分量用挠度ω表示，薄板的物理方程为：

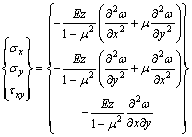       (2)

式中：σ_x为x向正应力；σ_y为y向正应力；τ_xy为作用在垂直于x轴的面上，沿着y轴方向的剪应力；E为材料的拉压弹性模量；μ为泊松比。

薄壳单元以薄板最小势能原理作为变分基础，系统总位能泛函表达式为：

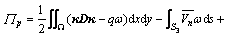
               (3)

式中：Ω为求解域；D为弹性系数矩阵，对于各向同性材料，其表达式为：

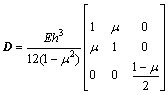
式中：h为薄板厚度；q为作用于薄板表面的分布载荷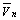；为边界S₃上横向载荷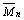；为边界S₂和S₃给定力矩；s为边界的切线方向；S₂为简支边；S₃为自由边。

进一步执行有限元分析的步骤，可以得到节点的求解方程。则对于平面应力四节点矩形单元，选择广义坐标和位移多项式如下：

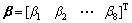
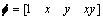             (4)

单元的位移列阵为：

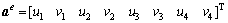   (5)

平面内单元的质心位移为

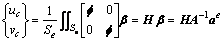    (6)

式中：S_e为单元的面积；A为与单元坐标有关的已知系数矩阵。

基于Mindlin平板理论，薄板中面离散为矩形单元，则任意节点i(i=1，2，3，4)的节点位移有挠度ω_i、绕x轴转角θ_xi和绕y轴转角θ_yi。若把转角看作矢量，则它们以指向节点为正，挠度以沿z轴正向为正。单元质心挠度变形量为：

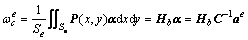   (7)

式中：

P(x,y)=[1  x  y  x²  xy  y²  x³  x²y  y³  x³y  xy³]；

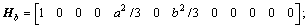式中：α为薄板挠度系数矩阵；C为相对于挠度模式依赖于结点坐标的已知矩阵。综合式(6)和(7)可得各单元的质心位移量。

2  平台质心变化量公式

浮起平台做刚体运动，在刚体运动的平台内各质点又进行微小的弹性变形运动，对平台测量过程进行刚柔耦合运动分析，研究在其测量过程中浮起平台的质心变化量。

考虑可变形体的质心运动。如图2所示，XYZ为惯性坐标系。假设O点是运动发生前物体的质心位置(即刚体质心)，C点为物体变形后的质心，以O点为原点建立结体坐标系xyz。P_i点为1个任意质点。由于物体内各质点发生位移使物体的质心位置发生变化，质心O点运动到C点。由图2可知有如下关系式^[15]：

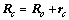              (8)

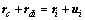             (9)

式中：R_c为物体变形后的质心在整体系中的整体位置矢量；r_c为质心在结体系中的变形矢量；r_di为质点运动到D_i后相对于变形后质心的位置矢量。

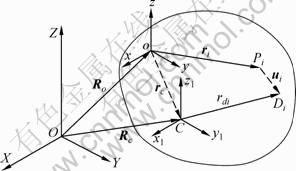
图2  质心位移图

Fig.2  Center of mass displacement

考察如图2所示n个质点P_i(或质点D_i)组成的质点系S，则有：

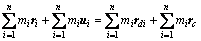    (10)

式中：m_i为质点P_i(或质点D_i)的质量。

注意到C为变形体的质心，O为刚体的质心，有：

；

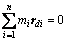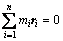
将上式代入式(10)得变形体的质心位移为：

          (11)

式中：m为浮起平台的质量。

3  干扰力矩计算公式

在浮起平台回转中心建立相对地球静止的惯性坐标系XYZ和随平台转动的结体坐标系xyz。当浮起平台转动时，其姿态可由3个欧拉角表示。

设在初瞬时，结体坐标系和惯性坐标系重合，当给定一组欧拉角(ψ，θ，f)时，按z，y和x顺序由3次连续转动唯一确定平台的方位。因此从惯性坐标系到结体坐标系的变换矩阵C可以表示为^[16]：

(12)

式中：ψ为偏航角；θ为俯仰角；f为滚动角。浮起平台在结体坐标系中自身重力场为：

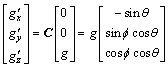      (13)

当浮起平台偏转时，由于负载压力作用平台质心将产生偏移，平台自身重力产生的干扰力矩为：

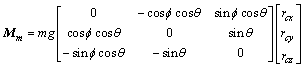(14)

式中：r_cx为平台质心沿结体系x轴的偏移量；r_cy为平台质心沿结体系y轴的偏移量；r_cz为平台质心沿结体系z轴的偏移量。

4  计算结果与分析

浮起平台结构尺寸如下：中心孔半径R_zx为38 mm，平台外圆半径R_pt为200 mm；平台厚度h为8 mm。初始位置结体坐标系与惯性坐标系重合，平台受力点沿结体系x轴关于平台中心对称分布。图3所示为浮起平台水平时负载作用下的变形图。

4.1  浮起平台的质心位移

利用上述有限元模型及平台质心变化量公式，计算试件不同质心位移(试件质心与回转中心的距离)、不同受力点的浮起平台质心位移量r_c。z轴的质心位移不会产生干扰力矩，这里重点研究浮起平台沿x轴、y轴的质心位移。

设初始状态浮起平台的回转中心与刚体质心重合，在水平状态下平台仅受到垂直方向的压力作用。在初始位置时，试件质心置于结体系x轴上，平台变形关于x轴对称，平台y轴质心位移量为0 mm。研究试件质心位移不同时，平台可变形体的质心位移规律。根据计算的质心位移r_c，绘制平台可变形体x轴质心随试件质心与回转中心的距离变化曲线，如图4所示。

图3  平台变形图

Fig.3  Platform deformion

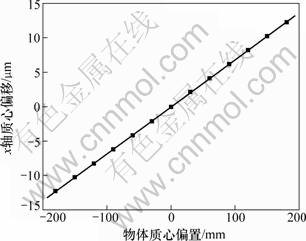
图4  平台x轴质心位移曲线

Fig.4  Mass displacement curve of x-axis center

从图4可以看出：平台x轴质心位移量与试件质心位移为线性关系，平台的质心位移量随着试件质心与回转中心的距离的增加而增加。当物体质心位移等于平台半径R_pt时，x轴质心位移r_cx|pt为13.66 μm，图4中的曲线表达式可描述为：

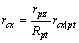             (15)

式中：r_pz为试件质心与回转中心的距离。

设平台z轴质心位移量为r_cz，由r_cx和r_cz可以得出试件质心位移相同时，平台可变形体质心在惯性坐标系中的位置为：

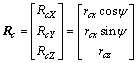          (16)

式中：R_cX，R_cY和R_cZ分别为平台质心位移量在惯性坐标系中X，Y和Z方向的分量。

4.2  负载作用下的干扰力矩

由上面分析知初始位置结体坐标系和惯性坐标系重合，平台在负载作用下产生的质心位移在y轴的分量为0，即r_cy=0。这时，平台受力变形后自身重力产生的干扰力矩对结体系各轴的投影分量为：

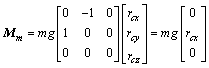     (17)

从式(17)可以看出：平台y轴干扰力矩M_my仅与r_cx有关，因此，M_my也与试件质心位移呈线性关系。经计算可知：当物体质心位移等于平台半径R_pt时，y轴干扰力矩M_my|pt为4.10×10^-4 N·m，M_my的表达式为

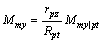            (18)

以试件质心位移120 mm为例，绘制在惯性系中，平台绕Z轴旋转时自身重力产生的Y轴、X轴干扰力矩曲线如图5所示。从图5可以看出：随着平台绕惯性参考系Z轴旋转，由于平台质心位移产生的对Y轴、X轴的干扰力矩分别为一余弦曲线和正弦曲线，当ψ为0°和180°时，M_mY达到最大值；当ψ为90°和270°时，M_mX达到最大值；当试件质心位移120 mm时，对Y轴、X轴干扰力矩的最大值都为2.46×10^-5 N·m。

利用上面的有限元模型和的平台质心变化量公式，计算得被测物体质心任意偏置量、Z轴任意转角的平台弹性变形引起的干扰力矩M_m，如图6所示。

由式(18)和图5得平台质心位移对惯性坐标系的干扰力矩为：

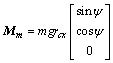           (19)

从式(19)可以看出：平台受力变形引起的质心位移对惯性坐标系的干扰力矩为角ψ的函数，幅值为平台自身重力和平台质心位移的乘积，干扰力矩取决于平台的质心位移。

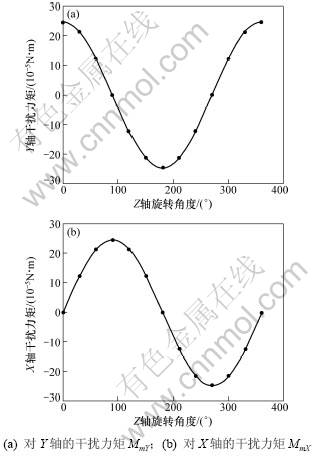
图5  平台绕Z轴旋转时的干扰力矩

Fig.5  Unbalance moments when rotated around Z-axis

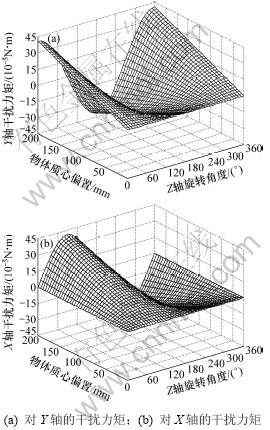
图6  平台弹性变形引起的干扰力矩

Fig.6  Unbalance moment resulted from deformation

平台在负载作用下，质心位移引起的干扰力矩是由于平台弹性变形而产生的。试件质心位移越大，平台弹性变形产生的干扰力矩就越大；当试件质心与平台回转中心重合时，平台xy平面各方向的弹性变形相等，平台自身重力不产生干扰力矩。因此，在质量特性测量中，应估算被测物体的质心，尽量使被测物体的质心与平台的回转中心重合，减少平台弹性变形引起的干扰力矩，减少测量误差。在平台结构设计中，应在考虑平台自身重力的基础上，采用弹性模量大的材料，提高平台的结构刚度，以减小平台的弹性变形，提高测量精度。

5  结论

(1) 当试件质心与平台回转中心重合时，浮起平台xy平面各方向的弹性变形相等，不产生干扰力矩。

(2) 在结体坐标系中，对同一个试件平台，可变形体的质心位移量只与试件质心和回转中心的距离相关。平台质心位移量与试件质心位移呈线性关系，质心位移量随试件与回转中心距离的增加而增加；平台受力变形产生的干扰力矩与试件质心位移呈线性关系，干扰力矩随试件质心与回转中心距离的增加而  增加。

(3) 绕Z轴旋转时，平台质心位移产生的对惯性坐标系X轴、Y轴的干扰力矩为角ψ的函数，分别为正弦曲线和余弦曲线，幅值为平台自身重力和质心位移的乘积，其最大值均为结体坐标系中的y轴干扰力矩。

参考文献：

[1] Richard B, Kurt W. Mass properties measurement handbook, sawe paper No.2444[R]. Los Angeles: Society of Allied Weight Engineers, 1998: 5-9.

[2] Asker-Ali A, Adil B G. Investigation of center of mass by using magic squares and its possible engineering applications[J]. Robotics and Autonomous Systems, 2004, 49(9): 219-226.

[3] Sergei T, Trevor W. Mass property estimation using coasting maneuvers[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(4): 625-632.

[4] George C. Annual report: Research and development in the field of physical determination of mass properties[R]. Alabama: Spaco, Inc, 1965: 1-8.

[5] John P, Bruce V B. Estimation of spacecraft mass properties using angular rate gyro data[C]//1992 AIAA/AAS Astrodynamics Conference. Washington: American Institute of Aeronautics and Astronautics, 1992: 21-26.

[6] George C. Final report: Research and development in the field of physical determination of mass properties[R]. Alabama: Spaco, Inc, 1966.

[7] Wolcott K R, Graham T A, Doty K L, et al. Innovative mechanism for measuring the mass properties of an object[C]//The 28th Aerospace Mechanisms Symposium. Florida: NASA Lewis Research Center, 1994: 107-121.

[8] Doty K L. Mass properties measurement system dynamics and statics measurements[R]. Florida: University of Central Florida, 1993: 111-134.

[9] Space Electronics Inc. Combined center of gravity and moment of inertia measurement[EB/OL]. [2009-09-28]. http://www.space-electronics.com/Products/KSR_Series.php.

[10] 赵新通, 韩俊伟, 何景峰, 等. 带动压反馈的质心测量系统电液伺服控制方法[J]. 机床与液压, 2008, 36(6): 51-53.
ZHAO Xin-tong, HAN Jun-wei, HE Jin-feng, et al. Electro-hydraulic servo control method for gravity center position measure system with dynamic pressure feedback[J]. Machine Tool & Hydraulics, 2008, 36(6): 51-53.

[11] 唐文彦, 李慧鹏, 张春富. 扭摆法测量飞行体转动惯量[J]. 南京理工大学学报: 自然科学版, 2008, 32(1): 69-72.
TANG Wen-yan, LI Hui-peng, ZHANG Chun-fu. Measurement of flight object’s moment of inertia using torsion pendulum[J]. Journal of Nanjing University of Science and Technology: Natural Science, 2008, 32(1): 69-72.

[12] 吴斌, 张波, 许苏海. 导弹质量特性测量装置设计[J]. 上海航天, 2001, 18(3): 41-44.
WU Bin, ZHANG Bo, XU Su-hai. Mass property instrument design for missile system[J]. Aerospace　Shanghai, 2001, 18(3): 41-44.

[13] 杨骊先. 弹性力学及有限单元法[M]. 杭州: 浙江大学出版社. 2002: 143-149.
YANG Li-xian. Elastic mechanic and finite element method[M]. Hangzhou: Zhejiang University Press, 2002: 143-149.

[14] 赵经文, 王宏钰. 结构有限元分析[M]. 北京: 科学出版社, 2001: 75-82.
ZHAO Jing-wen, WANG Hong-yu. Structure finite element analysis[M]. Beijing: Science Press, 2001: 75-82.

[15] 洪善桃. 高等动力学[M]. 上海: 同济大学出版社, 1996: 142-153.
HONG Shan-tao. Advanced dynamics[M]. Shanghai: TongJi University Press, 1996: 142-153.

[16] Greenwood D. Principles of dynamics[M]. 2nd ed. New Jersey: Prentice-Hall, 1988: 371-380.

(编辑 陈灿华)

收稿日期：2010-10-15；修回日期：2010-12-28

基金项目：国家高技术研究发展计划(“863”计划)项目(2002AA742049)

通信作者：王福生(1979-)，男，山东菏泽人，博士研究生，从事质量特性测量、气压传动与控制方面的研究；电话：0451-86413446；E-mail：wangfs0822@163.com