DOI: 10.11817/j.issn.1672-7207.2015.03.039
考虑指数流的真空预压竖井地基固结解析解
李菲菲1, 2,谢康和1, 2,邓岳保1, 2
(1. 浙江大学 滨海和城市岩土工程研究中心,浙江 杭州,310058;
2. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州,310058)
摘要:传统固结理论认为渗流速度和水力梯度呈线性关系,但在软塑性土地基中常出现背离线性关系的情况,即为非达西渗流模式。在经典竖井地基固结理论的基础上,假设孔隙水渗透服从指数渗流模式,并结合真空预压的边界条件,建立新的竖井地基固结计算模型,获得超静孔压和径向固结度的严格解答,并通过开展多工况算例对比,分析指数渗流模型参数和真空压力沿竖井衰减系数等对竖井地基固结计算结果的影响效应。研究结果表明:非达西渗流指数m对固结速率影响最为显著,在固结初期,m越大,固结速率越快;在固结后期,m越小,固结速率越快;涂抹区参数s及κh/κs越大,竖井地基固结速率越慢;负压衰减系数k1和k2、真空荷载p0越大,固结速率越快。
关键词:竖井;指数渗流;真空预压;固结解析解
中图分类号:TU443 文献标志码:A 文章编号:1672-7207(2015)03-1075-07
Analytical solution for consolidation by vertical drains with exponential flow under vacuum preloading
LI Feifei1, 2, XIE Kanghe1, 2, DENG Yuebao1, 2
(1. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;
2. Key Laboratory of Soft Soils and Geoenvironmental Engineering of Ministry of Education,
Zhejiang University, Hangzhou 310058, China)
Abstract: According to the traditional consolidation theory, the velocity of flow v is linearly related to the hydraulic gradient. But the case is not true with high plastic clay. On the basis of the traditional and classic consolidation theory of vertical drains, supposing that v is exponentially related to i, and taking into consideration the boundary conditions of the vacuum preloading, a new consolidation computation model of vertical drains was established and the corresponding solution of excess pore water pressure and radial degree of consolidation was obtained exactly. Based on the solution, the consolidation behavior of the vertical drained ground with exponential flow was investigated by parameters study. The results show that the non-Darcian flow exponent has the most important influence on consolidation rate. In initial stages of consolidation, the increase of m can accelerate the consolidation rate and make the consolidation rate slow down in the later stage. The increase of s and κh/κs can make the consolidation rate slow down. The increase of the vacuum reduction factors kl, k2 and p0 can raise the consolidation velocity.
Key words: vertical drain; exponential flow; vacuum preloading; analytical solution for consolidation
Terzaghi传统固结理论中通常假定孔隙水在土骨架中的渗透服从简单的达西渗流定律。然而,高塑性黏土中孔隙水的渗流速度和水力梯度之间并非简单的线性关系,即为非达西渗流。其中较常用的非达西渗流模式主要包括3类,即Hansbo[1]提出的非达西渗流模式、Miller等[2]提出的起始比降模式及Slepicka[3]提出的指数渗流模式。鉴于非达西渗流现象的存在,学者们相继对考虑非达西渗流的固结问题展开了研究。刘忠玉等[4-5]利用有限差分法对基于起始比降模型和Hansbo渗流模型的软土一维固结问题进行了求解。Xie等[6]基于起始水力坡降模式,给出了变荷载作用下软土一维固结问题的近似解。王坤等[7]对考虑起始水力坡降的软土一维固结理论进行了深入分析。之后,李传勋等[8]较系统地研究了基于指数形式渗流模型的单层及多层地基一维固结问题。相对而言,考虑非达西渗流的竖井地基固结问题研究则较少。数值求解方面,Teh等[9-10]利用有限单元法对考虑Hansbo非达西渗流的竖井固结问题进行了研究。解析求解方面,Hansbo[11]推导了基于Hansbo渗流的竖井地基固结近似解;Walker等[12]在忽略井阻的情况下推导了指数渗流模式下竖井地基固结解析解(以下简称walker解)。近年来,真空预压法在软土地基处理中得到广泛应用[13-15]。为此,本文作者拟在walker解基础上,结合真空预压的边界条件,推导考虑指数渗流模型下竖井地基固结解答。
1 计算模型
1.1 计算简图
图1所示为考虑涂抹作用的竖井地基径向固结问题的计算简图。井周土体分为涂抹区、未扰动区。图1中:rw为竖井的半径;l为竖井的长度;rs为涂抹区的半径;re为竖井影响区半径;r和z分别为径向及竖向坐标。参考文献[14],假设真空压力沿深度由-p0变为-k1p0,同时在径向由-p(z,rw)变为-k2p(z,rw)。地基底部及外围均不透水,仅顶部透水。
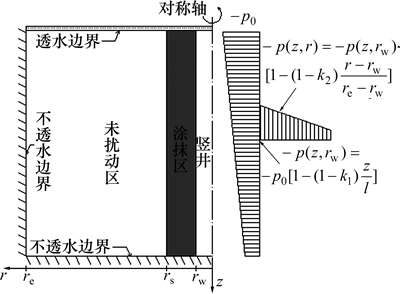
图1 竖井地基径向固结问题计算简图
Fig. 1 Diagrams for radial consolidation of soil by vertical drain
1.2 基本假定
基本假定如下:
1) 等应变条件成立,即假定竖井地基中无侧向变形,同一水平面上各点的竖向变形是相等的。
2) 竖井内孔压(即超静孔隙水压力)沿径向的变化很小,可以不计;且任一深度z处从土体中沿井周流入竖井的水量等于竖井中向上水流的增量。
3) 塑料排水板(PVC)的井阻可忽略不计。径向和竖向渗流可以单独考虑。考虑竖向渗流时按太沙基一维固结理论,考虑径向渗流时 kv=0,径竖向组合渗流可按Carrillo定理考虑。故本文只需考虑径向固结。
4) 参考文献[14],假定竖井影响区内,真空压力沿竖向和径向均线性变化。
5) 渗流服从Slepicka(1960)指数渗流模式[3] ,即
 (1)
(1)
式中:v为渗流速度; 为非达西渗流条件下的渗透系数;m为非达西渗流指数;i为水力坡降。m与水力坡降的大小密切相关。当水力坡降较小时,m>1;当水力坡降较大时,m<1;m=1,即为达西定律。
为非达西渗流条件下的渗透系数;m为非达西渗流指数;i为水力坡降。m与水力坡降的大小密切相关。当水力坡降较小时,m>1;当水力坡降较大时,m<1;m=1,即为达西定律。
2 控制方程及其求解条件
2.1 控制方程
参考文献[14],竖井影响区内任一点的真空压力为
 (2)
(2)
由此可得任意一点的静水头为
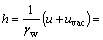
 (3)
(3)
由式(3)对进行r求导,可得水力梯度i为
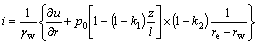 (4)
(4)
将式(4)代入式(1)可得涂抹区和未扰动区的渗流速度为
 (5)
(5)
式中:-p0为真空预压时砂垫层中z=0的负压;kl为竖井底部负压与顶部负压的比,其值不大于1;k2为竖井影响区r=rw处与r=re处的负压比,其值不大于1;κs和κh分别为涂抹区及未扰动区的土体渗透系数;γw为水重度;u为影响区内任一点的孔压;l为地基软土层厚度。
采用轴对称坐标系,取影响区内半径为r处厚度为dr的环微元,如图2所示。由流入和流出该环微元的水量变化等于其体积的变化可得
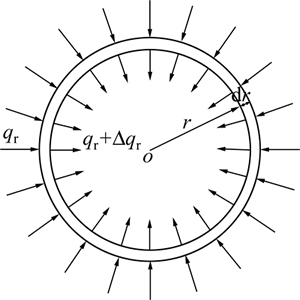
图2 轴对称坐标系下土体微元
Fig. 2 Axisymmetric unit cell
 (6)
(6)
其中: ,
,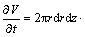
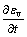 。将式(5)代入式(6),整理可得等应变条件下非达西渗流控制方程:
。将式(5)代入式(6),整理可得等应变条件下非达西渗流控制方程:
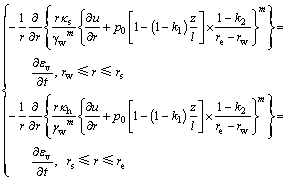 (7)
(7)
其中:
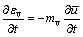 (8)
(8)
mv为土的体积压缩系数; 为仅考虑径向渗流时影响区内土中任一深度的平均孔压,可表示为
为仅考虑径向渗流时影响区内土中任一深度的平均孔压,可表示为
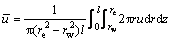 (9)
(9)
2.2 求解条件
边界条件:
1)  ;
;
2)  ;
;
初始条件: 。
。
式中:uw为仅考虑径向渗流时竖井内任一深度的孔压; 为初始孔压。
为初始孔压。
3 方程的求解
3.1 控制方程的转换
方程(7)两边对r积分,利用边界条件2),并代入式(8)可得
 (10)
(10)
式中: ,κ=κh/κs。
,κ=κh/κs。
取y=r/rw,n=re/rw,s=rs/rw,则通过转换式(10)变为
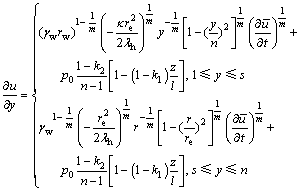 (11)
(11)
对上式中含y的项进行级数展开得
 (12)
(12)
其中:{x}c为阶乘幂或升阶乘,即为
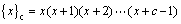 ,
,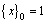 (13)
(13)
对于式(11)两边关于y积分,含y的项利用式(12)进行级数展开,并利用求解条件1),可得
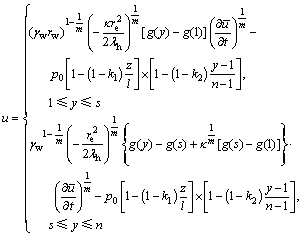 (14)
(14)
式中:g(y)为式(12)对y积分,
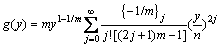 (15)
(15)
对式(9)所示的平均孔压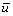 ,进行坐标系转换得
,进行坐标系转换得
 (16)
(16)
将式(14)代入式(16)中可得
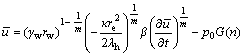 (17)
(17)
式中:
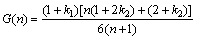 (18)
(18)
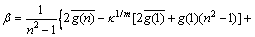
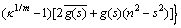 (19)
(19)
 为y与式(15)的乘积对y积分所得,即
为y与式(15)的乘积对y积分所得,即
 (20)
(20)
3.2 控制方程的解析解
对于式(17)所示的控制方程,可得
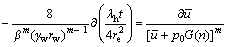 (21)
(21)
进一步整理可得
 (22)
(22)
式中: ;
; ;
; 。
。
对形如式(22)的方程,在m≠1时,根据求解条件3)可解得
 (23)
(23)
式(23)也可用无量纲 来表达:
来表达:
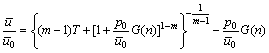 (24)
(24)
式中: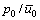 为真空压力比。
为真空压力比。
则可得任意时刻径向固结度Ur为
 (25)
(25)
将式(13)代入式(10)中可得
 (26)
(26)
式(23)~(26)即为单面排水考虑指数渗流模式的真空预压竖井地基固结解析解。
4 解析解验证及分析
4.1 算例及计算工况
本文采用Teh等用过的单井地基算例[9]。单井圆柱体影响域直径de=4 m,涂抹区直径ds=0.4 m,竖井直径dw=0.1 m,即n=40,s=4;竖井打设深度l=10 m。
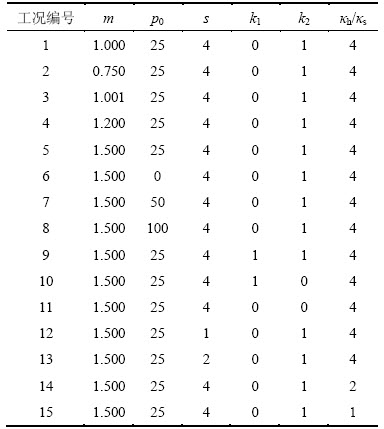
本文将着重分析非达西渗流指数m、真空荷载p0、涂抹区厚度比s、渗透系数比κh/κs及衰减系数k1和k2对固结度的影响,对如表1所示15种工况进行计算分析。工况1为达西渗流模式,涂抹区(ks)、水平向(kh)渗透系数取kh=10-8 m/s,kh/ks=4。工况5为非达西渗流标准工况,涂抹区(κs)、水平向(κh)的渗透系数取κh=10-8 m/s,κh/κs=4。压缩模量Es=10.0 MPa, =50 kPa,真空压力比VPR=
=50 kPa,真空压力比VPR=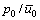 =0.5。
=0.5。
此外,非达西渗流指数m取值方面,Hansbo认为m=1.5与实测结果较吻合[11],Teh等[9]认为m可以取1.2~1.5。工况3为当m接近于1时的情况,目的是与m=1的达西渗流解析解进行对比验证。
表1 计算工况与参数
Table 1 Calculation conditions and parameters
4.2 结果对比与分析
为验证本文解析解的可靠性,需与现有基于达西渗流的真空预压单井地基固结解析解进行对比分析。对于达西渗流情况,参考文献[14]可知任意时刻t无量纲超静孔压为
 (27)
(27)
式中:
 ;
; ,
,
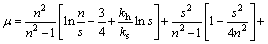
 。
。
达西渗流理论解(工况1)、本文非达西流理论解的对比如图3所示。由图3可知:当非达西渗流指数m接近1时,非达西渗流与达西渗流模式计算结果差异很小,这从一个方面说明了本文给出解析解的正确性。
此外,当取负压p0=0,本文解即退化为文献[12]中的解,从而进一步验证了本文解析解的正解性。
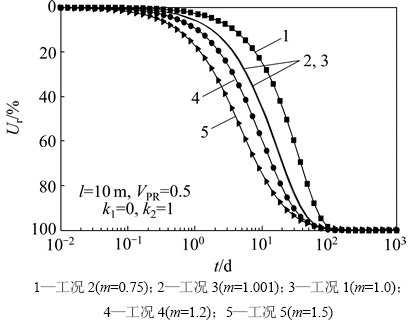
图3 非达西渗流指数m对固结度的影响
Fig. 3 Influence of m on consolidation rate
从图3还可以看出:非达西渗流指数m对固结速率有明显影响,在固结初期,m越大,固结速率越快;而在固结后期,m越大,固结速率越慢。其原因为在固结初期,水力坡度较大(大于1),则m越大,考虑指数渗流模式的固结速率越快,因此,当m>1时其固结速率快于达西渗流,当m<1时,其固结速率小于达西渗流;在固结后期,水力梯度较小(小于1),情况则相反,因此,当m>1时,其固结速率小于达西渗流速率,当m<1时,其固结速率大于达西渗流速率。此外,当m=1.2和1.5时,与达西渗流的性况(m=1)固结速率最大差异分别为17.94%和25.73%。
图4所示为m=1.5时真空荷载p0对固结速率的影响曲线。由图4可知:p0越大,即真空压力比VPR越大,固结速率越快。对比工况6中真空荷载 p0=0即未进行真空预压,工况7固结速率最大可提高6.82%。
图5和6所示分别为涂抹区半径和竖井半径之比s对固结度的影响和κh/κs对固结度的影响。图5和图6则反映了涂抹作用对固结速率的影响十分显著。涂抹区范围参数,即半径和竖井半径之比s越大,固结速率越慢,工况5和工况12速率相差最大值为14.36%;涂抹区与未扰动区渗透系数之比κh/κs越大,即涂抹区渗透系数减小得越多,固结速率也随之越慢,工况5和工况15速率相差最大值为15.19%。
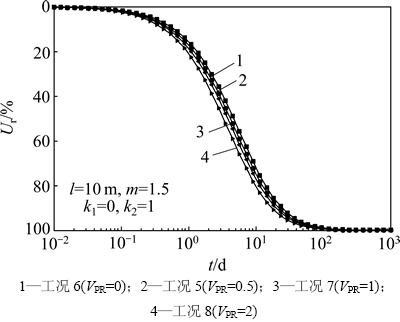
图4 m=1.5时真空压力比V PR(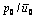 )对固结度的影响
)对固结度的影响
Fig.4 Influence of VPR on consolidation rate when m=1.5
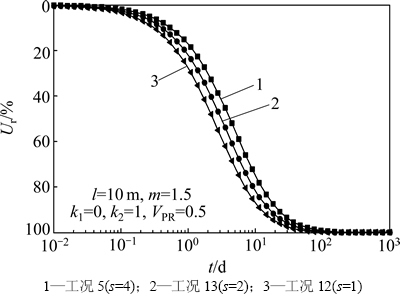
图5 m=1.5时涂抹区半径和竖井半径之比s对固结度的影响
Fig. 5 Influence of s on consolidation rate when m=1.5
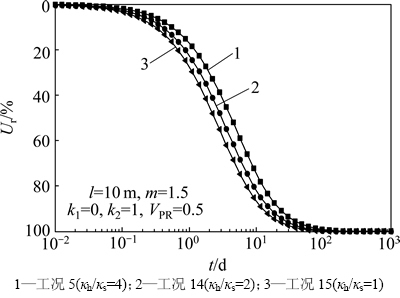
图6 m=1.5时κh/κs对固结度的影响
Fig. 6 Influence of κh/κs on consolidation rate when m=1.5
图7所示为衰减系数kl和k2对固结速率的影响曲线,其值为0即表明三角形衰减,其值为1.0则表明不衰减。其中,kl=0,k2=1的情况最接近实际负压分布情况。由图7中可知:衰减系数越小,则固结速率越慢。
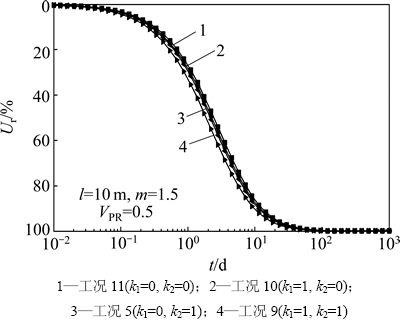
图7 m=1.5时衰减系数k1和k2对固结度的影响
Fig. 7 Influence of kl and k2 on consolidation rate when m=1.5
5 结论
1) 非达西渗流指数m对固结速率影响最为显著:在固结初期,随着m的增大,固结速率会明显加快,在固结后期则反之。
2) 涂抹作用会极大地减慢土体固结速率,因而,在施工中应当避免对土体扰动,如注意地基的降排水,避免排水板间距过小。
3) 考虑非达西渗流对固结度计算有较大的影响,因此,在实际工程中进行预测分析时,引入非达西渗流理论有可能获得与实际更接近的结果。
参考文献:
[1] Hansbo S. Consolidation of clay with special reference to influence of vertical drains[C]// Swedish Geotechnical Institute Proceeding. Stockholm: Swedish Geotechnical Institute, 1960, 18: 45-50.
[2] Miller R J, Low P E. Threshold gradient for water flow in clay systems[J]. Soil Science Society of American Journal, 1963, 27(6): 605-609.
[3] Slepicka F. Contribution to the solution of the filtration law[C]// International union of Geodesy and Geophysics, Commission of Subterranean Waters. Finland, 1960: 245-258.
[4] 刘忠玉, 刘忠广, 马崇武. 考虑起始水力梯度时饱和黏土的一维固结[J]. 郑州大学学报(工学版), 2006, 27(3): 21-24.
LIU Zhongyu, LIU Zhongguang, MA Chongwu. One-dimensional consolidation of saturated clays considering initial hydraulic gradient[J]. Journal of Zhengzhou University (Engineering Science), 2006, 27(3): 21-24.
[5] 刘忠玉, 孙丽云, 乐金朝, 等. 基于非Darcy渗流的饱和黏土一维固结理论[J]. 岩石力学与工程学报, 2009, 28(5): 973-979.
LIU Zhongyu, SUN Liyun, YUE Jinchao, et al. One-dimensional consolidation theory of saturated clay based on non-Darcy flow[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(5): 973-979.
[6] XIE Kanghe, WANG Kun, WANG Yulin, et al. Analytical solution for one-dimensional consolidation of clayey soils with a threshold gradient[J]. Computers and Geotechnics, 2010, 37(4): 487-493.
[7] 王坤, 谢康和, 刘兴旺, 等. 初始孔压非均布考虑起始比降的一维固结解[J]. 岩土工程学报, 2011, 33(9): 1419-1424.
WANG Kun, XIE Kanghe, LIU Xingwang, et al. Solution for one-dimensional consolidation with threshold gradient subjected to non-uniformly distributed initial pore water pressure[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(9): 1419-1424.
[8] 李传勋, 谢康和, 王坤, 等. 基于指数形式渗流定律的软土一维固结分析[J]. 土木工程学报, 2011, 44(8): 111-118.
LI Chuanxun, XIE Kanghe, WANG Kun, et al. One-dimensional consolidation analysis considering exponential flow law for soft clays[J]. China Civil Engineering Journal, 2011, 44(8): 111-118.
[9] Teh C I, Nie X Y. Coupled consolidation theory with non-Darcian flow[J]. Computers and Geotechnics, 2002, 29(3): 169-209.
[10] 邓岳保, 谢康和, 李传勋. 考虑非达西渗流的比奥固结有限元分析[J]. 岩土工程学报, 2012, 34(11): 2058-2065.
DENG Yuebao, XIE Kanghe, LI Chuanxun, et al. Finite element analysis of Biot’s consolidation with non-Darcian flow[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2058-2065.
[11] Hansbo S. Consolidation equation valid for both Darcian and non-Darcian flow[J]. Géotechnique, 2001, 51(1): 51-54.
[12] Walker R, Indraratna B, Rujikiatkamjorn C. Vertical drain consolidation with non-Darcy flow and void-ratio-dependent compressibility and permeability[J]. Geotechnique, 2012, 62(11): 985-997.
[13] 董志良. 堆载及真空预压砂井地基固结解析理论[J]. 水运工程, 1992(9): 1-7.
DONG Zhiliang. Analytical consolidation theory of sand drain ground under preloading with vacuum preloading[J]. Port and Waterway Engineering, 1992(9): 1-7.
[14] Indraratna B, Rujiliatkamjorn C, Athananthan L, et al. Analytical and numerical modeling of soft soil stabilized by prefabricated vertical drains incorporating vacuum preloading[J]. International Journal of Geomechanics, 2005, 5(2):114-124.
[15] Rujiliatkamjorn C, Indraratna B. Analytical solutions and design curves for vacuum-assisted consolidation with both vertical and horizontal drainage[J]. Canadian Geotechnical Journal, 2007, 44(2): 188-200.
(编辑 陈爱华)
收稿日期:2014-05-22;修回日期:2014-07-28
基金项目(Foundation item):国家自然科学基金资助项目(51179170) (Project(51179170) supported by the National Natural Science Foundation of China)
通信作者:谢康和,教授,博士生导师,从事软土固结与变形控制理论研究;E-mail: zdkhxie@zju.edu.cn