DOI: 10.11817/j.issn.1672-7207.2015.03.012
薄壳工件的动力学特性对切削稳定性的影响
孙伟1,张洪浩2,汪博1,郝春磊1
(1. 东北大学 机械工程与自动化学院,辽宁 沈阳,110819;
2. 华晨汽车工程研究院,辽宁 沈阳,110141)
摘要:研究提出同时考虑薄壳工件及主轴-刀具系统柔性进行切削稳定性预测的方法。分析包含工件动力学特性预测切削稳定性的原理,推导稳定性预测公式。提出考虑工件动力学特性预测切削稳定性的分析流程。以切削薄板类工件为例,采用本文所提出的方法进行实例研究,并分析系统的阻尼、工件的材料参数对切削稳定性的影响规律。
关键词:薄壳工件;动力学特性;切削颤振;稳定性预测;影响分析
中图分类号:TG502.14;TH113.1 文献标志码:A 文章编号:1672-7207(2015)03-0849-07
Effects of dynamic characteristics of thin-walled workpieces on machining stability
SUN Wei1, ZHANG Honghao2, WANG bo1, HAO Chunlei1
(1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Brilliance Auto R&D Center, Shenyang 110141, China)
Abstract: A method for predicting machining stability, considering both the thin-walled workpiece and spindle-tool system, was presented. The theory containing the dynamic characteristics of workpiece for stability prediction was analyzed, the stability prediction formula was deduced, and the analysis procedure was provided. Taking a thin plate workpiece as study object, the proposed method was demonstrated. And the effects of the system damping and material parameters of workpiece on the machining stability were analyzed.
Key words: thin-walled workpieces; dynamic characteristic; machining chatter; stability prediction; analysis of effect
在航空、航天、汽车等工业中,需要加工大量的薄壳工件,例如,各种壳体件、套筒件、环形件、盘形件、平板件等。在加工薄壳工件时,通常需要从母材中移除大量的材料,导致工件的刚度降低、强度减弱,造成薄壳构件在加工过程中出现振动超标,这是最常见的零件加工失效模式。更有甚者,在高速切削时,将导致切削刀具和工件之间发生剧烈的自激振动,即颤振。颤振将导致工件的表面加工质量恶化,在工件表面留下振纹,同时还可能导致主轴、刀具发生损坏,降低机床的寿命[1-2]。为了得到较好的加工效率同时又避免发生颤振,需要合理配置主轴转速、切削深度、进给量等特性参数,即开展切削稳定性预测以及优化切削工艺的研究。长期以来,学者们进行了大量的关于切削颤振分析以及预测的研究[3-5],其中最普遍的是利用测试或分析获得的主轴-刀具系统刀尖点的频响函数,绘制稳定叶瓣图来评价切削稳定性[6-7],进一步选择不发生颤振的切削条件。对于刚性较好的工件,这种预测方式是有效的。但是,对于本文作者所研究的薄壳工件,单纯考虑主轴系统的柔性,将会产生很大的预测误差。本文作者提出同时考虑薄壳工件及主轴系统的柔性进行切削稳定性预测的方法。首先分析了考虑工件动力学特性预测切削稳定性的原理,推导了稳定性预测公式。进一步提出了考虑工件动力学特性预测切削稳定性的分析流程。最后,以切削薄板类工件为例,采用本文所提出的方法进行了实例研究。
1 包含工件动力学特性的预测切削稳定性的原理
柔性主轴系统切削薄壳工件,可用图1所示的单自由度系统模型来描述,主要包括了主轴-刀具系统和工件系统在垂直于刀具进给方向产生的振动。图中P为切削点; 和
和 分别为主轴-刀具系统和工件系统的振动响应;
分别为主轴-刀具系统和工件系统的振动响应; 和
和 分别为切削点处工件与刀具所受的动态切削力(这2个力大小相等、方向相反);h0为理论切削厚度;h为动态切削厚度。则主轴-刀具系统和工件系统的运动方程可分别表达为
分别为切削点处工件与刀具所受的动态切削力(这2个力大小相等、方向相反);h0为理论切削厚度;h为动态切削厚度。则主轴-刀具系统和工件系统的运动方程可分别表达为
 (1)
(1)
 (2)
(2)
式中:MT和MW分别为主轴-刀具系统和工件系统的等效质量;KT和KW分别为主轴-刀具系统和工件系统的刚度;CT和CW分别为主轴-刀具系统和工件系统的等效阻尼;DT为主轴旋转产生的陀螺效应系数。
工件与刀具之间产生的动态切削力与切削深度和厚度等因素相关,可进一步表示为[8]
 (3)
(3)
式中:Kt为进给方向的切削力系数;ap为切削深度;h(t)为动态切削厚度。

图1 单自由度动力学切削模型
Fig. 1 Dynamic cutting model
在这个耦合系统中,假设工件表面切削点处当前的振动为 ,上一个周期的振动为
,上一个周期的振动为 ,其中,
,其中, 为主轴旋转周期,参照文献[9],则动态切削厚度h可表示为
为主轴旋转周期,参照文献[9],则动态切削厚度h可表示为
 (4)
(4)
将方程(4)由时域变换为拉氏域,可表示为
 (5)
(5)
类似的也可将方程(1)和方程(2)变换到拉氏域,表达为
 (6)
(6)

 (7)
(7)
则
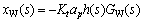 (8)
(8)
 (9)
(9)
其中:GW(s)和GT(s)为工件和主轴-刀具系统在拉氏域内的传递函数,表达式为
 (10)
(10)
 (11)
(11)
将式(8)和(9)代入到式(5)得
 (12)
(12)
整理得动态切削厚度和理论切削厚度之间的传递函数

 (13)
(13)
耦合系统的特征方程为
 (14)
(14)
式中:G(s)为切削点处耦合系统的传递函数,表达为
 (15)
(15)
式(13)的稳定性取决于特征方程(14)的特征根s的性质,s可以写成 的形式。当
的形式。当 时,系统处于临界稳定状态,工件以颤振频率
时,系统处于临界稳定状态,工件以颤振频率 和恒定的振幅振荡,则特征方程变为
和恒定的振幅振荡,则特征方程变为
 (16)
(16)
其中:aplim为无颤振加工的最大切削深度; 为频域内的系统传递函数,也称为频响函数。
为频域内的系统传递函数,也称为频响函数。
由于频响函数是复数,可以表示为
 (17)
(17)
最大切削深度aplim为实数,所以虚部为0,最终得到无颤振条件下极限切深的表达式为
 (18)
(18)
式中:N为刀齿数。无颤振切削条件为:ap<aplim。
2 考虑工件动力学特性的预测切削稳定性的流程
2.1 预测流程
由式(18)可知:切削薄壳工件的主轴系统,其切削稳定性是由主轴系统与工件系统的动力学特性共同决定的。因而,对于这一耦合系统,预测切削稳定性可参照以下4个关键步骤。
1) 主轴系统刀尖点频响函数预测。机床主轴系统是由主轴、刀柄、刀具组成的一个复杂的动力学系统。要想获得刀尖点的频响函数,需要创建主轴系统的动力学分析模型。许多学者在建立主轴系统动力学模型方面进行了长期的探索,相关建模方法共包括以下3种:阻抗耦合子结构法[10-11]、有限元法[12-13]、解析法[14]等。其中,有限元法是最常用的创建主轴系统动力学分析的方法,具体建模过程可概括为,用梁单元模拟主轴、刀柄、刀具等机械本体,用弹簧单元模拟轴承支撑以及主轴-刀柄-刀具之间的结合面,从而构件出用于分析求解的有限元方程[15]。利用主轴系统的有限元方程可以预测刀尖点的频响函数。
2) 工件切削点处频响函数预测。预测工件切削点处的频响函数同样需要创建工件系统的动力学分析模型。相对于主轴系统,创建工件系统的分析模型较为容易,同样可以通过有限元法来实现。但是,为了考核不同切削位置处的切削稳定性,需要求解若干指定位置处的频响函数。例如,图2所示的曲面薄壳工件,需要计算图中所示7个关键位置处切削点的频响函数。

图2 刀具切削曲面薄壳工件
Fig. 2 Schematic diagram of cutting surface of thin-walled workpiece.
3) 2个子系统之间频响函数的耦合。将获得的主轴系统刀尖点频响函数和工件切削点处的频响函数进行相加,则可获得耦合系统的刀尖点频响函数。根据式(17)将耦合系统频响函数分解成实部 与虚部
与虚部 的形式。获得的频响函数用于后续的切削稳定性预测。
的形式。获得的频响函数用于后续的切削稳定性预测。
4) 绘制切削稳定性叶瓣图。进一步获得工件、刀具的切削力系数和材料参数,输入上一步求得的频响函数,则可绘制用于描述切削稳定性的叶瓣图。
2.2 切削稳定性叶瓣图的绘制方法
绘制切削稳定性叶瓣图可参照如下4个步骤。
1) 由频响函数获得颤振频率 及其对应的
及其对应的 和
和 。轴向切削深度aplim为物理量,必须为正值,由式(18)可知:只有频响函数实部为负值时,aplim才具有物理意义。在指定的频率范围内(由主轴的最大的转速确定),根据主轴-刀具-工件耦合系统切削点处的频响函数,选择所有满足上述条件的颤振频率
。轴向切削深度aplim为物理量,必须为正值,由式(18)可知:只有频响函数实部为负值时,aplim才具有物理意义。在指定的频率范围内(由主轴的最大的转速确定),根据主轴-刀具-工件耦合系统切削点处的频响函数,选择所有满足上述条件的颤振频率 及与其对应的
及与其对应的 和
和 。
。
2) 计算最大切削深度aplim。确定aplim是为了得到最大化的材料去除率,将已求得的 和已知的刀具齿数N、切削力系数Kt代入式(18),得到与颤振频率
和已知的刀具齿数N、切削力系数Kt代入式(18),得到与颤振频率 一一对应的切削深度。
一一对应的切削深度。
3) 计算主轴转速n。定义在颤振频率 处的变量
处的变量 为
为
 (19)
(19)
则结构传递函数的相移为
 (20)
(20)
当前刀齿与前一个刀齿的振痕的相移 为
为
 (21)
(21)
如果设k是与振动引起的留在工件表面振动波纹数相对应的整数,即稳定性图中的叶瓣数,那么
 (22)
(22)
则主轴旋转周期为
 (23)
(23)
根据主轴转速的定义:
 (24)
(24)
将式(23)代入式(24)中,可以得到主轴转速的表达式:
 (25)
(25)
由式(25)计算叶瓣k=0, 1, 2, 3, …时的主轴转速。
4) 绘制稳定性叶瓣图。以上3个步骤计算完毕后,便可绘制出以主轴转速n为横坐标,以极限轴向切削深度aplim为纵坐标的平面稳定性叶瓣图。
3 薄壳工件的动力学特性对切削稳定性的影响
3.1 主轴-刀具和工件系统的有限元建模
以下以切削薄板件为例,分析主轴-刀具-工件耦合系统的切削稳定性。其中主轴系统的有限元模型见图3,采用梁单元模拟主轴、刀柄和刀具,共划分了27个主轴轴段,3个刀具轴段、4个刀柄轴段,各轴段尺寸见表1和2。轴承采用弹簧单元来模拟,具体参数见表3。设主轴、刀柄和刀具材料相同,弹性模量E=207.8 GPa,密度ρ=7.806 t/m3,泊松比μ=0.3。选取刀具齿数为4,切削力系数Kt=3 GPa,系统的阻尼比为0.03。

图3 主轴系统有限元模型
Fig. 3 Finite element model of spindle system
表1 主轴轴段尺寸
Table 1 Sizes of shaft sections

表2 刀具和刀柄轴段尺寸
Table 2 Shaft section sizes of tool and holder

表3 轴承的位置及支撑刚度
Table 3 Position and supporting stiffness of bearings

工件为铝合金材料,弹性模量EW=70 GPa,密度为 =2.7 t/m3,泊松比
=2.7 t/m3,泊松比 =0.288,工件长×宽×高为100 mm×80 mm×4 mm。利用ANSYS软件,选用SOLID185单元建立工件的有限元模型,如图4所示。其中共有 240个单元,396个节点。采用底面全约束的约束方式可以使薄壳工件更加接近真实的切削环境,图中圆点加箭头的标记为切削点。
=0.288,工件长×宽×高为100 mm×80 mm×4 mm。利用ANSYS软件,选用SOLID185单元建立工件的有限元模型,如图4所示。其中共有 240个单元,396个节点。采用底面全约束的约束方式可以使薄壳工件更加接近真实的切削环境,图中圆点加箭头的标记为切削点。

图4 薄壳工件有限元模型
Fig. 4 Finite element model of thin-walled workpiece
3.2 考虑薄壳工件动力学特性的主轴系统切削稳定性预测
按照3.1节部分所创建的模型,假设刀具处于位置1时,计算主轴系统的切削稳定性。分别计算主 轴-刀具系统刀尖处、工件系统在位置1处以及主轴-刀具-工件耦合系统在切削位置处的频响函数,相应的结果列在图5中。从图5可以看出:由主轴-刀具系统和工件系统,计算出的频响函数有很大的不同,因而单独依赖于任何系统,均无法科学地预测其削稳定性。对于切削薄壳工件的主轴系统,必须将上述两个系统耦合在一起,进而计算切削稳定性。
图6所示为对应于图5中3种情况,所计算的切削稳定性。从图6可以看出:对于本文所研究的切削薄壳工件主轴系统,工件系统的动力学特性对切削稳定性有着重要的影响。
考虑到切削位置点的移动,对于所研究的系统,只有用三维稳定性叶瓣图才能充分描述切削薄壳工件的稳定性。图7所示为对应于图4所表示的7个位置所绘制的三维稳定性叶瓣图。

图5 不同情况计算获得的频响函数
Fig. 5 FRFS for different situations

图6 不同情况计算获得的稳定性叶瓣图
Fig. 6 Stability lobes diagrams for different situations

图7 不同位置的三维稳定图
Fig. 7 3D stability lobes diagram for different tool–workpiece positions
3.3 特性参数对切削稳定性的影响
1) 阻尼对切削稳定性的影响。为了分析阻尼对切削稳定性的影响,保持其他参数不变,给定系统的阻尼比分别为0.015,0.03和0.06,考核阻尼对切削稳定性的影响。对应于上述3种阻尼,所求得的稳定叶瓣图见图8。从图8可以看出:随着阻尼比的增大,极限切深也增大,稳定区(叶瓣图下方区域)的范围变大,但叶瓣峰值变化不大。
2) 工件弹性模量对切削稳定性的影响。选取铝合金、钛合金及碳钢这3种常用材料进行分析,弹性模量分别为70,107.8和206 GPa。分析工件的弹性模量对切削稳定性的影响,相关结果见图9。由图9可以看出:随着弹性模量的增大(工件刚度的增大),极限切削深度不断增大,稳定区域也随之增大。
3) 工件密度对切削稳定性的影响。同样选取铝合金、钛合金及碳钢3种材料,密度值分别为2.7,4.5和7.85 t/m3,计算工件密度对切削稳定性的影响,相关结果见图10。从图10可以看出:随着密度的增大,极限切削深度变大(叶瓣图整体向上移动),同时向转速低的方向移动。

图8 阻尼对稳定图的影响
Fig. 8 Effects of damping on stability lobes diagram

图9 弹性模量对稳定图的影响
Fig. 9 Effects of elastic modulus on stability lobes diagram

图10 密度对稳定图的影响
Fig. 10 Effects of density on stability lobes diagram
4 结论
1) 基于单自由切削动力学模型,推导了包含工件动力学特性的预测切削稳定性的原理性公式。
2) 提出了考虑工件动力学特性预测切削稳定性的分析流程,具体包括:主轴系统刀尖点频响函数预测、工件切削点处频响函数预测、2个子系统之间频响函数的耦合、绘制切削稳定性叶瓣图等关键步骤。
3) 以切削薄板类工件为例,采用本文所提出的方法进行了实例研究,并分析系统的阻尼、工件的材料参数对切削稳定性的影响规律。随着阻尼比的增大,极限切深增大,稳定区的范围变大;随着工件弹性模量的增大(工件刚度的增大),极限切削深度不断增大,稳定区域也随之增大;随着工件密度的增大,极限切削深度变大(叶瓣图整体向上移动),同时向转速低的方向移动。
参考文献:
[1] Arnaud L, Gonzalo O, Seguy S, et al. Simulation of low rigidity part machining applied to thin-walled structures[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(5/6/7/8): 479-488.
[2] Thevenot V, Arnaud L, Dessein G, et al. Integration of dynamic behaviour variations in the stability lobes method: 3D lobes construction and application to thin-walled structure milling[J]. The International Journal of Advanced Manufacturing Technology , 2006, 27(7/8): 638-644.
[3] Alan S, Budak E,  H N. Analytical prediction of part dynamics for machining stability analysis[J]. International Journal of Automation Technology, 2010, 4(3): 259-267.
H N. Analytical prediction of part dynamics for machining stability analysis[J]. International Journal of Automation Technology, 2010, 4(3): 259-267.
[4] Bravo U, Altuzarra O, López de Lacalle L N, et al. Stability limits of milling considering the flexibility of the workpiece and the machine[J]. International Journal of Machine Tools and Manufacture, 2005, 45(15): 1669-1680.
[5] Budak E,  L T, Alan S, et al. Prediction of workpiece dynamics and its effects on chatter stability in milling[J]. CIRP Annals-Manufacturing Technology, 2012 , 61(1): 339-342.
L T, Alan S, et al. Prediction of workpiece dynamics and its effects on chatter stability in milling[J]. CIRP Annals-Manufacturing Technology, 2012 , 61(1): 339-342.
[6]  Y, Budak E. Analytical prediction of stability lobes in milling[J]. CIRP Annals-Manufacturing Technology, 1995, 44(1): 357-362.
Y, Budak E. Analytical prediction of stability lobes in milling[J]. CIRP Annals-Manufacturing Technology, 1995, 44(1): 357-362.
[7] Gagnol V, Bouzgarrou B C, Ray P, et al. Model-based chatter stability prediction for high-speed spindles[J]. International Journal of Machine Tools and Manufacture, 2007, 47(7): 1176-1186.
[8] 梁睿君, 叶文华. 薄壁零件高速铣削稳定性预测与验证[J]. 机械工程学报, 2009, 45(11): 146-151.
LIANG Ruijun, YE Wenhua. Stability Prediction for high-speed milling of thin walled structures and experimental validation[J]. Journal Of Mechanical Engineering, 2009, 45(11): 146-151.
[9] Cardi A A, Firpi H A, Bement M T, et al. Workpiece dynamic analysis and prediction during chatter of turning process[J]. Mechanical Systems and Signal Processing, 2008, 22(6): 1481-1494.
[10] Schmitz T L, Donalson R R. Predicting high-speed machining dynamics by substructure analysis[J]. CIRP Annals- Manufacturing Technology, 2000, 49(1): 303-308.
[11] Ahmadi K, Ahmadian H. Modeling machine tool dynamics using a distributed parameter tool-holder joint interface[J]. International Journal of Machine Tools and Manufacture, 2007, 47(12): 1916-1928.
[12] Kang Y, Chang Y P, Tsai J W, et al. Integrated ‘CAE’ strategies for the design of machine tool spindle-bearing systems[J]. Finite Elements in Analysis and Design, 2001, 37(6): 485-511.
[13] Rantatalo M,  , et al. Milling machine spindle analysis using FEM and non-contact spindle excitation and response measurement[J]. International Journal of Machine Tools and Manufacture, 2007, 47(7): 1034-1045.
, et al. Milling machine spindle analysis using FEM and non-contact spindle excitation and response measurement[J]. International Journal of Machine Tools and Manufacture, 2007, 47(7): 1034-1045.
[14] Gao S H, Long X H, Meng G. Nonlinear response and nonsmooth bifurcations of an unbalanced machine-tool spindle-bearing system[J]. Nonlinear Dynamics, 2008, 54(4): 365-377.
[15] 汪博, 孙伟, 闻邦椿. 考虑主轴-刀柄-刀具结合面的高速主轴系统动力学特性有限元建模[J]. 机械工程学报, 2012, 48(15): 83-89.
WANG Bo, SUN Wei, WEN Bangchun. The finite element modeling of high-speed spindle system dynamics with spindle-holder-tool joints[J]. Journal of Mechanical Engineering, 2012, 48(15): 83-89.
(编辑 陈爱华)
收稿日期:2014-04-09;修回日期:2014-06-27
基金项目(Foundation item):国家自然科学基金资助项目(50905029) (Project (50905029) supported by the National Natural Science Foundation of China)
通信作者:孙伟,博士,副教授,从事机械系统动力学及振动控制研究;E-mail: weisun@me.neu.edu.cn