层状岩体边坡抗滑桩加固效应的数值分析
徐爱民1, 2,柳群义2, 3,朱自强2,鲁光银2
(1. 湖南省高速公路管理局 湖南 长沙,410003;
2. 中南大学 地球科学与信息物理学院 湖南 长沙,410083;
3. 中国地质科学院 矿产资源研究所,北京,100037)
摘要:利用数值方法探讨抗滑桩在层状岩体边坡中的加固效果,分析抗滑桩位置和桩长对于边坡变形、应力的影响。研究结果表明:抗滑桩位置对于边坡水平位移的影响较大;当抗滑桩位于边坡坡面中下部时(但需保证抗滑桩穿过了最危险滑动面),对岩土体变形的效果最佳;随着桩长的增大,边坡水平位移突变逐渐减少,最大位移也逐渐减小。存在一临界桩长Lcr,当桩长超过Lcr时,继续增大桩长对位移的控制效果明显降低。
关键词:层状岩体;边坡;抗滑桩;加固效应;应力;变形;数值分析
中图分类号:TU457 文献标志码:A 文章编号:1672-7207(2011)08-2453-06
Numerical analysis for reinforcement response of pile in stratified rock slope
XU Ai-min1, 2, LIU Qun-yi2, 3, ZHU Zi-qiang2, LU Guang-yin2
(1. Hunan Expressway Authority, Changsha 410003, China;
2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
3. Institute of Mineral Resources, Chinese Academy of Geological Sciences, Beijing 100037, China)
Abstract: The reinforcement effect of the pile in rock bedded slope was studied by the numerical analysis method. The effects of the pile location, pile length to the deformation and stress of slope were analyzed. The results show that the location of pile has great influences on the horizontal displacement of slope. If the pile is driven at the mid-bottom place of slope surface and makes sure that the pile is driven through the potential slip surface, the effect of controlling deformation of rock mass is the best. With the increase of the length of pile, the maximum displacement of slope is decreased gradually. There exists a limit pile length Lcr, if pile length is larger than Lcr, and the effect of pile length on deformation control will reduce.
Key words: stratified rock mass; slope; pile; reinforcement effect; stress; deformation; numerical analysis
抗滑桩在边坡加固工程中广泛使用,许多研究者对此进行了大量研究[1-4],但他们主要采用极限平衡法研究边坡稳定性以及抗滑桩受力情况,该方法需对桩土受力以及边坡滑动面进行假设,无法清晰反映边 坡-抗滑桩的耦合效应以及边坡的滑移特征,并且由于桩和岩土介质具有不同的弹性模量、重度和强度,势必引起应力分布的非均匀化和进入塑性极限的不同步,给边坡的稳定分析带来了较大的困难[5]。近年来,随着计算机技术的不断发展,数值方法在岩土工程分析中逐渐得到广泛应用[6-9],该法不受岩土体几何形状不规则和材料不均匀性的限制,如Jeong等[10]利用极限平衡法和有限差分软件FLAC3D 分析了边坡-抗滑桩系统的稳定性。但是,这些研究对象主要是针对土质边坡或者不含结构面的岩体边坡,对于层状岩体中抗滑桩加固效果的研究较少,在此,本文作者利用FLAC3D数值计算方法,探讨层状岩体边坡抗滑桩的加固效应,分析抗滑桩位置和桩长对于边坡变形和应力的影响。
1 桩-岩相互作用特征
桩单元包括3个弹簧单元,其中2个弹簧单元平行于桩轴线以提供轴力和轴向剪力,另一个垂直于轴线以提供横向抗力,如图1所示。桩单元被分为许多小段,通过这些小段的积分得到桩整体的变形和应力状态[11]。
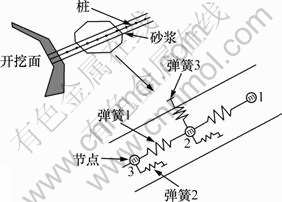
图1 桩力学模型
Fig.1 Mechanical model of pile
1.1 桩的轴力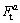
桩单元的轴向力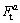 可由其轴向位移ubt得到:
可由其轴向位移ubt得到:
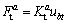 (1)
(1)
式中: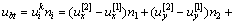
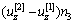 ;
; 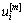 为桩单元m节点在i方向上的位移;ni为桩轴线的方向余弦。
为桩单元m节点在i方向上的位移;ni为桩轴线的方向余弦。
1.2 桩的轴向摩擦力
桩-岩之间的剪切行为如图2所示。当桩-砂浆、砂浆-岩石界面发生剪切滑移后,利用桩单元法向平均有效围压σm、砂浆的黏结强度cg、砂浆的剪切刚度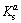 、砂浆的内摩擦角
、砂浆的内摩擦角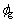 、砂浆的外周长pg,可得到相应的力学性质。σm根据下式得到:
、砂浆的外周长pg,可得到相应的力学性质。σm根据下式得到:
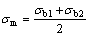 (2)
(2)
式中:σb1和σb2为桩轴线的法平面应力。
假设相应接触面符合Mohr-Coulomb破坏模型,桩的轴向剪力可表示为:
 (3)
(3)
式中:Fs为砂浆体内产生的剪切力;ubs为桩和岩土界面之间的相对位移;l为桩长。
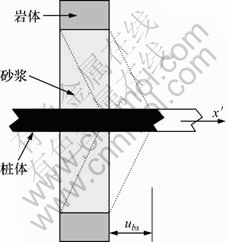
图2 桩变形模型
Fig.2 Deformation model of pile
砂浆所能承受的最大剪力为:
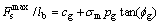 (4)
(4)
桩的横向抗剪能力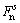 为:
为:
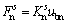 (5)
(5)
式中: 为桩的横向剪切刚度;ubn为桩的横向位移。
为桩的横向剪切刚度;ubn为桩的横向位移。
2 数值计算模型
2.1 数值计算模型
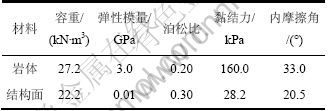
层状岩体边坡的数值分析模型如图3所示。对于结构面的模拟,采用低强度弹塑性夹层单元,结构面倾角为40°,厚度为0.1 m,结构面之间的间距为10 m;结构面以外的岩石视为均质体。模型共36 253个单 元,11 977个节点,自然坡角为10?,开挖后形成的边坡高为45 m,坡角为75?。弹塑性准则采用Mohr-Coulomb模型,该模型包含剪切和拉伸2个准则。根据层状岩体的工程地质特性,选择适当的计算参数,见表1。桩单元直径为2.0 m,弹性模量为200.0 GPa。根据文献[12],设置桩和岩体的黏结力和内摩擦角与所接触的岩体相同,二者的切向刚度和法向刚度均为1.3×1011 N/m。计算收敛准则为:不平衡力比率满足10-5。模型整体边界条件为:下部固定约束,左、右两侧水平约束,上部为自由边界。
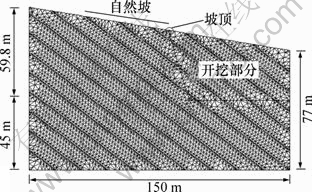
图3 数值模拟模型
Fig.3 Numerical simulation model
表1 计算参数
Table 1 Calculation parameters
2.2 数值监测点布置
边坡的开挖将使岩体产生位移扰动。这种扰动是一个非线性的力学过程。扰动结束后,若边坡仍处于平衡状态,则各个部位的位移将趋于稳定;为了揭示各个部位岩体的变形情况,在边坡体中布置若干监测点,具体布置方式为:沿坡顶向下每隔5 m设1个监测点,共10个监测点,分别标记为P01~P10,然后,以这些监测点为起点,向坡体内侧布置其他监测点,从而形成监测线,监测线上的监测点之间间距为2 m,每条监测线共26个记录点,如图4所示。
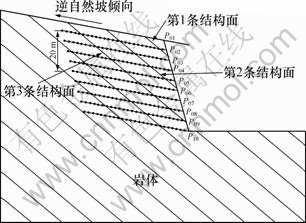
图4 监测点位置
Fig.4 Monitoring points location
3 数值计算结果与讨论
计算边坡在无抗滑桩加固情况下的位移和应力,结果见图5。从图5可见:当边坡中无桩加固时,边坡的水平位移较大,最大水平位移位于第3条结构面的下缘,说明该处为潜在滑动面的位置,较危险,需对该处进行重点加固。

图5 未设置抗滑桩时边坡的响应
Fig.5 Response of slope without pile reinforcement
3.1 抗滑桩位置的影响
3.1.1 水平位移
为了分析抗滑桩在不同位置打入情况下,边坡岩土体的应力变形响应,分别在边坡的6个位置打入抗滑桩(见图6,其中位置1和2的水平距离为h/4,h为边坡的高度),得到相应的水平位移,如图7所示。从图7可以看出:边坡的最大水平位移仍发生在第3条结构面的下缘;随着抗滑桩设置位置的下移(除了坡脚处),边坡的水平位移逐渐减小,对应位置1,3和5,最大水平位移分别为86.1,65.1和52.4 mm。可见:抗滑桩设置的位置对于边坡的水平位移影响较大,当抗滑桩设置于边坡坡面的中下部时(但需保证抗滑桩穿过了最危险滑动面),对于岩土体变形的效果最佳。抗滑桩设置在坡脚时,边坡的最大水平位移为130.0 mm。这是由于最危险滑动面位于第3条结构面处,而坡脚设置抗滑桩并不能通过第3条结构面,无法对其进行最佳加固;但与未设置抗滑桩相比,边坡的最大位移为374.4 mm。可见:尽管抗滑桩位于潜在滑动面以下,但边坡的变形仍然得到一定加固。这是由于抗滑桩加入边坡后,岩土体的性质发生改变,以有效地将边坡滑动体和下部稳定岩体牢固地拉结成一体,在开挖后,边坡的应力和变形情况得到改善,从而限制了上部滑动体沿结构面的变形移动。从图7还可看出:在未设置抗滑桩、抗滑桩设置在自然坡、抗滑桩设置在坡脚等情况下,边坡岩土体的位移云图变化梯度较大,在第3条结构面两侧位移存在较大差异;当抗滑桩设置边坡中间时,边坡的位移云图较均匀,无明显的变形阶跃现象。
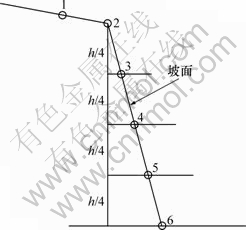
图6 抗滑桩位置示意图
Fig.6 Pile locations
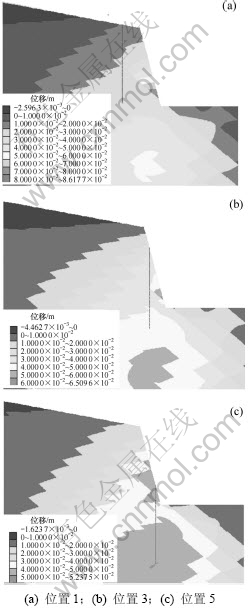
图7 不同抗滑桩位置下的水平位移云图
Fig.7 Horizontal displacement contour of slope with different pile locations
图8所示为抗滑桩加固边坡后,岩土体监测点的水平位移。从图8可以看出:当抗滑桩位于自然坡或边坡坡面上时,监测点从上到下的位移曲线沿自然坡的变化趋势从均匀变化过渡到尖点突变变化形态,尖点突变形态发生在监测点P09处,说明该点稳定性较弱。对比P09点在边坡体中的位置可以看出:其位于第3条结构面处;而其他监测线上的位移变化均较均匀;当抗滑桩设置在坡脚时,水平位移监测曲线呈现出多个台阶的形态。这是由于此时监测线经过结构面,位移传递收到阻隔。各监测点位移沿自然坡倾向位置逐渐减小,说明越往岩体内部,受到的开挖扰动越小,边坡的水平位移也越小,与实际情况较相符[11]。
3.1.2 剪应力
通过FLAC3D数值计算,得到边坡岩体剪应力分布如图9所示。从图9可见:天然层状岩体边坡开挖后,岩体边界条件发生变化,导致原岩应力场重新分布。由于岩体开挖的卸荷作用,解除了坡面右侧的约束,导致结构面上剪应力增大,同时产生一部分拉应力以及平行于结构面的卸荷裂隙,这些卸荷裂隙削弱了结构面的抗剪切强度,是层状边坡滑动失稳的影响因素之一;另外,由于结构面上的剪应力增大,使得结构面的下部受到挤压,从而引起坡脚处产生了应力集中现象,未设置抗滑桩时坡脚处的最大剪应力为1.229 MPa,随着抗滑桩设置位置的下移,坡脚处的最大剪应力分别为(对应1,3和5位置)1.248,1.375和1.631 MPa。可见:抗滑桩设置在坡脚时改变了此处岩土体的应力,明显减小了应力集中现象。
3.2 抗滑桩桩长的影响
通过分析桩位置对于边坡体水平位移的影响可知:在位置5(图9(c))处设置抗滑桩对于边坡岩土体水平位移的限制效果最为明显。因此,在该处设置不同长度的抗滑桩,分析不同桩长对于边坡变形的影响,其中桩长变化范围为10~50 m,得到的水平位移云图见图10。从图10可以看出:随着桩长的增大,边坡水平位移云图中的位移突变情况逐渐减少,位移变化趋势越来越均匀;最大位移也逐渐减小,分别为66.1, 57.2和51.6 mm。可见:当抗滑桩穿过结构面时,穿过的位置位于结构面下缘,相当于在结构面下部设置1个梢钉,将结构面钉在岩土体中;当桩长较小,如10 m时,边坡的最大位移为66.1 mm;随着桩长的增大,最大位移分别为57.2和51.6 mm,岩土体的变形得到进一步控制;但当桩长大于20 m时,位移的减小梯度并不大;增加桩长对坡体位移的控制效果不再明显。
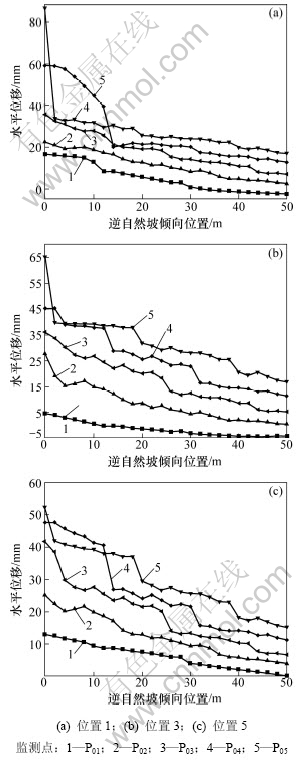
图8 不同抗滑桩位置下监测点水平位移
Fig.8 Horizontal displacement of monitoring points for different pile locations
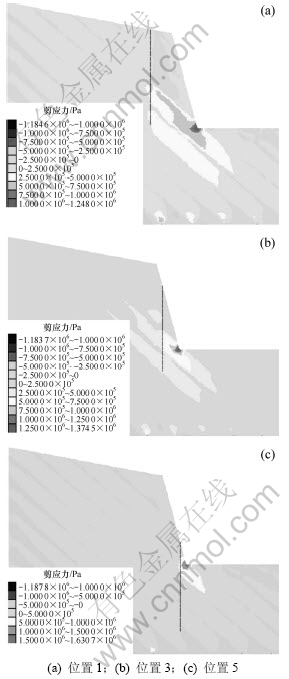
图9 不同抗滑桩位置下的剪应力云图
Fig.9 Shear stress contour of slope with different pile locations
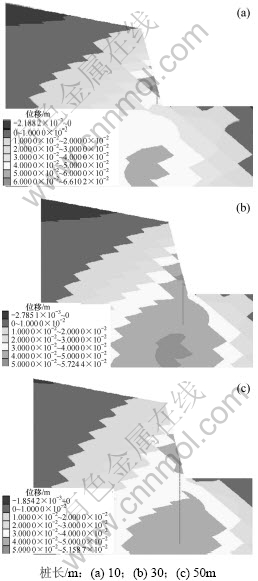
图10 不同抗滑桩桩长下的水平位移云图
Fig.10 Horizontal displacement contour of slope with different pile lengths
4 结论
(1) 抗滑桩位置对于边坡的水平位移影响较大,当抗滑桩位于坡面的中下部时(但需保证抗滑桩穿过了最危险滑动面),对于岩土体变形的效果最佳;抗滑桩的加固使岩体的水平位移变得更加均匀。抗滑桩位于坡脚时改变了此处岩土体的应力,明显减小了应力集中现象。
(2) 随着桩长的增大,边坡中的位移突变情况逐渐减少,位移变化趋势越来越均匀;最大位移也逐渐减小。存在一临界桩长Lcr,当桩长超过Lcr后,继续增大桩长对位移的控制效果不再明显。
参考文献:
[1] 陈祖煜. 土质边坡稳定性分析[M]. 北京: 中国水利水电出版社, 2003: 203-220.
CHEN Zu-yu. Analysis of soil slope stability[M]. Beijing: The Chinese Water Conservation and Electricity Press, 2003: 203-220.
[2] Ito T, Matsui T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 43-59.
[3] Ito T, Matsui T, Hong W P. Design method for stabilizing piles against landslide-one row of piles[J]. Soils and Foundations, 1981, 21(1): 21-37.
[4] Hassiotis S, Chameau J L, Gunatatne M. Design method for stabilization of slopes with piles[J]. Journal of Geotechnical and Geo-environmental Engineering, ASCE, 1997, 123(4): 314-323.
[5] 韦立德, 杨春和, 高长胜. 基于三维强度折减有限元的抗滑桩优化探讨[J]. 岩土工程学报, 2005, 27(11): 1350-1352.
WEI Li-de, YANG Chun-he, GAO Chang-sheng. Optimization of slide-resistant piles based on strength reduction method with 3D FEM[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1350-1352.
[6] 林杭, 曹平. 锚杆长度对边坡稳定性影响的数值分析[J]. 岩土工程学报, 2009, 31(3): 470-474.
LIN Hang, CAO Ping. Numerical analysis for the effect of cable length to the stability of slope[J]. Chinese Journal of Geotechnical Engineering, 2009, 31 (3): 470-474.
[7] 王启耀, 蒋臻蔚. 层状岩体的力学特征和数值模拟方法研究 [J]. 公路交通科技, 2005, 22(9): 111-115.
WANG Qi-yao, JIANG Zhen-wei. Study on the stress characteristic of layered rock and its numerical simulation methods[J]. Journal of Highway and Transportation Research and Development, 2005, 22(9): 111-115.
[8] 张传庆, 周辉, 冯夏庭, 等. 基于屈服接近度的围岩安全性随机分析[J]. 岩石力学与工程学报, 2007, 26(2): 292-299.
ZHANG Chuan-qing, ZHOU Hui, FENG Xia-ting, et al. Stochastic analysis method on safety of surrounding rock mass based on yielding approach index[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 292-299.
[9] 梁正召, 唐春安, 李厚祥, 等. 单轴压缩下横观各向同性岩石破裂过程的数值模拟[J]. 岩土力学, 2005, 26(1): 57-62.
LIANG Zheng-zhao, TANG Chun-an, LI Hou-xiang, et al. A numerical study on failure process of transversely isotropic rock subjected to uniaxial compression[J]. Rock and Soil Mechanics, 2005, 26(1): 57-62.
[10] Jeong S, Kim B, Won J, et al. Uncoupled analysis of stabilizing piles in weathered slopes[J]. Computers and Geotechnics, 2003, 30(8): 671-682.
[11] Grasselli G. 3D Behaviour of bolted rock joints: experimental and numerical study[J]. International Journal of Rock Mechanics & Mining Sciences, 2005(42): 13-24.
[12] Chow Y K. Analysis of piles used for slope stabilization[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1996, 20(9): 635-646.
(编辑 陈灿华)
收稿日期:2010-09-22;修回日期:2010-12-15
基金项目:国家自然科学基金资助项目(50099620)
通信作者:鲁光银(1976-),男,湖北宜昌人,博士,副教授,从事隧道地质灾害探测与评价工作;电话:13975894898;E-mail:luguangyin2006@126.com