DOI: 10.11817/j.issn.1672-7207.2016.03.020
层状地基中考虑桩侧水泥土与土的静钻根植桩单桩沉降计算
徐礼阁1, 2，王奎华1, 2，张鹏1, 2，吕述晖1, 2，李振亚1, 2
(1. 浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州，310058；
2. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州，310058)
摘要：基于荷载传递法和虚土桩模型，推导层状地基中考虑桩周、桩端土层分布和桩身-水泥土-土体相互耦合作用的静钻根植桩单桩沉降计算公式，并进一步讨论弹性极限位移、弹性抗剪切刚度系数、虚土桩长度等参数对单桩沉降的影响。最后利用静载试验实测数据，对比该计算方法的荷载-沉降曲线。研究结果表明：考虑土层分布及土和水泥土对桩体沉降影响的单桩沉降计算方法计算得到的桩顶沉降值与实测值较吻合，在实际工程应用中优于目前桩基设计规范的方法。
关键词：静钻根植桩；荷载传递法；层状地基；荷载-沉降曲线
中图分类号：TU473 文献标志码：A 文章编号：1672-7207(2016)03-0868-07
Calculation method for settlement of single static drill rooted pile considering cemented soil and soil around pile in layered soil
XU Lige1, 2, WANG Kuihua1, 2, ZHANG Peng1, 2, L
Shuhui1, 2, LI Zhenya1, 2
(1. MOE Key Laboratory of Soft Soils and Geoenvironmental Engineering, Zhejiang University,
Hangzhou 310058, China;
2. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China)
Abstract: Based on the load transfer method and virtual soil pile model, settlement calculation method of single static drill rooted pile was presented considering the soil distribution of pile side and pile end and the interaction among pile body, cemented soil and soil around pile. The effects of elastic limit displacement, elastic shear stiffness coefficient, length of virtual soil pile of single pile were analyzed. Finally, the calculation results of this method were compared with the measured settlement. The results show that within a certain range of load, the pile top settlement calculated by this presented method is approximate to the measured value, and also superior to the method in technical code for building pile foundations.
Key words: static drill rooted pile; load transfer method; layered soils; load-settlement curve
传统桩基受施工工艺的限制均存在一些不足，如预制桩的挤土效应、噪音、打桩破损，灌注桩的缩颈、桩底沉碴、钻孔泥浆污染环境等。静钻根植桩施工技术具有无振动、低噪声、成桩质量好、承载力高、泥浆排放少等优点。新桩型的应用对沉降计算、检测等配套技术也提出了新的要求。静钻根植桩下段一般采用预应力高性能混凝土扩径竹节桩(PHDC)，桩身带有等间隔等腰梯形突起[1]，桩身与桩周土作用更紧密，其下端扩大头可以提高桩端阻力。桩体上段一般采用复合配筋先张法预应力混凝土管桩[2](PRHC)，可以承受较大的水平荷载。中部根据设计桩长可以配置1~3根PHC管桩。静钻根植法施工竹节桩和复合配筋桩主要有以下4个步骤：1) 采用由液压控制扩大和收拢的钻头进行预钻孔；2) 采用专用钻头对孔底进行扩底；3) 在孔内注入规定配比的水泥浆；4) 边注浆边将预制桩植入钻孔内。在目前的设计中，常用规范法计算单桩沉降量[3-5]。但规范法不能考虑桩土间的相互作用和桩端土的分层、沉渣，因此，计算结果不理想。荷载传递法认为单桩竖向压力通过摩阻力和端阻力将荷载传递到地基土中。若能找到桩侧摩阻力和端摩阻力的分布函数，则可求得桩的沉降[6]。SEED等[7]提出，把桩体划分为若干单元，将土体对桩身的作用简化为弹簧。该法能较好地反映桩土之间的非线性相互作用和地基成层性。相应的弹簧模型有理想弹塑性模型、双折线(软化、硬化)模型、三折线软化模型等分段线性模型和双曲线模型、指数函数模型等非线性模型，每种模型都有其相适应的地质土体[8-10]。但因一些模型参数不易获得而较少应用。为了考虑桩端土对单桩沉降的影响，王奎华等[11-12]提出了虚土桩法。本文作者采用虚土桩模型计算静钻根植桩单桩沉降。
1 模型假设与公式推导
1.1 数学模型
桩端扩底成孔主要构造见图1，满足：1) Dz-Dj= 100~150 mm；2) Db≤1.5Dz；3) Lb≥3Dz。其中：Dz为未扩径段水泥土直径；Dj为竹节桩节状突起处直径；Db为扩径段水泥土直径；Lb为扩径段水泥土高度。
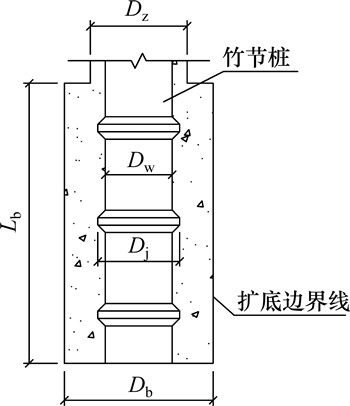
图1 桩端扩底示意图
Fig. 1 Diagram of hole enlargement at the tip of pile
传统荷载传递法将桩体单元周围土体对桩体的作用简化为弹簧的刚度，弹簧的刚度反映桩体相对土体位移与所受土体作用力之间的关系，由荷载传递函数定义。静钻根植桩因为其特殊的施工工艺，桩与桩侧土体之间填充着一层特殊介质水泥土。为了考察桩-水泥土-土体之间的耦合作用对桩身沉降的影响，提出了一种新的计算模型。在新的计算模型中，对第i段桩体单元隔离分析，认为土对桩身和水泥土的作用可以简化为刚度为ki1的弹簧，同样水泥土对于预制桩身的作用可以简化为刚度为ki2的弹簧，从而第i段桩体单元所受的桩侧作用力相当于2根刚度分别为ki1和ki2的弹簧的串联。
传统桩体单元划分时只需考虑土层性质的变化。对于静钻根植桩划分桩体单元，不仅需要考虑土体分层性质的变化，而且要考虑由于竹节桩桩径变化和桩底扩径，从而导致桩身截面和桩周水泥土厚度发生变化。依据桩身变化，将静钻根植桩分为2个不同桩段，即中上部PRHC和PHC组成的管桩段和下部的竹节桩段。管桩段内桩身和水泥土厚度不变，因此，只需依据土层性质变化来分层。因为竹节桩段桩身具有等间距的等腰梯形竹节状突起和桩底端的水泥土扩径，所以，在分层时不仅要考虑自然土层性质的变化而且在水泥土厚度变化处也要分层。鉴于竹节状突起一般为等腰梯形，目前，6种竹节桩标准图中，等腰梯形底边长度有2种，分别为225 mm和300 mm，为了保证计算精度，每个等腰梯形被划分为高度相等的3层单元，每个单元最大高度不超过100 mm，假设这样深度范围内土层性质不会发生改变。对于其中2个斜边单元，依据面积等效简化为矩形结构，即单个桩体单元内水泥土厚度不变。扩径和非扩径段采用相同的原则。对于虚土桩段，鉴于水泥土与桩身紧密的相互作用，虚土桩桩径一般取与竹节桩扩径桩段相等，不考虑虚土桩的扩散角，其单元划分仅需依据土层性质变化。
桩侧土和桩端土均采用理想弹塑性模型，水泥土在桩体达到极限承载力时一直处于弹性状态，见图2。
对于桩侧和桩端土体，其荷载传递函数为
(1)
式中：ui1b为第i段桩体单元桩侧土的弹性极限位移(mm)；fs为单位长度桩侧摩阻力(kN/m)；ki1为第i段桩单元桩侧受到土体的理想弹塑性模型的弹性抗剪切刚度系数(N/m2)。
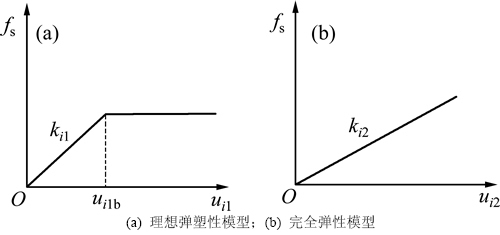
图2 土体与水泥土的本构模型
Fig. 2 Constitutive models of soil and cement-soil
由于对桩侧水泥土和土体的作用简化为刚度分别为ki2和ki1的2个弹簧串联，因此，第i段桩体单元桩侧弹簧刚度为
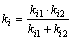(2)
1.2 基本假设
1) 桩体为均质变截面弹性杆件，不考虑桩身压缩的非线性。
2) 桩体中每个弹性单元的结点位移只与该结点处的侧摩阻力相关，桩侧极限摩阻力随深度线性增加。
3) 桩与桩侧土之间没有相对滑移，各桩段交界面接触连续，满足力与位移连续条件。
4) 对于桩侧土，当桩身截面位移小于ui1b时为弹性阶段，桩身截面位移大于ui1b时为塑性阶段，抗剪切刚度系数ki1沿深度不变。
5) 桩土破坏发生在土与水泥土交界面，水泥土应力应变符合线弹性关系。
6) 虚土桩沿深度方向不考虑扩散角，虚土桩端部为刚性支撑。
7) 在受力过程中，桩侧摩阻力极限值从上向下发挥，塑性区范围由上往下逐步发展。
8) 单桩承载力处于极限状态时，桩周土在水泥土接触面处出现塑性破坏，水泥土一直处于弹性状态。
1.3 解析解推导
当桩顶荷载较小时，桩截面位移小于ui1b，桩周土全部处于弹性状态，此时第i个桩段截面位移u(x)满足如下方程：
(3)
式中：Pi和si分别为第i段桩顶部荷载和沉降，Pi+1和si+1分别为桩底所受反力和沉降；zi为第i段桩体截面到桩顶的距离；Ei，Ai，ki分别表示第i段桩体的弹性模量、横截面积以及弹性抗剪切刚度系数；1≤i≤n，n为包含虚土桩在内的划分的桩体单元的总段数。第i段桩体单元的横截面积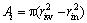
，对于组成静钻根植桩的PRHC，PHC和PHDC的空心桩，riw和rin分别为桩体单元的外半径和内半径；对于虚土桩实心桩体，定义rin=0。对于实体桩Ei为桩身弹性模量，对于虚土桩Ei为桩端土层的压缩模量。
定义如下表达式：
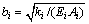(4)
求解式(3)可得第i桩段任意截面位移方程：
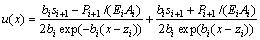(5)
联立式(3)和(5)可求得第i桩段桩顶荷载及位移：
(6)
由式(6)可得第i段桩单元桩顶部的刚度：
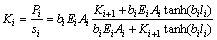(7)
式中：li为第i段桩体单元的厚度。
由假设条件6)可知，虚土桩桩端的位移边界条件为0，即
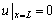(8)
式中：L为设计桩长与虚土桩长度之和。
由式(5)给出的第i段桩单元截面位移方程并结合边界条件(8)可以求得第n段桩单元顶部刚度：
(9)
根据式(7)和(9)可以递推得到桩身顶部刚度K1，进而在已知桩顶荷载P1的条件下，可以求得层状地基中静钻根植桩的桩顶沉降：
(10)
当桩侧土全部处于弹性阶段时，桩顶刚度为常数，即P-s曲线为直线段。
当桩顶荷载荷载较大时，桩截面位移大于ui1b，桩周土进入塑性变形阶段，根据理想弹塑性模型假定，此时处于塑性区的第i个桩段截面位移u(x)满足如下方程：
(11)
求解式(11)可得第i段桩单元截面位移方程：
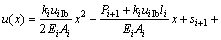
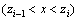(12)
则第i段塑性区桩体单元桩顶荷载Pi及位移si为
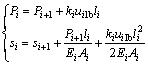(13)
由假设边界条件可知：虚土桩桩端位移为0，即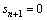
，则第n段桩体桩顶荷载Pn与位移sn的关系为
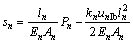(14)
通过上述公式推导可以获得完整的Q-s曲线，相关参数容易确定。
2 计算参数的确定
2.1 土体弹性极限位移
运用荷载传递法计算桩顶荷载，确定土体弹性极限位移ui1b是关键，从而可判断关乎桩侧土是否进入塑性变形和确定土体的抗剪切刚度系数。在未进行应变测试时，可以参考相关学者的建议值：对于预制桩，POPOUS[14]研究认为极限位移可取桩径的0.5%~ 1.0%；按照传统经验，桩侧摩阻力达到极限值只与土的类别有关而与桩径无关，根据实验资料，黏性土一般为2~6 mm，砂类土为6~10 mm[15]。
2.2 土体的抗剪切刚度系数
对于一般土体，弹性抗剪切刚度系数可以用下式计算：
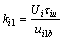(15)
在实际工程中，Ui为第i段桩体单元的桩身周长，极限侧摩阻力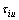
可以实测或者参考规范[3]的相关表格获得。但是需注意的是：由于静钻根植桩既不同于普通预制桩，也不同于钻孔灌注桩，静钻根植施工工艺搅拌水泥土使得桩身与桩侧土之间的摩擦力比预制桩和灌注桩的极限侧阻力标准值
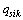都要大，因此，规范推荐值尽量取大。本文在计算时所取值为相应预制桩推荐值的最大值。通过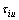和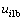
就可以得到土体的弹性抗剪切刚度系数
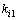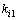，即为土体理想弹塑性模型折线的割线刚度。
2.3 水泥土的弹性抗剪切刚度系数确定
根据剪切位移理论，对均质地基中各向同性、弹性土介质中的弹性抗剪切刚度系数可以采用下式 计算：
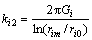(16)
式中：ri0为桩半径；rim为影响半径；Gi为弹性质剪切模量，
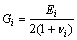(17)
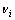为相应桩体单元周围的水泥土的泊松比。
假定桩侧搅拌均匀的水泥土是均质、各向同性的弹性的特殊土介质，则可以采用式(16)计算某桩体单元周围的水泥土的弹性抗剪切刚度系数ki2。
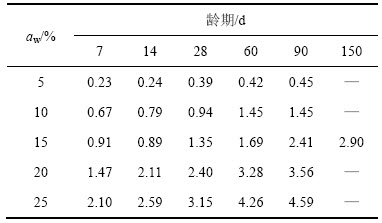
根据文献[16]，不同水泥掺合比(aw)的水泥土无侧限抗压强度与龄期的关系如表1所示。水泥土强度随龄期的增长而增大，规范建议以90 d龄期的无侧限抗压强度作为水泥土的强度标准值[17]。
表1 不同掺合比和不同龄期下水泥土无侧限抗压强度
Table 1 Unconfined compressive strength of cement-soil under different blend ratio and ages MPa
对于水泥土的压缩特性，马军庆等[18]通过对大量水泥土样本的统计分析，认为变形模量E与无侧限抗压强度qu的关系可表示为E=(120~150)qu，一般取E=142qu比较合适。
静钻根植桩扩底完成后，桩端和桩周按照钻孔体积注入设计体积比的水泥浆，换算成质量掺合比约为20%。从而由表1可知其无侧限抗压强度，并通过式(16)和(17)换算可以得到各桩体单元周围水泥土的弹性抗剪切刚度系数ki2。
2.4 桩端土长度取值
虚土桩桩端一般位于基岩或者桩端应力已消散区域，基本没有沉降，因此，虚土桩桩端位移取为0 m。影响虚土桩段长度的因素主要为实体桩端土性质和桩端应力。王奎华等[19]认为虚土桩长度一般可以取5~10 m。
3 工程实例对比
本实例来自浙江温州电厂扩建工程汽轮机房区域的2根静钻根植桩，桩号分别为ZW57和ZW83。桩ZW-57的桩顶标高-4.6 m(都以1985年国家高程为基准)，设计桩长54 m，从下到上配装方式依次为：PHDC800-600(130)AB-15+PHC800(130)A-12+PHC800 (130)AB-12+PRHC800(130)I-15，共4节；桩ZW-83的桩顶标高-1.6 m，设计桩长57 m，从下到上配装方式依次为：PHDC800-600(130)AB-15+PHC800(130)A- 12+PHC800(130)AB-12+PRHC800(130)Ⅰ-9, 9，共5节。桩身混凝土等级都为C80，混凝土弹性模量Ec= 38 GPa。采用静钻根植桩施工工艺沉桩，钻孔直径为900 mm，桩底扩径直径为钻孔直径的1.5倍，即1 350 mm，扩径深度取3 m。ZW57和ZW83桩侧土及桩端土的物理力学性质分别见表2和表3。
ZW-57虚土桩从桩底取到12层黏土8-2底部，虚土桩长为11.95 m；ZW83虚土桩从桩底取到14层黏土8-2底部，虚土桩长度为12.5 m，鉴于桩长较长且桩端直径较大，虚土桩段不考虑扩散角。桩端土黏土8-2、粉质黏土8-3的弹性模量分别为7 MPa和10.5 MPa，桩身弹性模量为38 GPa。桩周水泥土质量掺合比约为20%，90 d时的无侧限抗压强度为3.56 MPa(表1)。桩ZW-57共划分为桩体单元74段，桩ZW-83共划分为桩体单元76段。依据本文方法编程计算和静载实测数据对比见图3和图4。其中，ZW-57加载到桩身沉降出现塑性变形，ZW-83荷载试验桩身沉降未出现突降变形。
表2 ZW57号桩基地质参数
Table 2 Geological parameters of pile ZW57
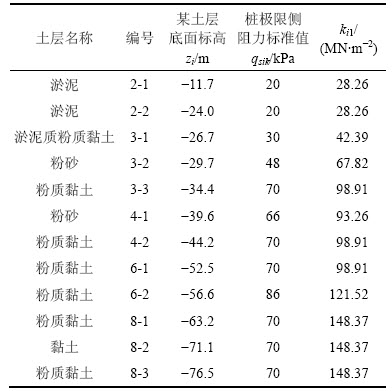
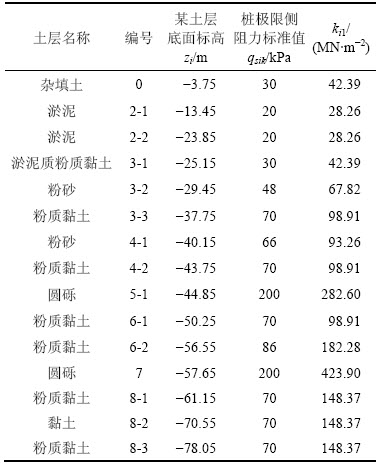
表3 ZW83号桩基地质参数
Table 3 Geological parameters of pile ZW83
从2根桩的静载实测结果与理论计算结果对比可以发现，本文提出的计算方法与实际情况比较符合。当桩顶荷载较小时，桩侧土处于完全弹性状态，Q-s曲线近似为直线，理论计算值与实测值基本重合；当桩顶荷载逐渐加大时，桩周土出现塑性变形，此时理论值比实测值偏大。从图3可以看出：ZW-57桩的竖向抗压极限承载力小于6.6 MN，可取为6.1 MN。由理论计算曲线分析确定的单桩极限承载力为6.2 MN左右。这可能有2个因素造成：1) 桩周水泥土的质量掺合比约为20%，在理论计算时，依据规范要求，采用水泥土90 d龄期的强度，但是实际静载试验时约在成桩1月后进行，所以，水泥土强度及桩周土固结沉降可能都在发展过程中；2) 理论计算时，将桩体当作完全单桩条件分析，但计算桩体在实际布置时与周围桩体组成群桩，其桩间距为桩径的2~3倍，在周围桩体施工时可能造成对测试桩桩周土的不利扰动。由于现在建筑桩体设计一般都以沉降变形为控制条件，桩体很少达到极限承载力，在达到极限承载力之前，本方法理论计算沉降和实测沉降曲线较接近且略大，偏安全，且相关参数易获得，因此，该法可以用于设计计算。
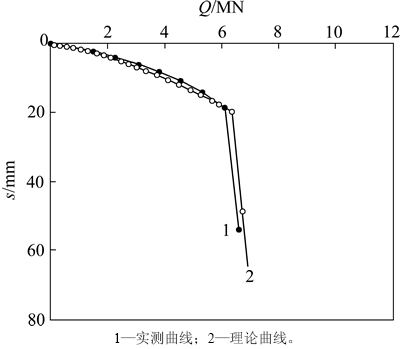
图3 ZW-57桩顶沉降实测结果与计算值
Fig. 3 Measured settlement results and calculated settlement of pile ZW-57’s top
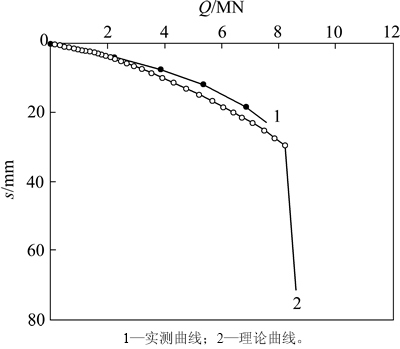
图4 ZW-83桩顶沉降实测结果与计算值
Fig. 4 Measured settlement result and calculated settlement value of pile ZW-83’s top
4 结论
1) 本文考虑预制桩-水泥土-土体三者耦合作用及桩段土体分层特性的荷载传递计算方法与荷载试验结果有着较好的一致性。本文计算方法简单，参数明确，可用于现场单桩沉降量的计算评测，为设计提供较准确的沉降值。
2) 桩侧水泥土和土体的弹性抗剪切刚度系数的取值是影响计算效果的关键。各种土体的弹性极限位移有待进一步研究。目前对水泥土的相关研究主要集中于水泥浆和黏性土体的混合，水泥浆与其他土体的研究也有待进一步进行。
参考文献：
[1] 2012浙G37, 静钻根植先张法预应力混凝土竹节桩[S].
2012 Zhe G37, Prestressed concrete bamboo-like pile constructed by static drill ground method[S].
[2] 2012浙G36, 复合配筋先张法预应力混凝土管桩[S].
2012 Zhe G36, Prestressed concrete pipe pile of composite reinforcement[S].
[3] JGJ 94—2008, 建筑桩基技术规范[S].
JGJ 94—2008, Technical code for building pile foundations[S]
[4] COYLE H M, REESE L C. Load transfer for axially loaded piles in clay[J]. Journal of Soil Mechanics& Foundations, 1966, 92(2): 1-26.
[5] RANDOLPH M F, WORTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of Soil Mechanics and Foundations Division, ASCE, 1978, 12: 56-61.
[6] 陈祥福. 沉降计算理论及工程实例[M]. 北京: 科学出版社, 2005: 207-208.
CHEN Xiangfu. Settlement calculation theory and engineering examples[M]. Beijing: Science Press, 2005: 207-208.
[7] SEED H B, REESE L C. The action of soft clay along friction piles[J]. Transactions, ASCE, 1957, 122: 731-754.
[8] 罗永健. 考虑虚土桩扩散角时基桩沉降计算理论及工程引用[D]. 杭州: 浙江大学建筑工程学院, 2013: 7-12.
LUO Yongjian. Settlement calculation theory of single pile considering cone angle of fictitious pile and its application[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2013: 7-12.
[9] 彭吉五. 考虑基岩埋置深度影响时单桩沉降特性研究[D]. 杭州: 浙江大学建筑工程学院, 2007: 3-7.
PENG Jiwu. Research on the settlement of single pile considering the effect of embedded depth for bedrock[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2007: 3-7.
[10] 杨冬英．复杂非均质土中桩土竖向振动理论研究[D]. 杭州: 浙江大学建筑工程学院, 2009: 2-8.
YANG Dongying. Study on pile vertical vibration in inhomogeneous soil[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2009: 2-8.
[11] 王奎华, 刘凯, 吴文兵, 等. 虚土桩扩散角对桩的纵向振动特性影响研究[J]. 工程力学, 2011, 28(9): 129-136.
WANG Kuihua, LIU Kai, WU Wengbing, et al. Effect of cone angle on axial dynamic response of fictitious soil pile[J]. Engineering Mechanics, 2011, 28(9): 129-136.
[12] 王奎华, 吴文兵, 马少俊, 等. 桩底沉渣对桩的纵向振动特性影响研究及应用[J]. 岩土工程学报, 2011, 33(8): 1227-1234.
WANG Kuihua, WU Wengbing, MA Shaojun, et al. Influence of sediment on vertical dynamic response of pile embedded in inhomogeneous soil and its application[J]. Geotechnical Engineering, 2011, 33(8): 1227-1234.
[13] 陈龙珠, 梁国钱, 朱金颖, 等. 桩轴向荷载沉降曲线的一种解析算法[J]. 岩土工程学报, 1994, 16(6): 30-38.
CHEN Longzhu, LIANG Guoqian, ZHU Jinying, et al. Analytical calculation of axial loading-settlement carve of piles[J]. Geotechnical Engineering, 1994, 16(6): 30-38.
[14] POPOUS H G. Twenty-ninth Rankine lecture: pile behavior- theory and application[J]. Geotechnique, 1989, 39(3): 363-415.
[15] 莫海鸿, 杨小平. 基础工程[M]. 2版. 北京: 中国建筑工业出版社, 2008: 129-130.
MO Haihong, YANG Xiaoping. Foundation engineering[M]. 2nd ed. Beijing: China Architecture & Building Press, 2008: 129-130.
[16] 龚晓南. 复合地基理论及工程应用[M]. 2版. 北京: 中国建筑工业出版社, 2007: 25-29.
GONG Xiaonan. Composite foundation theory and engineering application[M]. 2nd ed. Beijing: China Architecture & Building Press, 2007: 25-29.
[17] JGJ 79—2012, 建筑地基处理技术规范[S].
JGJ 79—2012, Technical code for building foundation treatment[S].
[18] 马军庆, 王有熙, 李红梅, 等. 水泥土参数的估算[J]. 建筑科学, 2009, 25(3): 65-67.
MA Junqing, WANG Youxi, LI Hongmei, et al. Studying on the relations of cement-soil parameters with compressive strength[J]. Building Science, 2009, 25(3): 65-67.
[19] 王奎华, 罗永健, 吴文兵, 等. 层状地基中考虑桩端应力扩散的单桩沉降计算[J]. 浙江大学学报(工学版), 2013, 47(3): 472-479.
WANG Kuihua, LUO Yongjian, WU Wenbing, et al. Calculation method for settlement of single pile considering stress dispersion of pile end soil[J]. Journal of Zhejiang University (Engineering Science), 2013, 47(3): 472-479.
(编辑 赵俊)
收稿日期：2015-03-08；修回日期：2015-04-28
基金项目(Foundation item)：国家自然科学基金资助项目(51378464) (Project(51378464) supported by the National Natural Science Foundation of China)
通信作者：王奎华，博士，教授，从事岩土工程基础理论的研究；E-mail: zdwkh0618@Zju.edu.cn
