铁路客运专线模糊k近邻客流预测模型
豆飞1, 2,贾利民3,秦勇1, 3,徐杰1, 3,王莉1, 3
(1. 北京交通大学 交通运输学院,北京,100044;
2. 北京市地铁运营有限公司 地铁运营技术研发中心, 北京,102208;
3. 北京交通大学 轨道交通控制与安全国家重点实验室,北京,100044)
摘要:客运专线客运量在短时期内体现准周期的规律性变化,且受多种因素的影响呈现出一种复杂的非线性特点。传统的预测方法不能完全反映客流量准周期性和非线性的特点,预测结果误差相对较大。为更准确地预测铁路客运专线客运量,通过分析客运专线的客流特征,总结相邻时段客流变化规律,在确定相邻时段之间客流变化率的基础上,将客流变化情况划分为8个不同的等级,依据客流变化情况划分的不同等级对客流变化率模糊化,并利用客流变化率模糊值的时序关系,建立客运专线模糊k近邻客流预测模型。通过实例分析,与其他预测方法进行比较,证明该模糊k近邻客流预测结果误差更小,精度更高,为预测铁路客运专线客运量提出一种新思路。
关键词:客运专线;客运量;客流预测;模糊;k近邻法
中图分类号:U293.13 文献标志码:A 文章编号:1672-7207(2014)12-4422-09
Fuzzy k-nearest neighbor passenger flow forecasting model of passenger dedicated line
DOU Fei1, 2, JIA Limin3, QIN Yong1, 3, XU Jie1, 3, WANG Li1, 3
(1. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China;
2. Subway Operation Technology Centre, Mass Transit Railway Operation Corporation LTD, Beijing 102208, China
3. State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044, China)
Abstract: Passenger flow of passenger dedicated line shows the quasi-periodic variations in the short-term forecasts, and also shows complex nonlinear characteristics because of many factors. The traditional prediction model can’t fully reflect quasi-periodic and nonlinear characteristics of the passenger flow, which result in larger errors in forecast results. In order to forecast the passenger flow more accurately, the passenger flow characteristics of the high-speed railway were analyzed, and variation of passenger flow in the adjacent period was summed up. Passenger flow change rate was divided into different grades and fuzzified on the basis of passenger flow change rate between adjacent periods. Also, fuzzy k-nearest neighbor prediction model was established on the basis of the fuzzy values timing relationship of passenger flow change rate. By comparing it with other predictive methods, the prediction result of fuzzy k-nearest neighbor prediction model is proved to be more accurate and precise, thus providing a new idea for the railway passenger flow forecast.
Key words: passenger dedicated line; traffic volume; passenger flow forecasting; fuzzy; k-nearest neighbor
随着我国高速铁路网的不断完善,路网内地区之间的连通性增强,跨地区的客流流动逐渐加大。客运专线的客流量是制定运营模式和行车组织方案的重要依据,客流预测直接影响客运组织方案与客运计划的确定。其中,短期客流预测结果直接影响近期客流计划编制,有助于客运部门针对客流短期波动情况作出快速响应,去制定最优的列车开行方案,有效组织旅客运输力量,最大化经济效益和社会效益。一般而言,客流预测可分为相关因素预测法和时间序列预测法。相关因素预测法是找出影响客流量的因素,建立客流量和各种影响因素之间的函数关系,得出模型进行预测。有些预测工作者考虑运输竞争、OD分区、社会经济发展水平、技术条件、国民收入等因素的影响,建立了很多相关因素预测模型进行客流预测,包括神经网络模型、Logit模型和MD模型等。王卓等[1-4]在改进神经网络模型的基础上,建立了客运量神经网络预测模型,对铁路客运量进行了预测。郑辉[5]根据城际铁路运输及客流预测的特点,采用Logit模型,并经过参数拟合和调整,预测了城际铁路客流情况。李倩[6]从时间的动态性和空间的网络性阐述了高速铁路网客流的变化趋势,分析了高速铁路网的客流特点,以四阶段法为基础,提出了基于路网的高速铁路客流预测方法。夏烈[7]在MD模型中提出了广义出行时间和广义出行费用的概念,在出行牺牲量计算中考虑了出行耗时、出行费用、旅行舒适度等众多因素,分析了趋势运量、诱增运量、转移运量在MD模型中的关系,最终确立了MD模型客流预测流程,并证明了改进MD模型对客运专线客流预测的可靠性和合理性。
时间序列预测法是以时间为自变量建立客流预测模型。既有的时间序列预测法包括基于时间序列分析的客流预测方法、季节模型、灰色模型等预测方法。Tian等[8]在分析了客流时间分布规律的基础上,建立了时间序列客流预测模型。王超等[9]提出了一种基于时间序列的趋势外推模型,并分析了节假日客流数据变化规律,通过预测对模型进行了完善。王芳[10]分析了季节调整模型原理,并介绍了季节调整模型在客运量短期预测中的应用。孙晚华等[11]分析了影响城际客流的因素,利用灰色理论中系统关联度分析方法,构建了一种新的铁路城际客流灰色预测模型。李海军等[12]提出了基于灰色模型及月度比例系数法的铁路客流预测方法,并证明了该方法计算简便及可操作性强。由于客运专线客流量的多种影响因素之间错综复杂关系,带来了自变量选取上的困扰,且预测过程中相关因素本身的未来值也不确定,预测结果误差较大。从统计资料来看,自2005年以来无论是全国还是某一地区的客运量都随时间推移而稳步上升,时间变量是一个综合的自变量,与客运量高度相关。本文作者考虑到历史客流数据存在一定的规律性,历史客流状况容易重现,通过分析客运专线的客流特征,总结相邻时段间客流变化规律,依据铁路客运专线客流变化程度的认知习惯,将客流变化情况划分8个不同等级,对客流变化率模糊化,建立模糊k近邻客流预测模型,实例分析证明该模型合理有效,并将预测输出值与其他预测模型输出值进行对比,验证了该模型预测结果误差更小。
1 客流特征分析
已有的客流预测方法往往由于对高速铁路网的客流特征分析不够,导致所构建的客流预测模型不合理,客流预测结果不准确。因此,分析高速铁路的客流特征是准确预测高速铁路客流的基础。本文在预测短期客流量时,主要考虑时间变量与客流量的高度相关性,分析与时间变量相关的高速铁路的客流特征,以高速铁路北京南—廊坊客流为研究对象,选取2011-09-29—2011-10-08每天8:00—18:00的客流数据,时间间隔为0.5 h,如图1所示。

图1 北京—廊坊高速铁路客流量变化规律
Fig. 1 Passenger flow variation of high-speed railway between Beijing and Langfang
通过客流变化情况的分析,客流特征主要表现在以下2个方面:
1) 短期客流的非线性波动。高速铁路具有快速、方便、舒适、安全、准时等特征,其客流来源广泛。中、长途距离出行的乘客对出行时效要求较高,会倾向于选择高速铁路出行,另外,客流量随着高速铁路开通时间的推移而增加。由于高速铁路客流量受多种因素的影响,所以短时间内客流变化率不稳定,客流量呈现非线性波动,此特征在图1中体现明显。
2) 客流准周期波动显著。高速列车因运行速度快,间接缩短了城市间距离,其每天运行时间一般为6:00—24:00。因而,在铁路客流构成中,探亲、商务、旅游、公务出差所占比例较大,客运专线客流以7 d为循环周期波动,通常周一至周四客流量比较平稳,周五客流量开始增长,周六、日客流量达到高峰[13]。在日客流量中,早晚高峰客流量较大,平峰期客流较为平缓,客流的准周期波动明显,如图1所示。
2 客流变化的规律性
相关符号定义如下:
p(t)为历史客流数据中第t时段的客流量;
n为历史客流量所包含的时段个数;
v(t) 为第t时段的客流量p(t)到下一个时段的客流量p(t+1)的客流变化率;
ui为客流变化率区间,i=1,2,…,8;
ui′为客流变化率区间ui的中间值,i=1,2,…,8;
Ai为模糊语义变量。
客运专线某两地间的客流量以一定的时段进行统计,考虑不同时段的历史客流量分别为p(1),p(2),…,p(t-1),p(t),p(t+1),…,p(n-1),p(n)。同时考虑相邻时段之间的客流变化情况,分别记作v(1),v(2),…,v(t-1),v(t),v(t+1),…,v(n-2),v(n-1)。进而分析客流变化率,总结相邻时段间客流变化的规律。
2.1 客流变化率
为了能更清楚、更准确地综合表达相邻时段的客流变化趋势,将客流变化率进行标准化处理。
定义标准化的客流变化率为 ,其中,
,其中,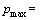
 ,表示已知客流变化量的最大值。当
,表示已知客流变化量的最大值。当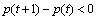 时,则称第t时段的客流量到第t+1时段的客流量递减;当
时,则称第t时段的客流量到第t+1时段的客流量递减;当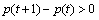 时,则称第t时段的客流量到第t+1时段的客流量递增;当p(t+1)-p(t)=0时,则称第t时段的客流量到第t+1时段的客流量无变化。
时,则称第t时段的客流量到第t+1时段的客流量递增;当p(t+1)-p(t)=0时,则称第t时段的客流量到第t+1时段的客流量无变化。
例如,选取2011-10-10T8:00—2011-10-11T9:00北京—廊坊高速铁路的客流数据,客流数据以0.5 h为1个时段采集,结果如表1所示。其中,相邻时段客流变化量最大值

 ,计算得到相邻时段2011-10-10T8:00—8:30至8:30—9:00的客流变化率为
,计算得到相邻时段2011-10-10T8:00—8:30至8:30—9:00的客流变化率为
 ,依次可计算其他相邻时段客流变化率。
,依次可计算其他相邻时段客流变化率。
表1 客流数据
Table 1 Passenger flow data

2.2 客流变化规律
为清楚地体现客流变化趋势的规律性,依据铁路客运专线客流变化程度的认知习惯,并应用Zadeh的模糊集理论[14-16]将客流变化率划分为8个区间,分别表示不同程度的客流变化情况。
设论域U={u1,u2,u3,u4,u5,u6,u7,u8},其中,u1=[-1,-0.75],u2=[-0.75,-0.5],u3=[-0.5,-0.25],u4=[-0.25,0],u5=[0,0.25],u6=[0.25,0.5],u7=[0.5,0.75],u8=[0.75,1]。不同客流变化率区间的中间值为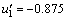 ,
,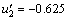 ,
, ,
,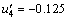 ,
,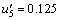 ,
, ,
, ,
, 。
。
定义A为模糊集,令A={A1,A2,A3,A4,A5,A6,A7,A8},其中,A1表示客流量下降幅度过大,A2表示客流量下降幅度较大,A3表示客流量下降幅度微大,A4表示客流量下降幅度较小,A5表示客流量上升幅度较小,A6表示客流量上升幅度微大,A7表示客流量上升幅度较大,A8表示客流量上升幅度过大。
因为客流变化率属于实数域R的范围内,可以根据时段间的客流变化情况来确定分布中所含的参数,这里采用指派法来确定模糊子集Ai的隶属度函数,分别为:
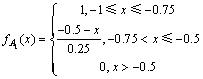
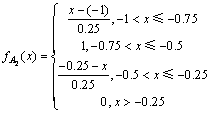
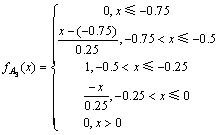

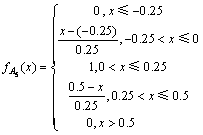
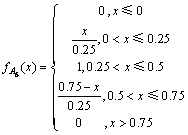
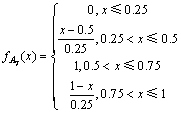
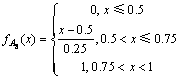
不同的客流变化率属于不同的模糊集,例如,表1中,时段8:00—8:30至时段8:30—9:00的客流变化率为0.132,属于模糊集A5;时段8:30—9:00至时段9:00—9:30的客流变化率为-0.103,属于模糊集A4;时段9:00—9:30至时段9:30—10:00的客流变化率为0.42,属于模糊集A6。客流变化率的模糊过程如图2所示。
基于模糊化的客流变化率,确立各相邻时段客流变化率模糊值的时序关系:
 ,
,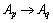 ,…,
,…,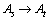
这里,“ ”表示“第t-1时段到第t时段的客流变化率为Aj,则第t时段到第t+1时段的客流变化率为Ap”。以表1中的客流数据为例,时间段在8:00—8:30的模糊客流变化率为A5,时间段在8:30—9:00 的模糊客流变化率为A4。那么可以确定它们之间的模糊值时序关系为A5→A4。表1中其他模糊值时序关系同样可以得到,如A5→A4,A4→A6,A6→A2,A2→A5等,结果如图3所示。因此,可以得到相邻时段客流变化率模糊值的时序关系,如表2所示。从表2可知:前一时段客流变化率模糊值为A5,其后时段客流变化率模糊值只有为A4,A5,所以对应的模糊值时序关系分别为A5→A4和A5→A5。
”表示“第t-1时段到第t时段的客流变化率为Aj,则第t时段到第t+1时段的客流变化率为Ap”。以表1中的客流数据为例,时间段在8:00—8:30的模糊客流变化率为A5,时间段在8:30—9:00 的模糊客流变化率为A4。那么可以确定它们之间的模糊值时序关系为A5→A4。表1中其他模糊值时序关系同样可以得到,如A5→A4,A4→A6,A6→A2,A2→A5等,结果如图3所示。因此,可以得到相邻时段客流变化率模糊值的时序关系,如表2所示。从表2可知:前一时段客流变化率模糊值为A5,其后时段客流变化率模糊值只有为A4,A5,所以对应的模糊值时序关系分别为A5→A4和A5→A5。
通过对客流特征的分析,高速铁路短期客流具有非线性、准周期性的特点,总结历史客流变化规律,利用各相邻时段间客流变化趋势(客流变化率模糊值时序关系)的相似特点,计算当前时段客流变化率v(n),由客流变化率公式计算预测时段客流量为p(n+1)=p(n)+pmax·v(n),具体计算过程在下节的客流预测模型中介绍。
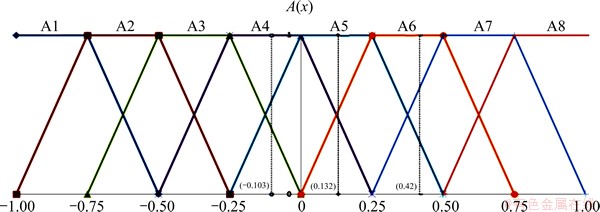
图2 客流变化率模糊化
Fig. 2 Fuzzified passenger flow change rate
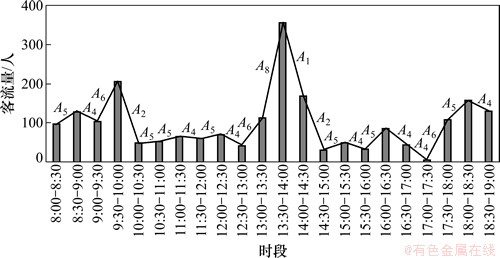
图3 客流变化时序关系图
Fig. 3 Passenger flow change rate relationships
表2 客流变化率模糊值的时序关系
Table 2 Fuzzy logic relationship of fuzzified passenger flow change rate

3 模糊k近邻客流预测模型
相关符号定义如下:
ki为客流变化率属于客流变化率区间ui的个数;
k为近邻数;
d为当前数据状态变化率向量的维数;
P(t)为第t时段的客流状态向量;
V(t)为与客流状态向量P(t)相对应的历史客流变化率向量。
定义历史客流状态向量即第t时段的客流状态向量为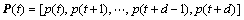 ,时段间的历史客流变化率向量为
,时段间的历史客流变化率向量为 。当t=n-d时,P(n-d)是当前客流状态向量,V(n-d)是当前客流变化率向量。为了更清晰地比较各时段客流量间的关系,分别给出客流状态矩阵及客流变化率矩阵,客流状态矩阵为
。当t=n-d时,P(n-d)是当前客流状态向量,V(n-d)是当前客流变化率向量。为了更清晰地比较各时段客流量间的关系,分别给出客流状态矩阵及客流变化率矩阵,客流状态矩阵为
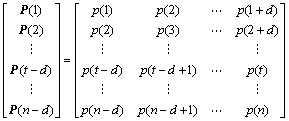
客流变化率矩阵为
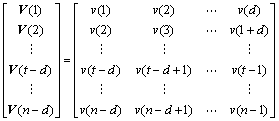
在模糊k近邻客流预测模型中,首先计算当前客流状态向量与历史客流状态向量之间的度量距离即欧式距离,公式表示为
 (1)
(1)
按照其距离从小到大排列历史客流状态向量,选择最近历史客流状态向量,然后比较其历史客流数据间与当前客流数据间的模糊逻辑关系,选择模糊逻辑关系相同的客流状态向量,并计算其变化率间的度量距离即欧式距离,公式表示为
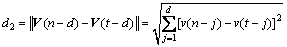 (2)
(2)
按照距离从小到大排列选择出k个最近历史客流状态向量
 的输出客流量
的输出客流量 ,其中,h=1,2,…,k,
,其中,h=1,2,…,k, 为
为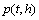 的下一个时段的客流量,计算这k个客流变化率
的下一个时段的客流量,计算这k个客流变化率
 ,用这些k个客流变化率来预测得到未知的客流变化率,进而计算得到第n+1时段的客流量。
,用这些k个客流变化率来预测得到未知的客流变化率,进而计算得到第n+1时段的客流量。
建立针对客运专线客流特点的模糊k近邻客流预测模型即FKNN (fuzzy k-nearest neighbor passenger flow forecast model),该模型的流程图如图4所示。
该模型的具体步骤如下。
步骤1:取近邻数初始值k=1;
步骤2:取当前客流状态变化率向量维数的初始值d=1;
步骤3:从预测第l=n+1时段的客流量开始;
步骤4:利用距离式(1),计算当前客流状态向量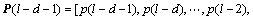
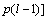 与历史客流状态向量
与历史客流状态向量
 之间的距离,根据距离从小到大进行对应的历史客流状态向量排序,得到排列后的历史客流状态向量为
之间的距离,根据距离从小到大进行对应的历史客流状态向量排序,得到排列后的历史客流状态向量为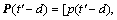
 ,并求得所对应的历史客流变化率向量为
,并求得所对应的历史客流变化率向量为
 ;
;

图4 模糊k近邻客流预测模型流程图
Fig. 4 Procedure of fuzzy k-nearest neighbor passenger flow forecast model
步骤5:将当前客流变化率向量 所对应的变化趋势
所对应的变化趋势 和排列后的历史客流变化率向量
和排列后的历史客流变化率向量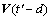 所对应的变化趋势
所对应的变化趋势 进行比较,选择变化率模糊值时序关系相同的前2k个历史客流状态向量;
进行比较,选择变化率模糊值时序关系相同的前2k个历史客流状态向量;
步骤6:利用距离式(2),计算前2k个历史客流状态向量所对应的历史客流变化率向量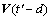 与当前客流变化率向量
与当前客流变化率向量 的欧式距离,且根据距离从小到大进行对应的向量排序,搜索出客流量及其变化率最接近的前k个历史客流向量为所求k个最近邻客流状态向量,即
的欧式距离,且根据距离从小到大进行对应的向量排序,搜索出客流量及其变化率最接近的前k个历史客流向量为所求k个最近邻客流状态向量,即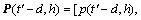
 ,得到
,得到 的输出客流量
的输出客流量 及
及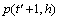 ,其中,h=1,2,…,k;
,其中,h=1,2,…,k;
步骤7:计算客流变化率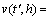
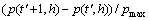 ,其中,h=1,2,…,k,将这k个客流变化率分别归入不同客流变化率模糊集,所属模糊集Ai的个数为ki,进行加权平均计算得到第l-1时段的客流变化率为
,其中,h=1,2,…,k,将这k个客流变化率分别归入不同客流变化率模糊集,所属模糊集Ai的个数为ki,进行加权平均计算得到第l-1时段的客流变化率为

步骤8:计算预测值 ,这里,
,这里,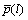 为客流量p(l)的预测值。将第l时段的客流预测值添加到历史客流数据中,令l=l+1,转步骤4,直到预测出最后时段l=M转步骤9,M为要预测的最后一个时段;
为客流量p(l)的预测值。将第l时段的客流预测值添加到历史客流数据中,令l=l+1,转步骤4,直到预测出最后时段l=M转步骤9,M为要预测的最后一个时段;
步骤9:计算预测值和实际值之间的均方根误差δRMSE即:
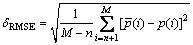
步骤10:令d=d+1,转步骤3,直到d=dmax转步骤11;
步骤11:令k=k+1,转步骤2,直到k=kmax转步骤12;
步骤12:选择最小均方差的一组预测客流量为最终客流预测值。
4 实例分析
实际数据是从2011-10-10到2012-01-07京津城际客运专线北京至廊坊8:00—18:00的客流数据,以0.5 h为1个时段,共1 800个客流数据。根据选取的客流数据特点,取当前客流状态量最大维数dmax=10,最大近邻数kmax=20,前83 d共1 660个客流数据作为已知的历史客流数据,后7 d共140个客流数据作为测试数据。采用MATLAB7.1进行编程预测,当近邻数k=13,客流变化率向量维数d=4时,预测结果均方根误差δRMSE最小,即δRMSE=1.998,FKNN客流预测输出值与实际值对比如图5所示。同时,对比ARIMA预测模型、KNN预测模型、FKNN预测模型的输出值,如图6所示,并且对比平均绝对误差、平均绝对误差以及均方根误差,如表3所示,分析结果表明:FKNN客流预测模型的预测误差最小,预测值更为精确。
根据历史客流数据的特征来确定当前客流状态向量的最大维数dmax。通过多次实验发现,若维数过大,则当前客流状态向量包含数据量冗余,导致计算时间过长,误差较大;若维数太小,则当前客流状态向量所包含的客流数据量无法准确体现出客流变化情况,同样导致误差较大。
表3 FKNN预测方法与其他预测方法的预测结果比较
Table 3 Comparison between ARIMA, KNN, and FKNN models


图5 FKNN预测值与实际值对比
Fig. 5 Comparisons of predictive values and real values

图6 FKNN,KNN,ARIMA预测值与实际值对比
Fig. 6 Comparisons of predictive values of three models with real values
在选取最大近邻数kmax值时,若k取值太大,则会将匹配强度较低的数据作为观测数据,从而引起误差增大;若k取值太小,则可能会引入个别波动强烈的客流数据与当前客流数据进行匹配,同样引起较大误差。
5 结论
1) 通过分析与时间变量相关的高速铁路客流特征,以时段作为综合变量考虑,建立了模糊k近邻客流预测模型,预测结果验证了该模型的合理性,并分析了平均绝对误差、平均绝对百分比误差及均方根误差,检验了该方法比其他预测模型的预测结果更为精确。
2) 该方法根据客流的变化趋势预测客流量,必须建立在大量客流数据的基础上进行客流预测,所以对于基础数据的收集、处理及修正,需要进一步加强。此外,对于当前客流状态向量的最大维数和最大近邻数的确定需要经过多次试验及更多的数据分析,仍需要进一步研究。
参考文献:
[1] 王卓, 王艳辉, 贾利民, 等. 改进的BP神经网络在铁路客运量时间序列预测中的应用[J]. 中国铁道科学, 2005, 26(2): 128-131.
WANG Zhuo, WANG Yanhui, JIA Limin, et al. The application of improved BP neural network in the prediction of railway passenger volume time serial[J]. China Railway Science, 2005, 26(2): 128-131.
[2] WEI Yu, CHEN Muchen. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks[J]. Transportation Research Part C, 2012, 21(1): 148-162.
[3] WANG Yao, ZHENG Dan, LUO Shimin, et al. The research of railway passenger flow prediction model based on bp neural network[J]. Advanced Materials Research, 2013, 605: 2366-2369.
[4] ZHAO Shuzhi, NI Tonghe, WANG Yang, et al. A new approach to the prediction of passenger flow in a transit system[J]. Computers and Mathematics with Applications, 2011, 61: 1968-1974.
[5] 郑辉. 城际铁路客流预测的Logit模型[J]. 铁道运输与经济, 2011, 33(5): 84-87.
ZHENG Hui. Logit model for passenger forecast of inter-city railway[J]. Railway Transport and Economy, 2011, 33(5): 84-87.
[6] 李倩. 基于路网的高速铁路客流预测方法研究[D]. 北京: 北京交通大学交通运输学院, 2001: 87.
LI Qian. Research on passenger flow forecasting method of high-speed railway based on road network[D]. Beijing: Beijing Jiaotong University. School of Traffic and Transportation, 2001: 87.
[7] 夏烈. 基于MD模型的客运专线旅客运量预测方法研究[D]. 西南交通大学交通运输学院, 2011: 64.
XIA Lie. Analysis of passenger traffic forecast methods of passenger dedicated line[D]. Southwest Jiaotong University. School of Traffic and Transportation, 2011: 64.
[8] TIAN Qingfei, ZHAO Shuzhi, CAO Yang. Prediction of station passenger flow volume based on fractal theory[J]. Applied Mechanics and Materials, 2011, 99/100: 203-206.
[9] 王超, 钱进, 李军, 等. 基于时间序列的趋势外推模型预测城市轨道交通车站客流的应用[J]. 铁路计算机应用, 2012, 21(5): 50-55.
WANG Chao, QIAN Jin, LI Jun, et al. Application of trend extrapolation model based on time series in passenger flow prediction of urban transit station[J]. Railway Computer Application, 2012, 21(5): 50-55.
[10] 王芳. 铁路客运量短期预测方法的研究[D]. 北京: 北京交通大学交通运输学院, 2006: 44.
WANG Fang. Research of short-term passenger transportation volume forecasting methods[D]. Beijing: Beijing Jiaotong University. School of Traffic and Transportation, 2006: 44.
[11] 孙晚华, 刘钢. 铁路城际客流预测模型的研究[J]. 北京交通大学学报, 2005, 29(3): 84-87.
SUN Wanhua, LIU Gang. Research on the model of forecasting passenger flow of the intercity train[J]. Journal of Beijing Jiaotong University, 2005, 29(3): 84-87.
[12] 李海军, 张玉召, 朱昌锋. 基于灰色模型及月度比例系数法的铁路客流预测方法[J]. 西部交通科技, 2012(3): 61-64.
LI Haijun, ZHANG Yuzhao, ZHU Changfeng. Railway passenger flow forecasting methods based on grey model and monthly proportion coefficient method[J]. Western China, 2012, (3): 61-64.
[13] 郭义荣, 董宝田. 铁路客运专线客流预测模型研究[J]. 铁路运输与经济, 2011, 33(9): 86-90.
GUO Yirong, DONG Baotian. Study on passenger flow prediction model of railway PDLs[J]. Railway Transport and Economy, 2011, 33(9): 86-90.
[14] Zadeh L A. Fuzzy sets and fuzzy systems[J]. International Journal of General Systems, 1990, 17(2/3): 129-138.
[15] 袁妍, 洪晓光. 基于模糊-粗糙集的移动对象k近邻预测[J]. 计算机科学, 2008, 35(2): 140-143.
YUAN Yan, HONG Xiaoguang. Fuzzy-rough sets for prediction of moving objects’ k-nearest neighbor[J]. Computer Science, 2008, 35(2): 140-143.
[16] James M K, Michael R G and James A G. A fuzzy k-nearest neighbor algorithm[J]. IEEE Transactions on Systems, Man and Cybernetics, 1985, 15(4): 580-585.
(编辑 陈爱华)
收稿日期:2014-03-30;修回日期:2014-05-28
基金项目(Foundation item):国家科技支撑计划项目(2009BAG12A10);国家高技术研究发展计划(863计划)项目(2012AA112001);轨道交通控制与安全国家重点实验室自主研究课题(RCS2009ZT002,RCS2011ZZ004);中央高校基本科研业务费专项资金资助项目(2011JBM161);国家自然科学基金项目(61074151)(Project (2009BAG12A10) supported by the National Science & Technology Pillar Program; Project (2012AA112001) supported by National High Technology Research and Development Program of China (863 Program); Project (RCS2009ZT002, RCS2011ZZ004) supported by Independent Research Project of State Key Laboratory of Rail Traffic Control and Safety; Project (2011JBM161) supported by the Fundamental Research Funds for the Central Universities; Project (61074151) supported by National Natural Science Foundation of China)
通信作者:贾利民(1963-),男,新疆阿勒泰人,教授,从事智能交通系统研究;电话:010-51683824;E-mail:jialm@vip.sina.com