网络首发时间: 2017-09-20 10:03
稀有金属 2018,42(08),791-798 DOI:10.13373/j.cnki.cjrm.xy17050050
含缺陷压铸AlSi9Cu3合金疲劳寿命的计算
陈颖 张峥 Franck Morel
北京航空航天大学材料科学与工程学院
Arts et Métiers ParisTech Laboratoire LAMPA
摘 要：
研究压铸铝合金AlSi9Cu3基体中铸造缺陷和疲劳寿命的关系有望实现铝合金疲劳寿命的预测, 具有较大的工程实用价值。采用Paris公式可以对含缺陷铝合金的疲劳寿命进行计算。然而在现有报道中, 缺陷类型对合金疲劳寿命的影响被忽略, 导致计算的准确性降低。本文在对含缺陷压铸AlSi9Cu3铝合金试样的疲劳寿命测试的基础上, 通过引入缺陷类型的几何因子对Paris公式进行修正, 提高了其计算精度。首先, 通过对试样进行疲劳实验和断口分析, 明确了合金中主要包括3种裂纹:穿透裂纹、表面裂纹和角裂纹。其次, 采用公式计算得到穿透裂纹、表面裂纹和角裂纹的平均几何因子分别为1.421, 0.814和0.947, 其中穿透裂纹对疲劳寿命的影响最大。在此基础上, 采用Paris-Erdogan公式对铝合金的疲劳寿命进行了计算, 计算疲劳寿命与实验疲劳寿命结果相吻合, 计算误差在一倍以内, 证实了假设的合理性和计算的可行性。该计算可以在实际应用中为含缺陷铝合金寿命的预测提供重要的理论基础和实际参考。
关键词：
压铸铝合金;几何因子;Paris公式;疲劳寿命计算;
中图分类号： TG249.2
作者简介：陈颖 (1990-) , 女, 湖北鄂州人, 硕士, 研究方向:压铸铝合金的高周疲劳性能;E-mail:buaachy@126.com;;*张峥, 教授;电话:010-82339485;E-mail:zhangzh@buaa.edu;
收稿日期：2017-05-25
基金：国家科技部重点研发计划项目 (2016YFC0801900) 资助;
Fatigue Life Calculation of Pressure Die Casting AlSi9Cu3 Alloy with Defects
Chen Ying Zhang Zheng Franck Morel
School of Materials Science and Engineering, Beihang University
Laboratoire Arts et Métiers Paris Tech d'Angtrs (LAMPA) , Arts et Métiers Paris Tech Laboratoire
Abstract：
The study on correlations between casting defects and fatigue life in AlSi9Cu3 pressure die-casting aluminum alloys might help to the prediction of aluminum alloys fatigue life, possessing an important practical value. The fatigue life of aluminum alloys with defects could be calculated by Paris' law. However, the effect of defect types on alloys fatigue life was overlooked in past studies, which resulted in the reduction of calculation accuracy. In this paper, on the basis of research on fatigue life of die-cast aluminum alloy with different defects, Paris' lawwas modified by introducing geometric factors of different defect types, improving its calculation accuracy.Firstly, we explicated that alloys consisted of through crack, surface crack and corner crack by analyzing the results of fatigue test.Secondly, the average geometric factors of 1. 421, 0. 814 and 0. 947 were calculated for through crack, surface crack and corner crack, respectively, where through crack showed the greatest influence on fatigue life among three cracks. On this base, fatigue life of aluminum alloys was calculated by Paris-Erdogan formula, where the calculated results could correspond well to test data and the error was between half and twice of calculated fatigue life, confirming the reasonability of hypothesis and feasibility of calculation. This calculation could provide important theoretical basis and practical reference for the prediction of aluminum alloys fatigue life in practical applications.
Keyword：
die-casting aluminum alloys; geometric factor; Paris' law; fatigue life calculation;
Received： 2017-05-25
铸造铝合金因其良好的力学性能和铸造性能在航空航天、建材、汽车等领域有着广泛的应用。随着国家对于节能减排的要求不断提高和汽车轻量化的不断发展, 在汽车的各种零部件中, 铝合金材料占比越来越大, 其中发动机缸盖和缸体等结构材料大量采用压铸铝合金[1,2]。在所有铝合金中 (Al-Si系、Al-Cu系、Al-Mg系铝合金等) , AlSi9Cu3铝合金由于具有比强度高、可铸性强、耐腐蚀性能好以及可循环利用等优点, 目前已经在汽车工业领域中得到广泛应用[3,4]。
目前, 工业上一般采用压铸方法制造铝合金零件, 因为其具有生产效率高, 易实现机械化和自动化等优点[5,6]。然而, 压铸过程可导致铝合金基体中存在大量铸造缺陷, 因此, 在实际工程应用中, 一般通过对铝硅合金铸件进行固溶和时效处理来消除部分缺陷, 以提高材料的机械性能, 但热处理并不能使铸造缺陷完全消除[7,8]。研究表明, 缺陷的位置、形状及尺寸对承载结构件的疲劳寿命及其他力学性能有重要影响[9,10,11]。因此, 压铸铝合金Al Si9Cu3基体中铸造缺陷和疲劳寿命关系的研究有望实现铝合金疲劳寿命的预测, 具有较大的工程实用价值[12]。
目前, 很多研究人员采用Paris-Erdogan公式 (或由其演变的公式) 对裂纹稳态扩展行为进行研究。Madia等[13,14]在Paris-Erdogan公式基础上, 应用Forman-Kearney-Engle公式并对裂纹扩展行为进行了分析, 在该公式中他们考虑了高应力强度因子区域内应力比R的影响, 提高了应力强度因子的计算精度。刘艳萍[15]引入了有效应力强度因子的概念, 并用Elber方程计算了相关疲劳寿命, 进一步提高了应力强度因子的计算精度;赵永翔等[16]提出了一种有效描述门槛值附近和高应力强度因子范围的裂纹扩展速率计算公式, 扩展了Paris-Erdogan公式的使用范围。尽管以上计算方法取得了一定成果, 然而研究人员在计算过程中并没有考虑缺陷类型对合金疲劳寿命的影响, 这可能会影响应力强度因子的计算精度, 进而对疲劳寿命计算的精度产生影响。
本文在对含缺陷压铸Al Si9Cu3铝合金试样的疲劳寿命测试的基础上, 通过引入缺陷类型的几何因子对Paris公式进行修正, 提高了其计算精度。采用修正后的Paris公式计算得到的疲劳寿命与实验疲劳寿命结果相吻合, 计算误差在一倍以内。该计算为工程中含缺陷压铸铝合金疲劳寿命的预测提供了重要参考。
1 实验
本研究使用的实验材料是标志汽车公司提供的发动机缸盖材料压铸Al Si9Cu3合金, 已经过热处理和热变形处理, 材料成分如表1所示, 其屈服强度σy=160 MPa, 弹性模量E=64.5 GPa。
本实验的研究材料是处于平衡态的Al Si9Cu3合金, 其显微金相图如图1所示。从图1中可以看出, 该材料由呈树枝状的α-Al相和呈片状的共晶Si相组成。经测量可知, Al Si9Cu3合金中树枝晶间距约为28μm, 孔隙率为 (3.7±0.5) %, 这种枝晶间距有利于提高合金的力学性能[17]。同时, 从图1中还可以看出合金中存在较多的缺陷 (如图中椭圆标记区域所示) , 这些缺陷主要来自于压力铸造过程中产生的气孔, 疏松和夹杂。其中, 夹杂物主要成分为硅和金属液中包含的其他金属杂质。
为了研究缺陷对于材料疲劳性能的影响, 特加长试样最小横截面积尺寸, 设计为板状等宽试样, 避免疲劳断裂处无缺陷, 试样厚度为 (5.00±0.02) mm, 加工示意图如图2所示。将50组试样经抛光消除表面残余应力后, 以频率30 Hz在Instron 1341万能试验机上进行室温疲劳测试, 其应力比R=-1。试验条件由柴油发动机实际工况决定, 由于本研究中柴油发动机的最大工作压强为160 MPa左右, 而此压铸铝硅合金的疲劳极限约为60 MPa。故疲劳试验的压力水平定为60~160 MPa。试样断裂或应力循环周次达到1×107时终止实验, 记录最终循环周次Nf。实验主要在7个应力 (60, 68, 75, 90, 100, 120, 160 MPa) 水平下进行, 为尽可能在每个应力水平包含几种不同种类的缺陷, 每个应力水平设计了7~9个试样, 应力幅度σα=0.5× (σmax-σmin) 。为保证结果有效性, 对50组试样进行测量, 将测量结果绘制成图3。采用扫描电镜 (SEM, HITACHI 4800) 观察样品断口处的缺陷和裂纹。
表1 压铸合金Al Si9Cu3成分Table 1 Composition of cast alloy Al Si9Cu3 (%, mass fraction) 下载原图
表1 压铸合金Al Si9Cu3成分Table 1 Composition of cast alloy Al Si9Cu3 (%, mass fraction)
图1 压铸Al Si9Cu3合金的显微金相图Fig.1 OM image of die cast Al Si9Cu3
图2 疲劳试样加工示意图Fig.2 Diagram of processed fatigue specimen (mm)
2 结果与讨论
2.1 实验结果分析
图3为压铸铝合金Al Si9Cu3的S-N曲线。从S-N曲线上可以看出, 50组压铸Al Si9Cu3试样的疲劳性能分散性较大, 这可能是由于试样中包含的缺陷种类、尺寸和位置差异较大所导致。在同一应力水平下, 相较于没有缺陷或含有较小缺陷的试样而言, 包含较大的铸造气孔试样的疲劳寿命会显著下降。
图3 含缺陷压铸Al Si9Cu3合金在R=-1下的S-N曲线 (“→”表示1×107应力循环周次后未断裂的试样) Fig.3 S-N curve of pressure die cast Al Si9Cu3alloy with vari-ous defects tested at stress ratio R=-1 (“→”indica-ting run out-sample with no failure up to 1×107cycles)
图4为压铸Al Si9Cu3铝合金的断口处SEM图, 图4中呈现出了3种不同类型的裂纹。通过对50组试样进行观察统计, 发现其中11组试样中呈现出如图4 (a) 中的表面裂纹;20组试样呈现出如图4 (b) 中的表面裂纹;14组试样呈现出如图4 (c) 中的角裂纹 (其中有5组未断裂试样不计入统计) 。因此可以认为, 含缺陷压铸Al Si9Cu3铝合金断口表面的裂纹主要包括穿透裂纹、表面裂纹和角裂纹3种类型。
图5为压铸铝合金3种裂纹的SEM放大图。从图5中可以更加清晰地看到试样中的3种裂纹:穿透裂纹 (图5 (a) ) 、表面裂纹 (图5 (b) ) 和角裂纹 (图5 (c) ) 。此外, 根据SEM图也可测量出3种裂纹的尺寸。根据Gerard和Koss[18]的研究, 由缺陷诱发的初始疲劳裂纹尺寸和原缺陷尺寸在同一个数量级, 故研究过程中以测量得到的缺陷尺寸作为初始疲劳裂纹尺寸ai, 并分别测量3种初始裂纹尺寸。对于穿透裂纹而言, 疲劳条带垂直于缺陷的主方向, 取裂纹半宽度作为裂纹初始尺寸ai, 为了精确测量裂纹宽度, 量取穿透裂纹10个不同区域的宽度, 取平均值计算其裂纹尺寸, 如图5 (a) 所示。统计发现穿透裂纹尺寸分布范围在300~900μm之间。对于表面裂纹而言, 裂纹前沿常为半椭圆形, 通过测量此半椭圆长轴2ci与短半轴ai表征表面裂纹的尺寸, 如图5 (b) 所示。测量发现表面裂纹尺寸的分布范围为200~1200μm。对于角裂纹而言, 裂纹前沿常为四分之一椭圆形, 通过测量此四分之一椭圆长半轴bi与短半轴ai计算其裂纹尺寸, 如图5 (c) 所示, 计算表明角裂纹尺寸分布范围为300~1100μm。上述结果表明, 由于不同样品的裂纹尺寸大小差异明显, 因此在计算疲劳寿命时, 需要将不同样品的裂纹尺寸分别代入进行计算。
图4 3种典型缺陷的SEM图Fig.4 SEM images of three typical fracture
(a) Through crack; (b) Surface crack; (c) Corner crack
图5 3种典型缺陷的SEM放大图及其尺寸测量Fig.5 Magnified SEM images of three typical fracture and size measurement (a) Through crack; (b) Surface crack; (c) Corner crack
2.2 计算结果分析
2.2.1 Paris-Erdogan公式
裂纹发展阶段一般包括裂纹萌生、裂纹扩展和裂纹断裂3个阶段。Paris-Erdogan裂纹扩展经验规律式主要用来描述不同材料和多种试验条件下的疲劳裂纹扩展规律。对于含铸造缺陷的铝合金材料来说, Paris线性扩展区占疲劳寿命的绝大部分。因此, 在计算中假设疲劳裂纹从压铸铝合金试样的缺陷处萌生阶段及最后裂纹快速扩展至断裂阶段可以忽略, 仅考虑裂纹稳态扩展阶段。在以上假设基础上, Paris-Erdogan公式适用于本实验中含缺陷压铸Al Si9Cu3铝合金疲劳行为的研究。
在循环加载条件下, 当载荷所对应的最大应力强度因子远低于准静态断裂韧性时, 就可能从预先存在的裂纹或缺陷处发生裂纹扩展, Paris和Erdogan认为循环加载条件下的裂纹从初始尺寸ai到临界尺寸af的扩展过程服从下述规律[19]:
式中, da/d N是每次载荷循环中疲劳裂纹长度的改变量 (a是裂纹长度, N是疲劳循环周次) ;C和m是经验常数, 取决于材料性能, 微观组织结构, 载荷频率, 平均应力, 载荷比, 加载方式和试验温度等, 可由实验数据拟合得到;ΔKeff是有效应力强度因子范围, 最初由Elber在考虑了裂纹闭合效应后提出,
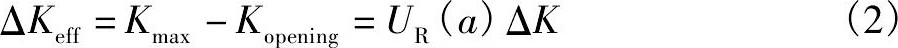
式中, Kmax是最大正应力σmax下的应力强度因子;Kopening是裂纹张开应力强度因子;UR (ai) 是裂纹闭合因子;ΔK可由下式表示,
将有效应力强度因子范围表达式代入Paris公式并积分得,
式中, Y (a) 是裂纹的几何因子。根据先前报道可知[20], 随着裂纹的扩展, Y (a) 相对于am/2这一项增长十分缓慢, 且在等式左边的积分项中, a值较小时对积分值影响较大, 故令Y (a) =Y (ai) 对计算结果带来的误差非常小, 即在计算中采用裂纹萌生时的几何因子替代整个裂纹扩展过程中的几何因子。在本研究的实验过程中, 载荷比R=-1, 假设裂纹闭合效应不出现在疲劳加载的拉伸阶段而只出现在压缩阶段, 即Kopening=0, 则裂纹闭合因子UR (ai) 值为0.5, UR (ai) ×Δσ=0.5×Δσ=σa。
同理, 在裂纹扩展过程中, UR (a) 值的变化也非常有限, 本研究中令UR (a) =UR (ai) , 即在计算中采用裂纹萌生时的几何因子和闭合因子替代整个裂纹扩展过程中的几何因子和闭合因子。
令裂纹从ai扩展至断裂的循环周次为Np=Nf-Ni, 故式 (4) 积分得,
由式 (5) 可知, 疲劳寿命主要受裂纹形状因子和初始裂纹尺寸影响。Gerard等[18]的研究表明, 萌生的初始疲劳裂纹尺寸和缺陷尺寸在同一个数量级。在考虑初始裂纹尺寸的基础上, 铝合金的疲劳寿命主要取决于疲劳裂纹的平均几何因子。因此, 在一定程度上, 疲劳裂纹的几何因子对合金疲劳寿命的影响规律与铸造缺陷对疲劳寿命的影响规律是一致的。
2.2.2 裂纹前沿的几何因子计算
根据ASTM的E647标准, 利用带有预制裂纹的试样进行试验得到位于Paris公式线性区的材料系数值为m=4.116, C=3.745×10-12。在先前的研究中, 一般假设几何因子为1[15,16]。因此, 将本实验测得的试样初始裂纹尺寸代入式 (5) 计算疲劳寿命, 可得合金疲劳寿命计算值Np。图6为合金疲劳寿命计算值Np与实验值Nf对比图, 从图6中可以看出计算结果和实验结果的分散性较大。这表明含不同缺陷种类和不同缺陷尺寸的试样中裂纹前沿几何因子值不同, 因此不能将几何因子简单近似为1, 需要对不同裂纹的几何因子分别进行计算。对于图中小部分计算疲劳寿命稍大于实验疲劳寿命的裂纹, 其几何因子应稍大于1, 大部分裂纹的几何因子值接近1, 其余值略小于1。
图6 计算疲劳寿命与实验结果对比, 假设几何因子为1Fig.6 Comparison of calculated fatigue life (assuming geome-try factor value as 1) with tested number of cycles to failure for all samples
(1) 穿透裂纹前沿几何因子计算
对包含穿透裂纹 (裂纹宽度为2a) 的试样, 其宽度为W, 并假设试样处于弹性变形状态, 施加到试样上的应力值为σ, 可得表达式:
这里, 几何因子Y是无量纲量, 为半裂纹宽度a和裂纹中心距e的函数;KI为I型应力强度因子。
在穿透裂纹中心偏离试样中心时, 根据Liu[21]的研究, 假设裂纹尖端分别为A点和B点, 则它们的几何因子可由式 (7) 表达:
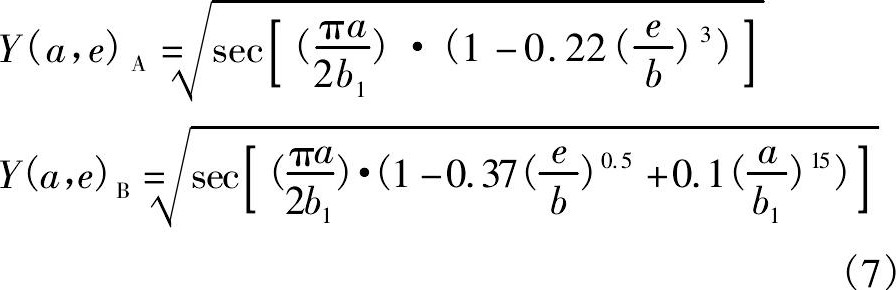
式中, e是裂纹中心偏离试样中心的距离, b是试样半宽度, b1=b-e (裂纹中心与较近试样边缘距离) 。计算时取A点和B点中的最大值作为计算最大应力强度因子时的几何因子值。通过计算所有含穿透裂纹的式样其裂纹扩展初期的几何因子得到几何因子平均值为1.421。
(2) 表面裂纹前沿几何因子计算
根据Newman和Raju[22]对拉弯载荷下含半椭圆形表面裂纹的试样进行的三维有限元分析, 得到单向拉压载荷下, 其应力强度因子经验表达式:
式中, St为单向拉伸应力幅度, a为裂纹深度, 2c为裂纹宽度, 2h, 2b和t分别为试样的长度、宽度和厚度, 且0<a/c≤1.0, 0≤a/t<1.0, c/b<0.5, 
。因此, 表面裂纹的几何因子表达式为
。其中:
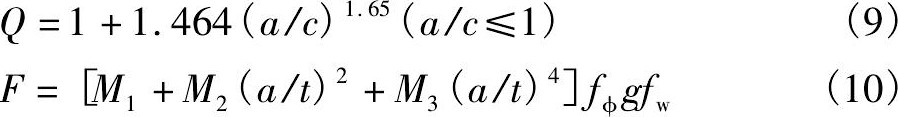
这里, 系数M1, M2, M3及g的表达式如下:
另外, 半椭圆裂纹中的角度函数f的表达式为:
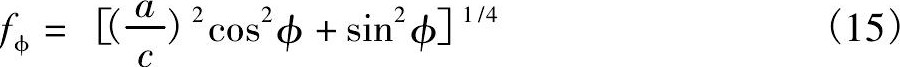
其试样宽度修正函数fw为:
应力强度因子是角度变量Ф的函数, 当a/c<0.6时, 在裂纹最深点Ф=π/2处达到最大应力强度因子;当a/c≥0.6时, 在裂纹与试样表面交界点Ф=0处达到最大应力强度因子[23]。在本实验中, a/c≥0.6, 故最大应力强度因子均出现在Ф=0处。
测量断口上初始裂纹尺寸ai, 2ci, 并根据上述公式, 计算其几何因子。值得注意的是, 疲劳裂纹扩展过程中的几何因子随着裂纹的扩展不断增大, 并在临界裂纹前沿处达到最大值。经计算, 表面裂纹的几何因子平均值为0.814。
(3) 角裂纹扩展几何因子的计算
Kiciak等[24]的研究证明, 在拉压载荷作用下的弹性体中裂纹前沿的应力强度因子K可以由截面上的应力分布函数
与权函数
在裂纹路径Γ上的积分求出。
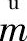
通过在恒应力分布σ (y) 下的权函数计算在A点和C点的应力强度因子 (如图7, 在试样正表面上的裂纹端点为C点, 在试样侧表面上的裂纹端点为A点) , 由于本文研究材料最大应力强度因子值, 故取A点和C点之中较大值。A点和C点的权函数计算公式如下,
故裂纹前沿A点和C点的应力强度因子计算表达式为,
值得注意的是, 如果缺陷离试样角部的距离小于缺陷直径, 则将其尺寸等效处理后, 以角裂纹的理论进行计算。等效方法为测量缺陷在垂直于应力方向上的投影面积, 将其等效为与其具有同等面积和同等短长轴比b/a的四分之一椭圆。经计算, 角裂纹几何因子平均值为0.947。
上述计算表明, 不同裂纹类型的平均几何因子差异较大。其中穿透裂纹的几何因子平均值为1.421, 表面裂纹为0.814, 角裂纹为0.947。它们与之前假设的几何因子1差距较大, 因此不同裂纹类型的几何因子不能简单设定为1。此外, 通过对比可知, 在3种缺陷类型中, 穿透裂纹对疲劳寿命的影响最大, 角裂纹影响次之, 表面裂纹影响最小。
图7 在有限尺寸试样上的角裂纹Fig.7 Corner crack in a finite plate
图8 计算疲劳寿命与实验疲劳寿命对比Fig.8 Comparison of calculated fatigue life by fracture mechanic model with experimental fatigue life (a) Through crack; (b) Surface crack; (c) Corner crack
2.3 计算疲劳寿命与实验疲劳寿命对比
将上述计算得到的3种裂纹的平均几何因子分别代入式 (5) , 可以得到3组疲劳寿命的计算值Np。以实验疲劳寿命Nf为横坐标, 以计算疲劳寿命Np为纵坐标作图可得到图8。图8中实线表示两者完全吻合, 两条虚线分别表示计算疲劳寿命为实验疲劳寿命的1/2和2倍。从图8中可以看出, 计算疲劳寿命与实验疲劳寿命吻合得较好, 计算误差在一倍以内。本研究中共做了3个假设 (或近似) : (1) 假设疲劳裂纹从压铸铝合金试样的缺陷处萌生阶段及最后裂纹快速扩展至断裂阶段可以忽略, 仅考虑裂纹扩展阶段; (2) 在计算中采用裂纹萌生时的几何因子替代整个裂纹扩展过程中的几何因子; (3) 假设裂纹闭合效应不出现在疲劳加载的拉伸阶段而只出现在压缩阶段, 即Kopening=0。计算结果和实验结果的一致性证明这3个假设是可行的。这说明本文中采用的计算方法是合理的, 也表明裂纹类型的几何因子对疲劳寿命的影响不能忽略。因此, 在实际应用中该计算可以为含缺陷铝合金寿命的预测提供重要的理论基础和实际参考。
3 结论
1.通过对50组铝合金的疲劳实验和断口形貌研究, 明确了压铸Al Si9Cu3铝合金在断裂过程中主要存在3种裂纹:穿透裂纹、表面裂纹和角裂纹。
2.通过计算3种裂纹的平均几何因子, 揭示了3种裂纹类型对疲劳寿命的影响规律, 其中穿透裂纹 (Y=1.421) 影响最大, 角裂纹次之 (Y=0.947) , 表面裂纹最小 (Y=0.814) 。
3.在此基础上, 采用Paris-Erdogan公式对铝合金的疲劳寿命进行了计算;计算疲劳寿命与实验疲劳寿命结果相吻合, 计算误差在一倍以内。这表明对含缺陷压铸Al Si9Cu3铝合金试样而言, 裂纹几何因子的引入, 可使其疲劳寿命的计算精度得到明显提高。
参考文献
[1] Liu B, He G Q, Fan K L, Liu X S, She M, Zhu M H.Low-cycle fatigue behavior of cast Al Si9Cu3aluminum alloy[J].Functional Materials, 2014, 45 (4) :04047. (刘斌, 何国求, 樊康乐, 刘晓山, 佘萌, 朱旻昊.铸造铝合金Al Si9Cu3低周疲劳行为[J].功能材料, 2014, 45 (4) :04047.)
[2] Yamagata H, Kasprzak W, Aniolek M, Kurita H, Sokolowski J H.The effect of average cooling rates on the microstructure of the Al-20%Si high pressure die casting alloy used for monolithic cylinder blocks[J].Journal of Materials Processing Technology, 2008, 203:333.
[3] Cho I, Amanov A, Kwak D, Jeong B, Park I.The influence of surface modification techniques on fretting wear of Al-Si alloy prepared by gravity die casting[J].Materials&Design, 2015, 65:401.
[4] Fabrizi A, Ferraro S, Timelli G.The influence of Sr, Mg and Cu addition on the microstructural properties of a secondary Al Si9Cu3 (Fe) die casting alloy[J].Materi-als Characterization, 2013, 85:13.
[5] dos Santos S L, Antunes R A, Santos S F.Influence of injection temperature and pressure on the microstructure, mechanical and corrosion properties of a Al Si Cu alloy processed by HPDC[J].Materials&Design, 2015, 88:1071.
[6] Spangenberger A G, Lados D A, Coleman M, Birosca S, Hardy M C.Microstructural mechanisms and advanced characterization of long and small fatigue crack growth in cast A356-T6 aluminum alloys[J].International Journal of Fatigue, 2017, 97:202.
[7] Sj9lander E, Seifeddine S.The heat treatment of Al-SiCu-Mg casting alloys[J].Journal of Materials Processing Technology, 2010, 210 (10) :1249.
[8] Battaglia E, Bonollo F, Timelli G, Fiorese E, Kral G.Correlation between process, microstructure and properties in high pressure die casting aluminium-silicon alloys[J].Advances in Materials and Processing Technologies, 2017, 3 (1) :111.
[9] Adamane A R, Arnberg L, Fiorese E, Timelli G, Bonollo F.Influence of injection parameters on the porosity and tensile properties of high-pressure die cast Al-Si alloys:a review[J].International Journal of Metalcasting, 2015, 9 (1) :43.
[10] Fiorese E, Bonollo F, Timelli G, Arnberg L, Gariboldi E.New classification of defects and imperfections for aluminum alloy castings[J].International Journal of Metalcasting, 2015, 9 (1) :55.
[11] Kim Y G, Fujii H, Tsumura T, Komazaki T, Nakata K.Three defect types in friction stir welding of aluminum die casting alloy[J].Materials Science and Engineering:A, 2006, 415 (1-2) :250.
[12] Beretta S, Carboni M.Experiments and stochastic model for propagation lifetime of railway axles[J].Engineering Fracture Mechanics, 2006, 73 (17) :2627.
[13] Madia M, Beretta S, Sch9del M, Zerbst U, Luke M, Varfolomeev I.Stress intensity factor solutions for cracks in railway axles[J].Engineering Fracture Mechanics, 2011, 78 (5) :764.
[14] Wei H, Zhao Y X, Zhang Y B.New model for long fatigue crack growth rate[J].Chinese Journal of Mechanical Engineering, 2006, 11:019.
[15] Liu Y P.Study on Fatigue Crack Growth Behavior in Welded Steel Plates Used for Bridges[D].Wuhan:Huazhong University of Science and Technology, 2012.43. (刘艳萍.焊接桥梁钢疲劳裂纹扩展行为研究[D].武汉:华中科技大学, 2012.43.)
[16] Zhao Y X, Yang B, Zhang W H.New model for long fatigue crack growth rate[J].Chinese Journal of Mechanical Engineering, 2006, 42 (11) :120. (赵永翔, 杨冰, 张卫华.一种疲劳长裂纹扩展率新模型[J].机械工程学报, 2006, 42 (11) :120.)
[17] Liao H C, Ding Y, Sun G W.Correlation between mechanical property and characteristic parameters of dendriticαphase in near-eutectic Al-Si alloys modified with strontium[J].Foundry, 2002, 51 (9) :541. (廖恒成, 丁毅, 孙国维.锶变质近共晶Al-Si合金力学性能与枝晶α-Al特征参数的相关性[J].铸造, 2002, 51 (9) :541.)
[18] Gerard D A, Koss D A.Porosity and crack initiation during low cycle fatigue[J].Materials Science and Engineering:A, 1990, 129 (1) :77.
[19] Caton M J, Jones J W, Mayer H, Stanzl-Tschegg S, Allison J E.Demonstration of an endurance limit in cast319 aluminum[J].Metallurgical and Materials Transactions A, 2003, 34 (1) :33.
[20] Wang Q G, Apelian D, Lados D A.Fatigue behavior of A356-T6 aluminum cast alloys.Part I.Effect of casting defects[J].Journal of Light Metals, 2001, 1 (1) :73.
[21] Liu A.Summary of stress-intensity factors[P].US Patent, OH 44073-0002, 1996.
[22] Newman J C, Raju I S.An empirical stress-intensity factor equation for the surface crack[J].Engineering Fracture Mechanics, 1981, 15 (1-2) :185.
[23] Branco R, Antunes F V.Finite element modelling and analysis of crack shape evolution in mode-I fatigue middle cracked tension specimens[J].Engineering Fracture Mechanics, 2008, 75 (10) :3020.
[24] Kiciak A, Glinka G, Eman M, Shiratori M.Weight functions and stress intensity factors for corner quarter-elliptical crack in finite thickness plate subjected to inplane loading[J].Engineering Fracture Mechanics, 1998, 60 (2) :221.
