J. Cent. South Univ. Technol. (2008) 15(s1): 084-087

DOI: 10.1007/s11771-008-320-4

Displacement of polymer solution on residual oil trapped in dead ends

ZHANG Li-juan(张立娟)^{1, 2}, YUE Xiang-an(岳湘安)^{1, 2}

(1. Key Laboratory of Petroleum Engineering of Ministry of Education, China University of Petroleum,

Beijing 102249, China;

2. Enhanced Oil Recovery Research Center, China University of Petroleum, Beijing 102249, China)

Abstract: For waterflooding reservoir, oil trapped in pore’s dead ends is hardly flushed out, and usually becomes one typical type of residual oil. The microscopic displacement characteristics of polymer solution with varied viscoelastic property were studied by numerical and experimental method. According to main pore structure characteristics and rheological property of polymer solution through porous media, displacement models for residual oil trapped in dead ends were proposed, and upper-convected Maxwell rheological model was used as polymer solution’s constitutive equation. The flow and stress field was given and displacement characteristic was quantified by introducing a parameter of micro swept coefficient. The calculated and experimental results show that micro swept coefficient rises with the increase of viscoelasticity; for greater viscoelasticity of polymer solution, vortices in the dead end have greater swept volume and displacing force on oil, and consequently entraining the swept oil in time. In addition, micro swept coefficient in dead end is function of the inclination angle (θ) between pore and dead end. The smaller of θ and 180-θ, the flow field of viscoelastic fluid is developed in dead ends more deeply, resulting in more contact with oil and larger swept coefficient.

Key words: polymer flooding; micro displacement mechanism; viscoelastic; residual oil

1 Introduction

After waterflooding, residual oil may exist in different forms^[1-2], which is related to the structure of porous media, surface wettability, and the properties of oil and water as well as displacement situation. In intermediate wet and oil wet cases, residual oil exists in the form of oil column trapped in small pores called dead ends. In recent year, displacement of residual oil trapped in dead end by polymer flooding is of special interest. Many phenomena are observed that viscoelastic effects are favorable to oil mobilization in microscopic experiments^[3-4]. The comparison experiments of water, glycerin, and partially hydrolyzed polyacrylamide (HPAM) solution have been done on glass-inched micro model by WANG et al^[3]. Glycerin and HPAM solution are regarded as viscous and viscoelastic respectively. It has been found that the latter can further improve the displacement efficiency after glycerin flooding. Although qualitative analysis^[5-11] on some observations has been made, however, there is still lack of quantitative correlation between displacement behavior and viscoelasticity. Besides, the mechanism involved in controlling the displacement behavior need to be detailed understood. The work discusses how polymer solution with varied viscoelastic property affect flow field in dead end and its displacement characteristics. In general, pore structure is very complicated, dead end is not always vertical to pore, and the inclination angle may vary between 0^o-180^o. The impacts of inclination angle on flow and displacement were studied.

2 Mathematical models

2.1 Governing equations

In oilfields, partially hydrolyzed polyacrylamide (HPAM) is one of the most widely used polymers, which can be treated as viscoelastic flow in porous media. Assuming that the second normal stress is negligible, the upper-convected Maxwell constitutive equation can be used to describe the rheological behavior of a viscoelastic fluid. The displacement model of residual oil trapped in dead end is shown in Fig.1. In the displacement model, the inclination angle (θ) between pore and dead end varies from 0^o to 180^o arising from the complicated pores’ structure.

The steady incompressible plane flow of a viscoelastic fluid is governed by the continuity equation:

                                 (1)

The momentum equations are:

             (2)

             (3)

The constitutive equations are:

                                      (4)

                                 (5)

                                    (6)

where  u and v denote velocity in the x and y direction, respectively, p denotes pressure, denotes shear stress, anddenote normal stresses, denotes density, denotes relaxation time, and 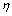 denotes zero-shear viscosity.

Fig.1 Residual oil in dead end and its displacement model

2.2 Numerical method

The finite difference method used is essentially that of COCHRANE et al^[12-13], with the modification of non-uniform mesh size. Eqn.(1) through Eqn.(6) is written in stream function-vorticity formulation with the pressure variable eliminated. The nonlinearly coupled matrix systems are solved in turn by using under-relaxation iteration and Gauss-Seidel iteration.

3 Results and discussion

3.1 Flow field

Flow fields of polymer solution are shown in Fig.2, while We is equal to either 0 or 0.2. We referred as We=λU/L, is a dimensionless parameter, measuring the magnitude of viscoelasticity, the larger the We, the greater the viscoelasticity. Where U is the average velocity in the main channel, and L is the length of model. Streamline in main channel is spaced out 0.2 apart, and in dead end 0.005 apart. It can be seen by comparison of Figs.2(a) and 2(b) that with the increase of We, the vortices center move to dead end deeply, and the velocity increases. With inclination angle approaching 90?, the velocity in dead end decreases.

To mobilize the residual oil, two premises are essential. One is that displacing fluids reach the positions where residual oil is trapped. The other is that the driving force on residual oil is large enough to conquer the resistance. Flow fields of polymer solution, as shown in Fig.2, indicates that with the increase of viscoelasticity, polymer solution can contact more oil, thus, it has larger swept volume.

Fig.2 Flow fields in pores with dead end (Re=0.001): (a) We=0, θ=90?; (b) We=0.2, θ=90?; (c) We=0, θ=120?; (d) We=0.2, θ=120?

3.2 Stress field

In order to depict acting forces imposed on oil when polymer solution flowing, modulus of deviatoric stress tensor Q is introduced to characterize the comprehensive action of shear stress and normal stress, which is referred

as 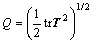. Where, T denotes deviatoric stress tensor.

It can be seen from Fig.3, with the increase of We, the level line Q=0.2 moves to the deeper part of dead end, and the stress imposed to the fluid within the dead end increases. In addition, the inclination angle θ has great impact on stress field, and with θ far from 90?, stress on fluid in dead end gets greater.

Fig.3 illustrates that with the increase of viscoelasticity, the driving force provided by polymer solution gets stronger. Residual oil trapped in dead end is displaced in the following way. Vortex is developed more deeply to contact more oil; moreover, vortex, which is of great stress, disperses residual oil into movable oil ganglia, and finally carries them into the main channels.

3.3 Comparison with experimental results

Fig.4 shows experimental results for two kinds of viscoelastic polymer solution displacing residual oil trapped in the dead ends on micro glass-inched models

Fig.3 Contour lines of modulus of deviatoric stress tensor in pores with dead end (Re=0.001): (a) We=0, θ=60?; (b) We=0.2, θ=60?; (c) We=0, θ=90?; (d) We=0.2, θ=90?; (e) We=0, θ=120?; (b) We=0.2, θ=120?

Fig.4 Displacement experiment for xanthan gum solution We=0.052(a) and HPAM solution We=0.26(b)

after waterflood. It is observed that, viscoelastic xanthan solution can drive part of residual oil in dead ends after waterflood, and HPAM solution with greater viscoelasticity can make more residual oil flushed out after xanthan solution flooding. Comparison with the above numerical results indicates that there is good agreement between numerical results and experimental ones, which suggests that with the increase of viscoelasticity, the micro swept volume is enlarged and the driving force is larger enough to conquer the resistance. The resistance which includes viscous resistance and structural stress on crude oil is denoted as τ₀. Combined the numerical and experimental results, the displacement characteristics of polymer solution on residual oil trapped in dead ends can be furtherly quantified.

3.4 Micro swept coefficient

According to Von Mises yield conditions, when the modulus of deviatoric stress tensor is greater than τ₀, residual oil trapped in dead ends can be entrained to the main stream, that’s Q＞τ₀. The rheological experiments indicates, under the reservoir flow conditions, dimensionless yield stress of crude oil is ranging between 10^-3 and 10^-1. As a special case, the contour of modulus of deviatoric stress tensor when Q=τ₀=0.2 is given. Take the level line Q=0.2 as the displacement boundary, the micro swept coefficient of residual oil in dead ends, denoted as Se, can be calculated by

where  f(Q) is the position function of level line Q=0.2, andis the depth of dead end.

Fig.5 gives the micro swept coefficient of residual oil in dead ends as a function of We and θ. The micro-sweep efficiency, as shown in Fig.5 begins to increase rapidly with the increase of We at a wide range of favorable inclination angle, say, 20?＜θ＜160?, and becomes excellent as θ→90?. On the other hand, when the inclination is unfavorable, θ≤20? or θ≥160?, the micro swept coefficient is substantially inferior to that achieved for 20?＜θ＜160? with the same We, and improves little with the increase of We. The micro swept coefficient of polymer solution presented in Fig.5(b), regardless of viscoelastic effects, becomes smaller with inclination angle approaching 90?. Thus, it implies that the viscoelastic effect on improving micro swept coefficient only work on residual oil of dead ends with inclination angle say, 20?＜θ＜160?.

Fig.5 Micro swept coefficient vs We with Re=0.001(a) and micro swept coefficient vs θ with Re=0.001(b)

4 Conclusions

1) Swept volume of polymer solution in the dead ends is determined by its flow field and stress field. With the increase of viscoelasticity, vortex in dead end is developed more deeply to contact more oil; moreover, it is of greater stress, and disperses more residual oil into movable oil ganglia, and finally carries them into the main channels.

2) The inclination angle between pore and dead end has great effects on flow field and stress field. With inclination angle approaching 90?, the velocity and stress in dead end decreases.

3) Micro swept efficiency enlarges with the increase of viscoelasticity, at a wide range of inclination angle, say, 20?＜θ＜160?, and becomes excellent as θ→90?. The displacement potential of viscoelastic polymer flooding on residual oil trapped in dead ends increases when inclination angle approaching 90?.

References

[1] TONG Zheng-shin, YANG Cheng-zhi, WU Guo-qing, YUAN Hong, YU Li, TIAN Gen-lin. A study of microscopic flooding mechanism of surfactant /alkali/polymer[C]// SPE/DOE Improved Oil Recovery Symposium. Tulsa, 1998: SPE/DOE 39662.

[2] YAN Qing-yan, GONG Wen-chao, JIA Zhong-wei. Mechanism of asp flooding in Daqing oil field[J]. Petroleum Geology & Oilfield Development in Daqing, 1999, 18(3): 24-26. (in Chinese)

[3] WANG De-min, CHENG Jie-cheng, YANG Qing-yan, CONG Wen-chao, LI Qun, CHEN Fu-ming. Viscous-elastic polymer can increase microscale displacement efficiency in cores[C]// SPE Annual Technical Conference and Exhibition. Dallas, 2000: SPE63227.

[4] WANG De-min, CHENG Jie-cheng, XIA Hui-fen, LI Qun, SHI Jing-ping. Improvement of displacement efficiency of cores by driving forces parallel to the oil-water interface of viscous-elastic fluids[J]. Acta Petrolei Sinica, 2002, 23(5): 48-52. (in Chinese)

[5] PYE D J. Improved secondary recovery by control of water mobility[J]. JPT, 1964, 16(8): 911-916.

[6] SANDIFORD B B. Laboratory and field studies of water floods using polymer solutions to increase oil recoveries[J]. JPT, 1964, 16(8): 917-922

[7] DAUBEND D L Jr, MENZIE D E. Flow of polymer solutions through porous media[J]. JPT, 1967, 19(8): 1065-1073.

[8] MOHAMMAD R, JUERGEN R, GUENTER P, RUEDIGER M. Quantification and optimization of viscoelastic effects of polymer solutions for enhanced oil recovery[C]// SPE/DOE Enhanced Oil Recovery Symposium. Tulsa, 1992: SPE/DOE 24154.

[9] HESTER R D, FLESHER L M, MCCORMICK C L. Polymer solution extension viscosity effects during reservoir flooding[C]// SPE/DOE Improved Oil Recovery Symposium. Tulsa, 1994: SPE/DOE 27823.

[10] HAN X Q, WANG W Y, XU Y. The viscoelastic behavior of HPAM solutions in porous media and it’s effects on displacement efficiency[C]// International Meeting on Petroleum Engineering. Beijing, 1995: SPE 30013.

[11] KONG Fan-shun, WANG Xiu-lian, XIA Hui-feng. Microcosmic displacement mechanism of viscoelastic polymer solution displacing the residual oil at the dead end[J]. Petroleum Geology & Oilfield Development in Daqing, 2007, 20(5): 110-113. (in Chinese)

[12] COCHRANE T, WALTERS K, WEBSTER M F. Newtonian and non-newtonian flow near a reentrant corner[J]. J Non-Newt Fluid Mech, 1982, 10: 95-114.

[13] CROCHET M J, DAVIES A R, WALTERS K. Numerical simulation of non-newtonian flow[M]. New York: Elsevier Science Publisher B V, 1984: 85-120.

(Edited by YANG You-ping)

Foundation item: Project(50574060) supported by the National Natural Science Foundation of China; Project(2005CB221300) supported by the National Basic Research Program of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: ZHANG Li-juan, PhD, Lecturer; Tel: +86-10-89733552; E-mail: zhangljbj2001@sina.com