Trans. Nonferrous Met. Soc. China 27(2017) 608-615

Sequential multi-objective optimization of thin-walled aluminum alloy tube bending under various uncertainties

Heng LI¹, Jie XU¹, Heng YANG¹, He YANG¹, Guang-jun LI²

1. State Key Laboratory of Solidification Processing, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China;

2. Chengdu Aircraft Industry (Group) Corporation Ltd., Chengdu 610092, China

Received 29 January 2016; accepted 30 August 2016

Abstract: Combining the design of experiments (DOE) and three-dimensional finite element (3D-FE) method, a sequential multi- objective optimization of larger diameter thin-walled (LDTW) Al-alloy tube bending under uncertainties was proposed and implemented based on the deterministic design results. Via the fractional factorial design, the significant noise factors are obtained, viz, variations of tube properties, fluctuations of tube geometries and friction. Using the virtual Taguchi’s DOE of inner and outer arrays, considering three major defects, the robust optimization of LDTW Al-alloy tube bending is achieved and validated. For the bending tools, the robust design of mandrel diameter was conducted under the fluctuations of tube properties, friction and tube geometry. For the processing parameters, considering the variations of friction, material properties and manufacture deviation of mandrel, the robust design of mandrel extension length and boosting ratio is realized.

Key words: robust optimization; tube bending; uncertainty; aluminum alloy; multi-objective optimization

1 Introduction

Larger diameter thin-walled (LDTW) aluminum alloy (Al-alloy) bent tubes, as key “bleeding” transforming components, have attracted increasing usage in several fields such as aviation and aerospace [1]. Among many bending approaches, mandrel bending is preferable to realize bending of LDTW Al-alloy tubes with good repeatability. However, the mandrel bending of LDTW Al-alloy tube is a triple nonlinear process. The features of large diameter and low elongation make the bending of LDTW Al-alloy tube much sensitive to the changes of forming parameters, viz, tooling parameters and processing parameters.

To realize precision bending, the strict coordination of various bending tools and forming parameters should be achieved via the deterministic optimization. While, there exist many uncontrollable variables induced by material fabrication processes, tooling manufacturing and bending processes, which may influence the bending quality and forming efficiency. Thus, it is urgently needed to obtain the knowledge on effects of the uncertainties on bending and to achieve the multi- objective robust design of forming parameters for mandrel bending of LDTW Al-alloy tubes.

Many studies have been done on different tube bending processes of various tubular materials. However, most studies focus on the effects of forming parameters on individual defect and few on deterministic optimization, saying nothing of robust design considering uncontrollable variables in bending [1-4]. The tooling setup was designed by the fuzzy logic through tube properties and geometry of bending [5]. Using design of experiments (DOE) and FE methods, XU et al [6] conducted the deterministic optimization of mandrel parameters for LDTW Al-alloy tube bending. Considering multiple defects, LI et al [7] developed a knowledge-based substep method to solve the multi- objective deterministic optimization of LDTW Al-alloy tube bending. However, whether the optimal results by the deterministic design work robustly in mandrel bending of Al-alloy tube is questionable. Robust optimization has become a promising and important technology in product design [8,9]. BAGCHI [8] discussed the Pareto-optimal robust design for solving the multi-objective design problems by genetic algorithms (GA). Using multi-objective particle swarm optimization method, SUN et al [9] presented a multi- objective robust Pareto design to consider the roles of uncertainties on draw bead optimization, in which the variations were obtained by the six sigma principle and the surrogate model was formulated by a dual response surface method (RSM). These studies provide the method references for robust design of LDTW Al-alloy tube bending.

This study attempts to develop a suitable method for multi-objective robust design of tube bending under fluctuations in Al-alloy tubes bending process. First, the significance or sensitive analysis of fluctuating factors on multi-index constraining bending quality is conducted via the fractional factorial design and 3D-FE simulation. Then, considering the significant noise factors, the robust optimization design of both tooling parameters and processing parameters are performed using virtual Taguchi’s DOE of inner and outer arrays. The experiments are done to verify the robust design methods.

2 Experimental

2.1 Forming parameters and bending quality

As shown in Fig. 1, under multi-tool constraints, the unequal plastic forming occurs during bending, viz, the tension deformation at extrados and compression mode at the intrados. With inappropriate conditions, there may occur wrinkling instability, over thinning (or even fracture) and cross-sectional distortion. The inherent nonlinearity of LDTW Al-alloy tube bending makes its optimization a multi-objective problem with multiple variables and constraints [10-13].

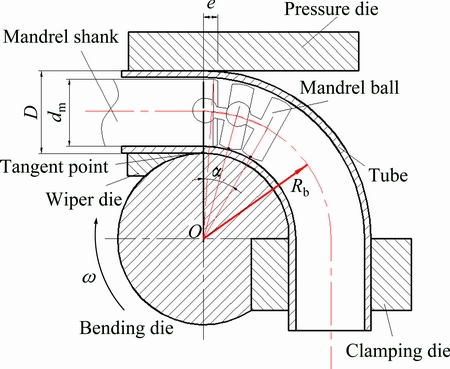
Fig. 1 Schematic of mandrel bending

Equations (1)-(4) show the indexes for bending quality, viz, wall thickness changing degree (thinning T and thickening T_k), cross-section flattening degree Q and wrinkling wave height W. The larger the values of the above indices, the worse the bending quality becomes. Generally, T should be less than 25%, Q should be less than 15% and W should be less than 2%D.

T=(t₀-t_min)/t₀×100%                       (1)

T_K=(t_max-t₀)/t₀×100%                      (2)

Q=(D₀-D_min)/D₀×100%                       (3)

W=D₁-D₂                                   (4)

where D₀ is out diameter; t₀ is original wall thickness; t_min and t_max are the minimum and maximum thicknesses after bending; D_min, D₁, D₂ are the minimum tube diameter after bending, the maximum and minimum section diameter of tube after bending, respectively.

2.2 3D-FE modeling and verification

Figure 2 shows that the whole bending procedure of LDTW Al-alloy tube is modeled based on the Abaqus Explicit/implicit algorithms. The detailed modeling issues can be found in Refs. [6,10]. The experiments are conducted to verify the established 3D-FE model.

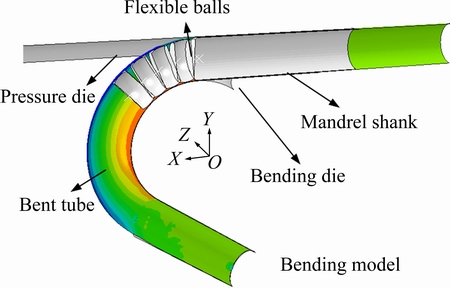
Fig. 2 3D-FE model for mandrel bending

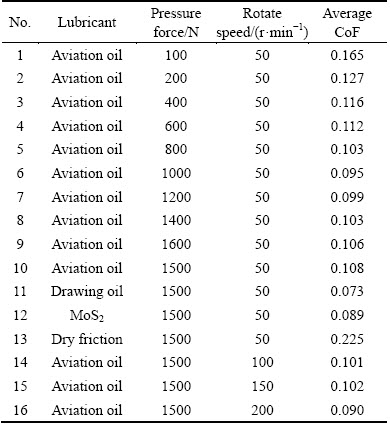
The bending specification is 5052O d50 mm ×1 mm × 75 mm (D × t × R_b, R_b/D=1.5, where R_b is the bending radius; D is the outer diameter of tube). By uniaxial tension tests, the material properties can thus be obtained as shown in Fig. 3. The twist-compression test (TCT) [14] was used to reproduce the friction conditions between tube and bending tools, and the normal anisotropy exponent is calculated by the ratio of the width strain to thickness strain (see Table 1).

The strain hardening law is 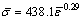. Table 2 shows the simulation conditions. Figure 4 shows that the numerical results can reveal the bending characteristics. The maximum deviation is less than 15%. The unconformity is mostly induced by the property variations, friction conditions and instability of loading conditions such as pressure die movements.

2.3 Orthogonal design of experiment

Robust design is a method that uses DOE to improve the robustness of product manufacturing.

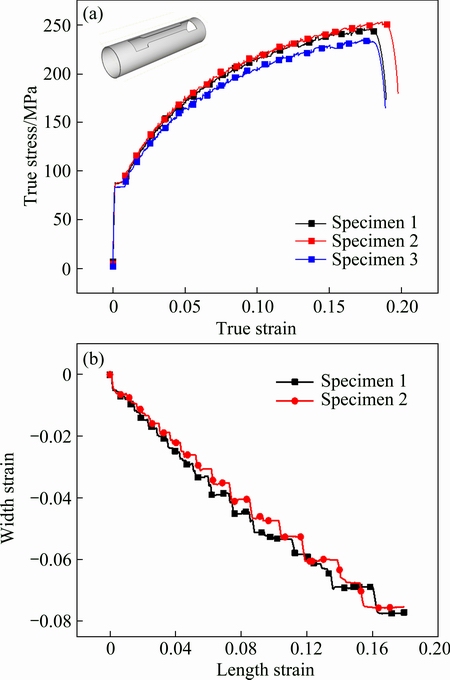
Fig. 3 Variation of properties of 5052O seamless tube

Table 1 Coefficient of friction (CoF) under different tribological conditions

1) Analysis of parameter design

Select the quality characteristic y, and identify the factors, then judge whether the function between the factors and y can be determined: If yes, to obtain the function; If not, to obtain the influence tendency.

Table 2 Simulation parameters for Al-alloy tube bending

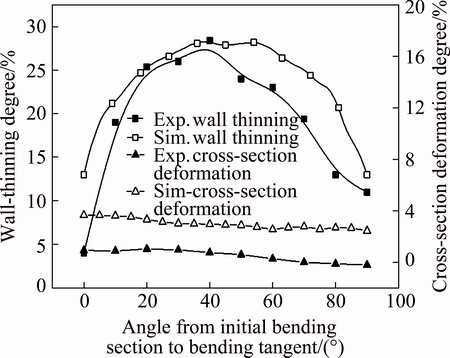
Fig. 4 Comparison between FE and experimental results

2) Determination of noise factors

The factors whose levels are difficult or expensive to be controlled are called noise factors, which are the root cause of the fluctuation of y.

3) Design for Taguchi’s DOE of inner and outer arrays

Put all controllable factors on an orthogonal table, and this table is called inner table; Put all noise factors on another table, and this table is called outer table.

4) Experimental result y_ij

If there are m level combinations in outer table and n level combinations in inner table, Taguchi’s design needs m × n tests, and we can obtain m × n quality characteristic value y_ij (i=1, 2, …, m; j=1, 2, …, n).

5) Index of inner table

The n data in inner table can be noted as y₁, y₂, …, y_n, the average value as 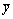, and the variance as s². The signal noise ratio (SNR) is used as the index for inner table. The equations of the SNR are different from each other for different quality characteristics [15].

The nominal-the-better characteristic:

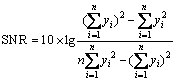                 (5)

The smaller-the-better characteristic:

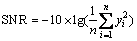                       (6)

The larger-the-better characteristic:

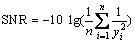                       (7)

6) Statistical analysis

Take the calculated SNR from outer table as the index for inner table, and conduct the statistical analysis on SNR using the orthogonal design, viz, direct analysis and variance analysis. The following judgments should be conducted, viz, which controllable factors have significant impact on the increasing tendency of SNR; which level combinations of controllable factors are the best or the most satisfactory to reduce the fluctuation; If the fluctuation is not reduced to a satisfactory level, to make a choice whether the second-round test is needed or not and it needs to extract the trend information of factors from the previous tests.

3 Results and discussion

3.1 Sequential multi-objective robust optimization methodology

3.1.1 Selection of design factors

For the controllable variables, the mandrel diameter is thought to be the most significant tooling parameter in bending [10,16], and both the mandrel extension length e and the boosting ratio K_vp are the most significant processing parameters. These three parameters should be concerned in the robust design.

There are many fluctuations such as friction, clearance, tube properties and geometries [17]. For the clearance, the variation of the tube geometry is the source of the fluctuation. To reduce the design difficulty, the factorial design method is used to obtain the significant noise factors.

The design of experiment (DOE) is conducted. Nine processing parameters are concerned, viz, f_p (0.25-0.45); clearance between pressure die and tube, c_p (0.05-0.20 mm); f_w (0.05-0.20); clearance between wiper die and tube, c_w (0.05-0.20 mm); f_b (0.25-0.45); clearance between bending die and tube, c_b (0.05-0.20 mm); f_m (0.05-0.20); e (2.00-7.00 mm); K_vp (1.00-1.20). Figure 5 shows the standardized effect of processing parameters on both T and Q. Both friction variations and clearance variations have complex effects on the bending quality and, both c_w and f_m are the most significant noise factors.

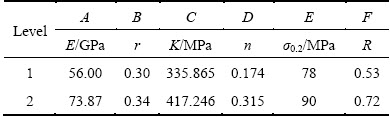
The Plackett-Burman method of DOE is used to find out the significant noise factor about material properties. Table 3 shows the levels of 5052O Al-alloy material parameters such as elastic modulus E, Poisson ratio v, strength coefficient K, strain-hardening exponent n, initial yield strength σ_0.2, normal anisotropy exponent R. As shown in Fig. 6, by direct analysis and statistic analysis, both n and R are the major noise factors in the consequent robust optimization.

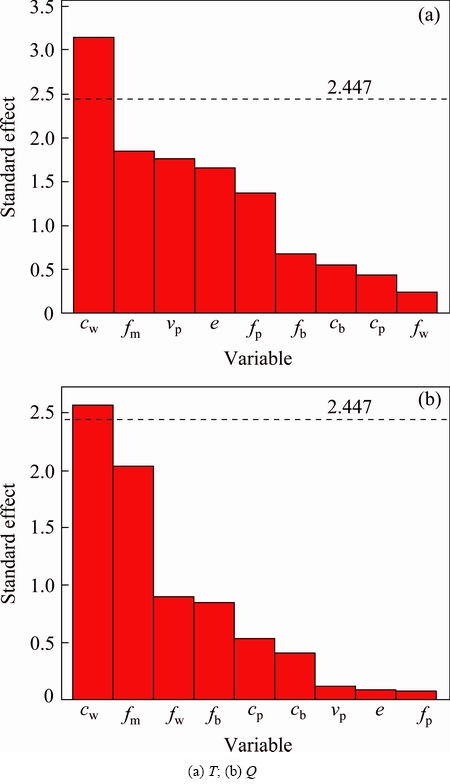
Fig. 5 Pareto plots for processing parameters for responses

Table 3 Levels of material parameters for virtual DOE

3.1.2 Sequential robust optimization methodology

Figure 7 shows the proposed sequential multi- objective robust design methodology for Al-alloy tube bending.

1) Determine the fluctuation range of the friction factor, and then design the robust design arrays.

2) Analyze the SNR, and obtain the optimal d_m that makes the SNR largest.

3) Consider the fluctuation range of the material properties, the robust design of d_m is conducted.

4) Determine the fluctuation range of tube dimensions, and conduct the robust design of d_m.

5) Establish 3D-FE models to calculate the multi- objective function values as Eqs. (1)-(4).

6) Consider the fluctuation of f_m, d_m and the material properties as the noise factors, to design the robust design arrays.

7) Change input files of the FE models and analyze SNR, to obtain the optimal values of e and K_vp.

8) Compare the results of robust design with those of deterministic design, and obtain the forming parameters which enable more stable forming.

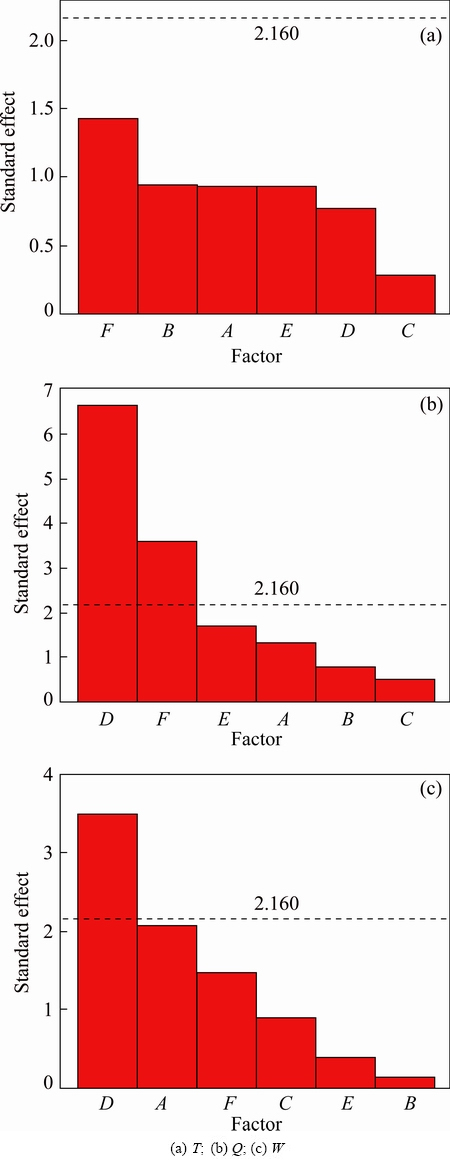
Fig. 6 Pareto plots for material properties for responses

3.2 Multi-objective robust design of processing parameters

3.2.1 Robust design of mandrel diameter

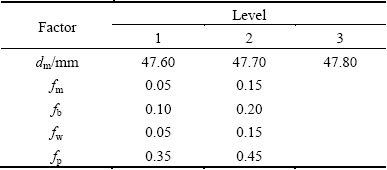
The levels of d_m and CoFs are selected as listed in Table 4. The noise factors of CoFs in the outer table are arranged by the orthogonal experimental design L₈(2⁷), and the level of the inner table is determined based on the deterministic optimization results [7]. The design of the inner and outer tables and the FE-based results are shown in Table 5.

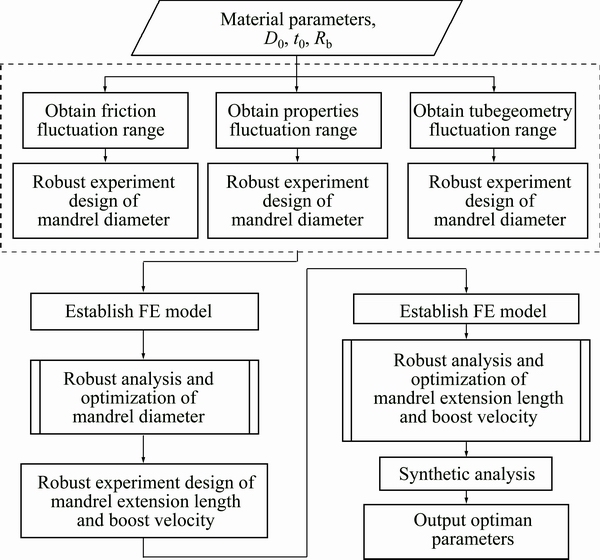
Fig. 7 Process flow of sequential multi-objective robust optimization design under uncertainties

Table 4 Levels of factors for robust design of d_m

Based on the results from Taguchi inner and outer table arrays and the smaller-the-better feature, we calculate the SNR of different mandrel diameters under the noise factors-the fluctuation of the friction conditions by Eq. (6). The robustness of the selection of d_m is judged by the SNR. The larger the SNR is, the stronger the anti-disturbing capability of the selected d_m becomes, and thus the more stable the bending forming quality is. Table 6 shows the calculation results of SNR for the different levels of mandrel diameter under variations of CoFs. In Table 6, SNRT, SNRTK, SNRQ, and SNRW are the SNRs of the smaller-the-better features with the T, T_K, Q, and W as bending responses, respectively.

For d_m of 47.70 mm, taking the maximum T as the response, the SNR of d_m is the maximum under the fluctuations of CoFs. Taking the maximum W as the response, the SNR is the maximum for d_m of 47.70 mm under friction variations. Therefore, the robust requirements can be achieved with d_m of 47.70 mm.

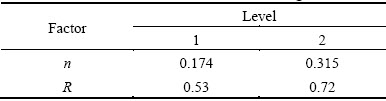
The robust optimization of d_m is conducted only considering two material properties, viz, n and R. Table 7 shows the selected levels of the material parameters. The orthogonal table L₄(2³) is used in outer table. Via the smaller-the-better characteristic, the robust design results are obtained. Table 8 shows that, with d_m of 47.60 mm and taking the T as the target, the forming quality is more robust; when d_m equals 47.70 mm and taking Q as the target, the cross-section quality is more robust; with d_m of 47.70 mm and taking W as the target, the forming quality is more robust.

Table 5 Taguchi’ design of inner and outer table for mandrel diameter d_m considering fluctuation of friction factors

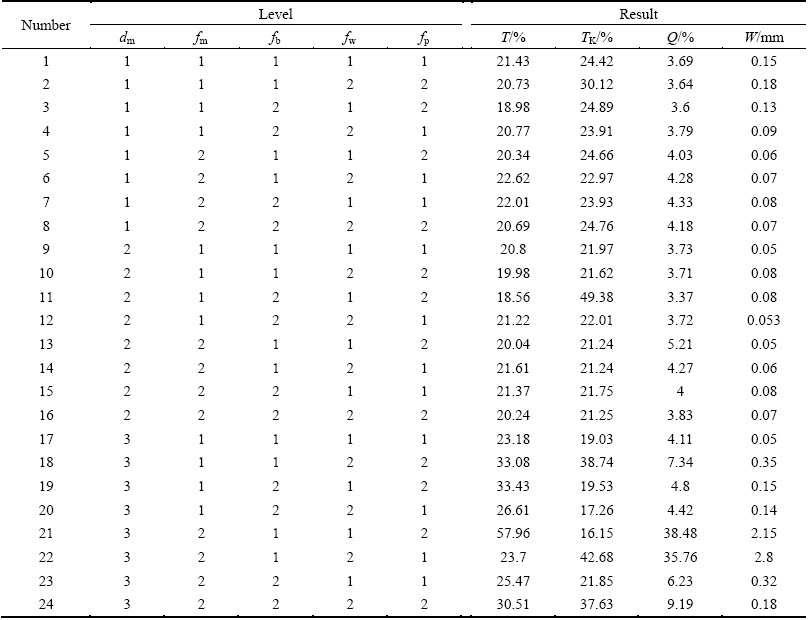
Table 6 Calculated results for robust design of d_m considering fluctuation of friction factors

Table 7 Levels of material factors for robust design

For 50 mm × 1 mm × 75 mm Al-alloy tube, 30 tubes are measured. The average of D₀ is 49.91 mm, and the standard deviation σ is 0.2179; the average t₀ is 1.02 mm, and the standard deviation σ is 0.0331. Three- level orthogonal test is used as shown in Table 9. The orthogonal table L₉(3²) is used in outer table. The range of d_m is from 47.40 to 47.60mm. If d_m is greater than 47.60 mm, the mandrel cannot be inserted into the tube. The influence of d_m on the bending quality is obtained. The more the mandrel diameter, the larger the SNR for all forming targets. Thus, the largest d_m should be selected with allowed thinning degree.

By the above analysis and comparison, we can conclude that d_m has different effects on T, T_K, Q and W under the influence of the noise factors. The smaller d_m can reduce the wall thinning degree and cross-section flattening degree of the tube. The reason for this is that the smaller d_m can decrease restriction effect on the tube from the mandrel and the wiper die, thus decreasing the outside tangential strain of the tube.

Table 8 Calculated results for robust design of mandrel diameter considering fluctuation of material factors

Table 9 Levels of factors for robust optimization considering fluctuation of tube geometry parameters

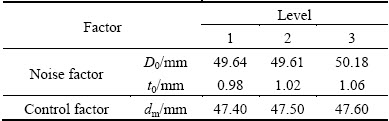
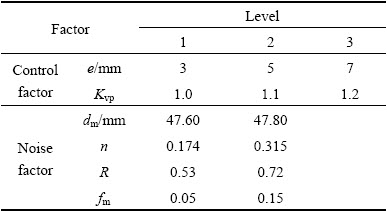
Table 10 Parameter levels for design of processing parameters

3.2.2 Robust optimization of processing parameters

The fluctuations of d_m, n, R and f_m are regarded as the noise factors to design Taguchi’s inner and outer arrays for optimization of processing parameters, viz, e and K_vp.

The level of the noise factor in outer table is 2, and the orthogonal table L₈(2⁷) is chosen. In inner table, both the levels of e and K_vp are 3, and the orthogonal table L₉(3⁴) design is employed as shown in Table 10. There are 72 tests. The direct analysis is used to obtain the robust design of e and K_vp.

From synthetic analysis and comparison, e and K_vp have little effect on T under the fluctuations of the noise factors. Taking the minimum Q as the target, the larger e and the smaller K_vp are, the greater the SNR is, and the more stable the forming becomes (Fig. 8(a)). The reason is that the larger e can provide effective supporting role to decrease section flattening degree. The smaller K_vp can avoid section flattening caused by wrinkle. Taking the minimum W, the smaller the K_vp is, the more stable the forming quality is, but e has little effect on wave height (in Fig. 8(b)). It should be noted that the smaller K_vp can reduce the boosting effect of the pressure die, thus decreasing the inside compressive strain of the tube resulting in less wrinkle trend. The forming quality becomes more stable when e is 7 mm and K_vp equals 1. When e takes the upper bound value of the forming range, K_vp of one can satisfy the requirements of the forming quality, and make forming stable. A series of bending experiments are conducted under the obtained forming conditions. As shown in Fig. 8(c), the qualified LWTD Al-alloy bent tubes can be achieved with T less than 25% and Q less than 10%. The wrinkling is avoided.

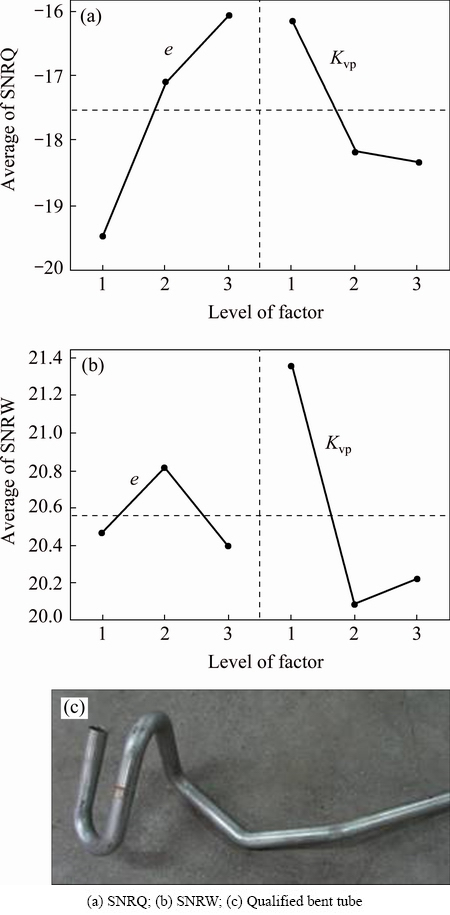
Fig. 8 Main effect of control factors and qualified bent tube

4 Conclusions

1) The analysis for significance of forming factors on multi-index constrained bending quality is performed via fractional factorial design, and the significant noise factors among various uncertainties are obtained.

2) Using virtual Taguchi’s DOE of inner and outer arrays, considering three major defects, the robust optimization designs of the tooling and the processing factors are achieved, respectively.

3) The results show that the bending quality is more stable when the boosting ratio is 1 and the mandrel extension length is upper bound value. The results are successfully applied for the industrial scenario with bending specification of LDTW Al-alloy tube 50 mm × 1 mm × 75 mm.

References

[1] YANG He, LI Heng, ZHANG Zhi-yong, ZHAN Mei, LIU Jing, LI Guang-jun. Advances and trends on tube bending forming technologies [J]. Chinese Journal of Aeronautics, 2012, 25(1): 1-12.

[2] WU Wen-yun, JIN Li, DONG Jie, PENG Li-ming, YAO Shou-shan. Bending mechanisms in AM30 alloy tube using a rotary draw bender [J]. Materials and Manufacturing Processes, 2010, 25: 1359-1364.

[3] LI Heng, HU Xiao, YANG He, LI Long. Anisotropic and asymmetrical yielding and its distorted evolution: Modeling and applications [J]. International Journal of Plasticity, 2016, 82: 127-158.

[4] LAZARESCU L. Effect of internal fluid pressure on quality of aluminum alloy tube in rotary draw bending [J]. International Journal of Advanced Manufacturing Technology, 2013, 64(1-4): 85-91.

[5] STRANO M. Automatic tooling design for rotary draw bending of tubes [J]. International Journal of Advanced Manufacturing Technology, 2005, 26(7-8): 733-740.

[6] XU Jie, YANG He, ZHAN Mei, LI Heng. Design and optimization of mandrel parameters for thin walled aluminum alloy tube NC bending [J]. Materials Research Innovations, 2011, 15(1): s365-s369.

[7] LI Heng, YANG He, XU Jie, WANG Dan, LI Guang-jun. Knowledge-based substep deterministic optimization of large diameter thin-walled Al-alloy tube bending [J]. International Journal of Advanced Manufacturing Technology, 2013, 68(9): 1989-2004.

[8] BAGCHI T P. Multiobjective robust design by genetic algorithms [J]. Materials and Manufacturing Processes, 2003, 18(3): 341-354.

[9] SUN Guang-yong, LI Guang-yao, GONG Zhi-hui, GUI Xiang-yang, YANG Xu-jing, LI Qing. Multiobjective robust optimization method for drawbead design in sheet metal forming [J]. Materials & Design, 2010, 31(4): 1917-1929.

[10] LI Heng, YANG He, ZHAN Mei, SUN Zhi-chao, GU Rui-jie. Role of mandrel in NC precision bending process of thin-walled tube [J]. International Journal of Machine Tools and Manufacture, 2007, 47(7-8): 1164-1175.

[11] LI Heng, YANG He, ZHANG Zhi-yong, LIU Nan, LI Guang-jun, WELO T. Multiple instability-constrained tube bending limits [J]. Journal of Materials Processing Technology, 2014, 214: 445-455.

[12] MA Jun, YANG He, LI Heng, WANG Dan, LI Guang-jun. Tribological behaviors between commercials pure titanium sheet and tools in warm forming [J]. Transactions of Nonferrous Metals Society of China, 2015, 25: 2924-2931.

[13] ZHANG Xiao-li, YANG He, LI Heng, ZHANG Zhi-yong, LI Long. Warm bending mechanism of extrados and intrados of large diameter thin-walled CP-Ti tubes [J]. Transactions of Nonferrous Metals Society of China, 2014, 24(10): 3257-3264.

[14] YANG He, LI Heng, ZHAN Mei. Friction role in bending behaviors of thin-walled tube in rotary-draw-bending under small bending radii [J]. Journal of Materials processing Technology, 2010, 210: 2273-2284.

[15] REN Lu-quan. Optimum design and analysis of experiments [M]. Beijing: Higher Education Press, 2003: 426. (in Chinese)

[16] LI Cheng, YANG He, ZHAN Mei, XU Xu-dong, LI Guang-jun. Effects of process parameters on numerical control bending process for large diameter thin-walled aluminum alloy tubes [J]. Transactions of Nonferrous Metals Society of China, 2009, 9: 668-673.

[17] XU Jie, YANG He, LI Heng, ZHAN Mei. Significance-based optimization of processing parameters for thin-walled aluminum alloy tube NC bending with small bending radius [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 147-156.

不确定因素下薄壁铝合金管弯曲的多目标连续稳健优化设计

李 恒¹，许 杰¹，杨 恒¹，杨 合¹，李光俊²

1. 西北工业大学 凝固技术国家重点实验室，西安 710072；2. 成都飞机工业(集团)有限责任公司，成都 610092

摘  要：结合实验设计和三维弹塑性有限元，在确定性优化设计基础上，提出了不确定因素下薄壁铝合金管数控弯曲的多目标连续稳健优化方法。基于部分析因设计，获得了显著的噪声因子，包括管材性能变化、管材几何尺寸波动和管材-模具摩擦波动。采用田口内外表试验法，考虑主要弯曲成形缺陷，对薄壁铝管数控弯曲芯模直径、芯棒伸出量和助推速度进行了稳健优化设计。通过分别考虑摩擦接触条件、管材料参数和管材几何参数的波动，实现了薄壁铝管数控弯曲芯模直径的稳健性优化设计；通过考虑材料参数波动、芯模与管间的摩擦波动以及芯模直径的制造偏差，实现了芯棒伸出量和助推速度的稳健性优化设计。

关键词：稳健优化；管材弯曲；不确定因素；铝合金；多目标优化

(Edited by Xiang-qun LI)

Foundation item: Project (51275415) supported by the National Natural Science Foundation of China; Project (51522509) supported by the National Science Fund for Excellent Young Scholars, China

Corresponding author: Heng LI; Tel: +86-29-88460212; E-mail: liheng@nwpu.edu.cn

DOI: 10.1016/S1003-6326(17)60068-2