粒子群优化的多机器人协作定位方法

刘利枚^{1, 2}，蔡自兴¹

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；

2. 湖南商学院 计算机与电子工程学院，湖南 长沙，410205)

摘要：针对异质多机器人具有不同的感知能力和处理能力的特点，提出一种基于粒子群优化的多机器人协作相对定位方法。该方法将常规粒子滤波方法与粒子群优化算法有机结合，通过粒子群优化方法对预估粒子进行更新，同时利用多机器人之间的相对观测信息，调整粒子的提议分布和粒子权重，增强多机器人位置预测的有效性，提高多机器人定位的精度。实时数据实验结果表明：该方法正确、可行。

关键词：粒子群优化；粒子滤波；多机器人；协作定位

中图分类号：TP242.6           文献标志码：A         文章编号：1672-7207(2011)03-0682-06

Multi-robot cooperative localization based on particle swarm optimization

LIU Li-mei^{1, 2}, CAI Zi-xing¹

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. School of Computer and Electronic Engineering, Hunan University of Commerce, Changsha 410205, China)

Abstract: According to different perceptions and processing abilities of heterogeneous robots, an approach to multi-robot cooperative localization was presented based on particle swarm optimization. Through the particle swarm algorithm combined with the standard particle filter, the prediction of particles was updated, and the proposal distribution and the weight of particles were adjusted based on the relative observations to enhance the effectiveness of the position prediction and improve the localization accuracy. The online experimential results prove that the improved method is correct and feasible.

Key words: particle swarm optimization; particle filter; multi-robot; cooperative localization

机器人定位是机器人研究领域中的热点问题之一。为了实现移动机器人路径规划、导航、决策和执行任务，要求机器人必须先感知环境，对自己进行准确定位。而与单个机器人相比，多机器人协作定位^[1-5]对于多机器人系统协作运行具有高效、高精度、高容错性、高鲁棒性等优点，因而更适用于各种复杂的任务。目前，一些研究者提出了很多协作定位的方法，如：Roumeliotis等^[6]通过卡尔曼滤波(Kalman fliter, KF)估计多机器人中每个机器人的位置信息(包括相对坐标、相对方位)，然后，把集中的KF分成n个单独的KF，进行分布式处理。该方法成功地应用于室内环境。针对室外非结构化环境，Raj等^[7]利用外围传感器全球定位系统(Globe positioning system, GPS)提出基于扩展卡尔曼滤波(Extend Kalman filter, EKF)的分布式协作定位方法。该方法提高了定位的精度，但实现比较复杂。Dieter等^[8]应用马尔科夫定位方法提出了当一个机器人观测到另一个机器人时，融合机器人的运动信息、环境感知信息和相互观测模型，更新每个机器人的位置，从而实现多机器人的相互定位，但彼此探测时忽略了探测信息的相互依赖，有可能导致过分乐观的位置估计。Andrew等^[9-10]利用粒子滤波器(Particle filter, PF)对机器人队伍进行相对定位。每个机器人以自身的坐标系为基准，通过网络中信息传播及坐标变换来确定队列中其他每个机器人相对自身的位置，即使有些机器人没有被直接观测到，它也能够确定其相对位置。由于不考虑绝对位置，这种方法比较适合于未知的、非静态的环境。在该方法中，每个机器人都维护n-1个粒子滤波器(n为机器人个数)。但是，随着机器人个数的增加，每个机器人所要维护的粒子滤波器数量也不断增加，其计算复杂度以指数级增长，影响了定位的实时性和实用性。王玲等^[11-13]将粒子滤波和扩展卡尔曼滤波相结合提出了一种多机器人合作定位的方法。该方法结合了粒子滤波器的鲁棒性、适应性与EKF的高效率和实时性，使机器人群中各成员可共享全局定位信息, 从而能有效地在未知环境中确定自身的位置，但使用GPS进行全局定位，实现成本高。已经应用的各种定位算法中大致分为卡尔曼滤波和粒子滤波2类。在此，本文作者在粒子滤波的基础上，充分利用异质多机器人中某一机器人的精确定位能力，将粒子群优化算法引入到粒子滤波方法中，得出一种粒子群优化的粒子滤波算法，以实现多机器人的相对定位。与传统的方法相比，该方法融合相对观测量对粒子滤波预测采样过程和粒子的权重进行优化，加速了粒子集收敛，从而增强了位置预测的准确性。

1  相对观测信息的获取

为了实现异质机器人的相互定位，进行以下假设：

(1) 每个机器人都配有运动感知传感器，每个机器人之间都能进行信息交换。

(2) 异质多机器人中存在能力较强的高配机器人，该机器人装配有能够测量其他机器人相对距离和方向的外部传感器，且该机器人能够进行精确自定位。低配的机器人装配有能测量相对位置的外部传感器。

(3) 每个机器人能检测到其他机器人，并且每个机器人的身份识别总是准确无误的。

观测量的获取分为3个阶段：首先，每个机器人根据运动模型，由内部传感器感知它的运动状态，得到机器人移动的距离和方向变化；然后，高配的机器人直接测量附近可探测到的机器人的相对位置，将其他机器人的位置转换到自己的局部坐标中，计算相对观测量；最后，高配机器人把自己观测到的相对位置信息广播给其他机器人，其他机器人通过处理这些信息得到所有观测到和观测不到的机器人相对于自己的距离和方向。

假设若干个机器人组成的队列在环境中探索，其中能精确定位机器人至少1个。用表示机器人在某一时刻的位置，则所有机器人在某时刻的位置可以表示为。机器人之间的相对位置如图1所示。

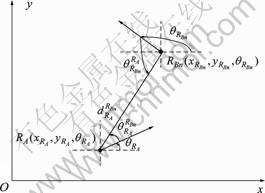
图1  2个机器人之间的相对观测量

Fig.1  Relative observation between two robots

       (1)

        (2)

其中：R_A和R_Bn分别为观测者(高配机器人)和被观测者(低配机器人)在某一时刻的位置；为机器人R_Bn相对于R_A的距离；和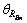分别为R_A和R_Bn的方向角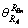；为R_Bn相对于R_A的方向角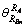；为R_A相对于R_Bn的方向角。

2  融合相对观测量的粒子群优化协作定位算法

基于粒子滤波的同时定位与建图方法，机器人的位置估计是从运动模型中采样获得的，因此，无法根据最新的观测对机器人位置进行更新，导致机器人位置偏离了实际位置，为此，提出一种融合相对观测量的粒子群优化(Particle swarm optimization, PSO)协作定位算法。具有高配的每个机器人都维护一个粒子集合。机器人通过传感器获取相对观测量，利用粒子群优化的粒子滤波方法，估计机器人路径轨迹的后验概率分布，生成预测粒子集，计算粒子权重，估计机器人组中每个机器人的位置，从而提高了多机器人定位的精度和效率。

粒子群优化算法(PSO)^[14-15]是一种基于群体智能的全局优化算法，它利用m个粒子组成的粒子群在n维目标搜索空间中搜索最优解。粒子i具有2个属性：位置x_i=(x_i1, x_i2, …, x_in)^T与速度v_i=(v_i1, v_i2, …, v_in)^T，其中x_i为所求问题的1个潜在解。粒子x_i记录它经历过的最好位置(个体最优位置)p_pbest=(p_i1, p_i2, …, p_in)^T和它的所有领域个体经历过的最好位置(全局历史最优位置) p_gbest=(p_g1, p_g2, …, p_gn)^T。每次迭代中，粒子i第d维的速度和位置按下列表达式更新：

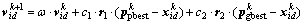   (3)

               (4)

其中：d=1, 2, …, n，为搜索空间维数；i=1, 2, …, m，为粒子总数；k为当前进化代数；r₁和r₂为分布于[0, 1]之间的随机数；c₁和c₂为加速常数；ω为惯性权重。

在基本PF算法中，机器人下一时刻的位置预测是将t-1时刻的第i粒子的位置信息通过控制量u_t对机器人的新位置进行采样获得，并把新的位置写入t时刻的粒子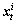中，如下式所示：

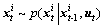              (5)

从式(5)发现：这一预测过程没有考虑到t时刻的最新观测信息，因而无法根据最新的观测信息对机器人预测位置进行及时更新。本文通过观测值对预测采样过程进行优化，提出一种融合相对观测量的粒子群优化协作定位算法。

首先，使用粒子群算法中的速度与位置方程对机器人的预测位置进行更新。更新方程如下：

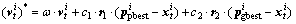   (6)

              (7)

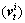式中：和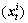分别为粒子i在t时间的速度和位置。通过更新，机器人的位置向量由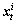变成。

然后，引用适应度函数来判断机器人预测位置的优化程度。该适应度函数定义如下：

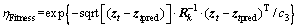  (8)

其中：R_k表示机器人的测量噪声协方差矩阵；c₃为常数；z_t表示t时刻的观测信息；z_tpred表示 t 时刻机器人对被观测者的预测信息。z_tpred可通过预测位置值和已经观测到的位置l­_i计算得到：

              (9)

设定1个阈值δ，当η_Fitness≥δ时，表明该预测值已分布在机器人真实位置附近；反之，则表明该预测值偏离了机器人真实位置。通过以上优化过程使得粒子集趋向于高似然区。

根据上述分析，完整的粒子群优化多机器人协作定位算法如表1所示。

表1  融合相对观测量的粒子群优化多机器人协作定位算法

Table 1  Particle swarm optimized multi-robot cooperative localization obtained by fusing relative observation

3  实验及分析

3.1  协作定位实验结果

为了验证融合相对观测量的多机器人PSOPF定位方法的有效性，实验分别采用里程计估计位置方法、PF单机器人定位方法、多机器人PF定位方法与本文提出的PSOPF方法，在5 m×5 m的实验环境中运行。机器人B采用自行改造的MORCSⅡ，该移动机器人配备有2个传感器和8个声纳。机器人A采用自行设计并研制的MORCS-1，系统装配了1个360脉冲/转增量式光电编码器构成的里程计、E-Core RD1100系列的数字光纤陀螺仪、CXTILT02E/02EC 倾角传感器等内部传感器测量机器人的位姿，利用SICK公司生产的LMS291激光雷达、摄像头作为外部传感器感知机器人之间的距离和相对方向信息，该感知系统能够实现俯仰与水平的二维运动。实验采用的算法重要参数为：c₁=1.5，c₂=1.2，c₃=35，ω=0.7，m=100。

在运动过程中注意保持与机器人A的相对距离不要过大，以便能准确识别其他机器人并获得相对观测量。首先机器人A与2个机器人B₁和B₂做匀速同向直线运动，且初始朝向角为0°，使用本文的方法，实际轨迹和参考轨迹如图2(a)所示(其中，实线为参考轨迹即机器人的真实运动轨迹，虚线为利用本文方法协作定位后的实际估计轨迹)。以机器人B₁为例，机器人定位误差见图3(a)。图3(a)中里程计所估计的最大误差为0.53 m；由PF算法所得的单机器人定位误差为0.27 m；由PF多机器人协作定位误差为0.16 m；由PSOPF多机器人协作定位误差为0.12 m。然后，机器人做匀速折线运动，实际估计轨迹和参考轨迹如图2(b)所示，B₁的定位误差如图3(b)所示。图3(b)中机器人B₁里程计所估计的最大距离误差为0.65 m；由单机器人 PF算法所得最大距离误差为0.45 m；由PF多机器人协作定位所得最大距离误差为0.32 m；由PSOPF多机器人协作定位算法所得最大距离误差为0.29 m。

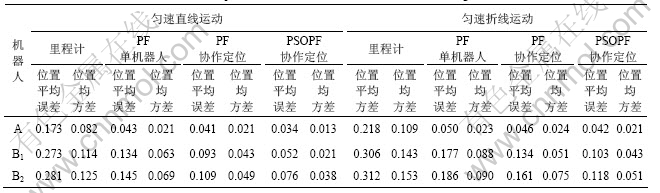
为进一步验证算法的性能，分别采用3种算法计算20次。表2所示分别为4种算法在直线和折线运动下的定位平均误差和方差。

3.2  实验结果分析

从图2可以看出：高配机器人A定位精度比机器人B定位精度高；当机器人朝向角发生变化时，实际估计轨迹会突然偏离参考轨迹，位置估计误差会增大；但随着方向角不变，很快又收敛到机器人的真实位置，位置估计误差逐渐减小。总体来说，使用本文方法所得实际估计轨迹和参考轨迹基本一致。

在机器人运动过程中，位姿估计主要受里程计和机器人速度的影响。从图3和表2可以看出：当机器人B方向角不变且匀速运动时，其里程计测量误差较小且基本保持恒定，因此，根据里程计测量值计算得到的位姿估计误差随时间增加而逐渐增大。采用本文所提出的方法，机器人B的初始阶段定位误差比较大，随着高配机器人利用观测信息进行协作定位后，机器人B逐渐向真实位置靠近，误差逐渐减小。当机器人在折线匀速运动中方向角变化时，系统误差或者位置误差突然增大；当方向角不变时，机器人逐渐稳定，位置误差变化较小。

从以上实验结果可以看出：利用相对观测量的PSOPF方法，与单机器人PF和多机器人PF算法相比，其定位精度有很大提高。

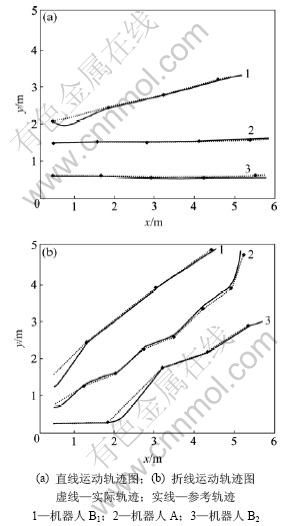
图2  机器人在xOy坐标轴中的实际轨迹和参考轨迹

Fig.2  Motion real trajectory and reference trajectory in xOy coordinate

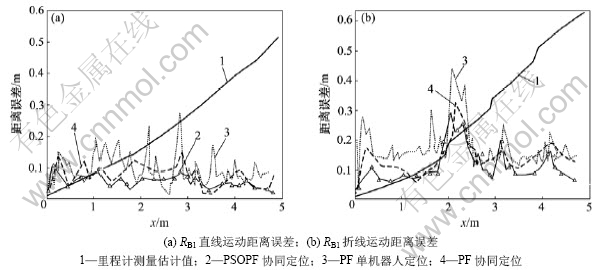
图3  定位误差结果

Fig.3  Localization error

表2  2种不同运动方式的距离误差比较

                      Table 2  Comparison of distance errors for two different running modes                    m

4  结论

(1) 基于粒子滤波的同时定位与建图方法中，针对机器人的位置估计没有根据最新的观测对机器人位置进行更新问题，融合较精确定位的机器人实时观测与其他成员的相对观测量，利用粒子群优化的粒子滤波器，完成了多机器人的相对定位，形成了一个精度高的定位系统。最后通过实验和实时数据，验证了该方法有效、可行。

(2) 该方法适用于由多个小型低配机器人和能力特别强的高配机器人组成的异质多机器人系统。

参考文献：

[1] Zhang L, Rene Z, Pascal l. Self-adaptive Monte Carlo for single-robot and multi-robot Localization[C]//Proceedings of the IEEE International Conference on Automation and Logistics. Shengyang, China, 2009: 1926-1953.

[2] Luca C, Miguel K N, Jing J D, et al. Rao-blackwellized particle filter multi-robot SLAM with unknown initial correspondences and limited communication[C]//2010 IEEE International Conference on Robotics and Automation. Alaska, USA, 2010: 243-250.

[3] CHEN Hao-yao, SUN Dong, YANG Jie. Localization strategies for indoor multi-robot formations[C]//2009 IEEE International Conference on Advanced Intelligent Mechatronics. Singapore, 2009: 1218-1224.

[4] Nikolas T, Stergios I, Roumeliotis, et al. Cooperative multi-robot localization under communication constraints[C]// IEEE International Conference on Robotics and Automation. Kobe, Japan, 2009: 4394-4401.

[5] 蔡自兴, 陈白帆, 王璐, 等. 异质多移动机器人协同技术研究的进展[J]. 智能系统学报, 2007, 2(3): 1-7.
CAI Zi-xing, CHEN Bai-fan, WANG Lu, et al. The progress of cooperative technology for heterogeneous multiple mobile robots[J]. CAAI Transaction on Intelligent System, 2007, 2(3): 1-7.

[6] Roumeliotis S I, Bekey G A. Distributed multirobot localization[J]. IEEE Transactions on Robotics and Automation, 2002, 18(5): 781-795.

[7] Raj M, Kingsley F, Lynne E P. Distributed cooperative outdoor multirobot localization and mapping[J]. Autonomous Robots, 2004, 17(1): 23-29.

[8] Dieter F, Wolfram B, Hannes K, et al. A probabilistic approach to collaborative multi-robot localization[J]. Autonomous Robots, 2000, 8(3): 325-344.

[9] Andrew H, Maja J M, Gaurav S S. Putting the ‘I’ in ‘Team’: An ego-centric approach to cooperative localization[C]//Proceedings of the IEEE International Conference on Robots and Automation. Taipei, 2003: 868-874.

[10] Andrew H. Multi-robot simultaneous localization and mapping using particle filters[J]. International Journal of Robotics Research, 2006, 25(12): 1243-1256.

[11] 王玲, 万建伟, 刘云辉, 等. 基于PF-EKF的多机器人合作定位方法[J]. 中国科学E辑: 信息科学, 2007, 37(12): 1544-1555.
WANG Lin, WAN Jian-wei, LIU Yun-hui, et al. Multi-robot cooperative localization based on PF-EKF[J]. Science in China Series E: Information Science, 2007, 37(12): 1544-1555.

[12] 王玲, 邵金鑫, 万建伟, 等. 多机器人定位中基于熵的分布观测量选择方法[J]. 电子学报, 2007, 35(2): 333-337.
WANG Lin, SHAO Jin-xin, WAN Jian-wei, et al. Distributed entropy based relative observation selection for multi-robot localization[J]. Acta Electronic Sinica, 2007, 35(2): 333-337.

[13] 王玲, 刘云辉, 万建伟, 等. 基于相对方位的多机器人合作定位算法[J]. 传感技术学报, 2007, 20(4): 794-800.
WANG Lin, LIU Yun-hui, WAN Jian-wei, et al. Multi-robot cooperative localization based on relative bearing[J]. Chinese Journal of Sensors and Actuators, 2007, 20(4): 794-800.

[14] Kennedy J, Eberhart R. Particle swarm optimization[C]// Proceedings of the IEEE International Conference on Neural Networks. Perth Western, Australia: IEEE Service Center, 1995: 1941-1948.

[15] Riccardo P, James K, Tim B. Particle swarm optimization an overview[J]. Swarm Intelligence, 2007, 1(1): 33-57.

(编辑 陈灿华)

收稿日期：2010-06-11；修回日期：2010-08-21

基金项目：国家自然科学基金重大专项资助项目(90820302)；国家博士点基金资助项目(200805330005)；国家自然科学基金面上(青年)基金资助    项目(60805027)；中南大学自由探索计划项目(2010)

通信作者：刘利枚(1975-)，女，湖南宁乡人，博士研究生，副教授，从事人工智能研究；电话：13647313360；E-mail: seagullm@163.com