基于AEPSO优化的神经网络多步预测控制
侯志祥1, 2,吴义虎2,袁松贵1, 2,申群太1
(1. 长沙理工大学 汽车与机械工程学院,湖南 长沙410076;
2.中南大学 信息科学与工程学院,湖南 长沙 410083)
摘 要:为提高神经网络预测控制的性能,提出了基于自适应扩展粒子群优化的神经网络预测控制方案。基本PSO算法中,每个粒子的更新受粒子个体极值和局部极值的影响,为了提高其全局收敛性,采用多粒子策略,使每个粒子的更新受更多其他粒子的影响;为提高收敛速度,采用自适应策略,对参数c0进行自适应调整,使c0随着迭代次数的增加而逐渐减小,这样,在PSO算法的搜索过程中,随着迭代次数的增加,搜索区域会越来越小,从而加快PSO算法收敛速度。运用该算法实现神经网络预测控制中的滚动优化,在有限时域内对控制序列进行寻列,给出基于粒子群优化的神经网络预测控制系统的稳定性证明。仿真结果表明,基于粒子群优化的神经网络预测控制系统具有良好的跟踪性能。
关键词:预测控制;神经网络;粒子群优化;收敛性
中图分类号:TP273 文献标识码:A 文章编号:1672-7207(2007)06-1162-07
Multi-steps predictive control of neural networks based on
AEPSO optimization
HOU Zhi-xiang1, 2, WU Yi-hu2, YUAN Song-gui1, 2, SEN Qun-tai1
(1. College of Automobile and Mechanical Engineering, Changsha University of Science and Technology,
Changsha 410076, China;
2. School of Information and Science Engineering, Central South University, Changsha 410083, China)
Abstract: In order to enhance the index of neural network predictive control, a neural network predictive control method was provided by using a self-adaptive expand PSO algorithm. Each particle was refreshed by using individual and local extremum in the basic PSO algorithm. To improve the global convergence, particle was refreshed by multi-particle strategy; at the same time, the parameter c0 was self-adaptively adjusted and in such a way c0 gradually decreased with the increase of iterative time, as the searching area of the PSO algorithm was reduced and the convergence velocity of PSO algorithm was effectively improved. The improved PSO was used as the optimizer of the neural network predictive control and optimized the control serial in the finite time field. The stability of predictive control of neural network using improved PSO as optimizer is proved. Simulation results show that the method has better track performance.
Key words: predictive control; neural network; part swarm optimization; convergence
预测控制对不确定性环境具有良好的适应能力和较强的鲁棒性,成为当今具有广泛应用价值和广阔应用前景的先进控制策略[1-2]。神经网络因具有并行处理、分布式存储以及很好的鲁棒性和自适应、自学习的特性,在控制领域得到广泛应用。神经网络预测控制是将神经网络与预测控制结合构造的新的控制方法,预测模型的精度和滚动优化策略是影响其控制性能的核心[3-4]。Sorensen等[5-6]用BP神经网络构造多步预测模型并采用梯度下降法修正控制律,由于BP神经网络是全局修正网络,因此,学习速度慢,而且以梯度法求取的控制律存在陷入局部极值点的可能。Shin等[7-8]采用具有全局优化特点的遗传算法作为滚动优化的方法,邹健等[9]提出了以小脑模型网络作为多步预测模型,以启发式遗传算法作为滚动优化方法。由于遗传算法在后期的收敛速度慢,因此,其实时控制性能较差。XIAO等[10]提出了以RBF网络作为预测模型,以基本PSO算法作为滚动优化的方法。为进一步改善基于PSO优化的神经网络预测控制的性能,本文作者提出一种用径向基神经网络建立系统去误差直接多步预测模型,用自适应扩展粒子群优化算法进行滚动优化的神经网络预测控制方法。
1 自适应扩展粒子群算法
1.1 自适应扩展粒子群优化算法模型
粒子群优化(Particle swarm optimization,PSO)算法来源于鸟群捕食行为的研究,是一种通用的启发式搜索技术。粒子通过跟踪“个体极值”和“局部极值”来更新自己在解空间中的空间位置与飞行速度。基本PSO算法中,每个粒子的更新受粒子个体极值和局部极值的影响。为了提高其全局收敛性,采用多粒子策略,使每个粒子的更新受更多其他粒子的影响。同时,为提高收敛速度,对参数c0进行自适应调整。随着迭代次数的增加,c0逐渐减小,搜索区域会越来越小,从而加快PSO算法的收敛速度。这种考虑多粒子影响和自适应控制参数的PSO算法合作模型称为自适应扩展粒子群优化(Adaptive expand particle swarm optimization,AEPSO)算法。

将式(1)与基本PSO算式比较可知,粒子根据最优的m个个体极值粒子和最优的n个局部粒子更新自己的速度和位置。由于这种搜索区域的减小趋势不是呈线性减小[11-13],因此,控制参数c0按式(3)进行自适应调整,c0的具体取值是在调试时反复比较之后确定的,a=0.6,b=1。AEPSO 算法充分考虑了更多粒子在迭代寻优过程中包含的信息,算法的全局收敛性更强,同时,由于自适应调整控制参数c0,使得随着迭代代数的增加,搜索区域会越来越小,从而加快收敛速度。
1.2 自适应扩展粒子群优化算法的收敛性分析
AEPSO算法考虑更多粒子值包含的信息用于粒子迭代寻优,必须保证控制参数的选择使得算法具有收敛性。以下通过证明AEPSO算法的收敛性条件,导出AEPSO算法的控制参数设置策略。AEPSO算法的递推计算公式如下。
将式(1)代入式(2),并且根据式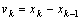 ,可得递推公式:
,可得递推公式:
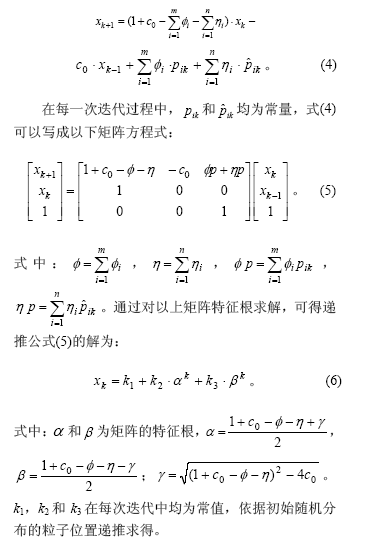
由式(6)可得:
a. AEPSO算法收敛及 为常量的条件为:当
为常量的条件为:当 时,
时,
 ;若满足条件
;若满足条件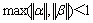 时,可保证AEPSO算法是收敛的。因为当
时,可保证AEPSO算法是收敛的。因为当 时,
时,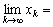
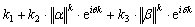 是发散的,其中θ和σ在每次迭代过程中是常量。
是发散的,其中θ和σ在每次迭代过程中是常量。
b. 当 ≥4c0,
≥4c0,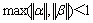 时,AEPSO可以保证算法收敛。在文献[14-15]中PSO算法控制参数常用选择方案的基础上,取c0≤0.729 8,
时,AEPSO可以保证算法收敛。在文献[14-15]中PSO算法控制参数常用选择方案的基础上,取c0≤0.729 8, ,
,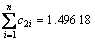 。由于
。由于
 ,
, ,因此,
,因此, ,
, 。当满足条件
。当满足条件 时,有r=
时,有r= ≥0,
≥0,
 ,AEPSO算法收敛;当
,AEPSO算法收敛;当
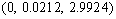 时,有
时,有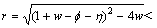
 ,
,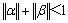 。因此,控制参数选择可以保证AEPSO算法的收敛性。
。因此,控制参数选择可以保证AEPSO算法的收敛性。
以上收敛性分析中没有考虑随机数r引发的概率性因素。由于 ,
, (其中r为(0, 1)间的随机数),因此,在粒子群的迭代过程中,控制参数
(其中r为(0, 1)间的随机数),因此,在粒子群的迭代过程中,控制参数 和
和 的期望值分别为:
的期望值分别为:
 ; (7)
; (7)
 。 (8)
。 (8)
因此,在考虑粒子群迭代过程中的概率随机因素的情况下,可以取 ,
,
 ,使得
,使得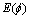
 (0,1.496 18),
(0,1.496 18), 
 (0,1.496 18),满足算法收敛。
(0,1.496 18),满足算法收敛。
综上所述,当控制参数取以下值时,AEPSO算法必收敛:

2 神经网络多步预测模型
2.1 系统描述
假设一个

这个模型通常是未知的,采用如下模型辨识:

2.2 递推多步预测模型
利用迭代算法可得

递推多步预测模型用一个神经网络就可完成系统的建模与多步预测,但由于系统模型不可避免地存在误差,因此,在递推过程中存在误差累积,这对于具有较大滞后的动态非线性系统更为明显。
2.3 直接多步预测模型
直接多步预测是通过构造多个不同的模型,完成系统的多步预测。

2.4 去误差直接多步预测模型
直接多步预测是通过构造多个不同的模型,完成系统的多步预测。由于神经网络的预测输出值和实际系统输出值之间不可避免地存在误差,且系统预测过程中存在一些不可预知的干扰影响,这里统一考虑为误差项[16]。以下分析误差项在直接多步预测模型中的影响。为了分析方便,利用NAR模型描述的系统分析其大范围预测器,所得结果可方便地推广到NARMAX系统。考虑NAR模型:

3 基于AEPSO优化的神经网络预测控制
3.1 基于AEPSO优化的神经网络预测控制算法
由于预测控制的任务在于使被控对象的输出y(k+j)尽可能地靠近设定值,故控制器设计的目标函数仍然使用二次性能指标:
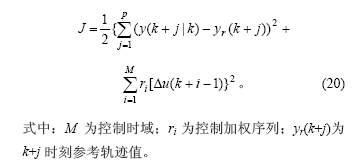

预测控制的目的在于在控制量的容许区间内寻求一组最优控制增量序列
 ,使得目标函数J最小,在每个采样周期内只以u(k)*投入控制,优化过程在线滚动进行。设控制时域为M,解空间维数为M,用AEPSO实现滚动优化的算法流程如下。
,使得目标函数J最小,在每个采样周期内只以u(k)*投入控制,优化过程在线滚动进行。设控制时域为M,解空间维数为M,用AEPSO实现滚动优化的算法流程如下。
步骤1:RBF(Radial Basis function)辨识网络NNI初始化,确定RBF网络结构,初始化网络权值及给定预测长度P等。
步骤2:离线训练NNI,辨识非线性系统。
步骤3:在 范围内,对M维空间随机地初始化一群微粒(群体规模型为d),包括随机位置与初始速度。
范围内,对M维空间随机地初始化一群微粒(群体规模型为d),包括随机位置与初始速度。
步骤4:将训练好的神经网络投入在线控制,保持网络权值不变,将不同粒子对应的u(k)值作为辨识模型输入,计算模型输出并在保持NNI权值不变的情况下进行递推,得到多步预测结果。
步骤5:根据式(20)和(21)计算每个微粒在当前情况下的适当度J。
步骤6:根据适应度值确定每个粒子m个个体极值和所有粒子n个局部极值。
步骤7:按式(1)~(3)变化微粒的方向与速度。
步骤8:迭代次数到,确定适应度最大的粒子,输出控制u(k)。
步骤9:在线修正NNI网络权值。
步骤10:返回步骤3,进入下一控制周期。
3.2 基于AEPSO优化的神经网络预测控制仿真
3.2.1 不同优化方法的预测控制对比

在仿真中,取RBF辨识网络输入层神经元个数取2,隐含层神经元数取6,输出层神经元数取1,学习速率η取0.3,动量因子α取0.5,采用递推多步预测模型。AEPSO的群体规模取30,最大代数取80,最优的个体极值粒子数目与局部最优粒子数目取
m=n=4,控制参数满足条件 ,
, ,且
,且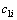 和
和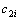 初始值均为
初始值均为
 。预测时域P=2,控制时域M=2,控制加权ri=0。采用基于AEPSO优化的神经网络预测控制方法跟踪周期为50的方波信号,柔化序列按下式建立:
。预测时域P=2,控制时域M=2,控制加权ri=0。采用基于AEPSO优化的神经网络预测控制方法跟踪周期为50的方波信号,柔化序列按下式建立:

控制方波跟踪仿真结果如图1所示,方波跟踪误差如图2所示。仿真结果表明,采用AEPSO优化的神经网络预测控制方法能够很好地跟踪设定值。
基于GA和PSO优化的神经网络预测方法[7, 10],其控制输出显示了较好的跟踪性能。表1给出了采用GA,PSO和AEPSO实现神经网络预测控制过程中滚动优化,跟踪周期为50的方波的误差均方差。采用RBF作为递推多步预测模型,网络结构与参数与以上相同,优化群体规模均为30,最大迭代步为80,预测时域取2,控制时域分别取1和2,GA优化算法的

图1 方波跟踪仿真结果
Fig.1 Simulation results for tracking square wave
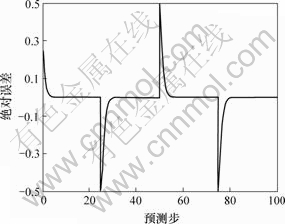
图2 方波跟踪误差
Fig.2 Errors for tracking square wave
表1 不同滚动优化方法跟踪误差均方差比较
Table 1 Comparison of mean square errors using different optimization methods

Pc=0.8,Pm=0.01;PSO优化算法的c0=1,c1=c2=0.5;AEPSO优化算法取值与以上相同。从表1可见,AEPSO与采用PSO和GA算法时相比,其跟踪误差均方差要小。
3.2.2 不同多步预测模型的对比
以AEPSO算法作为神经网络预测控制过程中的优化器,取预测时域为1时,控制时域为1,AEPSO参数与以上取值相同,柔化因子 取0.9。采用不同多步预测模型进行控制仿真,跟踪周期为50的方波信号的仿真结果如图3~5所示;控制时域取1,取不同预测时域跟踪周期为50的方波信号的均方差比较结果如表2所示。
取0.9。采用不同多步预测模型进行控制仿真,跟踪周期为50的方波信号的仿真结果如图3~5所示;控制时域取1,取不同预测时域跟踪周期为50的方波信号的均方差比较结果如表2所示。
从表2可见,当采用去误差直接多步预测模型时,基于AEPSO优化的神经网络预测控制系统具有较高的控制精度。
3.3 基于AEPSO优化的神经网络预测控制系统稳定性分析
基于AEPSO优化的神经网络预测控制系统的稳定性与AEPSO算法收敛性和RBF网络收敛性等价。
表2 不同预测方法跟踪误差均方差比较
Table 2 Mean square errors using different predictive methods

a. 径向基神经网络是全局收敛的。
b. AEPSO算法在满足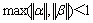 时是收 敛的。
时是收 敛的。
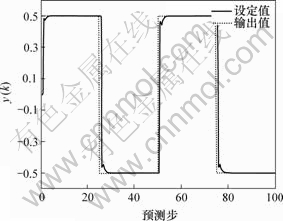
图3 去误差直接多步预测系统输出响应
Fig.3 Response of non-error directive multi-step prediction
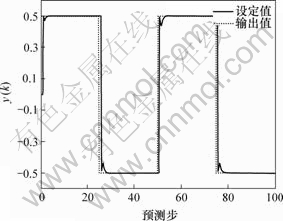
图4 直接多步预测系统输出响应
Fig.4 Response of directive multi-step prediction
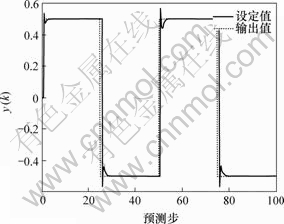
图5 递推多步预测系统输出响应
Fig.5 Response of recursive multi-step predictive
当AEPSO控制参数取上述初始值时,显然有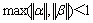 ,AEPSO优化算法收敛,因此,基于AEPSO优化的神经网络预测控制系统是稳定的。
,AEPSO优化算法收敛,因此,基于AEPSO优化的神经网络预测控制系统是稳定的。
4 结 论
a. 设计了一种新的自适应扩展粒子群优化算法,采用多粒子策略,提高算法的全局收敛性,同时,对控制参数c0进行自适应调整,提高算法的收敛速度。
b. 提出了基于自适应扩展粒子群优化的神经网络预测控制方案,运用AEPSO算法实现神经网络预测控制中的滚动优化,在有限时域内对控制序列进行寻列,给出了基于粒子群优化的神经网络预测控制系统的稳定性证明。仿真结果表明,基于自适应扩展粒子群优化的神经网络控制具有良好的跟踪性能,优于基于GA和PSO优化的预测控制。
参考文献:
[1] 诸 静. 智能预测控制及其应用于[M]. 杭州: 浙江大学出版社, 2002.
ZHU Jing. Intelligence predictive control and application[M].Hangzhou: Zhejiang University Press, 2002.
[2] 席裕庚. 预测控制[M]. 北京: 国防工业出版社, 1993.
XI Yu-geng. Predictive control[M]. Beijing: National Defense Technology Press, 1993.
[3] 杨煜普. 非线性系统多步预测控制的复合神经网络实现[J]. 控制与决策, 1999, 14(4): 314-318.
YNAG Yu-pu. Nonlinear multi-step predictive control using compound neural networks[J]. Control and Decision, 1999, 14(4): 314-318.
[4] 靳其兵, 王建辉. 多步预测性能指标函数下的神经网络逆动态控制方法[J]. 控制与决策, 1999, 14(4): 308-312.
JIN Qi-bing, WANG Jian-hui. Multi-step predictive cost function based reverse-dynamic method[J]. Control and Decision, 1999, 14(4): 308-312.
[5] Sorensen P H, Norgaard M. Implementation of neural network based nonlinear predictive control[J]. Neurocomputing, 1999, 28(1): 37-51.
[6] 杨 平, 彭道刚, 韩 璞. 神经网络预测控制算法及其应用[J]. 控制工程, 2003, 10(4): 349-353.
YANG Ping, PENG Dao-gang, HAN Pu. Neural network predictive control and application[J]. Control Engineering of China, 2003, 10(4): 349-353.
[7] Shin S C, Park S B. Ga-based predictive control for nonlinear processed[J]. Electronics Letter, 1998, 34(20): 1980-1981.
[8] 陈 华, 张小刚. 基于GA的神经网络预测控制仿真研究及应用[J]. 计算技术与自动化, 2003, 22(3): 19-23.
CHEN Hua, ZHANG Xiao-gang. Neural network predictive control simulation and application based on GA[J]. Computing Technology and Automation, 2003, 22(3): 19-23.
[9] 邹 健, 诸 静. 基于启发式遗传算法的非线性神经网络预测控制器[J]. 工业仪表与自动化装置, 2002, 32(1): 19-24.
ZOU Jian, ZHU Jin. A nonlinear neural network predictive controller based on heuristic genetic algorithm[J]. Industrial Instrumentation and Automation, 2002, 32(1): 19-24.
[10] XIAO Jian-mei. Research on neural network predictive control based particle swarm optimization[C]//Proceeding of the 5th World Congress on Intelligence Control and Automation. Hangzhou, 2004: 603-606.
[11] Shi Y, Eberhart R. Fuzzy adaptive particle swarm optimization[C]//Proceedings on Evolutionary Computation. Seoul, Korea, 2001: 152-168.
[12] 侯志祥, 申群太, 吴义虎. 基于Elman神经网络的汽油机过渡工况空燃比多步预测模型[J]. 中南大学学报: 自然科学版, 2006, 37(5): 981-985.
HOU Zhi-xiang, SHEN Qun-tai, WU Yi-hu. Multi-step predictive model of air fuel ratio of gasoline engine based on Elman neural network in transient condition[J]. Journal of Central South University: Science and Technology, 2006, 37(5): 981-985.
[13] Shi Y, Eberhart R. A modified particle swarm optimizer[C]//IEEE World Congress on Computational Intelligence. Washington, 1998: 207-219.
[14] LI Ling-lai. An effective hybrid PSOSA strategy for optimization and its application to parameter estimation[J]. Applied Mathematics and Compution, 2006, 179(1): 135-146.
[15] Fan S S. A hybrid simplex search and particle swarm optimization[J]. European Journal of Operational Research, 2007, 181(2): 527-548.
[16] WANG Xiao-chun. Self-tuning predictive control with forecasting factor for controe of pneumatic lumber handing system[J]. Internation Journal of Adaptive Control and Signal Processing, 2002, 14(5): 533-557.
收稿日期:2007-03-25;修回日期:2007-05-18
基金项目:国家自然科学基金资助项目(50276005);湖南省自然科学基金资助项目(05jj40087)
作者简介:侯志祥(1971-),男,湖南汉寿人,博士,副教授,从事智能控制研究
通信作者:侯志祥,博士,副教授;电话:0731-2309643;E-mail: houzhixiang2008@163.com