DOI: 10.11817/j.issn.1672-7207.2016.11.010
三级式无刷同步电机转子初始位置估算方法
毛帅,刘卫国,马鹏,彭纪昌
(西北工业大学 自动化学院,陕西 西安,710072)
摘要:提出一种三级式无刷同步电机在无位置传感器并且静止的情况下转子初始位置的估算方法。该方法首先利用三级式无刷同步电机主发电机定子铁心的饱和特性,通过给主发电机定子施加特定方向的电压空间矢量,检测并比较相应的定子电流来预估1个转子的初始位置。然后,利用预估的转子初始位置对主发电机定子电流进行造型,通过高斯曲线拟合估算转子初始位置。实验结果表明:转子初始位置的估算精度在0.5°电角度以内。
关键词:三级式无刷同步电机;无位置传感器;静止;转子初始位置;高斯曲线拟合
中图分类号:TM341 文献标志码:A 文章编号:1672-7207(2016)11-3685-07
Initial rotor position estimation of three-stage brushless synchronous motors
MAO Shuai, LIU Weiguo, MA Peng, PENG Jichang
(School of Automation, Northwestern Polytechnical University, Xi’an 710072, China)
Abstract: A method of estimating the initial rotor position of a three-stage brushless synchronous motor at standstill without any position sensors was presented. Based on the magnetic saturation characteristics of the stator core, the preliminary initial rotor position of the machine was estimated by applying specified voltage vectors to the main generator and comparing the stator current values. Then, the stator current values were modeled using the preliminary initial rotor position information and Gaussian curve fitting was performed. The results show that the standstill rotor position is within 0.5° in electrical angle.
key words: three-stage brushless synchronous motor; sensor-less; standstill; initial rotor position; Gaussian curve fitting
三级式无刷同步电机作为最常用的航空电机,其技术成熟[1]。随着飞机电源系统的发展,起动/发电双功能一体化的要求越来越迫切,以三级式无刷同步电机作为起动/发电机的研究具有重要意义[2]。在三级式无刷同步电机起动过程中,起动转矩是1个非常重要的参数[3]。在起动控制中,转子的初始位置直接影响到三级式无刷同步电机起动转矩。不准确的初始位置会引起电机带负载能力下降甚至反转等问题,导致起动失败,因此,三级式无刷同步电机的起动控制对转子的初始位置要求很高。位置传感器的安装会增加起动/发电系统的成本、体积和质量,其性能还会受到周围环境的影响,从而影响起动/发电系统可靠性[4],因此,在无位置传感器情况下得到转子的初始位置信息很有意义。由于三级式无刷同步电机起动过程中以航空发动机为负载,负载转矩很大且不允许反转,通过使电机转动进行转子初始位置估算的方法[5]不再适用,因此,三级式无刷同步电机起动控制系统需要在电机静止情况下得到转子的初始位置。曲线拟合是用连续曲线近似地刻画或比拟平面上离散点组函数关系的一种数据处理方法[6]。在工程实验中,通常可以获得若干离散的数据,从这些数据获取被测物理量之间某种近似的函数表达式具有非常重要的意义[7]。高斯函数适合描述数学和工程领域中的许多过程,应用广泛[8]。目前,同步电机转子初始位置估算方法有很多。金光哲等[9-10]针对电励磁同步电机提出在电机转子侧注入高频信号来检测转子初始位置的方法。该方法在同步电机的转子绕组中通入交流高频励磁电压,通过定子三相绕组的感应电压估算转子初始位置。通过锁相环跟踪技术,可以估算出转子的初始位置。但该方法需要测量反电势,增加了硬件要求;算法中要完成滤波器的设计,增加了系统的复杂性。由于三级式无刷同步电机主发电机的励磁电流是通过旋转整流器得到的,很难满足此方法对励磁的要求,所以,这种方法不适用于三级式无刷同步电机转子初始位置的估算。高频信号注入法是一种基于凸极追踪思想的转子初始位置估算方法。这种方法又可以分为2类:一是王高林等[11-12]提出的脉动高频电压信号注入法,二是于艳君等[13-14]提出的旋转高频电压信号注入法。这2类方法的基本原理[15]都是在电机中注入特定的高频电压(电流)信号,然后检测电机中对应的电流(电压)信号以确定转子的凸极位置。估算过程也需要设计滤波器,算法较复杂。利用电机定子铁心的饱和特性估算转子初始位置是最常用的一种方法[16-19]。这种方法原理简单,定位时间短,不需要电机参数,有一定的定位精度,是一种十分实用的方案,但这些研究基本上都是针对永磁同步电机来进行理论分析与实验验证的。三级式无刷同步电机结构中,主发电机的励磁电流是通过旋转整流器整流得到的。在主发电机励磁过程中,主发电机励磁电流波动较大,当励磁机采用单相交流励磁[20-22]时,主发电机转子励磁绕组的磁链没有永磁同步电机转子的永磁磁链稳定,所以,此方法应用于三级式无刷同步电机时,会有较大的估算误差。从理论上讲,此法的估算精度随着电压空间矢量细分程度的提高而提高。但实际使用时,由于存在检测元件误差、开关管死区时间等,使得仅仅通过电压空间矢量细分很难进一步提高估算精度,因此,不适合用于对转子初始位置要求较高的场合中。针对上述问题,本文作者提出一种三级式无刷同步电机在无位置传感器并且静止的情况下转子初始位置的估算方法。首先,利用三级式无刷同步电机主发电机定子铁心的饱和特性,通过给主发电机定子施加特定方向的电压空间矢量,检测并比较其相应的定子电流预估1个转子初始位置。然后,利用预估的转子初始位置对主发电机定子电流进行造型,消除采样数据的共模干扰,并通过高斯曲线拟合得到转子初始位置。
1 转子初始位置估算
1.1 估算原理
参考坐标系示意图如图1所示。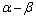 坐标系固定在主发电机的定子绕组上,d-q坐标系是同步旋转坐标系,d轴与转子的N极同向,qr表示转子的实际位置,
坐标系固定在主发电机的定子绕组上,d-q坐标系是同步旋转坐标系,d轴与转子的N极同向,qr表示转子的实际位置,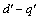 坐标系是估算坐标系。令
坐标系是估算坐标系。令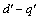 坐标系与静止坐标系A轴的夹角为q,
坐标系与静止坐标系A轴的夹角为q,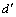 轴与施加在主发电机定子上的电压空间矢量Us同向,即
轴与施加在主发电机定子上的电压空间矢量Us同向,即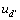 =Us,
=Us,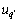 =0,
=0,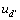 和
和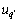 为
为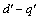 坐标系下的电压分量。
坐标系下的电压分量。
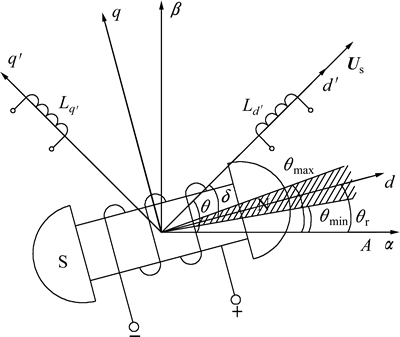
图1 参考坐标系示意图
Fig. 1 Diagram of reference frame
设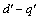 坐标系与转子轴线所在的d轴的夹角为d。随着
坐标系与转子轴线所在的d轴的夹角为d。随着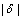 的减小,转子励磁磁通将与定子
的减小,转子励磁磁通将与定子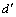 轴绕组交链越来越多,使得
轴绕组交链越来越多,使得 越来越小,当
越来越小,当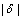 减小到0时,
减小到0时, 达到最小值
达到最小值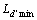 ,则其他位置的
,则其他位置的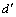 轴电感可表示为
轴电感可表示为
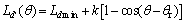 (1)
(1)
式中: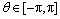 ;k>0,用于描述转子励磁磁通对
;k>0,用于描述转子励磁磁通对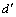 电感的影响。由永磁同步电机在任意两相同步旋转坐标系下的数学模型可知
电感的影响。由永磁同步电机在任意两相同步旋转坐标系下的数学模型可知
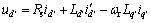 (2)
(2)
式中:Rs为定子电阻; 和
和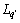 分别为
分别为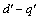 坐标系下的直轴和交轴电感;
坐标系下的直轴和交轴电感;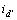 和
和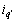 分别为
分别为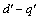 坐标系下的电流分量;
坐标系下的电流分量;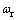 为电机的电角速度;
为电机的电角速度;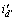 表示
表示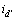 的导数。在估算过程中,电机静止,故
的导数。在估算过程中,电机静止,故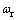 =0,忽略定子电阻压降,可得
=0,忽略定子电阻压降,可得
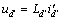 (3)
(3)
经过变形得
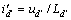 (4)
(4)
因此,当不同角度、相同幅值、相同作用时间的电压空间矢量作用后,在d′轴与d轴重合的位置电流id′最大,从而可以判断出转子N极的位置也就是转子的初始位置。
忽略阻尼绕组的影响,由三级式无刷同步电机主发电机在任意两相同步旋转坐标系下的数学模型可知
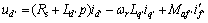 (5)
(5)
式中:励磁绕组对主发电机定子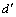 轴绕组的互感为Maf′;if′为主发电机转子的励磁电流。
轴绕组的互感为Maf′;if′为主发电机转子的励磁电流。
同理,ωr=0,忽略定子电阻压降,可得
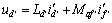 (6)
(6)
经变形得
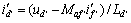 (7)
(7)
与式(4)相比,式(7)多了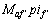 ,虽然在电流
,虽然在电流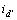 中,
中,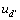 仍然起主导作用,但由于主发电机转子励磁电流的波动,并且在电流采样时刻,
仍然起主导作用,但由于主发电机转子励磁电流的波动,并且在电流采样时刻,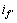 的变化是不确定的,所以,在
的变化是不确定的,所以,在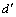 轴与d轴重合的这个位置,电流
轴与d轴重合的这个位置,电流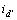 并不一定最大,存在如图1所示的阴影部分。在这部分区域内作用的电压空间矢量所得到的电流响应
并不一定最大,存在如图1所示的阴影部分。在这部分区域内作用的电压空间矢量所得到的电流响应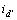 由于受到
由于受到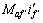 随机的干扰,最大的
随机的干扰,最大的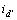 可能出现在阴影部分的任何1个位置,所以,若直接比较电流
可能出现在阴影部分的任何1个位置,所以,若直接比较电流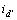 ,则会产生较大的估算误差。
,则会产生较大的估算误差。
由上述分析可知:电流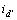 中包含了转子的初始位置信息。但在工程中,直接利用采集的电流
中包含了转子的初始位置信息。但在工程中,直接利用采集的电流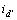 来进行分析会有较大的共模干扰,并且由本文实验结果可知电流
来进行分析会有较大的共模干扰,并且由本文实验结果可知电流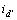 的分布特征不易找到1个较好的连续模型去拟合。因此,本文通过对电流
的分布特征不易找到1个较好的连续模型去拟合。因此,本文通过对电流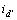 的采集结果进行造型,使其不但可以消除共模干扰,而且可以用常见的连续模型对观测结果进行拟合。
的采集结果进行造型,使其不但可以消除共模干扰,而且可以用常见的连续模型对观测结果进行拟合。
忽略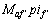 的干扰,令电压矢量的作用时间为ΔT,由式(4)可得
的干扰,令电压矢量的作用时间为ΔT,由式(4)可得
 (8)
(8)
对相差180°的2个电流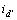 求差以消除共模干扰,得
求差以消除共模干扰,得
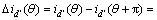
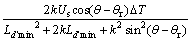 (9)
(9)
由对称性,取 。
。
通过Magnet软件对实验中的三级式无刷同步电机模型进行有限元仿真,得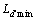 为k的2.85~6.25倍。以6.25倍(2.85倍与6.25倍的相似)为例,绘制
为k的2.85~6.25倍。以6.25倍(2.85倍与6.25倍的相似)为例,绘制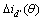 与
与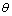 的关系,见图2。
的关系,见图2。
图2中, 对应的角度即转子的初始位置就是θr。考虑
对应的角度即转子的初始位置就是θr。考虑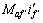 的影响时,在曲线的顶部附近会出现如图3所示的阴影区域,在此区域内,
的影响时,在曲线的顶部附近会出现如图3所示的阴影区域,在此区域内, 可能出现在阴影部分的任何1个位置,例如
可能出现在阴影部分的任何1个位置,例如 对应的角度可能是
对应的角度可能是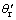 ,与真正的转子初始位置θr之间存在较大的误差。
,与真正的转子初始位置θr之间存在较大的误差。
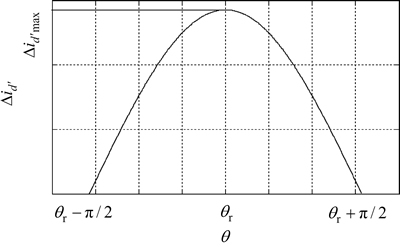
图2 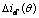 随q变化曲线(不考虑
随q变化曲线(不考虑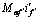 )
)
Fig. 2 Relationship between 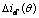 and θ regardless of
and θ regardless of 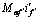
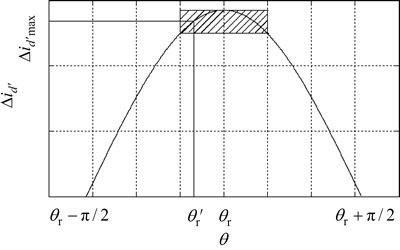
图3 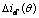 随q变化曲线(考虑
随q变化曲线(考虑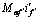 )
)
Fig. 3 Relationship between 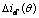 and θ regard of
and θ regard of 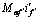
结合图2,可知图3在大部分范围内,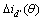 的分布特征与高斯函数相似,因此,选择高斯函数作为
的分布特征与高斯函数相似,因此,选择高斯函数作为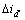 的连续模型。由于离散数据曲线拟合结果是对离散数据整体最好的逼近,因此,可以在很大程度上减小
的连续模型。由于离散数据曲线拟合结果是对离散数据整体最好的逼近,因此,可以在很大程度上减小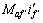 对转子初始位置估算的影响,通过拟合高斯函数曲线的顶点位置就可以确定θr,从而得到三级式无刷同步电机主发电机转子初始位置。
对转子初始位置估算的影响,通过拟合高斯函数曲线的顶点位置就可以确定θr,从而得到三级式无刷同步电机主发电机转子初始位置。
1.2 估算方法
按照上述原理,本文提出的估算方法分为2步。
1) 第1步:对转子初始位置进行预估。
首先通过励磁机对主发电机转子励磁,然后确定施加在主发电机定子上的电压空间矢量的幅值、作用时间以及相邻2个电压空间矢量间插入零矢量的时间,确保上述参数可以满足不损坏电机本体,并且每次施加电压空间矢量前,定子三相电流都已衰减到0 A,如图4所示。然后选择所施加的电压空间矢量个数n,如图5所示(以n=24为例,具体数值可以通过实验获得,当n大于某一值时,估算精度将不会有明显的变化)。
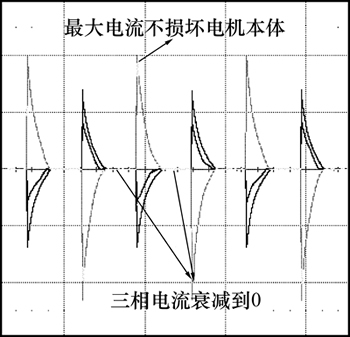
图4 电压空间矢量选择要求
Fig. 4 Requirements for voltage space vectors
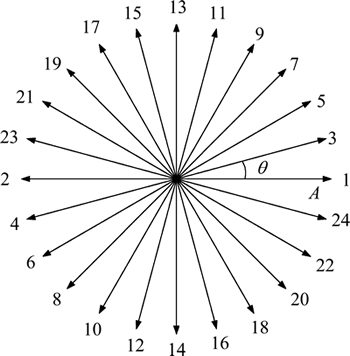
图5 电压空间矢量作用顺序
Fig. 5 Sequence of voltage space vectors
设每次作用的电压空间矢量与电机静止坐标系A轴的夹角为θ。为防止电机转动,按图5所示的顺序1~24向主发电机定子施加电压空间矢量,同时通过电流传感器采集定子三相电流。
取每次电压空间矢量作用完毕时对应的定子三相电流响应值iA,iB和iC,然后通过坐标变换得到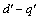 坐标系下的电流id′,坐标变换式为
坐标系下的电流id′,坐标变换式为
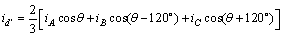 (10)
(10)
通过比较得出最大的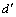 轴电流
轴电流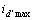 ,估算
,估算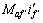 随机干扰引起
随机干扰引起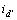 波动的最大值
波动的最大值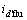 ,估算方法如下。
,估算方法如下。
将主发电机励磁电流波形进行放大可得图6,求取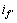 最大斜率的绝对值来得到
最大斜率的绝对值来得到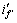 ,则
,则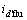 为
为
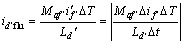 (11)
(11)
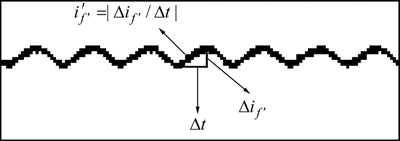
图6 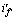 计算示意图
计算示意图
Fig. 6 Algorithm diagram of 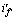
求出所有大于等于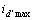 -
-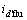 的
的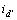 ,并找出对应的θ,比较得出其中的最大值θmax与最小值θmin。
,并找出对应的θ,比较得出其中的最大值θmax与最小值θmin。
当θmax-θmin<180°时,转子初始位置的预估值θr_temp由下式求得:
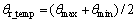 (12)
(12)
当θmax-θmin≥180°且360°-θmax≥θmin时,
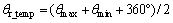 (13)
(13)
当θmax-θmin≥180°且360°-θmax<θmin时,
 (14)
(14)
2) 第2步:用高斯曲线拟合算法[23]得到转子的初始位置。
计算θtemp=θr_temp-90°。若θr_temp-90°<0°,则θtemp= θr_temp-90°+360°。令θk=360k/n(其中,n为电压空间矢量的个数,k为整数),对应的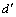 轴电流为
轴电流为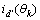 。当θk≥360°时,
。当θk≥360°时, ;当θk<0°时,
;当θk<0°时,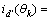
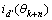 。求出使|θk-θtemp|最小的m,对应的
。求出使|θk-θtemp|最小的m,对应的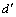 轴电流为
轴电流为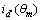 。令
。令
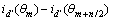 ,
,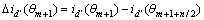 ,…,
,…,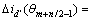
 。
。
对离散点(θm, ),(θm+1,
),(θm+1,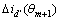 ),…,(θm+n/2-1,
),…,(θm+n/2-1, )进行高斯曲线拟合,拟合算法如下。
)进行高斯曲线拟合,拟合算法如下。
取高斯函数为
 (15)
(15)
其中:u,A和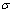 均为高斯函数中的待定系数。对式(15)两边取自然对数变形整理得
均为高斯函数中的待定系数。对式(15)两边取自然对数变形整理得
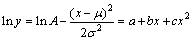 (16)
(16)
式中:
 (17)
(17)
定义误差
 (18)
(18)
定义矩阵
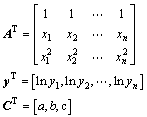 (19)
(19)
则线性拟合的法方程组 为
为
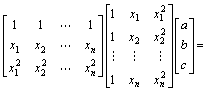
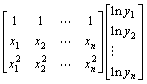 (20)
(20)
由式(20)得
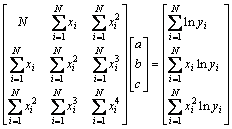 (21)
(21)
式中:N为采样数据的个数。由式(21)解得a,b和c。高斯函数的待定系数可由式(22)求解得到
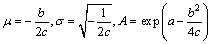 (22)
(22)
求出拟合系数μ,它为高斯函数最高点处的横坐标。由估算原理部分的分析可知:μ对应着转子N极的位置,即估算转子初始位置为θr=μ,若μ≥360°,则θr=μ-360°;若μ<0°,则θr=μ+360°。
2 实验结果与分析
2.1 实验条件
电压空间矢量的幅值Um=0.3(调制度),作用时间200 μs,相邻2个电压空间矢量间插入零矢量的时间为6 ms,选择所施加的电压空间矢量个数n=72(通过实验获得,当n大于72时,估算精度没有明显的变化,故选择n=72)。
本文的实验平台包括:1) 三级式无刷同步电机;2) MAGTROL公司的2PT115-T加载台;3) 以TMS320F2812为主控芯片的控制器;4) 直流电源、风机、示波器等辅助设备。
2.2 实验结果
电流响应值iA,iB和iC如图7所示。将iA,iB和iC变换到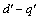 坐标系,得到电流
坐标系,得到电流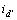 ,如图8所示,
,如图8所示,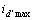 =255 A。从图8可以看出:此时离散数据
=255 A。从图8可以看出:此时离散数据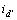 的分布特征不明显,不适合进行曲线拟合。估算得
的分布特征不明显,不适合进行曲线拟合。估算得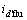 =6 A,找出所有大于等于
=6 A,找出所有大于等于 =249 A的
=249 A的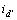 对应的角度,并求出其中的最大值θmax=95°与最小值θmin=75°。
对应的角度,并求出其中的最大值θmax=95°与最小值θmin=75°。
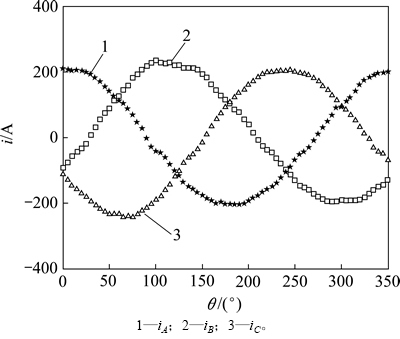
图7 不同电压空间矢量的电流响应曲线
Fig. 7 Curves of current response of different voltage space vectors
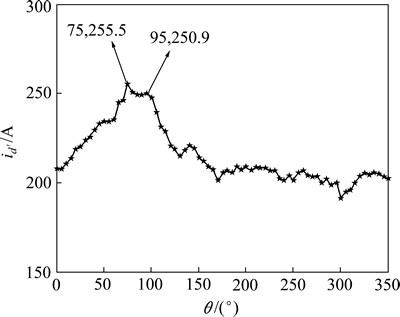
图8 d′轴电流曲线
Fig. 8 Curve of d′ axis current
初步估算转子初始位置值:θr_temp=(θmax+θmin)/2= 85°。计算θtemp=θr_temp-90°+360°=355°。求出使 |θk-θtemp|最小的m=71,对应的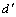 轴电流为
轴电流为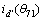 。令
。令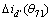 =
=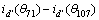 ,
,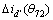 =
= 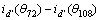 ,…,
,…,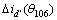 =
=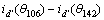 。
。
由(θ71,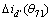 ),(θ72,
),(θ72,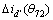 ),…,(θ106,
),…,(θ106,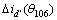 )描点作图,如图9所示。
)描点作图,如图9所示。
经过对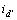 进行拟合,发现形状近似于高斯分布,与理论分析结果相符,因此,选用高斯函数对
进行拟合,发现形状近似于高斯分布,与理论分析结果相符,因此,选用高斯函数对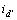 进行拟合。由本文提出的方法处理实验得到的三相电流可得μ=444.8,σ=35.1,A= 47.07,拟合结果如图9所示。因为μ≥360°,故θr=μ-360°=84.8°。所估算的转子初始位置84.8°与实际电机转子位置84.38°(由位置传感器测得)相差0.42°,完全满足三级式无刷同步电机起动控制的要求。
进行拟合。由本文提出的方法处理实验得到的三相电流可得μ=444.8,σ=35.1,A= 47.07,拟合结果如图9所示。因为μ≥360°,故θr=μ-360°=84.8°。所估算的转子初始位置84.8°与实际电机转子位置84.38°(由位置传感器测得)相差0.42°,完全满足三级式无刷同步电机起动控制的要求。
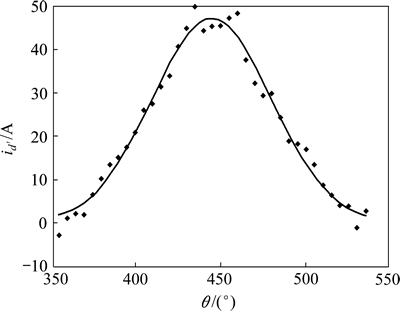
图9 高斯拟合曲线
Fig. 9 Curve of Gaussian fitting
3 结论
1) 提出了一种三级式无刷同步电机转子初始位置的估算方法,估算过程中转子保持静止,且不使用位置传感器。本方法分2步进行:首先利用三级式无刷同步电机主发电机定子铁心的饱和特性来预估1个转子的初始位置,然后通过高斯曲线对经过造型的离散数据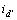 进行拟合估算出转子初始位置。
进行拟合估算出转子初始位置。
2) 转子初始位置的估算精度在0.5°电角度以内,完全满足三级式无刷同步电机起动控制的要求。本方法对电机参数不敏感,也可以用于隐极或凸极的永磁同步电机或电励磁同步电机中。
参考文献:
[1] LI Yanan, ZHOU Bo, WEI Jiadan, et al. Modeling of starter/generator based on three-stage brushless synchronous machines[C]//2010 International Conference on Electrical and Control Engineering. Wuhan, China, 2010: 5345-5348.
[2] 戴卫力, 王慧贞, 严仰光, 等. 航空起动/发电系统的发展趋势与研究现状[J]. 航空科学技术, 2010(5): 28-32.
DAI Weili, WANG Huizhen, YAN Yangguang, et al. Development trend and current situation of starter-generator for aircraft engine[J]. Aeronautical Science and Technology, 2010(5): 28-32.
[3] 焦宁飞, 刘卫国, 张华, 等. 一种变励磁无刷同步电机最大转矩电流比控制方法[J]. 微特电机, 2013, 41(1): 4-6.
JIAO Ningfei, LIU Weiguo, ZHANG Hua, et al. An MTPA control method for brushless synchronous machine with variational excitation[J]. Small & Special Electrical Machines, 2013, 41(1): 4-6.
[4] YAN Yang, GAO Hongwei. Initial rotor position estimation for low saliency interior permanent-magnet synchronous motor drives[C]//Applied Power Electronics Conference and Exposition (APEC). Texas, USA, 2011: 1022-1027.
[5] 朱熀秋, 成秋良. 无起动绕组永磁同步电机初始定位及起动策略[J]. 中国电机工程学报, 2008, 28(9): 61-65.
ZHU Huangqiu, CHENG Qiuliang. Initial orientation and starting strategy on PMSM without starting windings[J]. Proceedings of the CSEE, 2008, 28(9): 61-65.
[6] 乔立山, 王玉兰, 曾锦光. 实验数据处理中曲线拟合方法探讨[J]. 成都理工大学学报(自然科学版), 2004, 31(1): 91-95.
QIAO Lishan, WANG Yulan, ZENG Jinguang. Research of curve fitting methods in the experiment data processing[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2004, 31(1): 91-95.
[7] 唐冲, 惠辉辉. 基于Matlab的高斯曲线拟合求解[J]. 计算机与数字工程, 2013, 41(8): 1262-1263.
TANG Chong, HUI Huihui. Gaussian curve fitting solution based on Matlab[J]. Computer & Digital Engineering, 2013, 41(8): 1262-1263.
[8] GUO Hongwei. A simple algorithm for fitting a Gaussian function[J]. Signal Processing Magazine IEEE, 2011, 28(5): 134-137.
[9] 金光哲, 徐殿国, 高强, 等. 高频注入电压预估同步电机转子位置检测方法[J]. 中国电机工程学报, 2014, 34(9): 1376-1383.
JIN Guangzhe, XU Dianguo, GAO Qiang, et al. A synchronous motor rotor position detection method based on high-frequency injection voltage prediction[J]. Proceedings of the CSEE, 2014, 34(9): 1376-1383.
[10] 邓先明, 马志勋, 李新宇, 等. 转子注入高频的同步电机无传感器控制[J]. 电机与控制学报, 2010, 14(10): 61-67.
DENG Xianming, MA Zhixun, LI Xinyu, et al. Sensor-less control of synchronous motor based on high-frequency signal injection into the rotor[J]. Electric Machines and Control, 2010, 14(10): 61-67.
[11] 王高林, 杨荣峰, 李刚, 等. 基于高频信号注入的 IPMSM 无位置传感器控制策略[J]. 电工技术学报, 2012, 27(11): 62-68.
WANG Gaolin, YANG Rongfeng, LI Gang, et al. Position sensor-less control strategy of IPMSM based on high frequency signal injection[J]. Transactions of China Electrotechnical Society, 2012, 27(11): 62-68.
[12] 刘颖, 周波, 冯瑛, 等. 基于脉振高频电流注入SPMSM低速无位置传感器控制[J]. 电工技术学报, 2012, 27(7): 139-145.
LIU Ying, ZHOU Bo, FENG Ying, et al. Sensor-less control of SPMSM based on high frequency current signal injection in the direct axis at low and zero speed[J]. Transactions of China Electrotechnical Society, 2012, 27(7): 139-145.
[13] 于艳君, 柴凤, 欧景, 等. 基于旋转高频信号法的IPMSM无位置传感器控制[J]. 电工技术学报, 2013, 28(7): 26-31.
YU Yanjun, CHAI Feng, OU Jing, et al. Position sensor-less control of IPMSM based on rotating high frequency signal method[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 26-31.
[14] LORENZ R D.Practical issues and research opportunities when implementing zero speed sensor-less control[C]//Proceedings of the Fifth International Conference on Electrical Machines and Systems. Shenyang, China, 2001: 1-10.
[15] 秦峰, 贺益康, 刘毅, 等. 两种高频信号注入法的无传感器运行研究[J]. 中国电机工程学报, 2005, 25(5): 116-121.
QIN Feng, HE Yikang, LIU Yi, et al. Comparative investigation of sensor-less control with two high-frequency signal injection schemes[J]. Proceedings of the CSEE, 2005, 25(5): 116-121.
[16] NAKASHIMA S, INAGAKI Y, MIKI I. Sensor-less initial rotor position estimation of surface permanent-magnet synchronous motor[J]. IEEE Transactions on Industry Applications, 2000, 36(6): 1598-1603.
[17] 韦鲲, 金辛海. 表面式永磁同步电机初始转子位置估计技术[J]. 中国电机工程学报, 2007, 26(22): 104-109.
WEI Kun, JIN Xinhai. Initial rotor position estimate technique on surface mounted permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2007, 26(22): 104-109.
[18] BOUSSAK M. Implementation and experimental investigation of sensor-less speed control with initial rotor position estimation for interior permanent magnet synchronous motor drive[J]. IEEE Transactions on Power Electronics, 2005, 20(6): 1413-1422.
[19] TURSINI M, PETRELLA R, PARASILITI F. Initial rotor position estimation method for PM motors[J]. IEEE Transactions on Industry Applications, 2003, 39(6): 1630-1640.
[20] 陈宝林, 严仰光, 陈广华, 等. 飞机起动/发电双功能系统电动状态单相交流励磁的研究[J]. 电工技术杂志, 2001(1): 7-8.
CHEN Baolin, YAN Yangguang, CHEN Guanghua, et al. Study on single-phase AC excitation of electromotion state about start/generate electricity two function system of aeroplane[J]. Electric Engineering, 2001(1): 7-8.
[21] 顾毅康. 电磁式无刷交流同步电机新型起动方案研究[D]. 南京: 南京航空航天大学自动化学院, 2002: 21-41.
GU Yikang. Research on the new start scheme for brushless electro-magnetic synchronous AC motor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics. School of Automation, 2002: 21-41.
[22] 马鹏, 刘卫国, 骆光照, 等. 一种三级式航空无刷同步电机起动控制策略[J]. 电机与控制学报, 2012, 16(11): 29-32.
MA Peng, LIU Weiguo, LUO Guangzhao, et al. Starting control strategy for three-stage aviation brushless synchronous motor[J]. Electric Machines and Control, 2012, 16(11): 29-32.
[23] CARUANA R A, SEARLE R B, HELLER T, et al. Fast algorithm for the resolution of spectra[J]. Analytical Chemistry, 1986, 58(6): 1162-1167.
(编辑 陈灿华)
收稿日期:2015-10-11;修回日期:2015-12-06
基金项目(Foundation item):国家自然科学基金资助项目(51277152) (Project(51277152) supported by the National Natural Science Foundation of China)
通信作者:毛帅,博士研究生,从事同步电机伺服控制技术研究;E-mail: maoshuai1989@126.com