DOI： 10.11817/j.issn.1672-7207.2020.07.026

车轮谐波磨耗对轮轨垂向力及车辆稳定性的影响

谢建平^{1, 2},陈治亚¹,潘瑛²,谢建波²,王乾宇²

（1. 中南大学 交通运输工程学院，湖南 长沙，410075；

2. 长沙市轨道交通集团有限公司，湖南 长沙，410133）

摘要:基于车辆车轮在生产过程中存在质量偏心或几何偏心，导致列车在运行一段时间之后出现车轮谐波磨耗现象，车轮谐波磨耗将对轮轨垂向力及车辆稳定性产生严重影响，以国内某地铁车辆为参考，运用车辆轨道耦合模型理论，采用Fourier级数模拟2阶、3阶车轮谐波磨耗，建立该车的车辆/轨道耦合模型及车轮谐波磨耗模型。仿真计算车轮谐波磨耗及轨道不平顺激扰等因素对轮轨垂向力及车辆稳定性的影响，并分析车辆在单一激扰工况和叠加激扰工况下车辆动力学参数的差异。研究结果表明：速度对轮轨垂向力的影响远大于幅值和相位差对轮轨垂向力的影响，轨道不平顺激扰对轮轨垂向力的影响不大；随着速度增大，车轮谐波磨耗对车辆运行平稳性影响越显著。

关键词:车轮谐波磨耗；车辆/轨道耦合模型；单一激扰；叠加激扰；轮轨垂向力；车辆稳定性

中图分类号:U260.11      文献标志码:A       开放科学(资源服务)标识码(OSID)

文章编号:1672-7207（2020）07-2013-08

Influence of wheel harmonic wear on wheel-rail vertical force and vehicle stability

XIE　Jianping^{1, 2}, CHEN　Zhiya¹, PAN　Ying², XIE　Jianbo², WANG　Qianyu²

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China；

2. Changsha Metro Group Co. Ltd., Changsha 410133, China)

Abstract: Considering that in the production process of vehicle wheels,there are mass eccentricity or geometric eccentricity, the harmonic wear of wheels occurs after the train runs for a period, wheel harmonic wear seriously affects wheel-rail vertical force and vehicle stability, a subway vehicle in China was taken as a reference, the theory of vehicle-track coupling model and Fourier series were used to simulate the 2nd and 3rd order wheel harmonic wear,and the vehicle-track coupling model and wheel harmonic wear model of the vehicle were established.The effects of wheel harmonic wear and track irregularity excitation on wheel-rail vertical force and vehicle stability were simulated and calculated. The difference of vehicle dynamic parameters between single excitation and superposition excitation conditions was analyzed.The results show that the influence of velocity on wheel-rail vertical force is much greater than that of the amplitude and phase difference.Track irregularity excitation has little effect on wheel-rail vertical force. With the increase of speed, the wheel harmonic wear irregularity excitation has significant impact on vehicle running smoothness.

Key words: wheel harmonic wear; vehicle/track coupling model; single excitation; superposition excitation; wheel-rail vertical force; vehicle stability

地铁列车运行时产生的振动不仅会对车辆部件和轨道线路产生严重损坏，而且将严重影响旅客乘坐的舒适程度。对列车在运行中的振动特性进行研究，首先需要对引起列车振动的激振源进行研究。列车振动主要是由车轮非圆化和轨道不平顺2部分引发。在列车车轮非圆化的所有问题中，车轮谐波磨耗是车轮非圆化问题中最常见的形式之一^[1]，车轮谐波磨耗也常称为车轮多边形、车轮周期性非圆化和车轮波磨^[2]。针对地铁列车车轮谐波磨耗对轮轨垂向力及车辆稳定性的影响，国内外许多学者进行了研究，如：JOHANSSON等^[3-5]采用试验与仿真相结合的方法分析了车轮谐波磨耗对轮轨垂向力的影响；LIU等^[6]针对高速列车车轮谐波磨耗对轮轨垂向力及轮轨相互作用的影响进行了研究；吴磊等^[7]研究了多种工况下车轮谐波磨耗对轮轨法向力和脱轨系数的影响，分析了其对列车安全性能的影响；王忆佳等^[8]通过改变车轮谐波磨耗的幅值研究分析了不同车速下阶车轮多边形幅值的安全限值；WU等^[9]通过研究发现车轮谐波磨耗激振频率对轮轴动应力有极大影响；张雪珊等^[10-12]建立了一种新的2阶车轮谐波磨耗的数学模型，仿真分析了高速状态下2阶车轮谐波磨耗对车辆横向稳定性的影响；罗仁等^[13]综合考虑相关部件的非线性特征，对车轮谐波磨耗的演变机理及其对动力学性能的影响进行了研究；刘韦等^[14-17]将轮对视为弹性体建立车辆/轨道耦合模型，研究了4种模型下车轮多边形对轮轨系统振动响应的影响。对相邻轮对输入不同阶次车轮谐波磨耗，且与轨道激扰叠加引起轮轨垂向力及车辆稳定性发生变化，而目前人们对此研究很少，为此，本文作者基于车辆/轨道耦合动力学理论，使用SIMPACK软件建立列车的车辆/轨道耦合模型，计算分析单一激扰工况和叠加激扰工况对轮轨垂向力及车辆稳定性的影响，以便为进一步研究车轮谐波磨耗对车辆动力学的影响提供参考。

1 数值模型

1.1　车轮谐波磨耗模型

车轮谐波磨耗即车轮半径沿整个圆周呈周期性变化，本文建立2阶和3阶车轮谐波磨耗的物理模型，如图1所示。车轮在非圆化形成过程中，轮对左右两端的车轮总是会或多或少存在一定程度的相位差，图1(a)和图1(b)中的实线和虚线分别表示2阶和3阶车轮谐波磨耗轮对左右两端的车轮相位相差90°的示意图。

图1　车轮谐波磨耗示意图

Fig. 1　Schematic diagram of wheel harmonic wear

国际上，车轮谐波磨耗多采用含有阶谐波的Fourier级数形式的唯一函数来描述^[18]，即

(1)

式中：为第阶车轮谐波磨耗的幅值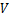；为列车运行速度；为车轮谐波磨耗的半径；为第阶车轮谐波磨耗的相位；t为时间。在车轮谐波磨耗激扰下，对轮轨系统动态行为起关键作用的因素包括列车速度、车轮谐波磨耗的幅值及轮对左右两端车轮存在的相位差。本文对单一激扰工况和叠加激扰工况作用下列车速度、车轮谐波磨耗的幅值及轮对左右两端车轮存在的相位差对轮轨垂向力及车辆稳定性的影响进行分析。单一激扰工况及叠加激扰工况示意图如图2所示，两者的区别在于是否在轨道中加入激扰，模型中加入激扰的轨道谱为美国Ⅴ级轨道谱。美国Ⅴ级轨道谱使用以下3个公式进行描述^[19]。

1) 对于轨道高低不平顺，

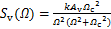(2)

2) 对于轨道方向不平顺，

(3)

3) 对于轨道水平及轨距不平顺，

(4)

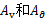式中：为轨道不平顺功率谱密度；为轨道不平顺的空间频率；为粗糙度常数，美国Ⅴ级轨道谱中取0.209 5，取0.076 2；和为截断频率，美国Ⅴ级轨道谱中取0.824 5，取0.820 9；为安全系数，可根据要求在之间选取，一般取0.25。

图2　单一激扰工况及叠加激扰工况示意图

Fig. 2　Schematic diagrams of single and superimposed excitation conditions

1.2　车辆轨道耦合模型

为了研究单一激扰工况和叠加激扰工况对轮轨垂向力及车辆稳定性的影响，使用动力学软件SIMPACK建立某地铁动车车辆/轨道耦合动力学模型^[19]，如图3所示，其最高运行速度为120 km/h。该动车可以简化为由1个车体、2个构架、2个横向液压减振器、4个横向止档、8个垂向止档、8个一系垂向液压减振器等组成的50自由度多刚体动力学系统。为更加真实反映定员工况下车辆的动力学性能，模型中充分考虑了相关部件非线性特性。

图3　车辆/轨道耦合模型图

Fig. 3　Vehicle/track coupling model

2 车轮谐波磨耗对轮轨垂向力的影响

对车辆/轨道耦合模型按照图2所示输入激励，研究速度、幅值、相位差及轨道激扰对轮轨垂向力的影响，结果如图4所示。由图4可知：当幅值从0.1 mm逐渐增大到0.9 mm时，轮轨垂向力大致呈线性增大。从图4(a)可见：当列车速度为100 km/h，幅值为0.9 mm时，轮轨垂向力达到最大值和最小值，其中，最大值为90.977 5 kN，最小值为38.943 6 kN，此时，轮轨垂向力波动最剧烈。出现该现象的原因主要是在该工况下，轮轨的冲击频率与轮对自身的弯曲模态频率接近，导致在该工况下系统出现共振。对比图4(a)和图4(b)可知：当列车速度为100 km/h，相位差为45°时，轨道不平顺激扰的加入使轮轨垂向力不再随幅值增加而呈线性增大；当速度低于80 km/h，幅值低于0.7 mm时，轨道激扰的加入将使轮轨垂向力小幅度增加；当列车速度为100 km/h，幅值为0.9 mm时，轮轨垂向力不再达到最大值和最小值。由此可知：轨道激扰的加入改变了轮轨的冲击频率，避免了该工况下共振的产生。

考虑车轮谐波磨耗幅值为0.7 mm，将轮对相位差从30°逐渐增加到90°时，分析列车在40～120 km/h速度范围内轮轨垂向力的变化情况，结果如图5所示。由图5(a)可知：在中、低速时，随着轮对相位差增大，轮轨垂向力变化不大；当列车速度增大到80 km/h以上时，轮轨垂向力快速增大；当相位差从60°增加到90°时，轮轨垂向力急剧增大，可知相位差只有在高速时才会对轮轨垂向力产生显著影响。由图5(b)可见：当轨道存在缺陷时，轮对激扰易与轨道激扰发生耦合，轮轨耦合促使系统的垂向轮轨力趋向于发生不规则变化。

图4　速度及幅值对轮轨垂向力的影响

Fig. 4　Effect of velocity and amplitude on wheel-rail vertical force

图5　速度及相位差对轮轨垂向力的影响

Fig. 5　Effect of velocity and phase difference on wheel-rail vertical force

综合分析图4和图5可知：在中、低速时，不管是速度、幅值、相位差还是轨道不平顺均对轮轨垂向力无显著影响，可知空气弹簧及二系垂向液压减振器对中、低频的垂向振动有很好的抑制作用；在单一激扰工况时，轮轨垂向力最大值均随着速度的增加而增加，轮轨垂向力最小值则随之增大而减小。对比图4(a)和图5(a)可知：相位差对轮轨垂向力的影响较幅值对轮轨垂向力的影响更明显，但相位差与幅值对轮轨垂向力的影响均不如速度对轮轨垂向力的影响显著。通过对影响轮轨垂向力的各因素进行分析计算，发现对轮轨垂向力的影响程度由大至小分别为速度、相位差、幅值。

3 车轮谐波磨耗对车辆平稳性的影响

车辆运行平稳性指标W_i采用Sperling指标^[19]，计算式为

(5)

式中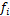：为第i频段振动频率(Hz)；为第i频段频率修正系数。频率修正系数如表1所示。

表1　机车车辆平稳性指标计算公式的频率修正系数

Table 1　Frequency correction coefficient of calculation formula of locomotive and vehicle stability index

由于车辆的振动是随机振动，其加速度和频率随时都在变化，对加速度和频率进行实际评定时，将所要分析的加速度波形按频率分组，根据每一组的加速度和频率计算该组的平稳性指标。整个波形的平稳性指标按下式计算：

(6)

式中：N为整个波段的分组总数。GB 5599—85中关于机车车辆的平稳性等级如表2所示，其中垂向和横向平稳性采用相同的评定等级。

图6　速度及幅值对车体垂向平稳性的影响

Fig. 6　Effect of velocity and amplitude on vertical stability of car body

表2　我国机车车辆平稳性评定等级

Table 2　Evaluation standard of vehicle stability

3.1　车轮谐波磨耗对车体垂向平稳性的影响

车体垂向平稳性指标随速度、幅值及相位差的变化规律曲线见图6和图7。从图6和图7可知速度、幅值及相位差对车体垂向平稳性指标影响的变化规律与图4和图5所示的类似。由图6(a)可知：在相位差为45°，幅值为0.3 mm，列车速度从40 km/h增大到60 km/h时，车体垂向平稳性指标增大16%；当列车速度从100 km/h增大到120 km/h时，车体垂向平稳性指标增大22%。这说明速度越大，车体垂向平稳性的增长率也越大。从图6可知：当相位差为45°，在同一速度等级下，幅值从0.1 mm增大到0.7 mm时，车体垂向平稳性指标缓慢增加；当幅值从0.7 mm增大到0.9 mm时，车体垂向平稳性指标急剧增加。由图6(b)可知：当幅值为0.9 mm，速度从100 km/h增加到120 km/h时，车体垂向平稳性指标达到2.721，达到GB 5599—85的2级标准。由此可知车轮谐波磨耗幅值越大，对车辆垂向平稳性的影响也越大。

图7所示为车体垂向平稳性指标随速度及相位差变化的点线图。对比图7(a)和图7(b)可知：随着轨道激扰加入，在速度为120 km/h、相位差为90°时，车体垂向平稳性指标出现急剧增大趋势。可知轨道不平顺激扰与90°相位差相互耦合所产生的振动已接近系统减振装置的极限值，最终导致系统在该工况时，车体垂向平稳性指标急剧增大。对图6和图7进行综合分析可知：当速度在100 km/h以内时，车辆垂向平稳性指标均小于2.5，达到GB 5599—85的1级标准；在叠加激扰工况下，当速度从100 km/h增加到120 km/h时，车体垂向平稳性指标将大于2.50且小于2.75，达到GB 5599—85的2级标准^[20]。

图7　速度及相位差对车体垂向平稳性的影响

Fig. 7　Effect of velocity and phase difference on vertical stability of car body

3.2　车轮谐波磨耗对车体横向平稳性的影响

当列车在轨道上行驶时，对列车速度、幅值及相位差对车体横向平稳性的影响进行仿真研究，结果图8和图9所示。由图8和图9可知：在单一激扰工况和叠加激扰工况下，车体横向平稳性指标均小于2.5，达到GB 5599—85的1级标准。

图8　速度及幅值对车体横向平稳性的影响

Fig. 8　Effect of velocity and amplitude on lateral stability of car body

图9　速度及相位差对车体横向平稳性的影响

Fig. 9　Effect of velocity and phase difference on lateral stability of car body

从图8可知：在单一激扰工况、相位差一定的条件下，车体横向平稳性指标随着列车速度及幅值增加而增加；叠加激扰工况时，车体横向平稳性指标相对于单一激扰工况也只存在极小幅度提升；当列车在美国Ⅴ级轨道谱上行驶时，轨道不平顺会对特定速度及幅值下的车体横向平稳性有一定的增强或衰减作用。虽然从图8(b)中看不出明显的规律，但可以确定造成这种现象的原因是轨道不平顺和车轮谐波磨耗相互耦合所致。

速度及相位差对车体横向平稳性指标的影响见图9。从图8(a)和图9(b)可知：当幅值为0.7 mm、相位差为45°时，车辆横向平稳性指标呈现跳跃式增大，但车体横向平稳性指标仍然小于2.5。这是因为在45°相位差下，由1个转向架上相邻2阶和3阶谐波磨耗产生的横向冲击频率与转向架的3阶弯曲模态频率、轴箱摇头运动频率相近，从而使系统出现共振现象；当相位差由45°增大至90°时，车体横向平稳性指标反而急剧减小。由此可知：当系统未发生共振时，轴箱定位装置及横向减振器对由轮对相位差所引起的横向振动有很强的衰减作用。在图9(b)中，轨道激扰的加入使相位差为45°时的共振频率发生转移，车体横向平稳性指标降低。虽然相位差为75°和90°工况下车体横向平稳性指标有所增加，但其在120 km/h的速度下曲线都趋向于平缓，证明其受到了系统减振装置的作用。

4 结论

1) 轨道激扰的加入对轮轨垂向力和车辆平稳性均产生不同程度的不利影响。同时，考虑轮对激扰和轨道激扰能更加真实地反映轮轨关系对车辆动力学参数的影响。

2) 在中、低速时，不管是速度、幅值、相位差还是轨道不平顺均对轮轨垂向力无显著影响。这4种影响因素对轮轨垂向力的影响程度由高至低依次为速度、相位差、幅值和轨道不平顺。

3) 车轮谐波磨耗幅值对车辆垂向平稳性有较大影响，对车辆横向平稳性影响较小，且车轮谐波磨耗幅值越大，对车辆垂向平稳性的影响也越大。

4) 相位差对车体垂向平稳性的影响远大于对车体横向平稳性的影响，在叠加激扰工况下、列车速度从100 km/h增加到120 km/h时，车体垂向平稳性指标将大于2.50且小于2.75，达到GB 5599—85的2级标准。

参考文献：

[1] 周新建, 肖乾, 程树, 等. 柔性轨道下高速列车车轮谐波磨耗对轮轨滚动接触蠕滑特性的影响[J]. 中国铁道科学, 2017, 38(4): 84-91.

ZHOU Xinjian, XIAO Qian, CHENG Shu, et al. Influence of wheel harmonic wear of high speed train on creep characteristics of wheel-rail rolling contact under flexible track[J]. China Railway Science, 2017, 38(4): 84-91.

[2] JIN Xuesong. Key problems faced in high-speed train operation[J]. Journal of Zhejiang University: Science A, 2014, 15(12): 936-945.

[3] JOHANSSON A, NIELSEN JCO. Out-of-round railway wheels: wheel-rail contact forces and track response derived from field tests and numerical simulations[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2003, 217(2): 135-146.

[4] BARKE D W, CHIU W K.A review of the effects of out-of-round wheels on track and vehicle components[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2005, 219(3): 151-175.

[5] NIELSEN J C O, JOHANSSON A.Out-of-round railway wheels-a literature survey[J]. Proceedings of the Institution of Mechanical Engineers,Part F: Journal of Rail and Rapid Transit, 2000, 214(2): 79-91.

[6] LIU Xiaoyuan, ZHAI Wanming. Analysis of vertical dynamic wheel/rail interaction caused by polygonal wheels on high-speed trains[J]. Wear, 2014, 314(1/2): 282-290.

[7] 吴磊, 钟硕乔, 金学松, 等. 车轮多边形化对车辆运行安全性能的影响[J]. 交通运输工程学报, 2011, 11(3): 47-54.

WU Lei, ZHONG Shuoqiao, JIN Xuesong, et al. Influence of polygonal wheel on running safety of vehicle[J]. Journal of Traffic and Transportation Engineering, 2011, 11(3): 47-54.

[8] 王忆佳, 曾京, 罗仁, 等. 高速列车车轮多边形化对车辆动力学性能的影响[J]. 四川大学学报(工程科学版), 2013, 45(3): 176-182.

WANG Yijia, ZENG Jing, LUO Ren, et al. Effect of polygonal wheel on vehicle dynamic performance[J]. Journal of Sichuan University(Engineering Science Edition), 2013, 45(3): 176-182.

[9] WU Xingwen, CHI Maoru, WU Pingbo. Influence of polygonal wear of railway wheels on the wheel set axle stress[J]. Vehicle System Dynamics, 2015, 53(11): 1535-1554.

[10] 张雪珊, 肖新标, 金学松. 高速车轮椭圆化对车辆系统行为的影响[J]. 机械工程学报, 2010, 46(16): 67-73.

ZHANG Xueshan, XIAO Xinbiao, JIN Xuesong. Effect of ovalization of high speed railway wheels on vehicle dynamic performance[J]. Journal of Mechanical Engineering, 2010, 46(16): 67-73.

[11] 张雪珊, 肖新标, 金学松. 高速车轮椭圆化问题及其对车辆横向稳定性的影响[J]. 机械工程学报, 2008, 44(3): 50-56.

ZHANG Xueshan, XIAO Xinbiao, JIN Xuesong. Influence of high speed railway wheels ovalization on vehicle lateral stability[J]. Journal of Mechanical Engineering, 2008, 44(3): 50-56.

[12] 张雪珊, 张剑, 张军. 高速车轮椭圆化模型研究[J]. 科学技术与工程, 2010, 10(8): 1902-1906, 1918.

ZHANG Xueshan, ZHANG Jian, ZHANG Jun. Study on model of high speed railway wheel ovalization[J]. Science Technology and Engineering, 2010, 10(8): 1902-1906, 1918.

[13] 罗仁, 曾京, 邬平波, 等. 高速列车车轮不圆顺磨耗仿真及分析[J]. 铁道学报, 2010, 32(5): 30-35.

LUO Ren, ZENG Jing, WU Pingbo, et al. Simulation and analysis of wheel out-of-roundness wear of high-speed train[J]. Journal of the China Railway Society, 2010, 32(5): 30-35.

[14] 刘韦, 马卫华, 罗世辉, 等. 考虑轮对弹性的车轮振动及车轮多边形化对轮轨力影响研究[J]. 铁道学报, 2013, 35(6): 28-34.

LIU Wei, MA Weihua, LUO Shihui, et al. Research on influence of wheel vibration and wheel polygonization on wheel-rail force in consideration of wheelset elasticity[J]. Journal of the China Railway Society, 2013, 35(6): 28-34.

[15] 宋志坤, 岳仁法, 胡晓依, 等. 车轮多边形对车辆振动及轮轨力的影响[J]. 北京交通大学学报, 2017, 41(6): 88-93.

SONG Zhikun, YUE Renfa, HU Xiaoyi, et al. Influence of wheel polygon on vehicle vibration and wheel/rail force[J]. Journal of Beijing Jiaotong University, 2017, 41(6): 88-93.

[16] 胡晓依, 侯银庆, 宋志坤, 等. 基于柔性轮轨模型的车轮谐波磨耗对高速轮轨系统振动影响的仿真研究[J]. 中国铁道科学, 2018, 39(6): 81-89.

HU Xiaoyi, HOU Yinqing, SONG Zhikun, et al. Simulation study on influence of harmonic wear of wheel on vibration of high-speed wheel-rail system based on flexible wheel-rail model[J]. China Railway Science, 2018, 39(6): 81-89.

[17] 宋志坤, 侯银庆, 胡晓依, 等. 柔性轮轨下轮轨波磨综合作用的振动特性研究[J]. 铁道学报, 2018, 40(11): 33-40.

SONG Zhikun, HOU Yinqing, HU Xiaoyi, et al. Research on vibration characteristics of wheel-rail corrugation under flexible wheel and rail[J]. Journal of the China Railway Society, 2018, 40(11): 33-40.

[18] 吴越, 韩健, 刘佳, 等. 高速列车车轮多边形磨耗对轮轨力和转向架振动行为的影响[J]. 机械工程学报, 2018, 54(4): 37-46.

WU Yue, HAN Jian, LIU Jia, et al. Effect of high-speed train polygonal wheels on wheel/rail contact force and bogie vibration[J].J ournal of Mechanical Engineering, 2018, 54(4): 37-46.

[19] 翟婉明. 车辆-轨道耦合动力学[M]. 北京: 科学出版社, 2007: 44-48.

ZHAI Wanming. Vehicle-railway coupling dynamics[M]. Beijing: China Science Publish House, 2007: 44-48.

[20] 邢璐璐. 弹性车轮车辆动力学研究[D]. 成都: 西南交通大学机械工程学院, 2012: 53-55.

XING Lulu. Study on resilient wheel vehicle dynamics[D]. Chengdu: Southwest Jiaotong University. College of Mechanical Engineering, 2012: 53-55.

（编辑 陈灿华）

收稿日期： 2019 -09 -12; 修回日期： 2019 -11 -21

基金项目(Foundation item)：湖南省科技重大专项(2015GK1006) (Project(2015GK1006) supported by the Major Science and Technology Program of Hunan Province)

通信作者：谢建平，高级工程师，从事轨道交通运输管理研究；E-mail：744833658@qq.com