DOI: 10.11817/j.issn.1672-7207.2015.11.052
铁路线路建设时序决策模型与应用
冯芬玲，姬志洲，汤子文，陈治亚
(中南大学 交通运输工程学院，湖南 长沙，410075)
摘要：为科学、合理地安排铁路线路建设，提高铁路建设资金的使用效率，考虑新建线路的碳排放、投资回报率和对铁路网的作用，采用主观赋权的层次分析法和客观赋权的熵值法，引入主观系数，确定各决策指标的权重，建立铁路线路建设时序决策模型；考虑铁路建设对国民经济的重大影响，铁路线路建设时序应该符合国家经济政策发展趋势以及地方的需求，提出政策系数，改进铁路线路建设时序决策模型。实例分析结果验证改进后决策模型的正确性。
关键词：线路建设；建设时序；投资回报率；碳排放
中图分类号：U211 文献标志码：A 文章编号：1672-7207(2015)11-4370-07
Construction schedule model and applications on railway line
FENG Fenling, JI Zhizhou, TANG Ziwen, CHEN Zhiya
(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)
Abstract: In order to conduct the railway line construction scientifically and reasonably, and improve the efficiency of railway line construction fund, carbon emissions and the effect on the rail network of newly-built lines were referred, the analytic hierarchy process (AHP) of subjective empower and the entropy value method of objective empower were used, the subjective factor and the weight of each index were introduced, and the railway line construction schedule model was established. Considering the significant effect of the railway construction on the national economy, and that railway line construction schedule should conform to the development trend of national economic policies and local requirements, the policy factors to improve the railway line construction schedule model were established. The case analysis results verify the model’s correctness.
Key words: line construction; construction schedule; return on investment; carbon emissions
铁路运输是中国综合运输体系中的重要组成部分。铁路建设是一项长期、庞大的系统性工程，需耗费大量人力、物力和财力，只有当各种条件满足一定要求时才能被批准建设。铁路投资回收周期长，在资源、经济能力有限的条件下，还不能满足所有铁路的建设，审批部门要从长远角度，严格控制铁路线路建设的时序及总量，确保铁路建设符合国家长远经济发展的需要。目前，国内外对铁路线路建设时序问题研究较少。冯林祥等[1]对铁路建设项目投资时序进行了探讨，提出投资时滞概念。何学刚[2]分析了四川省各个方向铁路输送能力与需求，并根据运能与需求的情况确定四川在建、拟建对外铁路通道的建设时序。钟新等[3]结合区域路网概况，针对福厦铁路运量预测情况，分析其建设规模，并研究不同建设模式下福厦(福州—厦门)通道建设的适应性。在城市轨道交通建设领域，Song等[4]在研究武汉城市轨道交通的建设时序时，通过不同阶段客流预测模型，获取各线路流量分配，考虑融资能力以及综合实力，重点从客票收入和效益方面研究线路建设时序问题；吴其刚等[5]从运输需求、运输供给、融资政策、可替代性以及效益等方面研究城市轨道交通的准入条件，建立了城际铁路建设时序决策模型；郭延永等[6-7]运用TOPSIS模型和累计前景理论，研究城市轨道交通建设时序确定方法；Luo等[8]运用模糊数学理论，提出了基于加权灰色关联度的城市轨道交通建设时序方法。在其他相关领域，Greg 等[9]讨论了基于线性调度程序的工程进度管理；Tang等[10]使用线性调度与约束编程相结合来解决铁路建设过程中面临的进度控制问题，包括进度控制模型、调度模型和调度控制模型，提高线性工程建设的时间和空间的管理效率；王振报等[11]定义了客运枢纽建设时序的指标，利用动态优化流程确定枢纽建设时序方案。本文作者根据我国铁路的实际情况，为了科学合理地对新建线路进行审批，优化资源配置，从新建线路的碳排放、投资回报率和对中国铁路网的作用3个方面，采用主观赋权的层次分析法和客观赋权的熵值法确定各指标权重，运用综合评价法，建立铁路线路建设时序决策模型，计算各方案的时序决策结果，确定各方案的建设顺序。同时，考虑到铁路建设对国民经济的重大影响，铁路线路建设时序应该符合国家经济政策要求，提出政策系数，并通过层次分析法量化政府决策对铁路建设时序的影响，改进铁路线路建设时序模型。
1 铁路线路建设时序决策模型
1.1 铁路线路建设时序决策指标
确定铁路建设时序决策的关键问题是确定铁路线路建设时序的决策指标。影响铁路线路建设的因素较多，涉及环境、经济效益、社会效益等。本文从新建线路的碳排放、投资回报率以及新建线路对中国铁路网的作用3个方面作为铁路线路建设决策指标。
1.1.1 碳排放
用新建线路所减少的碳排放量表示新建线路的碳排放。付延冰等[12-14]基于生命周期评价理论，提出了交通线路生命周期内的碳排放计算方法。任福民等[15]依据生命周期评价理论，提出了铁路建设生命周期CO2排放量的评价框架和方法。根据任福民等[15]的研究，新建线路为全社会运输所减少的总碳排放量h可简化为
(1)
其中：f0为新建线路建设过程中总碳排放量；f1为铁路运营单位周转量的碳排放量；f2为公路运营单位周转量的碳排放量；Qi 为新建线路建成后某段线路的年运量；Li为Qi运量在新线上的运输距离；Nxz为新建线路使用年限。
1.1.2 投资回报率
新建铁路的投资年回报率R为
(2)
其中：C1为铁路运输单位周转量的运营成本；P1为铁路单位周转量的车票收入；V为铁路投资总额。
1.1.3 对中国铁路网的作用
铁路运输具有极大的网络效应，网络的连通性对铁路运输经营有很大影响。中国铁路网经过数十年的建设，形成了一个巨大的网络。当网络中的1个或者几个节点由于事故或者其他原因停止工作时，将导致与之相连的几条铁路线路瘫痪，由于各节点线路之间存在耦合关系，可能会导致其他线路或节点出现故障，最后导致网络大面积瘫痪。铁路线路建设不仅要从局部优势进行评价，而且要对新的铁路网整体性能进行分析。新建线路对中国铁路网的作用用加入新线路后中国铁路网在随机攻击下的鲁棒性表示。鲁棒性在铁路网中主要表现为当铁路网中某站点或线路由于列车事故或者其他自然灾害失效时，大部分铁路运输活动不受影响，铁路网整体的性能下降最小。根据Feng等[16-17]的研究，设铁路网的度分布密度函数为p(x)，由相对熵公式可得鲁棒性量度C为
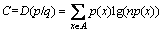(3)
其中：n为网络中节点的数量。
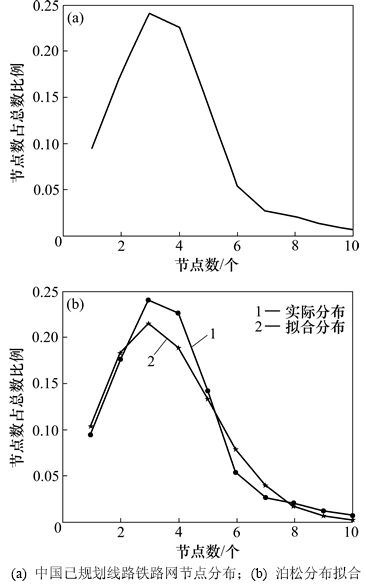
图1 中国铁路地理网度分布
Fig. 1 Degree distribution of railway geography network of China
据赵伟等[18]的研究成果，中国铁路地理网的度分布(即图结构中与某点相连接的边的数目为该节点的度，而图中各个节点度的散布情况称为度分布)近似服从泊松分布，且近似为树状网络结构。中国铁路地理网度分布如图1所示，通过对中国现在已经规划铁路网建成之后的中国铁路地理网进行分析拟合，得到中长期规划铁路网建成后的中国铁路地理网度分布泊松分布函数：
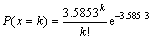(4)
将式(4)代入式(3)，可得新建线路对中国铁路网络的作用C为
,
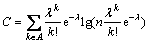(5)
1.2 铁路线路建设时序决策矩阵
将项目申请书提交的项目参数值，代入式(1)，(2)和(5)，分别计算每条计划修建线路的碳排放量、投资回报率以及对铁路网的作用这3个决策指标。设i项目第j决策指标值为xij，构造初始决策矩阵A：
(6)
将决策矩阵规范化。由于各决策指标量纲不同，数值有差异，存在着不同的单位和数量级，使得这些指标之间单位不相同，不能比较。为了避免时序决策结果中出现“大数吃小数”的错误结果，对于初始决策矩阵A，在铁路线路建设时序决策过程中对各决策指标类型归一化处理，即对初始矩阵进行量纲一变化处理。
对于极大型决策指标，
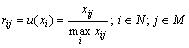(7)
对于极小型决策指标，
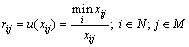(8)
初始决策矩阵A经过式(7)和式(8)量纲一变换，得到规范化的铁路线路建设时序决策矩阵R：
(9)
1.3 铁路线路建设时序决策系数
1.3.1 指标权重
决策指标权重是指各个决策指标在整体中价值的高低和相对重要的程度以及所占比例的量化值。传统的指标权重确定方法主要有主观赋权法和客观赋权法。
铁路线路建设是一项复杂的系统工程，既要考虑相关专家的丰富经验，又不能忽略各决策指标本身所蕴涵的丰富信息，因此，将主观赋权法和客观赋权法相结合来确定指标的权重，将大大减小采用单一赋权方法所带来的决策偏差。本文采用层次分析法和熵值法确定各决策指标的权重。
层次分析法(analytic hierarchy process，AHP)是将与决策有关的元素分解成目标、准则、方案等层次，在此基础上进行定性和定量分析的决策方法。根据本领域内的专家对各铁路线路建设时序决策指标重要性的比较判断，采用1~9比较尺度法构造判断矩阵P，运用特征向量法求得指标权重，通过数据分析以及一致性检验，设层次分析法归一化后的权重为wa。信息熵是利用数学概率理论来衡量信息不确定性的一种测算方法，表明数据分布越分散，其不确定性也越大。对现有的n个对象的m个决策指标计算并规范化后得到铁路线路建设时序决策矩阵R，各个指标的决策信息可以用其信息熵值
来表示。
(10)
其中：rij为R中的元素。设归一化后熵值法得到的权重为wb，结合层次分析法和熵值法，根据实际情况，在0~1范围内确定主观权重系数k，得到最终的指标权重w：
(11)
1.3.2 政策系数
采用层次分析法制定政策系数，使得最终结果更具有实际意义。政府决策者在决策前，根据该线路对地方经济主观判断各待建铁路线路的重要性，采用1~9比较尺度法，确定待建线路相互之间的重要程度，得到政策系数判断矩阵Z，运用特征值法求得政策系数。归一化后的政策系数为z。
(12)
1.4 铁路线路建设时序决策结果
本文所选取的铁路线路建设时序决策指标分别为新建线路的碳排放、投资回报率和对铁路网的重要性。各指标之间相互独立，采用线性加权综合法对n个项目进行综合评价，能确保铁路线路建设时序决策指标的公平性。根据指标权重w、规范化的决策矩阵R，指标权重和规范化决策矩阵相乘得到的铁路线路建设时序决策结果c为
(13)
其中：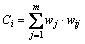
。考虑政策系数后得到最后决策结果e为
(14)
2 铁路线路建设时序决策模型的应用
本文根据郑州—新郑、郑州—开封以及郑州—焦作这3条线路的项目建设批复书对模型进行分析。根据铁路工程建设网的项目建设批复书，郑州至新郑 (43 km)城际铁路线路在近期(2024年)和远期(2034年)，其高峰小时断面分别为4 995和7 980人/h，客车流量分别为96和154对/d；郑州至开封(50 km)城际铁路线在近期(2024年)和远期(2034年)，其客流密度分别为12.50和40.10万人/d，高峰小时断面分别为0.62和1.32人/h；郑州至焦作(77.8 km)城际铁路在近期(2024年)和远期(2034年)，其客流密度分别为1 079 和1 762 万人/a，客车流量分别为58和95 对/d。
根据方琪根[19]的研究结果，高速铁路成本为0.350元/(人·km)，高速铁路客运价格为0.458元/(人·km)。据任福民等[15]的研究，铁路建设投资亿元碳排放量如图2所示。
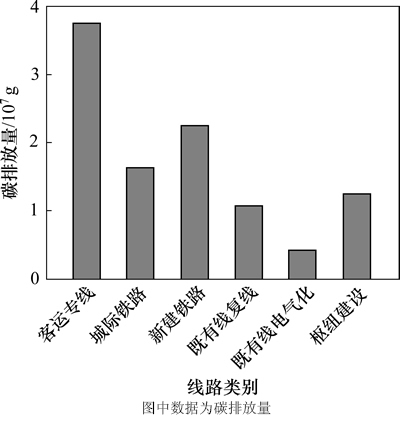
图2 铁路建设投资亿元碳排放量
Fig. 2 Carbon emissions of billion investment in railway construction
2.1 构建时序决策矩阵
根据以上数据计算各决策指标值，构建铁路线路建设时序决策初始矩阵：
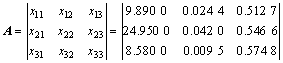
对初始决策矩阵规范化，得到规范化决策矩阵R：
2.2 确定时序决策系数
2.2.1 指标权重
根据专家主观对决策指标通过1~9比较尺度法的打分结果，构建各决策指标判断矩阵P，运用层次分析法确定主观权重wa：
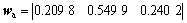
根据规范化决策矩阵R，运用熵值法计算线路碳排放、投资回报率以及线路建设对铁路网的重要性的客观权重和归一化后的客观权重wb分别为：
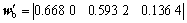
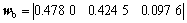
2.2.2 政策系数
这3条铁路线路均属于中原城市群轨道交通网的一部分。郑州至新郑城际铁路起自郑州枢纽郑州站，与郑焦城际铁路相连，于经济技术开发区设经开站，出站后并行于机场高速公路东侧。郑州至开封城际铁路线路西起郑州枢纽的郑州东站，与石武、徐兰客运专线、机场城际铁路衔接，东止开封市区宋城路站。郑州至新郑城际铁路和郑州至开封城际铁路均有1条普速铁路和1条高速铁路与其并行，另外还有多条高等级公路，通道内运输能力较大。郑州至焦作之间没有其他铁路连接。政府部门根据各条线路对地区经济的影响程度、民众对铁路的期盼程度等，由政府部门主观构建各线路判断矩阵Z，运用层次分析法确定政策系数z：
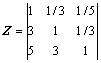
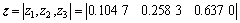
2.3 计算时序决策结果
在不考虑政策系数时，计算郑州至新郑城际铁路、郑州至开封城际铁路以及郑州至焦作铁路这3条线路在主观系数变化时的铁路线路建设时序决策得分，如表1所示。
表1 3条线路时序决策得分(不考虑政策系数)
Table 1 Timing decision results of three intercity railways without considering policy coefficient
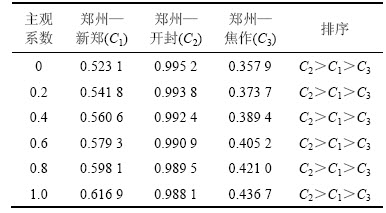
从表1可见：在不考虑政策系数的情况下，主观系数对线路时序决策结果没有影响，即在主观系数的任意取值范围内，时序决策得分大小均为C2＞C1＞C3，即优先考虑建设郑州至开封的城际铁路，再考虑建设郑州至新郑的城际铁路，最后才考虑郑州至焦作的城际铁路。
考虑政策系数时，计算郑州至开封城际铁路、郑州至新郑城际铁路以及郑州至焦作这3条线路在主观系数变化时的决策得分，如表2所示。
表2 3条线路时序决策得分(考虑政策系数)
Table 2 Timing decision results of three intercity railways considering policy coefficient
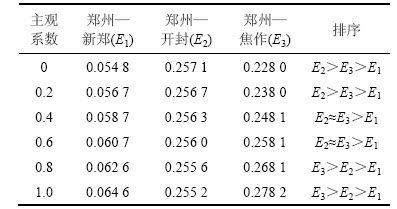
从表2可见：在考虑政策系数后，郑州至新郑的城际铁路线路的时序决策得分E1均小于其他2条线路的时序决策得分，故应该最后建设郑州至新郑的城际铁路。根据不同主观系数，郑州至开封的城际铁路线路与郑州至焦作的城际铁路线路有一些变化，当主观系数小于0.4时，优先建设郑州至开封的城际铁路；当主观系数大于0.6时，优先建设郑州至焦作的城际铁路；若主观系数为0.4~0.6，则在条件允许的情况下，2条线路可以考虑同时建设。
2.4 结果分析
实际上，郑州至焦作城际铁路和郑州至开封城际铁路线路均于2010-09开工建设，于2014年底开通运营，而郑州至新郑城际铁路的线路于2012年开工建设。由实际情况可知，郑州至新郑的城际铁路线路建设决策得分应该比另外2条线路的决策得分低，而郑州至开封城际铁路线路和郑州至焦作城际铁路线路的决策得分应该近似相等。3条线路时序决策得分如图3所示。决策得分越大表示线路越应优先建设。
从图3(a)可见：在不考虑政策系数的情况下，城际铁路线路时序决策评价得分从大至小为：郑州—开封，郑州—新郑，郑州—焦作，说明应优先建设郑州—开封城际铁路线路，再建设郑州—新郑城际铁路线路，最后考虑建设郑州—焦作城际铁路线路。将这3条线路的最优决策与实际情况比较，仅优先考虑建设郑州—开封城际铁路线路符合实际情况，另外2条线路决策与实际情况不符。
从图3(b)可见：在考虑政策因素后，郑州—新郑城际铁路线路时序决策评价得分最低，故最后考虑建设郑州至新郑城际铁路线路的决策不发生变化。但郑州—焦作与郑州—开封的城际铁路线路时序决策结果曲线在主观系数为0.4~0.6之间相交，说明郑州—开封和郑州—焦作城际铁路线路的建设时序决策随着主观系数的变化而变化：当主观系数大于0.6时，郑州—焦作时序决策评价得分比郑州—开封的大，此时应该优先建设郑州—焦作城际铁路线路；当主观系数小于0.4时，郑州—开封的时序决策评价得分比郑州—焦作的大，此时应该优先建设郑州—开封城际铁路线路；而当主观系数为0.4~0.6之间时，这2条线路的时序决策结果曲线接近，即这2条线路的开工建设的时间应该接近。
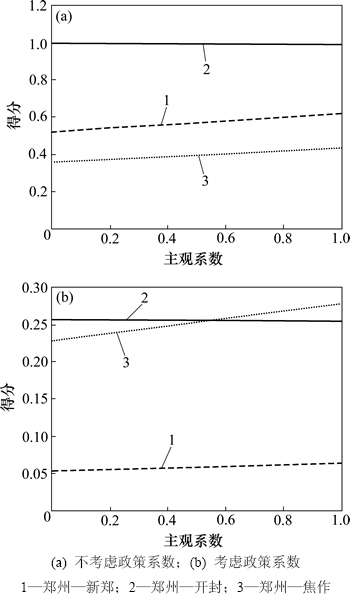
图3 3条线路时序决策结果
Fig. 3 Timing decision results of three intercity railways
由以上分析可知，在考虑政策因素后，郑州至开封城际铁路线路和郑州至焦作城际铁路线路的决策结果在主观系数为0.4~0.6时十分接近，符合实际情况。可见：为了使结果更能反映实际情况，建议主观系数为0.4~0.6。
3 结论
1) 提出以一种铁路线路建设时序决策模型。考虑新建线路的碳排放、投资回报率和对铁路网的作用，采用主观赋权的层次分析法和客观赋权的熵值法，引入主观系数，确定各决策指标的权重，建立铁路线路建设时序决策模型；根据铁路线路建设的实际情况，提出了政策系数，改进铁路线路建设时序决策模型。
2) 提出政策系数及计算方法。当忽略政策因素的影响时会使决策结果与实际需要不符，在确定线路建设时序时，可以运用层次分析法量化经济政策对铁路线路建设时序决策的影响。
3) 提出一种将主观和客观相结合的赋权法。将层次分析法和熵值法相结合，通过引入主观系数确定指标权重，主观系数为0.4~0.6时较合适。
参考文献：
[1] 冯林祥, 宋来民, 苏敬之. 关于铁路基本建设投资时序的探讨[J]. 北方交通大学学报, 1994, 18(3): 356-360.
FENG Linxiang, SONG Laimin, SU Jingzhi. Discussion on railway infrastructure investment timing[J]. Journal of North Jiaotong University, 1994, 18(3): 356-360.
[2] 何学刚. 四川对外铁路快速通道建设时序研究[J]. 铁道工程学报, 2008, 25(8): 23-26.
HE Xuegang. Research on the time sequence of external railway rapid passage construction in Sichuan[J]. Journal of Railway Engineering Society, 2008, 25(8): 23-26.
[3] 钟新, 饶武. 福厦沿海铁路通道建设时序研究[J]. 交通运输工程与信息学报, 2012, 10(2): 34-38.
ZHONG Xin, RAO Wu. Research on the construction schedule of Fuzhou—Xiamen coastal railway transportation corridor[J]. Journal of Transportation Engineering and Information, 2012, 10(2): 34-38.
[4] SONG Ping, YANG Qifeng. Empirical research onconstruction scheduling for urbanrail transit network[C]// Wireless Communications, Networking and Mobile Computing. Dalian, China: IEEE, 2008: 1-5.
[5] 吴其刚, 杨建军, 高明明. 城际铁路建设准入及时序决策模型研究[J]. 铁道工程学报, 2009, 26(10): 102-107.
WU Qigang, YANG Jianjun, GAO Mingming. Researches on the admission and sequential decision-making model for intercity railroad construction[J]. Journal of Railway Engineering Society, 2009, 26(10): 102-107.
[6] 郭延永, 刘攀, 吴瑶. 城市轨道交通建设时序确定方法[J]. 武汉理工大学学报, 2013, 35(6): 75-80.
GUO Yanyong, LIU Pan, WU Yao. Development of a method for the construction schedule of urban rail transit lines[J]. Journal of Wuhan University of Technology, 2013, 35(6): 75-80.
[7] 郭延永, 刘攀, 吴瑶. 基于累计前景理论的城市轨道交通建设时序[J]. 交通运输系统工程与信息, 2013, 13(4): 29-35.
GUO Yanyong, LIU Pan, WU Yao. Construction sequence of urban rail transit system based on cumulative prospect theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2013, 13(4): 29-35.
[8] LUO Xiaoqiang, GUO Yanyong, WU Yao. The timing of urban rail transit construction based on the weighted gray correlation [J]. Applied Mechanics and Materials, 2011, 97: 1189-1194.
[9] Greg D, Asregedew W, David H, et al. Advanced linear scheduling program with varying production rates for pipeline construction projects[J]. Automation in Construction, 2012, 27: 99-110.
[10] TANG Yuanjie, LIU Rengkui, SUN Quanxin. Schedule control model for linear projects based on linear scheduling method and constraint programming[J]. Automation in Construction, 2014, 37: 22-37.
[11] 王振报, 陈艳艳, 韩冬. 城市客运交通枢纽建设时序优化方法[J]. 吉林大学学报(工学版), 2012, 42(4): 899-903.
WANG Zhenbao, CHEN Yanyan, HAN Dong. Optimization method of project construction scheduling for intermodal hub[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(4): 899-903.
[12] 付延冰, 刘恒斌, 张素芬. 高速铁路生命周期碳排放计算方法[J]. 中国铁道科学, 2013, 34(5): 140-144.
FU Yanbing, LIU Hengbin, ZHANG Sufen. Carbon dioxide emission assessment in high-speed railway construction[J]. China Railway Science, 2013, 34(5): 140-144.
[13] 宋晓东, 付延冰, 刘恒斌, 等. 基于生命周期评价的高速铁路减排效果[J]. 中南大学学报(自然科学版), 2014, 45(9): 3301-3307.
SONG Xiaodong, FU Yanbing, LIU Hengbin, et al. Carbon dioxide emission reduction of high-speed railway[J]. Journal of Central South University (Science and Technology), 2014, 45(9): 3301-3307.
[14] SONG Xiaodong, FU Yanbing, CHEN Zhiya, et al. Environmental impact evaluation for high-speed railway[J]. Journal of Central South University, 2014, 21(6): 2366-2371.
[15] 任福民, 郭鑫楠, 梁锐, 等. 铁路建设生命周期二氧化碳排放评价[J]. 北京交通大学学报, 2013, 37(1): 115-119.
REN Fumin, GUO Xinnan, LIANG Rui, et al. Carbon dioxide emission assessment in railway construction[J]. Journal of Beijing Jiaotong University, 2013, 37(1): 115-119.
[16] FENG Fenling, WANG Lei. Robustness measure of China’s railway network topology using relative entropy[J]. Discrete Dynamics in Nature and Society, 2013: 1-9.
[17] FENG Fenling, TANG Ziwen, WANG Lei. A fault tolerance optimization model of the china railway geographic network topological structure[J]. Discrete Dynamics in Nature and Society, 2015: 1-9.
[18] 赵伟, 何红生, 林中材, 等. 中国铁路客运网网络性质的研究[J]. 物理学报, 2006, 55(8): 3906-3911.
ZHAO Wei, HE Hongsheng, LIN Zhongchai, et al. The nature of the China railway passenger transport network research[J]. Acta Physica Sinica, 2006, 55(8): 3906-3911.
[19] 方琪根. 高速铁路运营成本的作业成本法测算研究[J]. 铁道科学与工程学报, 2006, 3(5): 87-92.
FANG Qigen. Research on activity-based costing of operation cost account in high speed railway[J]. Journal of Railway Science and Engineering, 2006, 3(5): 87-92.
(编辑 陈灿华)
收稿日期：2015-02-10；修回日期：2015-04-08
基金项目(Foundation item)：国家自然科学基金资助项目(71371193) (Project(71371193) supported by the National Natural Science Foundation of China)
通信作者：姬志洲，副研究员，从事交通运输规划与管理研究；E-mail: jzz@csu.edu.cn
