DOI: 10.11817/j.issn.1672-7207.2016.01.011

数控强力刮齿加工误差分析及补偿

郭二廓¹，洪荣晶^{1, 2}，黄筱调^{1, 2}，方成刚^{1, 2}

(1. 南京工业大学 机械与动力工程学院，江苏 南京，211800；

2. 江苏省工业装备数字制造及控制技术重点实验室，江苏 南京，211800)

摘要：在数控强力刮齿加工过程中，针对因刮齿机床各项误差耦合造成的加工精度不高的问题，基于空间交错轴斜齿轮啮合原理，建立内齿圆柱齿轮强力刮齿加工的数学模型。由包含误差的齿面方程与理论齿面方程对比，得到机床各调整参数误差与全齿形法向偏差的变化规律，通过建立机床各调整参数误差与齿形偏差关联函数，提出一种基于建立齿形误差敏感系数矩阵的误差补偿方法。以一个内齿圆柱齿轮的刮齿加工计算实例验证本文所提方法的可行性。研究结果表明：因机床调整参数误差造成的齿形偏差得到了高精度补偿和修正，有效提高了强力刮齿的加工精度。

关键词：数控加工；强力刮齿；误差分析；补偿方法

中图分类号：TH132       文献标志码：A         文章编号：1672-7207(2016)01-0069-08

Error analysis and compensation for CNC power skiving

GUO Erkuo¹, HONG Rongjing^{1, 2}, HUANG Xiaodiao^{1, 2}, FANG Chenggang^{1, 2}

(1. College of Mechanical and Power Engineering, Nanjing Tech University, Nanjing 211800, China;

2. Jiangsu Key Laboratory of Digital Manufacturing for Industrial Equipment and Control Technology,

Nanjing 211800, China)

Abstract: To reduce the tooth profile deviations of power skiving processing caused by machine setting parameters error, a mathematic model of power skiving for working internal cylinder gear was established based on the engagement principle of crossed helical gear. The relationships were obtained between machine setting parameters error and tooth profile deviations by the difference of error tooth profile and theoretical tooth profile. An error compensation method was proposed for solving the sensitive coefficient matrix of tooth error. The validity of this method for power skiving was numerically demonstrated as working an internal cylinder gear for example. The results show that the tooth deviations caused by machine setting parameters error are corrected and the accuracy is improved.

Key words: CNC machining; power skiving; error analysis; compensation method

当前国内外圆柱齿轮的加工方法主要以滚齿、插齿、铣齿和拉齿为主，但随着齿轮切削加工技术向着高精度、高效率、绿色环保的方向发展，迫切需要研究开发齿轮加工的新工艺和新技术。近年来，随着数字化控制技术、现代机床设计制造技术、机电一体化技术、新刀具涂层技术和高速切削技术的进一步发展，使得强力刮齿加工这种全新概念的切齿加工方法成为可能。它的生产效率要高于滚齿和插齿加工的生产效率，尤其是对小模数内齿轮加工，强力刮齿加工方法相对滚齿和插齿加工方法有更高的效率，一般可提高4倍以上，加工精度也可提高1~2个等级^[1]。SPATH等^[2]提出了高效的刮齿加工技术，随后STADTFELD等^[3-4]把强力刮齿作为一种当代齿轮加工方法，对强力刮齿的概念、刮齿刀具、刮齿加工原理进行了研究。美国Gleason公司采用了这种高效圆柱齿轮加工技术，将这种全新齿形加工概念称之为强力刮齿(Power Skiving)，德国WERA公司提出的Scudding技术也很好地适应了圆柱齿轮的加工要求，两者均推出了基于该技术的数控机床，但出于技术上的保密，该技术一直被国外垄断。VOLKER等^[5]为了进一步改进和完善刮齿加工过程，尤其是加强刮齿加工的可靠性研究，给出了加工过程运动学仿真、切屑成型机理以及刮齿加工可靠性的研究结果。此外，HARTMUT等^[6-7]提出了一种用于强力刮齿加工方法的刮齿刀具及其装置，同时针对刮齿加工中出现的刀具磨损不匀的问题，提出了一种刮齿加工中调整刀具切削位置使载荷均布的工艺方法。为了满足国内对高档数控齿轮加工装备的需求，李佳等^[8]提出了一种圆柱齿轮剐齿加工方法，该方法将刀具的刃形设计成与工件齿形共轭形状，用多轴运动控制器控制工件和刀具的旋转，配合刀具的轴向和径向进给，形成剐削作用完成工件轮齿表面的切削成形，可在无退刀槽条件下可完成非贯通渐开线内齿的加工。随后，CHEN等^[9-10]对直齿剐齿刀的结构设计和理论方法进行了研究，基于曲面共轭原理，建立剐齿刀各刀面的数学模型，提出了一种无理论齿形误差直齿剐齿刀的设计方法。最后，CHEN等^[11]为了满足剐齿加工中机床配置和控制系统要求，基于SIEMENS 840D数控系统对剐齿加工同步控制进行了研究，提出了一种改善控制精度的同步运动控制方法。此外，吴序堂等^[12-14]提出的将机床的综合误差视为微小误差变动量的线性叠加是本文误差补偿方法的基础。强力刮齿加工方法作为一种全新高效高精的加工方法，需要对其进行深入地研究。本文作者在前人研究的基础上，以内圆柱齿轮加工为例，介绍数控强力刮齿加工的原理，建立内齿轮加工数学模型，对数控强力刮齿加工的误差进行分析，并提出一种基于求解齿形误差敏感系数矩阵的补偿方法，得到机床调整参数的最优解，实现对刮齿加工误差的高精度补偿和修正。

1  数控强力刮齿加工

1.1  数控强力刮齿加工原理

强力刮齿加工是采用滚、插齿为一体的切削方法，用于加工内、外圆柱齿轮，在切齿加工过程中，切齿刀具既相当于滚刀又相当于插齿刀，其切削方式为工件和刀具连续旋转，将滚齿和插齿运动相结合来进行切齿加工。

强力刮齿法的加工原理实质上相当于1对交错轴齿轮副的啮合传动，通过刀具和齿坯的强迫啮合运动来实现切齿加工。刀具相对于齿坯有一轴交角Σ，它与工件、刀具的螺旋角有关，三者之间关系为

Σ=β₁±β₂                (1)

式中：β₁为刀具螺旋角；β₂为工件螺旋角；加工内齿轮时，“+”表示刀具与工件旋向相反；“-”表示刀具与工件旋向相同。

在切削点处，刀具的切削速度v₁被分解成切向速度分量v_1t和轴向速度分量v_1a，v_1t与工件上切削速度v₂合成后形成切削点的切向速度v_t，再将它与v_2a合成后形成最终的切削速度v，通过刀具、工件高速旋转和工件沿轴向进给，切削速度v随切削点在刀刃上的不同位置而变化，从而实现具有“剜”和“削”双重功效的切削过程^[6]，并且每次切削量非常小，此时，从齿坯上切下的微小条形切屑沿齿廓方向排出，经过千万次切削完成对整个齿面的加工。

根据空间交错轴齿轮啮合原理，需要通过刀具、工件的高速旋转以及工件或刀具沿着工件轴线方向运动来实现强力刮齿加工。图1所示为内齿圆柱轮强力刮齿加工示意图，图中：刀具转速为ω₁；工件转速为ω₂；工件沿轴向进给速度为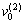。因该轴向进给速度影响，刀具与工件之间的啮合关系就需要通过附加转动来提供正确的啮合关系，以保证加工出正确的齿形。考虑的刀具附加转动之后，其角速度变化量为

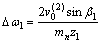              (2)

式中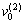：为工件沿轴线方向进给速度；m_n为工件法向模数；z₁为刀具齿数。

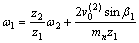            (3)

反之，若通过工件进行附加运动，由工件与刀具之间的啮合关系，工件的角速度变化量为

         (4)

式中：i₁₂为刀具与工件之间的传动比；z₂为工件齿数。

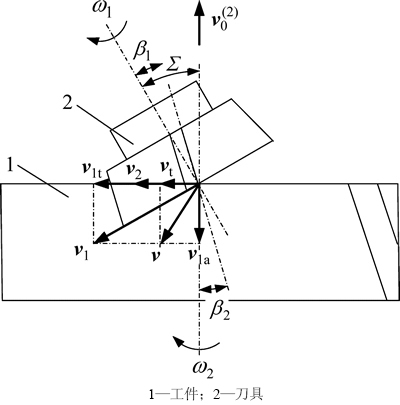
图1  内齿圆柱齿轮强力刮齿加工示意图

Fig. 1  Kinematical principle of power skiving for internal cylindrical gear

则刀具、工件转速以及工件沿轴向进给速度之间关系为

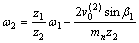            (5)

1.2  强力刮齿空间坐标系

图2所示为分析刮齿加工空间啮合运动时采用的坐标系，其中：S(O-x, y, z)坐标系与刀具固连，z轴与刀具的回转轴线重合，S_p(O_p-x_p, y_p, z_p)坐标系与工件固连，z_p轴与工件的回转轴线重合，z轴与z_p轴的轴线之间的夹角为Σ，x轴与x_p轴重合，两轴线的最短距离OO_p等于中心距a。

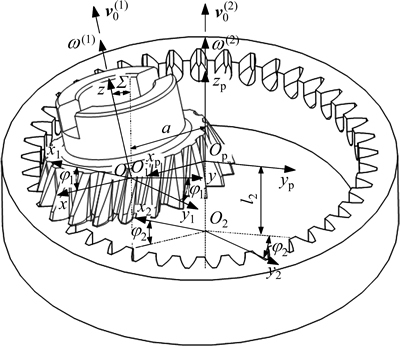
图2  刮齿加工空间啮合坐标系

Fig. 2  Coordinate systems of power skiving

坐标系S₁(O₁-x₁, y₁, z₁) 与刀具固联，坐标系S₂(O₂-x₂, y₂, z₂)与工件固联，在起始位置时，它们分别与S及S_p重合。刀具以匀角速度ω⁽¹⁾绕z轴转动，并以速度v₀⁽¹⁾沿z_p轴匀速移动；工件以匀角速度ω⁽²⁾绕z_p轴转动。从起始位置经过一段时间后，S₁与S₂运动到图1中位置，OO₁=l，则刀具绕z轴转过φ₁，工件绕z_p轴转过φ₂。由空间坐标变换，可求得上述各坐标系之间的变换关系。

由刀具坐标系S₁到工件坐标系S₂的变换关系为

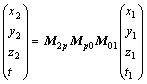          (6)

式中：

；

；

；

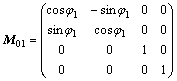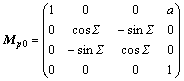φ₁为刀具绕z轴转过的角度；φ₂为工件绕z_p轴转过的角度；a为刀具与工件之间的安装中心距；l₂为工件的轴向移动距离。

1.3  齿面方程的建立

刮齿加工过程可视为一对空间交错轴齿轮副啮合传动来研究，假设该齿轮副是作点接触的共轭齿面Σ⁽¹⁾和Σ⁽²⁾，则它们在接触点处一定满足下面的啮合方程式^[12-13]：

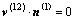                 (7)

式中：v⁽¹²⁾为刀齿与工件的相对运动速度；n为啮合齿面法线矢量。

设刀具齿面Σ⁽¹⁾在坐标系S₁中的方程式为

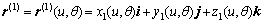  (8)

式中：x₁，y₁和z₁为刀齿坐标点；(u,θ)为齿面的曲线参变数；p为螺旋参数。则齿面上任一点的法线矢量n⁽¹⁾为

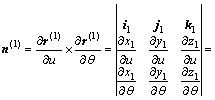
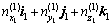            (9)

则n⁽¹⁾在固定坐标系S中的3个分量，和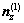经坐标变换后得到

       (10)

设在空间有一点P，它在固定坐标系S中的坐标为(x, y, z)，则P点随刀具运动时的速度v⁽¹⁾为

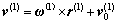            (11)

P点随齿轮工件运动时的速度v⁽²⁾为

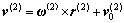            (12)

则刀具与工件在P点的相对运动速度v⁽¹²⁾为

  (13)

所以

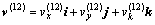        (14)

式中：

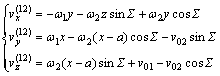
联立式(7)，(10)及(14)，可得到用坐标(x, y, z)表示的啮合方程式为

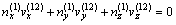       (15)

由刀具坐标系S₁到工件坐标系S₂的变换关系为

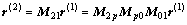      (16)

将式(15)与式(16)联立，则得齿面Σ⁽²⁾的参数形  式为

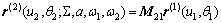    (17)

2  数控强力刮齿误差分析

数控强力刮齿中影响齿形加工精度的因素很多，其中很重要的一项因素来源于机床调整参数误差，由于机床的各项调整参数对齿形误差的影响相互关联，且耦合关系复杂，使得齿形加工误差的修正补偿困难。通过研究发现，对强力刮齿加工误差较为敏感的机床调整参数主要包括刀具安装角度误差ΔΣ、刀具安装轴向误差Δa、高速轴同步误差Δn₁和Δn₂，针对这4个机床调整参数对刮齿加工精度的影响进行分析。

2.1  误差齿面方程建立

在进行数控强力刮齿加工时，刮齿刀具的安装误差ΔΣ和Δa和2个高速轴的同步误差Δn₁和Δn₂都会反映到工件的齿形精度上，即当机床的调整参数存在误差时，实际加工出的齿形就会偏离理论设计齿形，误差值设为δ_k=[ΔΣ, Δa, Δn₁, Δn₂]，则含有误差的机床调整参数可表示为

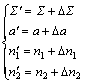              (18)

各项机床误差综合影响得到的实际齿面方程为

   (19)

    图3所示为刮齿刀展成运动包络出的内齿齿形。式(17)和式(19)为4个参变量u₂，θ₂，n₁和n₂表示的齿面表达式，因n₁=i₁₂n₂，通过离散u₂，θ₂和n₁的取值便可计算出齿面上任意一点的法矢和坐标，由刀具与工件的展成包络运动(见图3)得到含误差的齿形数据点与理论齿形数据点对比，则齿形上任意一点的误差可由理论齿形和实际齿形的法向偏差δr_i来表示：

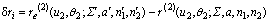                       (20)

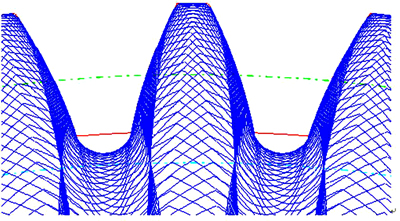
图3  刮齿刀展成运动包络出的内齿齿形

Fig. 3  Tooth profile of internal gear performed by skiving cutter

2.2  刮齿加工误差分析

由微观等效原理，刮齿加工误差可以用机床调整参数的微小变量来表示，分别对机床调整参数进行微调，并假设位移调整参数的扰动误差为+0.05 mm，角度调整参数扰动误差为+0.2°，速度调整参数扰动误差为+0.05 r/min。由各调整参数的扰动误差变动量可得齿形误差的变化规律，并以此扰动量作为累积误差的初始值。

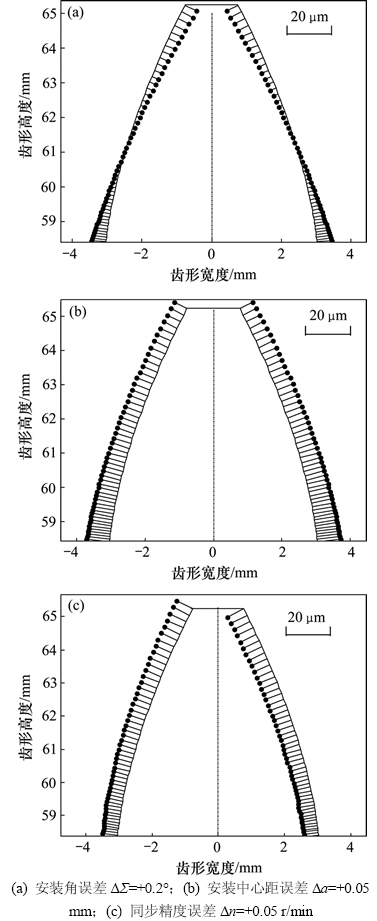
图4  机床调整参数微小误差对齿形精度的影响

Fig. 4  Relationship between micro-small setting errors and tooth deviations

图4所示为机床调整参数微小误差对齿形精度的影响。图5所示为机床调整参数微小误差对单侧齿形精度的影响。由图4(a)和图4(b)可知：安装角误差ΔΣ和安装中心距误差Δa对左右齿形精度的影响效果相同，呈对称分布(齿形内侧为正值，外侧为负值)，此时，安装角误差ΔΣ造成的齿形偏差在小于分度圆的齿形部分过切，而在大于分度圆的齿形部分欠切；安装中心距误差Δa使得左右侧齿形同时过切，且左右对称；同步精度误差Δn使得左侧齿形部分整体过切，右侧齿形部分整体欠切(见图4(c))。

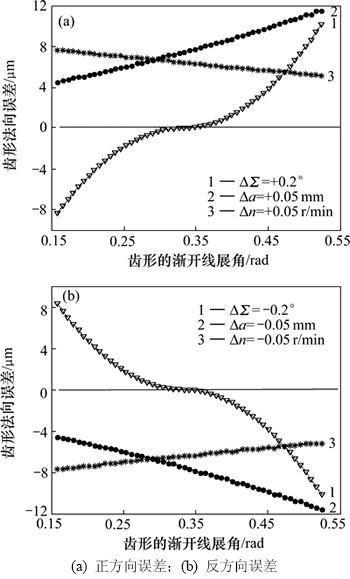
图5  机床调整参数微小误差对单侧齿形精度的影响

Fig. 5  Relationship between micro-small setting errors and tooth deviations of single flank

3  数控强力刮齿误差补偿

为了保证刮削出的齿轮精度满足要求，在加工前需将各工艺参数调整到合理的范围内，基于建立敏感系数矩阵法针对加工中影响齿形精度的机床安装参数误差进行补偿。

首先，假设齿形上任意1点的误差是各项机床调整参数微小变化引起的单个齿形误差的叠加，即每项安装误差对应的微小误差变动量是线性叠加的，则有

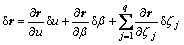       (21)

因为向量和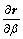都是垂直于齿面法矢，则其法向误差为

            (22)

整个齿形上的法向误差表示成矩阵形式为^[14-16]

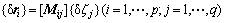     (23)

式中：n为齿面数据点的法向矢量；r_i为理论齿面在第i点的表达式；δr_i为理论齿面在第i点的法向误差；δζ_j为第j项机床调整参数的微小变化量；[M_ij]为齿形上第i点法向误差随第j项机床调整参数变化的敏感系数矩阵。

然后，由式(23)求解得到敏感系数矩阵[M_ij]，并将该敏感系数矩阵作为初始变换矩阵，对于测量得到的齿面法向误差矩阵点δr_i，根据最小二乘的线性回归方法，可以求解出需要调整的机床参数修正量δζ_j，即

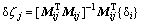           (24)

最后，通过重新调整机床安装参数，实现对加工误差值的高精度修正补偿。

4  实例分析

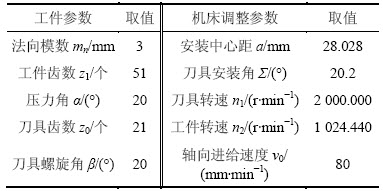
以1个内齿圆柱直齿轮的刮齿加工为例，进一步验证本文所提方法可行性。表1所示为刀具、工件(内直齿)和机床调整参数。人为给定误差扰动量进行分析，安装中心距的误差为+0.05 mm，安装角度误差为+0.2°，速度同步运动精度误差为+0.05 r/min，则可以得到这些误差综合影响之下的齿形偏差，如图6所示，修正补偿前的左侧齿形最大法向偏差为21.5 μm，右侧齿形最大法向偏差为5.4 μm。

表1  刀具、工件(内直齿)和机床调整参数

Table 1  Basic parameters of skiving cutter and workpiece

采用上述敏感系数矩阵法对刮齿加工参数进行修正补偿后，可以得到机床调整参数的变化量。图7所示为求解敏感系数矩阵法过程中的计算结果，分别为补偿前左右齿形误差δr_i、左右齿形端面法矢n、敏感系数矩阵M_ij和补偿后左右齿形误差δ。

根据所求解出的敏感系数矩阵，由式(24)可以求出机床调整参数修正量δζ_a=-0.05 mm，δζ_Σ=-0.2°，δζ_n1=0和δζ_n2=-0.05 r/min，如表2所示，该方法得到机床调整参数修正量δζ_a，δζ_Σ，δζ_n1，δζ_n2与人为给定的误差扰动量ΔΣ，Δa和Δn相吻合。

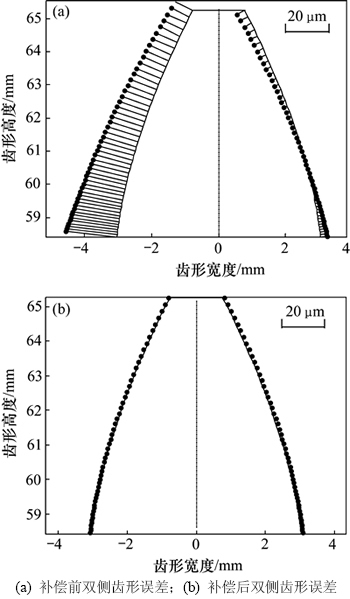
图6  补偿前和补偿后的齿形误差

Fig. 6  Tooth deviations before and after correction

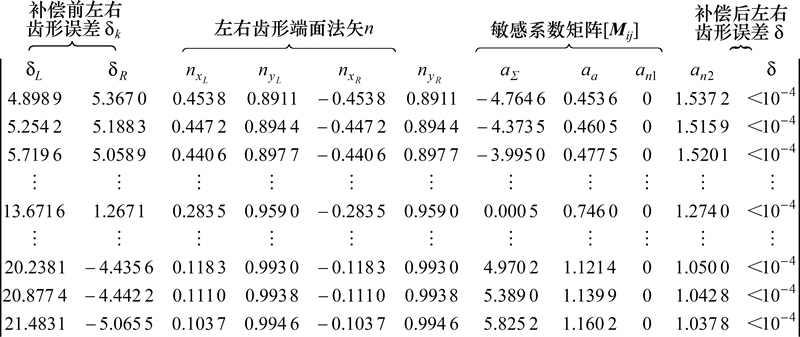
图7  求解敏感系数矩阵法计算结果

Fig. 7  Part of calculation results in solving sensitivity coefficients matrix

图8所示为补偿前后的齿形误差对比。将表2中修正后的机床参数代入到式(20)中，得到补偿后的左、右齿形的最大法向偏差小于0.1 μm，修正效果极佳，将原有的刮齿误差补偿修正到合理的加工精度范围内，理论上可完全消除误差。验证了本文所提刮齿加工误差补偿方法的可行性。

表2  修正后的机床调整参数

Table 2   Setting parameters of machine tool after correction

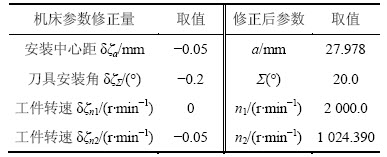
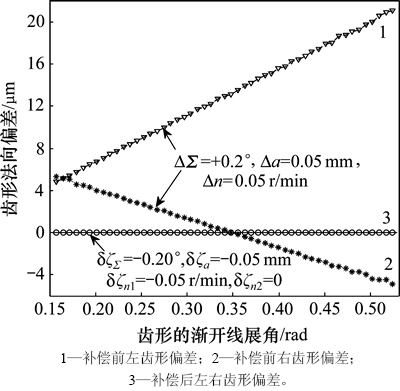
图8  补偿前后的齿形误差对比

Fig. 8  Tooth deviations before and after correction

5  结论

1) 建立内齿圆柱齿轮强力刮齿加工的数学模型，介绍了数控强力刮齿加工的原理，得到了各项机床调整参数误差对全齿形法向偏差的影响规律，为刮齿加工误差分析和补偿提供了正确调整初值，并得到刮齿加工各调整参数误差与齿形偏差的关联函数。

2) 提出了一种基于建立齿形误差敏感系数矩阵的误差补偿方法。该误差补偿方法假设每项调整参数对应的微小误差变动量是线性叠加的，通过求解出敏感系数矩阵，根据实际测量得到刮齿齿形误差值，反求出机床的调整参数。本文所提补偿方法具有通用性，可以实现对内、外和直、斜齿的强力刮齿加工误差的高精度补偿，为数控强力刮齿加工的推广应用提供了理论基础。

参考文献：

[1] KOBIALKA C. Contemporary gear pre-Machining solutions[J]. Gear Solutions, 2013(4): 43-49.

[2] SPATH D, HUHSAM A. Skiving for high-performance machining of periodic structures[J]. Annals of the CIRP, 2002, 51(1): 91-94.

[3] STADTFELD H. Power skiving of cylindrical gears on different machine platforms[J]. Gear Technology, 31(1): 52-62.

[4] FLEISCHER J, BECHLE A, KUHLEWEIN C. High performance gearing by skiving[C]// CIRP 2nd International Conference on High Performance Cutting(HPC). Vancouver, Canada: University of British Columbia, 2006: 1675-1678.

[5] VOLKER S, CHIRSTTOPH K, HERMANN A. 3D-FEM modeling of gear skiving to investigate and chip formation mechanisms[J]. Advanced Materials Research, 2011, 223: 46-55.

[6] HARTMUT M, OLAF V. Robust method for skiving and corresponding apparatus comprising a skiving tool: 20120328384A1[P]. 2012.

[7] HARTMUT M, OLAF V. Semi-completing skiving method and device having corresponding skiving tool for executing a semi-completing skiving method: 20130071197A1[P]. 2013.

[8] 李佳, 陈新春, 张鸿源. 圆柱齿轮剐齿技术[J]. 机械工程学报, 2011, 47(19): 193-198.

LI Jia, CHEN Xinchun, ZHANG Hongyuan. Slicing technology for cylindrical gears[J]. Chinese Journal of Mechanical Engineering, 2011, 47(19): 193-198.

[9] CHEN Xinchun, LI Jia, LOU Benchao. A study on the design of error-free spur slice cutter[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(1): 727-738.

[10] CHEN Xinchun, LI Jia, LOU Benchao, et al. Effect of the cutter parameters and machining parameters on the interference in gear slicing[J]. Chinese Journal of Mechanical Engineering, 2013, 26(6): 1118-1126.

[11] CHEN Xinchun, LI Jia, LOU Benchao. Research of the synchronous motion control for the gear slicing CNC machine tool based on SIEMENS 840D[J]. Advanced Science Letters, 2012, 5(1): 687-691.

[12] 吴序堂. 齿轮啮合原理[M]. 2版. 西安: 西安交通大学出版社, 2009: 126-172.

WU Xutang. Principle of gearing[M]. 2nd ed. Xi’an: Xi’an Jiaotong University Press, 2009: 126-172.

[13] LITVIN F, FUENTES A. Gear geometry and applied theory[M]. 2nd ed. New York: Cambridge University Press, 2004: 33-127.

[14] SHIH Y P, CHEN S D. A flank correction methodology for a five-axis CNC gear profile grinding machine[J]. Mechanism and Machine Theory, 2011, 47: 31-45.

[15] SHIH Y P, CHEN S D. Free-form flank correction in helical gear grinding using a five-axis computer numerical control gear profile grinding machine[J]. ASME Journal of Manufacturing Science and Engineering, 2012, 134: 041006.

[16] 唐进元, 聂金安, 王智泉. 螺旋锥齿轮HFT 法加工的反调修正方法[J]. 中南大学学报(自然科学版), 2012, 43(6): 2142-2149.

TANG Jinyuan, NIE Jinan, WANG Zhiquan. Reverse correction of spiral bevel gear HFT method[J]. Journal of Central South University (Science and Technology), 2012, 43(6): 2142-2149.

(编辑  罗金花)

收稿日期：2014-12-20；修回日期：2015-02-20

基金项目(Foundation item)：国家自然科学基金资助项目(51175242)；江苏省科技成果转化专项资金资助项目(BA2012031) (Project(51175242) supported by the National Natural Science Foundation of China; Project(BA2012031) supported by the Special Fund of Jiangsu Province for the Transformation of Scientific Research achievements)

通信作者：郭二廓，博士研究生，从事数控加工技术、齿轮先进加工制造工艺及其装备研究；E-mail: guoerkuo@sina.com