复杂边坡非圆弧滑动面求解的类电磁机制算法

张科，曹平

(中南大学 资源与安全工程学院，湖南 长沙，410083)

摘要：针对复杂边坡非圆弧滑动面求解，结合双层搜索机制，将类电磁机制算法作为第1层搜索方法，将粒子数较少的类电磁机制算法或复合形法作为第2层搜索方法。研究结果表明：本文的2种算法与其他算法相比所得结果都比较接近，证明本文方法的有效性；左右交点位置对安全系数影响的敏感度于滑动面其他节点的低；复合形法作为第2层搜索方法，其计算精度比采用类电磁机制算法的略高，但迭代次数成倍增加；算例中可能存在若干条滑动面，安全系数相差很小，但滑动面位置有差别。

关键词：边坡稳定；非圆弧滑动面；双层搜索方法；类电磁机制算法；复合形法

中图分类号：TU 443          文献标志码：A         文章编号：1672-7207(2011)10-3125-06

Locating non-circular critical slip surfaces by

electromagnetism-like algorithm

ZHANG Ke, CAO Ping

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: Due to the difficulty of locating non-circular critical slip surfaces, search method with two-layer structure was used, electromagnetism-like algorithm was taken as the first layer search method, electromagnetism-like algorithm with small population or complex method was taken as the second layer search method. The results show that the critical slip surfaces and factors of safety obtained by the two methods are similar to those by other methods. The effectiveness and efficiency of the algorithm is proved. The position of the two exit points has little influence on factors of safety, calculation accuracy of the second layer search with complex method is slightly higher than that with electromagnetism-like algorithm, but the number of iteration double increases. There may be small differences in factor of safety, but large differences in the location of critical slip surface.

Key words: slope stability; non-circular critical slip surface; search method with two-layer structure; electromagnetism-like algorithm; complex method

目前在边坡工程计算及规范中通常以极限平衡法为主，用极限平衡法分析边坡稳定性的关键问题是确定最危险滑动面的位置和相应的最小安全系数，而滑动面常被简化为平面、圆弧型或对数螺旋型。在工程实际中主要为非匀质边坡，由于岩土体性质和坡面形状复杂，假设边坡的滑移模式难以反映边坡滑移的实际状态，而且边坡临界滑动面的搜索属于非线性优化问题，可能存在多个极值，很容易陷入局部极小值^[1]。Nguyen^[2]采用单纯形法，Chen等^[1]采用牛顿法，Greco等^[3-4]采用蒙特卡罗法，Chen等^[5-6]采用随机搜索法进行非圆弧滑动面的搜索。但是，由于传统优化方法本身存在的局限性，容易陷入局部极小值，或者计算效率比较低。近年来，随着计算机技术的发展，遗传算法^[7-8]、模拟退火算法^[9]、粒子群算法^[10-11]、蚁群算法^[12]等智能优化算法被相继应用于边坡稳定性分析，取得了较好的效果。类电磁机制算法^[13-15]是Birbil和FANG于2003年受电磁场中电子吸引和排斥机制的启发而提出的新型全局优化算法。现有研究表明^[13]：与其他算法相比，类电磁机制算法具有更强大的搜索能力。在此，本文作者将类电磁机制算法应用于复杂边坡非圆弧滑动面的求解。

1  类电磁机制算法

类电磁机制算法模仿电磁场中带电粒子的吸引和排斥现象，引导粒子向最优解方向移动^[13]。带电粒子的吸引-排斥示意图见图1。算法步骤如下。

(1) 初始化。从可行域中随机产生m个粒子，计算相应的函数值f(xⁱ)，(i=1，2，…，m)。将目标函数值最优的点记作x^best。

(2) 局部搜索。本文只对最优粒子进行局部搜索，在取值范围内给定随机步长，对粒子的每一维进行线性搜索，若在n_lsiter次迭代步数内，找到更好的解就停止，否则，保持初始值不变。

(3) 计算合力。根据式(1)计算各粒子所带的电荷量qⁱ。

      (1)

类似库仑定理，作用在粒子i上的合力Fⁱ计算如下：

   (2)

图1  吸引-排斥示意图

Fig.1  An example of attract-repulse effect

(4) 粒子移动。粒子根据合力Fⁱ的方向，以1个随机步长移动。

      (3)

式中：λ为[0，1]的随机数；R_NG表示粒子向上边界或下边界移动的可行步长。当Fⁱ/||Fⁱ||＞0时，向上边界移动；反之，则向下边界移动。

(5) 结束条件。通常以最大迭代次数n_maxiter作为类电磁机制算法的结束条件。

2  临界滑动面优化搜索算法

2.1  边坡稳定性计算方法

本文采用简化Janbu法，具体公式可见文献[14]。非圆弧滑动面示意图见图2，它可以由n个点控制，临界滑动面的求解实际上就是n维函数的优化问题。V₁点和V_n点的纵坐标y₁和y_n可由边坡几何形状求得，其他各点的横坐标x₂，x₃，…，x_n-1可以通过将(x_n-x₁)均分得到，即，(i=2，3，…，n-1)。滑动面的求解可以表述为：

         (4)

图2  非圆弧滑动面示意图

Fig.2  Defining a non-circular failure surface

滑动面需满足一些约束条件：

(1) 滑动面左、右交点必须在坡面线上，即

y_i=t(x_i)；i=1或n             (5)

(2) 其他节点必须在坡体内，即

t(x_i)＞y_i＞h(x_i)；i=2，3，…，n-1      (6)

(3) 滑面(左右交点除外)不能与坡面线相交。当坡面转折点T_k位于节点V_i-1和V_i之间时，虽然节点满足条件(2)，但节点间的滑面段仍可能与坡面线相交(如图3所示)，所以，还需满足下式：

       (7)

图3  滑面段与坡面线相交示意图

Fig.3  Diagram of intersection between slip surface and ground profile

需指出的是，将类电磁机制算法应用于非圆弧滑动面的搜索时还可能出现如下特殊情况：类电磁机制算法的步骤(4)中y_i-1经过移动后，导致V_i-1和V_i间的滑面段与坡面线相交，而Fⁱ/||Fⁱ||为正，即要求节点V_i向上移动，此时会导致不合理的滑动面出现。本文采用重新初始化y_i的方法来解决这个问题。

本文并未严格限定滑动面的形状(如上凹形)，因为在层状土中部分滑动面有可能呈凸面^[3]。

2.2  双层搜索方法

非圆弧滑动面的搜索一般使所有节点同时变化。根据式(4)，当左、右交点变动时，其余节点的横坐标随之改变，并导致纵坐标取值范围发生改变。双层搜索就是先固定滑出点和滑入点，求得对应的安全系数，这是第1层搜素；再多次变动左、右交点位置，可求得边坡全局最小安全系数，这是第2层搜素。第2层搜索的目标函数为第1层求得的最小安全系数。双层搜索机制能使优化问题的维数降低，将n维的优化问题分解为n-2维和2维。在第2层搜索中由于左、右交点的位置固定，其他节点纵坐标的取值范围也就保持不变，因而复杂度降低，搜索效率大大提高。

第1层搜索可用数学模型表示为：

        (8)

第2层搜索可用数学模型表示为：

                   (9)

潘家铮^[15]最早提出了这种设想，但未编制程序。邹广电等^[16]采用模拟退火-随机搜索耦合算法实现了双层搜索，但是，模拟退火算法优化效率较低，而随机搜索缺乏有效的优化机制，也必须保证足够多的搜索次数。本文采用类电磁机制算法实现第1层搜索。类电磁机制算法通过吸引和排斥机制使粒子向最优解方向移动，算法收敛较快，适合边坡危险滑动面的搜索。第2层搜索只有2个变量，但直接影响计算效率，要求计算目标函数(调用第1层搜索算法)的次数尽量少，可以用传统的优化算法如复合形法(记为方法1，简写为CM-EM)或者粒子数较少的类电磁机制算法(记为方法2，简写为EM-EM)。关于复合形算法的原理和计算步骤可见文献[17]，在算例中将对这2种方法进行对比分析。

第1层搜索的类电磁机制算法其参数设置如下：种群数量m₁=20，局部迭代次数n_lsiter1=5，全局迭代次数n_maxiter1=100；第2层的复合形法的顶点数n=4，映射系数α=1.3，收敛精度δ=10^-3；第2层搜索的类电磁机制算法取种群数量m₂=5，局部迭代次数n_lsiter2=4，停止条件为：当最优粒子的目标函数值不发生变化时，算法停止。

3  计算实例与分析

算例1^[18]为澳大利亚计算机应用协会(ACADS)的考题EX1(c)。边坡剖面情况如图4所示，计算参数为：γ=20 kN/m³，c=3 kPa，φ=19.6°。

本文的计算结果比ACADS得出的略小，如表1所示。图4所示为STAB软件的简化Bishop法计算结果^[19]，而本文采用非圆弧滑动面，所以危险滑动面位置略有区别。

算例2选自文献[20]，含有软弱夹层，各土层物理力学参数见表2。Bolton等^[20]采用蛙跳算法，Cheng等^[11]采用粒子群算法对本算例进行了研究。由本文2种方法求得的临界滑动面及相应的安全系数与Bolton和Cheng所得的结果非常接近，如图5和表3所示。

算例3选自文献[21]，各土层物理力学参数见表4。Arai等^[23]采用共轭梯度法，Sridevi等^[5]采用随机搜索技术，Greco等^[3-4]采用蒙特卡罗法，Cheng等^[11]采用粒子群算法都对本例进行了求解。本文的计算结果见图6和表5。可见：由本文方法所得安全系数和以上研究者所得的都非常接近，但滑动面位置和形状有所区别。本文对滑动面形状未作严格的假定，滑面中后段微凸，与Greco^[3]的研究结果类似。而Cheng^[11]假定边坡的滑动面为上凹形，故与本文的结果略有不同。

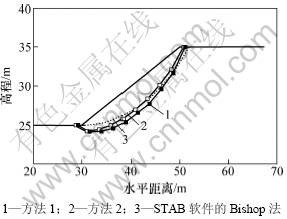
图4  算例1边坡剖面及计算结果

Fig.4  Slope section and computation results of example 1

表1  算例1计算结果对比

Table 1  Computation results of example 1

表2  算例2各土层物理力学参数

Table 2  Physico-mechanical parameters of different soil strata for example 2

图5  算例2边坡剖面及计算结果

Fig.5  Slope section and computation results of example 2

表3  算例2计算结果对比(简化Janbu法)

Table 3  Comparison of computation results for example 2(Simplified Janbu method)

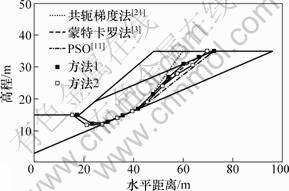
图6  算例3边坡剖面及计算结果

Fig.6  Slope section and computation results of example 3

表4  算例3各土层物理力学参数

Table 4  Physico-mechanical parameters of different soil strata for example 3

表5  算例3计算结果对比(简化Janbu法)

Table 5  Comparison of computation results for example 3(Simplified Janbu method)

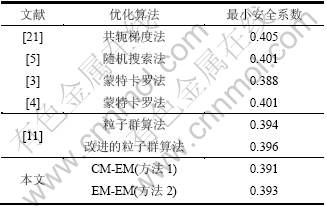
采用本文2种方法所得计算结果非常接近，方法1的精度略高于方法2的精度，但其迭代次数远远高于方法2的迭代次数，如表6所示(表6中NOFE1表示第2层搜索过程中调用第1层搜索算法的次数)。复合形法虽然计算精确，但收敛较慢，尤其在计算后期，很容易出现映射失败的现象。为加快复合形收敛，本文降低收敛精度，否则更加耗时。而第2层搜索的类电磁机制算法收敛较快。

采用程序计算时，也发现左、右交点位置对安全系数影响的敏感性远比滑动面其他节点的低，也证明了双层搜索方法的有效性。以算例3为例，将第2层搜索改成10次随机搜索，计算结果如图7和图8所示(图8中的安全系数按图7中滑动面右交点的横坐标从大到小排列)。图7中也存在类似于Arai 和Sridevi的滑动面，说明算例3中存在若干条滑动面，安全系数相差较小，滑面位置却不相同。需要指出的是：程序在搜索过程中，当产生的左、右交点与临界滑动面的节点相差较远时，相邻节点会成为交点，自动向内移动，如图9所示。所以，图7中的滑动面交点区域集中。

表6  方法1和方法2的计算迭代次数对比

Table 6  Computation results of methods 1 and 2

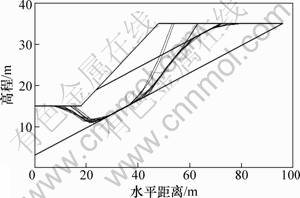
图7  10次随机搜索的滑动面位置

Fig.7  Location of critical failure surfaces obtained by 10 times random search

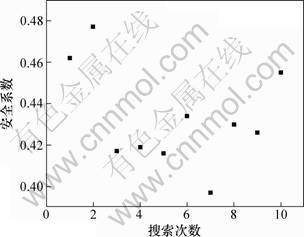
图8  10次随机搜索的安全系数

Fig.8  Factors of safety obtained by 10 times random search

类电磁机制算法的参数仅包括种群数目、局部搜索次数和全局搜索次数，参数设置的难度远远比其他智能优化算法的难度小。种群数目取20，全局搜索次数取100，就可完全满足边坡工程的计算要求。局部搜索使算法具有局部精细搜索的能力，其搜索次数对算法结果影响较小，取10次左右即可。类电磁机制算法的收敛很快，以算例2为例，方法2的计算收敛过程如图10所示，第1层搜索的类电磁机制算法经过50次迭代就可以基本保证收敛至满意解，本文取100次迭代是缘于保守考虑。一定次数的迭代中解没有改进也可视为算法停止，但是，这种方法对判断停止的参数很敏感，算法可能在收敛至全局最优值前就提前结束。

图9  滑动面修正示意图

Fig.9  Correction of slip surface

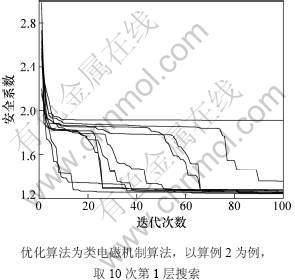
图10  第1层搜索的收敛情况

Fig.10  Process of convergence for first layer search

4  结论

(1) 类电磁机制算法是一种新型的群体智能优化算法，具有强大的全局搜索能力，同时算法还包含局部搜索，所以，该算法也具有精细局部搜索的能力。而且其参数设置难度低，收敛速度快。

(2) 本文结合双层搜索方法将类电磁机制算法应用于复杂边坡非圆弧滑动面的求解。将类电磁机制算法作为第1层搜索方法，将粒子数较少的类电磁机制算法或复合形法作为第2层搜索方法。

(3) 本文提出的方法可以准确、有效地确定复杂边坡非圆弧临界滑动面的位置。复合形法作为第2层搜索算法的计算精度比类电磁机制算法的高，但迭代次数成倍增加；左右交点位置对安全系数影响的敏感性比滑动面其他节点的低，也证明了双层搜索方法的有效性。

参考文献：

[1] Chen Z Y, Shao C M. Evaluation of minimum factor of safety in slope stability analysis[J]. Canadian Geotechnical Journal, 1983, 25(4): 735-748.

[2] Nguyen V U. Determination of critical slope failure surface[J]. Journal of Geotechnical Engineering, 1985, 111(2): 238-250.

[3] Greco V R. Efficient Monte Carlo technique for locating critical slip surface[J]. Journal of Geotechnical Engineering, 1996, 122(7): 517-525.

[4] Malkawi A I H, Hassan W F, Sarma S K. Global search method for locating general slip surface using Monte Carlo techniques[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(8): 688-698.

[5] Sridevi B, Deep K. Application of global optimization technique to slope stability analysis[C]//Proceeding of 6th International Symposium on Landslides. Christchurch, New Zealand, 1991, 573-578.

[6] Chen Z Y. Random trials used in determining global minimum factors of safety of slope[J]. Canadian Geotechnical Journal, 1992, 29: 225-233.

[7] Goh A T C. Search for critical slip circle using genetic algorithms[J]. Civil Engineering and Environmental Systems, 2000, 17(3): 181-211.

[8] Zolfaghari A R, Heath A C, McCombie P F. Simple genetic algorithm search for critical non-circular failure surface in slope stability analysis[J]. Computers and Geotechnics, 2005, 32: 139-152.

[9] 李守巨, 刘迎曦, 何翔, 等. 基于模拟退火算法的边坡最小安全系数全局搜索方法[J]. 岩石力学与工程学报, 2003, 22(2): 236-240.
LI Shou-ju, LIU Ying-xi, HE Xiang, et al. Global search algorithm of minimum safety factor for slope stability analysis based on annealing simulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 236-240.

[10] 陈云敏, 魏新江, 李育超. 边坡非圆弧临界滑动面的粒子群优化算法[J]. 岩石力学与工程学报, 2006, 25(7): 1443-1449.
CHEN Yun-min, WEI Xin-jiang, LI Yu-chao. Locating non-circular critical slip surfaces by partical swarm optimization algorithm[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(7): 1443-1449.

[11] Cheng Y M, Li L, Chi S C, et al. Particle swarm optimization algorithm for the location of the critical non-circular failure surface in two-dimensional slope stability analysis[J]. Computers and Geotechnics, 2007, 34(2): 92-103.

[12] Kahatadeniya K S, Nanakorn P, Neaupane K M. Determination of the critical failure surface for slope stability analysis using ant colony optimization[J]. Engineering Geology, 2009, 108(1/2): 133-141.

[13] Birbil S I. Stochastic global optimization techniques[D]. Raleigh: North Carolina State University. Department of Industrial Engineering, 2002: 22-42.

[14] Janbu N. Earth pressure and bearing capacity by generalized procedure of slices[C]//Glanviller W H ed. Proceedings of the 4th Int. Conf. of Soil Mechanics and Foundation Engineering. London: Butterworths Scientific Publications, 1957: 207-212.

[15] 潘家铮. 建筑物的抗滑稳定和滑坡分析[M]. 北京：水利出版社, 1980: 19.
PAN Jia-zheng. Analysis of building’s stability against sliding and landslide[M]. Beijing: China Water Conservancy Press, 1980: 19.

[16] 邹广电, 陈永平. 滑坡和边坡稳定性分析的模拟退火-随机搜索耦合算法[J]. 岩石力学与工程学报, 2004, 23(12): 2032-2037.
ZOU Guang-dian, CHEN Yong-ping. Coupling algorithm of simulated annealing algorithm and random search method for slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(12): 2032-2037.

[17] 施光燕, 董加礼. 最优化方法[M]. 北京: 高等教育出版社, 2005: 87-89.
SHI Guang-yan, DONG Jia-li. Methods of optimization[M]. Beijing: Higher Education Press, 2005: 87-89.

[18] Donald I B, Giam P. The ACADS slope stability programs review[J]. Proc 6th International Symposium on Landslides, 1992: 1665-1670.

[19] 陈祖煜. 土质边坡稳定分析: 原理·方法·程序[M]. 北京: 中国水利水电出版社, 2003: 370-371.
CHEN Zu-yu. Stability analysis of soil slopes-theory, methods and programs[M]. Beijing: China Water Power Press, 2003: 370-371.

[20] Bolton H P J, Heymann G, Groenwold A. Global search for critical failure surface in slope stability analysis[J]. Engineering Optimization, 2003(35): 51-65.

[21] Arai K, Tagyo K. Determination of noncircular slip surfaces giving the minimum factor of safety in slope stability analysis[J]. Soils and Foundations, 1985, 25(1): 43-51.

(编辑 陈灿华)

收稿日期：2010-11-15；修回日期：2011-03-01

基金项目：国家自然科学基金资助项目(10972238)；中南大学米塔尔学生创新项目(09MX14)；中南大学学位论文创新资助项目(2010ssxt237)

通信作者：曹平(1959-)，男，湖南祁东人，博士，教授，博士生导师，从事岩土工程理论、试验和数值计算的研究；电话：13973128263；E-mail：pcao_csu@tom.com