齿轮系统的KV和NSD接触力模型对比研究
吴丽娟，唐进元，陈思雨
(中南大学 机电工程学院，高性能复杂制造国家重点实验室，湖南 长沙，410083)
摘要：采用Kelvin-Voigt(KV)接触力模型和非线性弹簧-阻尼(NSD)接触力模型建立单自由度齿轮传动冲击动力学模型，模型考虑时变刚度和间隙。选取量纲一化的转速比为控制参数，转矩和冲击阻尼比系数为变化量，运用龙格-库塔数值分析方法，求解得到KV模型和NSD模型在相同参数条件下的相图和分岔响应曲线。在低速比条件下，动态响应基本相同；在高速比条件下，不同接触力模型条件下的响应存在差别。采用不同阻尼模型对系统低频响应影响不大，对高频响应的影响比较大，在NSD模型中，随着冲击阻尼系数的改变，共振区的响应会受到影响。
关键词：齿轮传动系统；接触力模型；冲击；非线性响应
中图分类号：TH113.1 文献标志码：A 文章编号：1672-7207(2014)05-1443-06
Comparative study of Kelvin-Voigt and nonlinear spring and damping contact force models of gear system
WU Lijuan, TANG Jinyuan, CHEN Siyu
(State Key Laboratory of High Performance and Complex Manufacturing,
School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
Abstract: The single-degree-of-freedom gear dynamic transmission system with time-varying stiffness and backlash was established adopting two different contact force models, Kelvin-Voigt (KV) contact force model and nonlinear spring and damping (NSD) contact force model. The dimensionless velocity was regarded as the controlling parameter, the Runge-Kutta numerical integration of the differential equations was carried out at different torque values and impact damping ratio conditions. The bifurcation graphs and phase graphs were deduced. At low frequency, the dynamic responses are similar. However, the dynamic responses are different at high frequency. The dynamic responses are affected with the increase of impact damping ratio in the Nonlinear spring and damping contact force model.
Key words: gear system; contact force model; impact; nonlinear dynamic responses
齿轮传动系统中，安装误差、制造误差、间隙等因素导致传动装置产生碰撞和冲击，影响齿轮传动系统的动态性能和传动精度，因此，对含间隙和冲击碰撞系统机理的研究具有重要意义。齿轮动力学研究中，接触力模型的选择对动力学建模与分析十分关键[1]。2个弹性体接触力模型建立主要有以下4种方法：恢复系数法[2]、圣维南法[3]、非线性有限元法和弹簧-阻尼模型方法[4-5]，恢复系数法和弹簧-阻尼模型方法在各种涉及接触的动力学问题研究中被广泛运用。在弹簧-阻尼的连续接触模型中，假定碰撞阶段是碰撞力连续作用的过程，碰撞面之间由弹簧和阻尼连接，直接将碰撞力引入到动力学模型中，较真实地描述了碰撞过程。弹簧-阻尼接触力模型，主要有Kelvin-Voigt 模型(KV)，Hertz’s模型(HS)，非线性弹簧-阻尼模型(NSD)。KV模型[6]考虑接触过程中的弹性变形和能量耗散，采用线性接触刚度和阻尼。陈思雨等[7]对该弹性接触力模型进行了相关研究。但是，Hertz’s模型只考虑弹性变形而未考虑阻尼，恢复系数取1。Hertz’s模型描述的是纯弹性接触过程，在接触的过程中不存在能量的损耗。Dubowsky等[8]认为轮齿间的接触力是与相对变形和冲击速度相关的非线性函数。在Hertz’s 模型的基础上，Hunt等[9]提出考虑非线性阻尼项的弹簧-阻尼模型(NSD)。已有研究表明：材料阻尼系数非常小时，KV模型能较好地描述单自由度黏弹性碰撞系统的动力学响应，但是该模型中的碰撞力模型没能准确描述接触过程中的能量转换[10]，从而引入迟滞阻尼项，得到NSD模型，并得到广泛应用[11]。Machado等[12]综述了基于Hertz’s基础理论建立的各种接触力模型动力学响应之间的差别。Ajibose等[5]对比分析了多体动力学系统中采用这3种不同接触力模型的系统响应。在齿轮动力学研究方面，Azar等[13]将非线性迟滞阻尼模型引入到齿轮传动系统的冲击动力学响应研究中，对比分析了数值仿真和试验结果，输出轴试验结果证明了数值模拟的正确性。Kim等[14]也将非线性迟滞阻尼引入到齿轮传动系统动力学模型，采用谐波平衡法和数值分析法研究系统含有间隙和不包含间隙情况下，得到系统的频谱特性曲线以及系统出现次谐和超谐响应的规律。本文作者试图建立含间隙的单自由度齿轮传动动力学模型，分别采用KV模型和NSD模型，对比研究不同模型条件下的幅频响应特性、以及系统出现倍周期分岔和混沌的规律，分析采用NSD冲击模型时在不同冲击阻尼系数条件下的系统响应。
1 齿轮传动动力学模型
本文构建的齿轮传动物理模型如图1所示。其中：Ip和Ig分别表示主动轮和从动轮的转动惯量；Rp和Rg分别为主动轮和从动轮的基圆半径；Tp和Tg分别为主动轮和从动轮的转矩；θp和θg分别为主动轮和从动轮的角位移。
由于间隙的存在，将主动轮和从动轮之间的相对位移分为3种情况来讨论，分别是齿面冲击，无接触冲击状态和齿背冲击。间隙函数可表示为
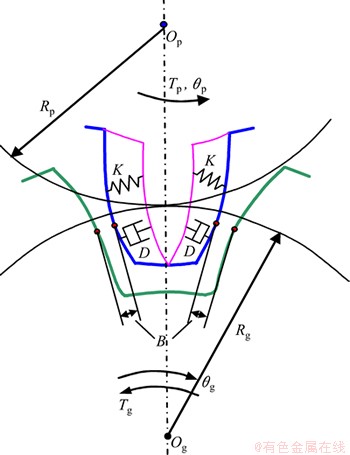
图1 轮齿传动物理模型
Fig. 1 Physical model of gear transmission system
其中：定义动态传递误差
，引入静态传递误差e(t)，因此，沿啮合线方向的相对位移
，b表示轮齿间最大间隙值的1/2。
根据上述定义，结合KV接触力模型，可得到单自由度齿轮传动系统的接触-碰撞动力学方程为
其中：cm为轮齿间的材料阻尼系数；k(t)为轮齿间的啮合刚度。
轮齿冲击力简单地用黏性阻尼表示，不能真实地反映轮齿冲击特性。根据Hunt等[9]提出的考虑非线性迟滞阻尼，建立NSD系统动力学模型，系统动力学方程为
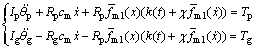
其中：迟滞阻尼系数
；
为冲击运动时冲击点的速度。
在齿轮传动系统中，轮齿啮合刚度k(t)和静态传递误差e(t)均为周期变化函数，可用Fouriers级数表 示为：
，
，
，
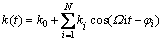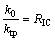其中：k0为平均啮合刚度；ki为谐波分量幅；ktp为单齿啮合刚度；
为初始相位；
为齿轮传动系统的转速，RIC为重合度；e0为静态激励的平均值；ei为激励的谐波分量幅值。
由于式为半静定方程组，同时为更方便地进行求解，引入等效集中质量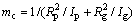
，外作用力
，并令
，
，
，
，
，
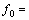
。为不失一般性，方程中的
和
仍用x和t表示。因此，式进行量纲一化处理后，可得
同理，对式进行量纲一化处理后，可得
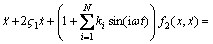
函数f1和f2可以写成
其中：
为迟滞阻尼系数比。
2 不同激励条件下的齿轮传动非线性动力学响应特性
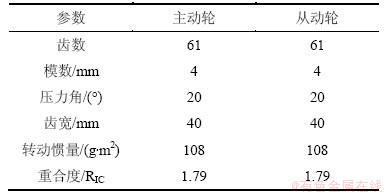
主动轮与从动轮的几何参数设置如表1所示。
表1 齿轮系统几何参数
Table 1 Geometric parameters of gear system
在图1 所示的物理模型中，取间隙2b=7.34×10-4 m；材料阻尼比
=0.05；迟滞阻尼比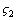
=0.02；傅里叶级数N=1，M=1；外载荷Tp=500 N·m；外激励f1=0.2；初始相位
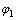=0。在没有特殊说明的情况下，系统参数的值不变，取频率
为控制参数。
2.1 载荷和转速对不同接触力模型的影响
图2所示为Tp=1 000 N·m，f1=0.2，ω=[0.2, 1]时齿轮传动系统相对速度分岔图。图3所示为Tp=500 N·m，f1=0.2, ω=[0.2, 1.2]时齿轮传动系统相对速度分岔图。图4所示为Tp=500 N·m，f1=0.2, [0.85, 1]时齿轮传动系统相对速度分岔图。图5所示为Tp=100 N·m，f1=0.2，ω=[0.2, 1.2]时齿轮传动系统相对速度分岔图。KV模型和NSD模型的系统响应结果如图2~4所示。从图2~4可见：随着转矩的减小，轮齿冲击系统在低频区域更容易进入混沌状态。在Tp=1 000 N·m和Tp=100 N·m条件下，KV模型和NSD模型的非线性动力学响应几乎相同。在Tp=1 000 N·m条件下，ω=[0.2, 1.0]的区间内系统不出现混沌现象，在Tp=100 N·m载荷条件下，系统中多次出现由周期解经过阵发性路径进入混沌运动。当Tp=500 N·m时，在低频区，KV模型的响应与NSD模型的响应基本相同，倍周期分岔点出现的频率有较小差异。在高频区，KV冲击动力学模型和NSD冲击动力学模型的周期性窗口的大小存在差异，分别为ω=[0.87, 0.89]和ω=[0.86, 0.91]。在周期性窗口的频率区间内，都存在周期解发生倍分岔从而出现弱混沌现象，继而退化成周期运动，在某转速条件下由阵发性路径进入混沌运动。在Tp=100 N·m条件下，系统出现多处分岔和混沌，系统非常复杂，KV模型和NSD模型的差异性不明显。
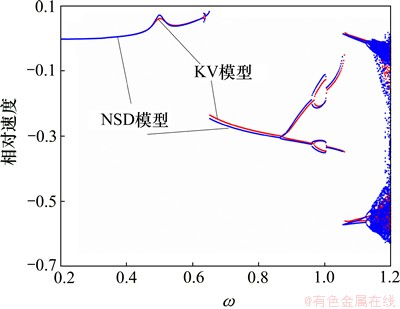
图2 Tp=1 000 N·m，f1=0.2，ω=[0.2, 1]时齿轮传动系统相对速度分岔图
Fig. 2 Bifurcation diagrams of relative velocity of gear system at Tp=1 000 N·m，f1=0.2，ω=[0.2, 1]
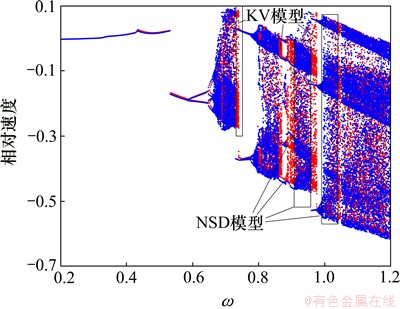
图3 Tp=500 N·m，f1=0.2, ω=[0.2, 1.2]时齿轮传动系统相对速度分岔图
Fig. 3 Bifurcation diagrams of relative velocity of gear system at Tp=500 N·m，f1=0.2, ω=[0.2, 1.2]
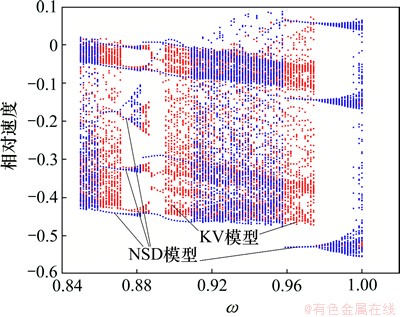
图4 Tp=500 N·m，f1=0.2, [0.85, 1]时齿轮传动系统相对速度分岔图
Fig. 4 Bifurcation diagrams of relative velocity of gear system at Tp=500 N·m，f1=0.2, ω=[0.85, 1]
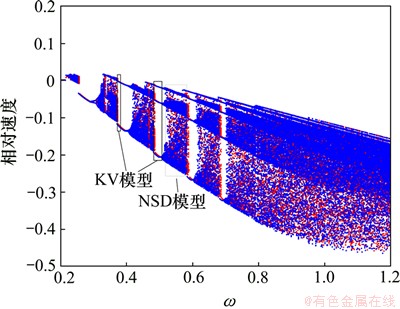
图5 Tp=100 N·m，f1=0.2，ω=[0.2, 1.2]时齿轮传动系统相对速度分岔图
Fig. 5 Bifurcation diagrams of relative velocity of gear system at Tp=100 N·m，f1=0.2，ω=[0.2, 1.2]
系统中的固有转速ωn=2 482 r/min，在ω=0.2和ω=0.875时系统的实际转速分别为Ω=496 r/min和Ω= 2 172 r/min。图6所示为Tp=500 N·m，f1=0.2, ω=0.2时不同的转速条件下时齿轮传动系统的相图。图7所示为Tp=500 N·m，f1=0.2, ω=0.875时不同的转速条件下时齿轮传动系统的相图。从图6和7可见：在低速条件下，冲击力模型的选择对系统响应的影响很小。在高速条件下，KV模型中出现混沌响应，在NSD模型出现的是多周期解运动。
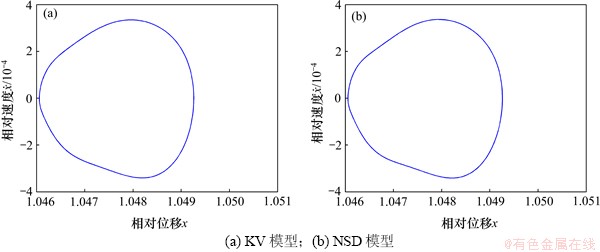
图6 Tp=500 N·m，f1=0.2, ω=0.2时不同的转速条件下时齿轮传动系统的相图
Fig. 6 Phase graphs of gear system with different velocity conditions at Tp=500 N·m，f1=0.2, ω=0.2
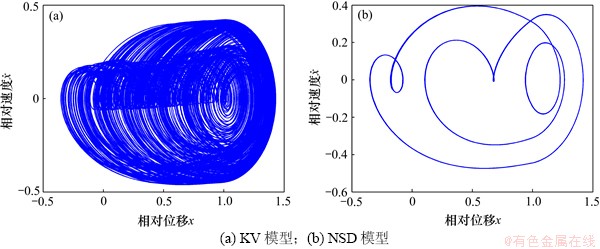
图7 Tp=500 N·m，f1=0.2, ω=0.875时不同的转速条件下时齿轮传动系统的相图
Fig. 7 Phase graphs of gear system with different velocity conditions at Tp=500 N·m，f1=0.2, ω=0.875
2.2 不同冲击阻尼系数对NSD模型的动力学响应的影响
图8所示为Tp=1 000 N·m，f1=0.2，ω=[0.2, 1.2]，
2=[0.02, 0.015, 0.01]时NSD模型条件下齿轮传动系统相对速度分岔图。图9所示为Tp=500 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]时NSD模型条件下齿轮传动系统相对速度分岔图。图10所示为Tp=100 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]时NSD模型条件下齿轮传动系统相对速度分岔图。从图8~10可见：在不同的冲击阻尼系数条件下，系统的周期响应、分岔和混沌仅发生细微的变化。在Tp=1 000 N·m和Tp=100 N·m条件下，系统响应不受冲击阻尼系数的变化的影响，在Tp=500 N·m条件下，系统的共振区的响应会受到影响。随着阻尼系数的降低，系统更加容易进入混沌状态。在轻载条件下，不同阻尼参数条件下的系统的响应之间基本相同。
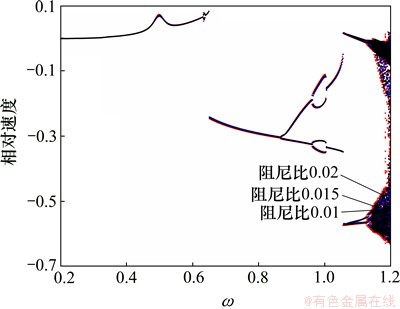
图8 Tp=1 000 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]时NSD模型条件下齿轮传动系统相对速度分岔图
Fig. 8 Bifurcation diagrams of relative velocity of gear system with NSD contact force model at Tp=1 000 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]
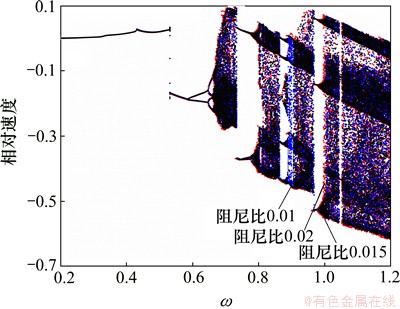
图9 Tp=500 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]时NSD模型条件下齿轮传动系统相对速度分岔图
Fig. 9 Bifurcation diagrams of relative velocity of gear system with NSD contact force model at Tp=500 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]
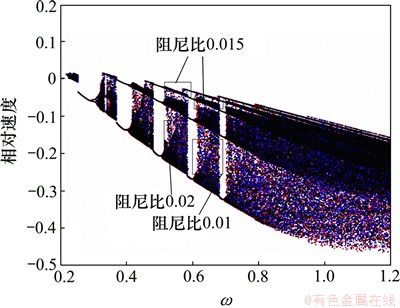
图10 Tp=100 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]时NSD模型条件下齿轮传动系统相对速度分岔图
Fig. 10 Bifurcation diagrams of relative velocity of gear system with NSD contact force model at Tp=100 N·m，f1=0.2，ω=[0.2, 1.2]，2=[0.02, 0.015, 0.01]
3 结论
(1) 给出齿轮传动KV接触力模型与NSD接触力模型的非线性动力学响应的比较结果。
(2) KV接触力模型与NSD接触力模型的非线性动力学响应的差异性与载荷紧密相关。
(3) 在低速条件下，2种接触力模型的动力学响应不存在差异性。在高速条件下，KV模型的周期性窗口比NSD模型的周期性窗口小。
(4) 在NSD中，冲击阻尼系数直接影响系统非线性的响应，接触力模型中的冲击阻尼系数选取十分重要，工程实际中应该通过材料性能实验确定相应的冲击阻尼系数。
参考文献：
[1] Vedmar L, Andersson A. A method to determine dynamic loads on spur gear teeth and on bearings[J]. Journal of Sound and Vibration, 2003, 267(10): 1065-1084.
[2] 罗冠炜, 谢建华. 两自由度塑性碰撞振动系统的动力学研究[J]. 力学学报, 2000, 32(5): 579-586.
LUO Guanwei, XIE Jianhua. Dynamics of a two-degree-of- freedom vibration system with perfectly plastic impacts[J]. Acta Mechanica Sinica, 2000, 32(5): 579-586.
[3] 丁遂亮, 洪嘉振. 柔性多体系统接触碰撞动力学研究[J]. 上海交通大学学报, 2003, 28(12): 75-78.
DING Suiliang, HONG Jiazhen. Dynamic analysis of impact loads in flexible multibody systems by FEM[J]. Journal of Shanghai Jiaotong University, 2003, 28(12): 75-78.
[4] Tang J Y, Wang Q B, Wu L J, et al. Bifurcation analysis of impact model in gear transmission system[J]. Applied Mechanics and Materials, 2011, 86(11): 479-482.
[5] Ajibose O K, Wiercigroch M, Pavlovskaia E, et al. Contact force models and dynamics of a drifting oscillator[C]// ASME Conference Proceedings. San Diego. USA: ASME, 2009: 1387-1394.
[6] Goldsmith W. Impact: The theory and physical behaviour of colliding solids[M]. London, England, Edward Arnold Ltd., 2001: 1-379.
[7] 陈思雨, 唐进元. 间隙对含摩擦和时变刚度的齿轮系统动力学响应的影响[J]. 机械工程学报, 2009, 45(8): 119-124.
CHEN Siyu, TANG Jinyuan. Effect of backlash on dynamics of spur gear pair system with friction and time-varying stiffness[J]. Journal of Mechanical Engineering, 2009, 45(8): 119-124.
[8] Dubowsky J S F D, Costello H. The dynamic modeling of flexible spatial machine systems with clearance connections[J]. Journal of Mechanisms, Transmissions and Automation in Design, 1987, 109(7): 87-94.
[9] Hunt K H, Crossley F R E. Coefficient of restitution interpreted as damping in vibroimpact[J]. Journal of Applied Mechanics, 1975, 42(5): 440-445.
[10] Gilardi G, Sharf I. Literature survey of contact dynamics modelling[J]. Mechanism and Machine Theory, 2002, 37(10): 1213-1239.
[11] Silva P C, Martins J M. Evaluation of the contact forces developed in the lower limb/orthosis interface for comfort design[J]. Multibody System Dynamics,2010, 24(9): 367-388.
[12] Machado M, Moreira P, Flores P, et al. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory[J]. Mechanism and Machine Theory, 2012, 53(7): 99-121.
[13] Azar R C, Crossley F R E. Digital simulation of impact phenomenon in spur gear systems[J]. Journal of Engineering for Industry, 1977, 99(8): 792-798.
[14] Kim T C, Rook T E. Effect of nonlinear impact damping on the frequency response of a torsional system with clearance[J]. Journal of Sound and Vibration,2005, 281(3/4/5): 995-1021.
(编辑 邓履翔)
收稿日期：2013-06-09；修回日期：2013-08-08
基金项目：国家自然科学基金资助项目(51275530)；国家重点基础研究发展规划(“973”计划)项目(2011CB706800)；研究生自主探索创新基金资助项目(2013zzts198)
通信作者：唐进元(1962-)，男，湖南永州人，教授，从事齿轮加工和动力学研究；电话：0731-88876350；E-mail: jytangcsu@163.com
