垂直轴风力机主动式变桨距控制规律

张立勋，梁迎彬，尉越啸，李二肖，杨勇

(哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨，150001)

摘要：针对定桨距垂直轴风力机启动能力差与风能利用率较低的问题，对主动式变桨距控制方法和规律进行研究，以达到提高风能利用率的目的。以双盘面多流管理论为基础，分析叶片的局部流场，建立风力机的数学模型，并以最大瞬时功率为目标函数设计桨距角优化程序，通过分析获得不同尖速比下的桨距角控制规律。根据CFD模型，对定桨距风力机进行数值模拟，分析不同桨距角下的气动性能；对优化后的控制规律在CFD中进行仿真研究，分析风力机的力学行为和风能利用率。研究结果表明：外偏置桨距角可以提高上盘面的气动性能且在桨距角为-4°时获得最大的风能利用率；变桨距控制下的有效力矩区相比定桨距风力机增加了1倍，最大风能利用率也高达39.12%，主动式变桨距控制规律可以明显提高风力机的整体性能。

关键词：垂直轴风力机；主动式；变桨距；风能利用率；CFD

中图分类号：TK89          文献标志码：A         文章编号：1672-7207(2013)06-2561-08

Active variable-pitch control laws for vertical axis wind turbine

ZHANG Lixun, LIANG Yingbin, WEI Yuexiao, LI Erxiao, YANG Yong

(College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract: Aiming at the poor self-starting and low power coefficient of fixed pitch vertical axis wind turbine (VAWT), investigations on method and control laws of active variable-pitch technology were conducted to improve power coefficient. Based on double-multiple streamtube models, studies of local flow field around blades were carried out, and mathematical model of VAWT was built; then an optimization procedure for computing the optimal pitch angle was proposed, the target function of which was based on maximum instantaneous power output, thus the control laws of pitch angle under various tip speed ratios were obtained. Numerical simulations of fixed pitch VAWT were carried out based on the CFD model to analyze aerodynamic performance under different pitch angles; meanwhile, researches were initiated by the method of CFD simulation, and the control laws of active variable-pitch obtained by the procedure were used, then the forces around the rotor and power coefficient under the operating conditions were obtained. The results show that VAWT with out-offset pitch angle has a better aerodynamic behavior at upstream and the maximum power coefficient is obtained at about -4°. Compared with fixed pitch VAWT, self-starting performance and power coefficient of VAWT under the control of the active variable-pitch control laws are greatly improved, while the effective region with high torque is nearly twice of that of fixed pitch VAWT and power coefficient is as high as 39.12%.

Key words: vertical axis wind turbine; active; variable-pitch; power coefficient; CFD

在能源危机和低碳经济快速发展的趋势下，新能源的开发与利用倍受国内外学者重视^[1-2]。风能作为清洁可再生能源，已成为最具潜力的替代能源之一。随着研究的深入以及风力发电技术的不断发展，垂直轴风力机凭借噪音小、安装维护方便以及翼型制造容易等优势^[2-4]，成为关注的焦点，并具有了与水平轴风力机相媲美的潜力^[5-6]。然而，垂直轴风力机启动性能差甚至无法自启动，以及风能利用率相比水平轴风力机较低等问题，极大限制了垂直轴风力机的发展和推广。

研究表明，变桨距技术是解决垂直轴风力机存在问题的有效方法。Pryor^[7]发明了一种应用W型机构的垂直轴风力机变桨距方法，Pawsey^[8]设计了一款基于气动力与惯性力原理的离心锤式变桨距垂直轴风力机。Dress^[9]研制了“Cycloturbine”风力机，采用凸轮机构实现了变桨距控制，通过理论分析发现该类风力机的最大风能利用率可达0.45^[10]。张亮等^[11-12]研究了桨距角对水轮机性能的影响。张松等^[13]则设计了一款同步变桨距垂直轴风力机，由1台伺服电机实现多组叶片的变桨距控制，样机在尖速比0.6附近获得最大风能利用率。等^[14]研究了一种基于正弦规律的变桨距水轮机，该水轮机在尖速比3附近获得最大发电效率，约为38%。Hwang等^[15]提出了具有摆线规律的可独立变桨距控制的水轮机，变桨距控制下的性能相比定桨距水轮机有70%的提高。虽然变桨距垂直轴风力机已经得到初步发展，但变桨距控制规律却一直处于实验室阶段。本文作者针对风力机变桨距控制规律展开深入研究，以最大瞬时功率为目标函数设计桨距角优化程序，并在CFD中对设计的变桨距规律进行验证，分析变桨距控制下风力机的气动性能。

1  变桨距垂直轴风力机数学模型

为了获得变桨距控制规律，需要以叶片的气动载荷和风力机的气动性能为基础建立风力机的数学模型，分析桨距角与风能利用率的关系。由于流管理论可以有效地预测风力机的整体性能，是一种很好的辅助风力机设计的模型，故采用双盘面多流管理论研究风力机的性能。

1.1  双盘面多流管模型

双盘面多流管模型由Paraschivoiu提出^[16]，其在流管理论的基础上又将每个流管分割为上、下2个盘面，可以实现上、下2个盘面的不同性能分析，如图1所示。

依据流管理论，风力机局部风速为：

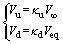                (1)

式中：V_∞为无穷远处来流风速；V_u和V_d分别为上、下盘面局部风速；κ_u和κ_d分别为上、下盘面速度因子。

现定义变量κ_θ为垂直轴风力机0°~360°范围内的速度因子，式(1)可以简化为：

                  (2)

其中：当叶片位于上盘面时κ_θ=κ_u；当叶片位于下盘面时κ_θ=κ_d(2κ_u-1)。

垂直轴风力机的相对速度W与局部风速V_θ的关系如图2所示。

W=V_θ+U                  (3)

        (4)

式中：U为风力机切向速度，且U=ω×R。

风力机局部尖速比λ_θ可以表示为：

                 (5)

图1  双盘面多流管模型

Fig. 1  Double-multiple streamtube model

图2  叶片局部流场与气动力分析

Fig. 2  Analysis of local flow field around blade and aerodynamic forces acting on blade

由图2可知风力机的来流角γ为

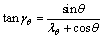            (6)

根据动量理论，单流管内的轴向力为

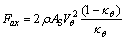           (7)

其中：ρ为空气密度；A_S为流管面积。

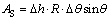            (8)

基于叶素理论，单流管内作用在叶片上的气动力为

 (9)

则联立式(7)和(9)，采用数值解法即可得到风力机的速度因子。

1.2  变桨距垂直轴风力机数学模型

为分析叶片桨距角与风能利用率的关系，建立了叶片的气弹动力学模型，如图3所示。作用在叶片上的气动载荷简化为力矢量F_A和相对于简化中心A的力偶M_A，点P和点G分别为叶片的转动中心和重心。如图3所示，升力F_l与阻力F_d的关系为

            (10)

并定义垂直轴风力机的切向力系数C_τ为

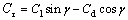           (11)

式中：C_l为升力系数；C_d为阻力系数。

图3  叶片的气弹动力学模型

Fig. 3  Aeroelastic dynamic model of blade

值得注意的是：简化中心A随方位角θ变化而变化，并记作r_A。由简化中心位置变化导致的额外气动力矩会影响叶片桨距角，进而影响风力机的气动性能，严重时会导致叶片颤振。因此，有必要分析作用在叶片转轴处的俯仰力矩，即

         (12)

由式(12)可知：叶片转轴处的俯仰力矩会对叶片桨距角产生影响，这样就会引入额外的桨距角β_ex，

                (13)

其中：K_α为叶片转动中心的刚度。

则叶片实际的桨距角β_a为

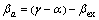             (14)

单叶片产生的瞬时力矩M_θ为

            (15)

单叶片的力矩系数C_m为：

              (16)

则变桨距垂直轴风力机的瞬时功率P_θ为

               (17)

式中：N为叶片数量；M_θi为第i个叶片产生的瞬时力矩，且i=1，2，…，N。

变桨距垂直轴风力机的风能利用率C_p可以表示为

               (18)

由式(15)和式(17)可知：垂直轴风力机的瞬时功率是关于升力系数，阻力系数以及局部尖速比λ_θ的函数，而叶片桨距角直接决定了叶片的气动性能，故可通过改变桨距角方法以实现最大功率输出，提高垂直轴风力机的风能利用率。

2  CFD模型及气动特性分析

为了获得不同尖速比下的桨距角变化规律，先对定桨距垂直轴风力机进行CFD仿真研究，分析不同桨距角(对于定桨距垂直轴风力机即为安装角)下的气动性能以及桨距角与风能利用率的关系，进而得到桨距角变化趋势。

2.1  CFD模型

对于直叶片垂直轴风力机，在不考虑叶片端部湍流或者叶片无限长的情况下，翼型周围的流场很相似，可以将三维流场简化为二维流场^[17]。根据质量守恒，动量守恒以及连续性理论建立流场模型，采用二维不可压缩N-S方程作为控制方程，并对流体方程进行了RANS雷诺平均处理，即瞬时速度u_i和压力p分别为各自时均值和脉动值的和。在笛卡儿坐标系下流体方程表示为

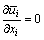                 (19)

  (20)

式中：项为雷诺应力，并将速度脉动的二阶关联量表示成平均速度梯度与湍流黏性系数的乘积，即

  (21)

式中：μ_t和k分别为动态粘涡系数和湍流动能。

由Howell等^[18]的研究发现，重整化群的k-ε模型修正了耗散率方程，保证风力机的数值模拟有较高的精度，故采用k-ε RNG模型，即

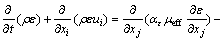
由于k-ε RNG模型可使得流体方程封闭，有效解决了高雷诺数问题，而低雷诺数问题则采用壁面函数法处理。同时采用压力-速度耦合以及标准壁面方程的方法，研究大攻角下流场的分离情况。本文建立了4叶片垂直轴风力机的CFD模型，风轮半径为2 m，叶片展长为2 m，采用NACA0015对称翼型，弦长为400 mm，来流风速为10 m/s，并采用速度进口、压力出口和无滑移壁面等边界条件。

2.2  翼型气动性能分析

由式(17)可知：翼型的气动参数决定了风力机的最大瞬时功率，获得翼型的气动参数很重要。对NACA0015翼型进行CFD仿真研究，获得了翼型的静态升阻力系数，如图4所示。

由图4可知：随着弦长的增加，升力系数C_l增加，阻力系数C_d下降，翼型的升阻比变大，有助于风能利用率的提高；随着弦长C的增加，阻力系数曲线右移，表明翼型的静态失速角增加，削弱了翼型边界层的分离；当翼型失速后，压差阻力相比摩擦阻力起主导作用，阻力系数急剧上升；对于升力系数，失速前升力系数随有效攻角变大而变大，失速后升力系数快速下降；最大升力系数随弦长增大而增大。

图4  NACA0015翼型的升力和阻力系数

Fig. 4  Lift and drag coefficients of NACA0015

经CFD研究还得到了不同攻角下翼型的压力分布，如图5所示。由图5可知：翼型前缘附近的负压梯度对升力的形成贡献很大；在低压区形成吸力使翼型绕叶片转轴从高压区转向低压区，即负压形成了负升力。这表明与负升力对应的有效攻角为负值。

图5  NACA0015翼型的压力分布系数

Fig. 5  Pressure coefficient distribution of NACA0015

2.3  定桨距垂直轴风力机气动特性分析

在获得翼型的气动性能之后，还需研究叶片桨距角与风能利用率的关系，以便规划变桨距控制规律。由于尖速比决定了风力机的运转特性，直接影响风能的利用，所以，研究风速与尖速比的对应关系也很重要。经CFD仿真研究，得到不同风速下尖速比与风能利用率的关系，如图6所示。

图6  不同风速下尖速比与风能利用率的关系

Fig. 6  Relationship between power coefficient and tip speed ratio under various wind speeds

由图6可知：随着风速的增大，风能利用率的峰也增大，且风能利用率峰值所对应的尖速比也增加，说明高尖速比下的风能利用率较高，且风力机尖速比在2.5~3.5范围内具有较高的风能利用率。此外，在尖速比小于2的情况下，风力机启动后的风能利用率差别不大，垂直轴风力机在尖速比λ＜2.5的区间内的气动性能有待改善。

固定垂直轴风力机叶片桨距角进行CFD仿真，通过改变桨距角得到了桨距角与风力机性能的关系曲线，如图7所示。由图7可以看出：桨距角为-4°时的风能利用率最高，并且具有较宽的有效工作范围。经分析可知桨距角-4°是定桨距风力机性能的转折点，风能利用率呈现先增加后下降的趋势；当桨距角由2°向-4°变化时，风能利用率峰值朝低尖速比方向移动，且对应的最大风能利用率提高。由此可知：外偏置桨距角可以增大风能利用率的峰值和有效作用范围。

现对桨距角进行如下解释：垂直轴风力机的运行轨迹为圆，若翼型前缘位于圆内则定义为内偏置桨距角，且为正值；若翼型前缘恰在圆上，则桨距角为0°；否则为外偏置桨距角，且为负值。图8所示为定桨距垂直轴风力机在不同桨距角下的力矩系数。

由图8可知：上盘面相比下盘面的力矩系数较大。这是因为在上盘面大部分风能转化为机械能，下盘面风速几乎是上盘面风速的一半，加之风能与风速的三次方呈正比，所以，下盘面的力矩系数很小。从图8还可以看出：当桨距角为正值时，风力机在较小的方位角就进入有效力矩作用范围，也最先退出有效力矩作用区；当桨距角为负值时，相比正值桨距角较晚进入有效力矩作用范围，且随着桨距角幅值的增大，相应的方位角也增大。

图7  定桨距垂直轴风机叶片桨距角与风能利用率的关系

Fig. 7  Relationship between pitch angle and power coefficient of fixed pitch vertical axis wind turbine

图8  定桨距垂直轴风力机叶片桨距角与力矩系数的关系

Fig. 8  Relationship between pitch angle and torque coefficient of fixed pitch vertical axis wind turbine

由图8可知：桨距角为-4°时力矩系数较高且有效力矩作用区较宽，具有较好的气动性能；当桨距角为正值时，风力机进入有效力矩作用区时的力矩系数基本一致；当桨距角为负值时，风力机退出有效力矩作用区时的力矩系数差别也较小。由此可得出：设置内偏置桨距角或者小幅值的外偏置桨距角，使风力机在小方位角进入有效力矩作用区；且设置外偏置桨距角使风力机延缓退出有效力矩作用区，通过该方法可以实现风力机气动性能的提高。

3  变桨距控制规律及仿真分析

3.1  以最大瞬时功率为目标函数的变桨距控制规律

图9所示为确定垂直轴风力机桨距角变化规律的程序框图。其原理为：根据结构参数、流场和运行条件以及气动参数求解速度因子；在考虑局部风速和局部尖速比的情况下，根据式(17)建立风力机瞬时功率；对初始气动参数进行修正，求解瞬时功率最大值及对应的桨距角，最终得到风力机0°~360°范围内的桨距角控制规律。应用MATLAB软件编写优化程序，获得不同尖速比下桨距角变化规律，如图10所示。

图9  确定桨距角控制规律的程序框图

Fig. 9  Program diagram to obtain control rule of pitch angle

图10所示为不同尖速比下的桨距角控制规律。图10中曲线关于180°中心对称，与风力机流场特性基本吻合；随着尖速比的增加，桨距角变化量减小，表明高尖速比下是否采用变桨距控制还需全局衡量。

3.2  变桨距控制规律仿真分析

由式(11)可知：切向力系数在一定程度上可以反映风力机性能，经CFD仿真得到了定桨距和变桨距风力机切向力系数，如图11所示。

由图11可以看出：无论是定桨距还是变桨距风力机，都在上盘面取得切向力系数的峰值，而下盘面的切向力系数很小。这是因为在上盘面流体不会或很少发生分离，湍流损失较少，大部分气动力转化为升力；而下盘面流体速度较低，或因忽略下盘面流线方向变化以及尾涡影响，致使下盘面的切向力系数较小。此外，与定桨距垂直轴风力机相比，在变桨距控制下风力机在方位角90°~180°范围内的性能得到了改善，风力机切向力有效作用范围约占风力机整周的1/2，而定桨距垂直轴风力机却只占有1/4圆周。结果表明该主动式变桨距控制规律显著提高了垂直轴风力机的整体性能。

图10  以最大瞬时功率为目标函数的变桨距控制规律

Fig. 10  Active variable-pitch control laws obtained by objective function of maximum instantaneous power

图11  变桨距与定桨距垂直轴风力机切向力系数对比分析

Fig. 11  Comparison of tangential force coefficient between fixed pitch and variable-pitch vertical axis wind turbine

另外，经CFD仿真还得了作用在叶片上的俯仰力矩，在变桨距控制下叶片的俯仰力矩与定桨距风力机的对比结果，如图12所示。

由图12可知：定桨距垂直轴风力机上盘面俯仰力矩变化剧烈，而在变桨距控制下作用在叶片上的俯仰力矩变化比较平缓。这是因为变桨距控制提高了叶片的动态失速角，有效地抑制了动态失速现象的发生，而且叶片桨距角的动态调节降低了压力梯度。在变桨距控制下，作用在叶片上的俯仰力矩大部分是负值，且与叶片运动方向一致，对垂直轴风力机的变桨距控制有利，可以降低由伺服电动机在主动变桨距控制下功率消耗；而作用在定桨距垂直轴风力机上的俯仰力矩是必须要克服的阻力矩。

图12  变桨距与定桨距控制下叶片俯仰力矩对比分析

Fig. 12  Comparison of torque acting on blade between fixed pitch and variable-pitch vertical axis wind turbine

图13所示为作用在风力机上的合力矩系数。从图13可见：与定桨距垂直轴风力机相比，变桨距控制下的合力矩系数较大，并且力矩系数波动较小，表明变桨距控制可以提供更加稳定的功率输出；叶片在相同方位角下具有一致的运动规律，且呈周期性变化，说明合力矩系数只与方位角有关，与具体哪个叶片起作用无关。

图13  变桨距与定桨距垂直轴风力机合力矩系数对比分析

Fig. 13  Comparison of total torque coefficient between fixed pitch and variable-pitch vertical axis wind turbine

图14所示为变桨距控制下垂直轴风力机的风能利用率。由图14可知：随着尖速比的增大风能利用率提高，且在尖速比为2.6附近取得峰值。主动式变桨距控制极大地提高了尖速比λ＜2.6区间下的风能利用率。在尖速比λ=2，风速为10 m/s的情况下，在变桨距规律控制下垂直轴风力机的风能利用率达到39.12%，而定桨距风力机(β=0°)的风能利用率只有19.80%，风力机利用率提高近2倍。对于定桨距垂直轴风力机，桨距角为-4°时具有较高的风能利用率，但也远远低于变桨距风力机的风能利用率。

图14  变桨距控制下垂直轴风力机的风能利用率 (V_∞=10 m/s)

Fig. 14  Power coefficient of vertical axis wind turbine with active variable-pitch control at V_∞=10 m/s

4  结论

(1) 通过对定桨距垂直轴风力机的数值模拟发现，外偏置桨距角可以改善风力机上盘面的气动性能，且在桨距角为-4°时获得最大风能利用率。

(2) 在主动式变桨距控制下风力机的有效切向力作用范围占风轮整周的1/2，而定桨距只占圆周的1/4，变桨距控制改善了启动性能，且输出功率更加平稳。

(3) 主动式变桨距规律有效地提高了风能利用率，变桨距控制下的风能利用率达到39.12%，几乎是定桨距垂直轴风力机风能利用率的2倍。可见设计的主动式变桨距控制规律可显著提高垂直轴风力机的启动性能和风能利用率。

参考文献：

[1] Wang S Y, Ingham D B, Ma L, et al. Numerical investigations on dynamic stall of low Reynolds number flow around oscillating airfoils[J]. Computers & Fluids, 2010, 39(9): 1529-1541.

[2] Aslam B M M, Hayat N, Farooq A U, et al. Vertical axis wind turbine-A review of various configurations and design techniques[J]. Renewable and Sustainable Energy Reviews, 2012, 16(4): 1926-1939.

[3] Ross I, Altman A. Wind tunnel blockage corrections: Review and application to Savonius vertical-axis wind turbines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(5): 523-538.

[4] Carlos S F, Gijs V K, Gerard V B, et al. Visualization by PIV of dynamic stall on a vertical axis wind turbine[J]. Experiments in Fluids, 2009, 46(1): 97-108.

[5] Dominy R G, Lunt P, Bickerdyke A, et al. Self-starting capability of a darrieus turbine[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2007, 221(1): 111-120.

[6] Paraschivoiu I, Trifu O, Saeed F. H-Darrieus wind turbine with blade pitch control[J]. International Journal of Rotating Machinery, 2009, 505343-1-505343-7.

[7] Pryor D H. Wind turbine with adjustable airfoils: USA，US4383801[P]. 1983-05-17.

[8] Pawsey N C K. Development and evaluation of passive variable-pitch vertical axis wind turbines[D]. Sydney, Australia: University of New South Wales, 2002: 15-21.

[9] Drees H M. The cycloturbine and its potential for broad application[C]//Proceedings of 2nd International Symposium on Wind Energy Systems. Amsterdam, Netherlands, 1978: E7-81-E7-88.

[10] Grylles W, Dale B, Sarr P. A theoretical and experimental investigation into the variable pitch vertical axis wind turbine[C]//The 2nd International Symposium on Wind Energy Systems. Amsterdam, Netherlands, 1978: E9-101-E9-108.

[11] 张亮, 罗庆杰, 韩荣贵. 垂直轴潮流能水轮机叶片偏角优化[J]. 哈尔滨工业大学学报, 2011, 42(1): 281-285.

ZHANG Liang, LUO Qingjie, HAN Ronggui. Optimization of blade deflection angle of vertical-axis tidal current turbine[J]. Journal of Harbin Institute of Technology, 2011, 42(1): 281-285.

[12] 李志川, 孙科, 荆丰梅, 等. 固定偏角垂直轴潮流水轮机叶片安装角研究[J]. 哈尔滨工程大学学报, 2011, 32(7): 853-857.

LI Zhichuan, SUN Ke, JING Fengmei, et al. Study on the blade preset pitch of a fixed pitch vertical axis tidal turbine[J]. Journal of Harbin Engineering University, 2011, 32(7): 853-857.

[13] 张松, 刘秉昊, 张立勋, 等. 基于双多流管模型的同步变桨垂直轴风力机特性分析[J]. 哈尔滨工程大学学报, 2011, 32(8): 1040-1044.

ZHANG Song, LIU Binghao, ZHANG Lixun, et al. Characteristic analysis of a synchronous variable-pitch vertical axis wind turbine based on a double-multiple streamtube model[J]. Journal of Harbin Engineering University, 2011, 32(8): 1040-1044.

[14] A, Chantzidakis M. Development of a hydraulic control mechanism for cyclic pitch marine current turbines[J]. Renewable Energy, 2007, 32(4): 662-679.

[15] Hwang I S, Lee Y H, Kim S J. Optimization of cycloidal water turbine and the performance improvement by individual blade control[J]. Applied Energy, 2009, 86(9): 1532-1540.

[16] Beri H, Yao Y X. Double multiple stream tube model and numerical analysis of vertical axis wind turbine[J]. Energy and Power Engineering, 2011, 3(3): 262-270.

[17] Castelli M R, Englaro A, Benini E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD[J]. Energy, 2011, 36(8): 4919-4934.

[18] Howell R, Oin N, Edwards I, et al. Wind tunnel and numerical study of a small vertical axis wind turbine[J]. Renewable Energy, 2010, 35: 412-422.

(编辑  杨幼平)

收稿日期：2012-07-20；修回日期：2012-09-14

基金项目：中央高校基本科研经费资助项目(HEUCF110707)；黑龙江省科技计划项目(TA09Q801)

通信作者：梁迎彬(1986-)，男，河北保定人，博士，从事垂直轴风力机流固耦合特性研究；电话：0451-82569486，E-mail：lyingbin@163.com