DOI: 10.11817/j.issn.1672-7207.2020.07.008
基于一种分数时滞状态闭环泛函的量化采样系统稳定性分析
陈刚1, 2,陈云1, 2,王炜1, 2,李亚琦1
(1. 湖南工业大学 电气与信息工程学院,湖南 株洲,412007;
2. 电传动控制与智能装备湖南省重点实验室,湖南 株洲,412007)
摘要:对量化采样系统的稳定性问题进行研究。首先,基于Lyapunov-Krasovskii稳定性分析理论,通过在量化采样系统的采样区间内定义1个分数时滞状态,建立1个新的状态空间模型。其次,构造1个全新的分数时滞状态闭环泛函,这种泛函充分利用从tk到t-λμ(t)、从t-λμ(t)到t和从t到tk+1的区间状态信息。然后,根据这种新颖的分数时滞状态闭环泛函、用来估计泛函导数的二阶广义自由权积分不等式和一些含自由权矩阵的恒零等式,得出有量化和无量化采样系统的稳定判据。研究结果表明:基于分数时滞状态闭环泛函所得到的稳定性判据具有较低的保守性。
关键词:采样系统;稳定性;量化;Lyapunov-Krasovskii泛函
中图分类号:TP273 文献标志码:A
文章编号:1672-7207(2020)07-1825-07
Stability analysis for sampled-data systems with quantization based on a fractional delay state looped function
CHEN Gang1, 2, CHEN Yun1, 2, WANG Wei1, 2, LI Yaqi1
(1. School of Electrical and Information Engineering, Hunan University of Technology, Zhuzhou 412007, China;
2. Key Laboratory for Electric Drive Control and Intelligent of Hunan Province, Zhuzhou 412007, China)
Abstract: The stability problem for sampled-data systems with quantization was studied.Firstly, based on the Lyapunov-Krasovskii stability analysis theory,a new state space model was established by defining a fractional delay state in the sampling interval of sampled-data system with quantization. Secondly, a new fractional delay state looped function was constructed for the sampled-data system, which fully utilized the state information from tk to t-λμ(t), t-λμ(t) to t and t to tk+1. Based on this new looped functional of fractional delay state function,two-order generalized free weight integral inequality for estimating function derivatives and some constant-zero equations with free weight matrix, two asymptotic stability criteria for quantization and non-quantization of the sampled-data systems with quantization were derived. Finally, the simulation and numerical examples were used to verify the stability criteria. The results show that the obtained stability criterions based on the fractional delay state looped function are less conservative.
Key words: sampled-data system; stability; quantization; Lyapunov-Krasovskii function
采样系统广泛应用于数字控制系统和网络控制系统,并随着基于事件触发和自触发控制技术的出现,采样系统的研究已经成为当今控制领域最热门的方向之一[1-2]。在实际应用中,1个系统的稳定与否是决定整个系统能否正常运行的前提保障,对系统的稳定性进行研究具有重要的理论意义与实际意义[3]。为了分析采样系统的稳定性,有如下3种基础分析方法:将采样系统转化为离散系统的离散系统模型方法[4-5];将采样系统转化为跳变系统的脉冲系统方法[6];基于李亚普诺夫泛函并将采样系统转化为时滞系统的输入时滞方法[7-8]。为了放松泛函中矩阵正定的限制,SEURET等[9] 基于以上3种方法,结合混沌动态系统方法与脉冲系统方法,提出了一种依赖转换泛函状态的闭环泛函分析方法。在此基础上,SEURET[10]给出了1个基于Wirtinger积分不等式的稳定性判据,获得了更大的稳定采样区间上界。LEE等[11]采用基于自由权矩阵积分不等式的时滞相关不连续李亚普诺夫方法研究了采样系统稳定性,再一次改进了采样系统的稳定性判据。在文献[4-11]的方法中,都只关注了从tk到t的采样区间信息,却忽视了从t到tk+1的采样区间信息。ZENG等[12]提出了2个采样区间都考虑的新闭环泛函,得到了接近理论分析值的稳定性判据。然而,以上研究仿真实例结果与由经典特征值分析法所得结果相比,仍存在一些不足。另一方面,在数字控制系统与网络控制系统中,信号通过网络传输之前需要经过量化器处理,量化器可以看成一类非线性映射,将实数集的不同段映射到不同水平。由于字长有限,量化误差不可避免且降低系统性能[13-14]。长期以来,对量化的研究一直是人们关注的焦点[15-19]。利用离散系统模型,HOU等[15]研究了量化采样系统的稳定性问题。ISHII等[16-17]给出了量化采样系统稳定的无记忆量化器的设计方法和随机算法,但所使用的处理量化误差的方法仅仅关注了系统稳定性问题,没有考虑系统的性能。为解决此问题,FU等[18]提出了量化误差可以用扇区有界的不确定性或非线性处理,这样,鲁棒控制分析方法可用于研究量化误差对采样系统的影响。基于FU等[18]提出的处理量化误差的方法,SHAO等[19]通过构造了1个分段可微的李雅普诺夫泛函,得出了量化采样系统的指数和渐进稳定性判据,但所使用的时滞分析方法保守性很大,需进一步改进。为此,本文作者对量化采样系统的稳定性问题进行研究。首先,在采样区间内,引入1种分数时滞状态空间模型,然后构造1个充分利用从tk到t-λμ(t),从t-λμ(t)到t和从t到tk+1的区间状态信息的全新闭环泛函。结合二阶广义自由权矩阵积分不等式和含自由权矩阵的恒零等式,得到采样系统有量化和无量化这2个稳定性判据。最后,通过数例仿真对比其他文献结果证明这2个稳定性判据的有效性和优越性。
1 问题描述
定义如下符号:上标T和-1分别表示矩阵或矢量的转置和求逆; n和
n和 n×m分别表示实数域的n维向量空间和n×m维的矩阵空间;矩阵P>0表示矩阵P为对称正定矩阵;0和I分别为零矩阵和单位矩阵;在块矩阵中,
n×m分别表示实数域的n维向量空间和n×m维的矩阵空间;矩阵P>0表示矩阵P为对称正定矩阵;0和I分别为零矩阵和单位矩阵;在块矩阵中, 表示对称项;P为矩阵;Sym{P}表示P+PT;diag{b1,
表示对称项;P为矩阵;Sym{P}表示P+PT;diag{b1, ,bn}代表块对角矩阵;col{b1,…,bn}表示一组列向量,其中,b1,…,bn代表任意矩阵或向量。
,bn}代表块对角矩阵;col{b1,…,bn}表示一组列向量,其中,b1,…,bn代表任意矩阵或向量。
考虑如下量化采样系统:
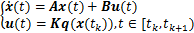 (1)
(1)
式中:
 n,为系统状态向量;A和B为有合适维度的系统矩阵;状态量化控制输入
n,为系统状态向量;A和B为有合适维度的系统矩阵;状态量化控制输入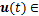
 m;K为系统控制增益矩阵;
m;K为系统控制增益矩阵;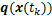 表示量化器
表示量化器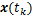 的量化值。
的量化值。
采样瞬间tk+1和tk满足tk+1-tk=hk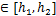 ,且
,且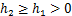 ,其中,
,其中, 和
和 分别代表采样区间最上界和最下界。
分别代表采样区间最上界和最下界。
量化器是对称的,qi(-xi(tk))=-qi(xi(tk)),可描述为
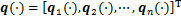 (2)
(2)
其量化级数集合υ为
 (3)
(3)
其中:ρ为量化密度且满足0<ρ<1,初始量化υ0>0。
式(2)中的量化器 可以定义为
可以定义为
 (4)
(4)
其中:量化器参数 ;i=1,2,…,n。
;i=1,2,…,n。
与文献[19]中结果类似,当xi(tk)≥0时,有
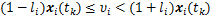 (5)
(5)
当xi(tk)<0时,有
 (6)
(6)
所以,量化器可以描述为
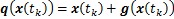 (7)
(7)
 (8)
(8)
其中,g(x(tk))为非线性函数并满足
 (9)
(9)
量化采样系统模型可以改写成
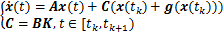 (10)
(10)
当系统没有状态量化时,无量化采样系统模型为
 (11)
(11)
定义1:分数时滞状态的采样系统状态定义为x(t-λμ(t)),其中, ,
, ,
,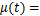
 。
。
基于以上定义,可以得出如下状态空间模型:

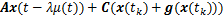 (12)
(12)
注释1:这种状态空间模型与时滞系统中的状态分割思想类似,但不同之处在于这里 ,不能直接在时滞系统中使用。但在量化采样系统的稳定性分析中,计算量不复杂和在构建的泛函中增加了状态信息x(t-λμ(t)),这使得其能够很好地得到应用。
,不能直接在时滞系统中使用。但在量化采样系统的稳定性分析中,计算量不复杂和在构建的泛函中增加了状态信息x(t-λμ(t)),这使得其能够很好地得到应用。
引理1:给出正定对称矩阵
 n×n和任意矩阵
n×n和任意矩阵
 n×k(i=1,2,3),对于任意可导函数
n×k(i=1,2,3),对于任意可导函数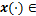

 n,
n,
 n×k,
n×k,
 n×k(j=1,2)和向量
n×k(j=1,2)和向量
 k,有如下不等式成立:
k,有如下不等式成立:
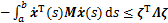 (13)
(13)
其中:
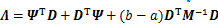 ;
;
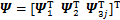 ;
; ;
;
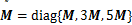 ;
; ;
;
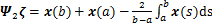 ;
;

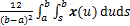 ;
;

 。
。
注释2:引理1是基于文献[12,20-21]所得,是一种二阶广义自由权矩阵积分不等式。这种积分不等式的优势在于估计积分项时不需要使用逆凸技术,与文献[10]中的积分不等式相比,分析系统的稳定性效果更好。
2 主要结果
在给出主要定理之前,有如下定义:
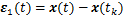 ;
;
 ;
;
 ;
;
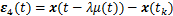 ;
;
 ;
;
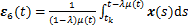 ;
;
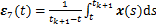 ;
;
 ;
;
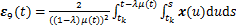 ;
;
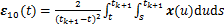 ;
;
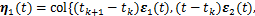
 ;
;
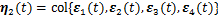 ;
;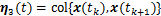 ;
;
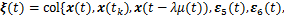
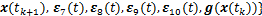 ;
;
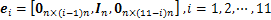 ;
;
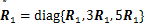 ;
; ;
;
 ;
;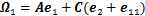 ;
;
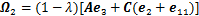 ;
;
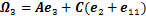 。
。
定理1:给定标量h1,h2和 ,存在矩阵P>0,R1>0,R2>0和R3>0,且存在具有合适维数的任意矩阵S1,S2,Z1,Z2,Z3,Q,G,M1,M2,M3,H1,H2,H3,H4,H5和H6,对角矩阵N>0,对于hk
,存在矩阵P>0,R1>0,R2>0和R3>0,且存在具有合适维数的任意矩阵S1,S2,Z1,Z2,Z3,Q,G,M1,M2,M3,H1,H2,H3,H4,H5和H6,对角矩阵N>0,对于hk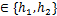 ,有线性矩阵不等式
,有线性矩阵不等式
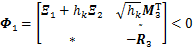 (14)
(14)
 (15)
(15)
成立,则系统(10)渐近稳定。式中:
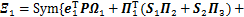
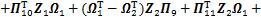
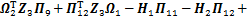

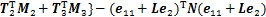 ;
;
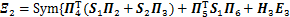
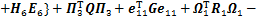
 ;
;
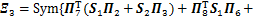
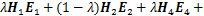
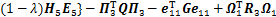 ;
;
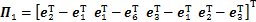 ;
;
 ;
;
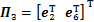 ;
; ;
;
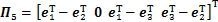 ;
;
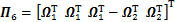 ;
;
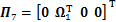 ;
;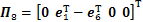 ;
;
 ;
;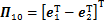 ;
;
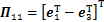 ;
;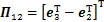 ;
;
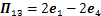 ;
;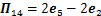 ;
;
 ;
; ;
;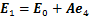 ;
;
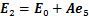 ;
;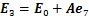 ;
; ;
;
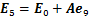 ;
; ;
;
 ;
;
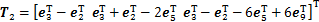 ;
;
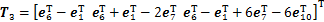 。
。
证明:首先构造含分数时滞状态的泛函:
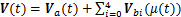 (16)
(16)
其中:
 ;
;
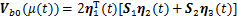 ;
;
 ;
;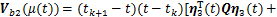
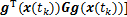 ;
;
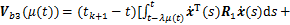
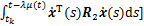 ;
;
 。
。
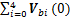 =
=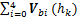 ,故泛函V(t)是闭环函数,从而矩阵S1,S2,Z1,Z2,Z3,Q和G不需要满足正定条件,经求导可得:
,故泛函V(t)是闭环函数,从而矩阵S1,S2,Z1,Z2,Z3,Q和G不需要满足正定条件,经求导可得:
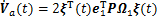 ;
;
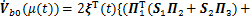


 ;
;


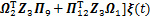 ;
;
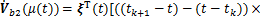
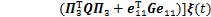 ;
;

 ;
;
 。
。
其中:
 ;
;
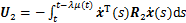 ;
;
 。
。
用引理1估计上面3个积分项,可得:
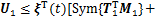
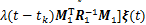 ;(17)
;(17)
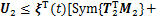
 ;(18)
;(18)

 。(19)
。(19)
然后,根据式(9)可得
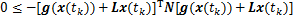 (20)
(20)
即
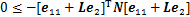 (21)
(21)
其中:L=diag{l1,l2,…,ln}。
类似文献[12],有如下零矩阵等式:
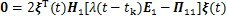 (22)
(22)
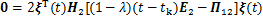 (23)
(23)
 (24)
(24)
 (25)
(25)
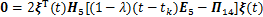 (26)
(26)
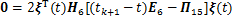 (27)
(27)
综上所述,可得
 (28)
(28)
其中: ;
;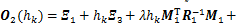
 。
。
运用Schur补定理,若式(14)和(15)成立,则有 和
和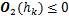 ,即
,即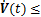 0,故量化采样系统(10)渐近稳定。证明完毕。
0,故量化采样系统(10)渐近稳定。证明完毕。
注释3:定理1提供了1个量化采样系统稳定性判据。与文献[19]中方法相比,本文构建了含更多状态信息的泛函以及使用了更紧密估计泛函的积分不等式方法。
注释4:由泛函的定义可知,与文献[12]相比,本文泛函引入了分数时滞状态,状态区间变成了从tk到t-λμ(t),从t-λμ(t)到t和从t到tk+1,这使稳定性判据的保守性得到减少。为进一步突出本文方法优于相关文献中的方法,考虑采样系统无量化的情形,给出如下定理。
定理2:给定标量h1,h2和 ,存在正定对称矩阵P>0,R1>0,R2>0和R3>0,且存在具有合适维数的任意矩阵S1,S2,Z1,Z2,Z3,Q,M1,M2,M3,H1,H2,H3,H4,H5和H6,对于hk
,存在正定对称矩阵P>0,R1>0,R2>0和R3>0,且存在具有合适维数的任意矩阵S1,S2,Z1,Z2,Z3,Q,M1,M2,M3,H1,H2,H3,H4,H5和H6,对于hk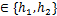 ,有线性矩阵不等式
,有线性矩阵不等式
 (29)
(29)
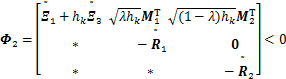 (30)
(30)
成立,则系统(11)渐近稳定。式中:
 ;
;
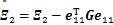 ;
;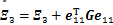 ;
;
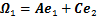 ;
; ;
;
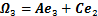 ;
;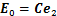 。
。
其他变量与定理1中的定义一致。
证明:在向量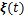 中删除
中删除 项,并在其对应的
项,并在其对应的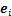 减少一维选择泛函时去除
减少一维选择泛函时去除 项,其证明过程与定理1的证明过程相似。
项,其证明过程与定理1的证明过程相似。
注释5:邵汉永等[3]提出在构建泛函时加入状态积分项有利于改善采样系统的稳定性判据,因此,对于一些基于采样的控制问题,可在本文的泛函基础上扩展一些状态积分项,如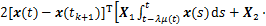
 和
和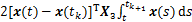 。
。
3 仿真实例
例1考虑量化采样系统模型(10),其中,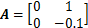 ,
,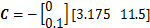 ,
,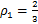 ,
, 。量化参数分别为
。量化参数分别为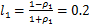 ,
,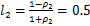 。
。
给出
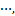 0.990 0,
0.990 0, 和采样区间下界h1=10-5。由文献[19]和根据定理1所得的采样区间上界h2分别为1.121 5和3.076 4,可见由本文方法所得结果相比文献[19]中结果提高了174%,这说明本文所获得的量化采样系统渐进稳定性判据的保守性小。
和采样区间下界h1=10-5。由文献[19]和根据定理1所得的采样区间上界h2分别为1.121 5和3.076 4,可见由本文方法所得结果相比文献[19]中结果提高了174%,这说明本文所获得的量化采样系统渐进稳定性判据的保守性小。
不同的λ所得的最大采样区间上界h2如图1所示。由图1可知:当λ=0.06时,h2取最大值3.076 4,这同时也说明分数时滞状态的闭环泛函方法具有一定的可行性。
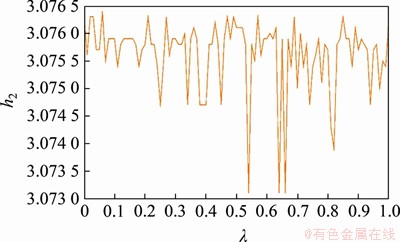
图1 例1中不同λ下的采样区间上界h2
Fig. 1 Upper bound h2 of sampling interval under different λ in Example 1
为了进一步说明本文方法的优越性,考虑如下无量化采样系统仿真实例。
例2 考虑无量化采样系统模型(11),其中,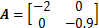 ,
,
给出 0.990 0,
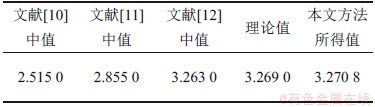
0.990 0,  和采样区间下界h1=10-5。表1所示为根据本文定理2和文献[10-12]以及传统特征值分析法所得的采样区间上界h2。由表2可知:与文献[10-12]中结果对比,由本文定理2所得的h2较大,可知本文提出的基于分数时滞状态闭环泛函方法具有明显的优越性。值得注意的是,本文所得采样区间上界已略大于理论值,这也说明该例采用特征值分析法所得精度具有一定的保守性。
和采样区间下界h1=10-5。表1所示为根据本文定理2和文献[10-12]以及传统特征值分析法所得的采样区间上界h2。由表2可知:与文献[10-12]中结果对比,由本文定理2所得的h2较大,可知本文提出的基于分数时滞状态闭环泛函方法具有明显的优越性。值得注意的是,本文所得采样区间上界已略大于理论值,这也说明该例采用特征值分析法所得精度具有一定的保守性。
表1 例2中采样区间上界h2
Table 1 The maximum upper bound of h2 in Example 2
取 所得最大采样上界h2如图2所示。由图2可知:当λ=0.51~0.53时,h2取最大值3.270 8。
所得最大采样上界h2如图2所示。由图2可知:当λ=0.51~0.53时,h2取最大值3.270 8。
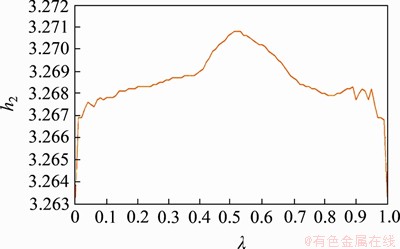
图2 例2中不同λ下的采样区间上界h2
Fig. 2 Upper bound h2 of sampling interval under different λ in Example 2
4 结论
1) 研究了量化采样系统渐进稳定性问题。基于一种分数时滞状态空间,构建了1个全新的闭环泛函,用1个二阶广义自由权积分不等式估计了这个泛函的导数,同时加入了一些含自由权矩阵的恒零等式,推导出基于线性矩阵不等式的有量化和无量化采样系统稳定性判据。
2) 在数值实例仿真中,通过求解线性矩阵不等式,发现这2个渐进稳定性判据具有明显的优势。
3) 本文方法可用于解决其他基于采样控制的控制问题,如基于采样的网络系统同步控制和基于采样的网络系统H∞控制问题。
参考文献:
[1] HETEL L, FITER C, OMRAN H, et al. Recent developments on the stability of systems with aperiodic sampling: an overview[J]. Automatica, 2017, 76: 309-335.
[2] ZENG Hongbing, TEO K L, HE Yong, et al. Sampled-data stabilization of chaotic systems based on a T-S fuzzy model[J]. Information Sciences, 2019, 483: 262-272.
[3] 邵汉永, 赵建荣, 张丹. 关于变周期采样系统稳定性分析的新Lyapunov泛函方法[J]. 控制与决策, 2017, 32(1): 167-170.
SHAO Hanyong, ZHAO Jianrong, ZHANG Dan. Lyapunov functional approach to stability of sampled-data systems under aperiodic sampling[J]. Control and Decision, 2017, 32(1): 167-170.
[4] SUH Y S. Stability and stabilization of nonuniform sampling systems[J]. Automatica, 2008, 44(12): 3222-3226.
[5] FUJIOKA H. A discrete-time approach to stability analysis of systems with aperiodic sample-and-hold devices[J]. IEEE Transactions on Automatic Control, 2009, 54(10): 2440-2445.
[6] NAGHSHTABRIZI P, HESPANHA J P, TEEL A R. Exponential stability of impulsive systems with application to uncertain sampled-data systems[J]. Systems & Control Letters, 2008, 57(5): 378-385.
[7] FRIDMAN E. A refined input delay approach to sampled-data control[J]. Automatica, 2010, 46(2): 421-427.
[8] LIU Kun, FRIDMAN E. Wirtinger's inequality and Lyapunov-based sampled-data stabilization[J].Automatica, 2012, 48(1): 102-108.
[9] SEURET A. A novel stability analysis of linear systems under asynchronous samplings[J]. Automatica, 2012, 48(1): 177-182.
[10] SEURET A, GOUAISBAUT F. Wirtinger-based integral inequality: application to time-delay systems[J]. Automatica, 2013, 49(9): 2860-2866.
[11] LEE T H, PARK J H. Stability analysis of sampled-data systems via free-matrix-based time-dependent discontinuous Lyapunov approach[J]. IEEE Transactions on Automatic Control, 2017, 62(7): 3653-3657.
[12] ZENG Hongbing, TEO K L, HE Yong. A new looped-functional for stability analysis of sampled-data systems[J]. Automatica, 2017, 82: 328-331.
[13] 陈刚, 陈云, 王炜. 基于量化控制的网络系统稳定性分析[J]. 中南大学学报(自然科学版), 2019, 50(9): 2156-2162.
CHEN Gang, CHEN Yun, WANG Wei. Stability analysis for network system based on quantitative control[J]. Journal of Central South University(Science and Technology), 2019, 50(9): 2156-2162.
[14] 王兴成, 李放文, 赵承心. 不确定性网络系统的量化H∞控制[J]. 中南大学学报(自然科学版), 2011, 42(Z1): 392-398.
WANG Xingcheng, LI Fangwen, ZHAO Chengxin. Quantized H∞ control for uncertain networked system[J]. Journal of Central South University (Science and Technology), 2011, 42(Z1): 392 -398.
[15] HOU Ling, MICHEL A N, YE H. Some qualitative properties of sampled-data control systems[J]. IEEE Transactions on Automatic Control, 1997, 42(12): 1721-1725.
[16] ISHII H, FRANCIS B A. Quadratic stabilization of sampled-data systems with quantization[J]. Automatica, 2003, 39(10): 1793-1800.
[17] ISHII H, BASAR T, TEMPO R.Randomized algorithms for quadratic stability of quantized sampled-data systems[J]. Automatica, 2004, 40(5): 839-846.
[18] FU Minyue, XIE Lihua. The sector bound approach to quantized feedback control[J]. IEEE Transactions on Automatic Control, 2005, 50(11): 1698-1711.
[19] SHAO Hanyong, HAN Qinglong, ZHANG Zhengqiang, et al. Sampling-interval-dependent stability for sampled-data systems with state quantization[J]. International Journal of Robust and Nonlinear Control, 2014, 24(17): 2995-3008.
[20] CHEN Yun, CHEN Gang. Stability analysis of systems with time varying delay via a novel Lyapunov functional[J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(4): 1068-1073.
[21] ZENG Hongbing, HE Yong, WU Min, et al. New results on stability analysis for systems with discrete distributed delay [J]. Automatica, 2015, 60: 189-192.
(编辑 陈灿华)
收稿日期: 2019 -10 -08; 修回日期: 2019 -12 -15
基金项目(Foundation item):湖南省自然科学基金资助项目(2018JJ4075);国家自然科学基金资助项目(61703153,61673166) (Project(2018JJ4075) supported by the Natural Science Foundation of Hunan Province; Projects(61703153, 61673166) supported by the National Natural Science Foundation of China)
通信作者:王炜,副教授,从事时滞系统、鲁棒控制和网络控制系统研究;E-mail:wangwei9804@163.com