采场岩移规律现场监测试验及时间序列预报

赵国彦，刘立顺，栗红玉，刘强

(中南大学 资源与安全工程学院，湖南 长沙，410083)

摘要：结合新城金矿开采实际，设计顶板岩移监测方案，分析监测数据，并进行岩移变形时间序列预报。采场顶板监测表明：每2 d岩移量在-2.00~2.00 mm之内，100 d累计岩移量不超过20.00 mm；最大岩移量位于顶板中心，最小岩移量位于采场两帮；岩移量沿采场走向呈现出先增后减的规律；岩移量随时间逐渐趋于稳定，顶板累计岩移量不超过25.00 mm；矿山目前支护方式可确保采场安全；采场支护应在岩层应力完全释放前进行，锚杆网度应根据现场情况适当加大。

关键词：采矿；现场监测；岩移量；时间序列

中图分类号：TU45          文献标志码：A         文章编号：1672-7207(2012)06-2300-08

Safety monitoring test and time series predicting analysis for roof support

ZHAO Guo-yan, LIU Li-shun, LI Hong-yu, LIU Qiang

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Abstract: According to mining condition of Xincheng Gold Mine, the monitoring scheme for roof displacement was designed and the results data were analyzed, and then the time series predicting analysis for roof support was made. The results show that the rockbody movement value range from -2 mm to 2 mm every 2 d, with an overall change of 20 mm for 100 d. In the same drift section, the maximum value of roof rock movement amount appears frequently at the middle point and the minimum in the stope’s sides. Along the stope trend, the movement value increases at first and then decreases. Cumulative rock movement amount gradually tends to be in equilibrium, with a maximum value of 25 mm. Based on the results of roof movement monitoring and prediction, the existing support way can effectively ensure that the safety and reliability of the stope roof shall be obtained. It is advised that roof support should be taken before stress release is finished and that the support netextent should be increased according to the practical situation on site.

Key words: mining; monitoring of roof displacement; rock movement amount; time series

在矿山开采过程中，由于矿岩的非均质性与多重应力场的叠加，给理论分析岩层变形规律增加了极大难度，引起采场支护设计失误，造成采场顶板应力集中，安全事故频繁发生。近年来，国内外相关学者对采场岩体受力和变形监测的研究取得了重大的理论成果^[1-2]。结果表明：现场监测有利于掌握采场岩体和支护系统的力学动态，及时掌握施工效果和施工安全，适时调整施工参数，优化结构，提高工效和降低成本，确保日常施工的信息化管理。目前，矿山现场监测应用范围不断扩大^[3]，现已广泛应用于介质力学参数反演、施工超前预报、支护时间设置、信息化设计和施工效果检验等方面。随着工程技术水平的提高，现场监测在仪器方面正在向“可移动”和“高档化”方向发展；在监测方案设计方面越来越重视以各种信息综合集成结果为基础的设计方法，在信息反馈方面越来越重视工程监测的实用性。现阶段的现场监测虽取得了一定的研究成果，但仍存在监测方案不完善和监测数据分析存在缺陷等不足。为此，本文作者以山东黄金矿业股份有限公司新城金矿-630中段63762试验采场为工程背景，对支护后的采场顶板进行监测方案设计，并对所得监测数据处理和分析，进而获得采场岩体变形规律。运用时间序列对监测数据进行预报，充分考虑时间因素影响，掌握采场岩体变形发展趋势。在此基础上评价采场顶板岩体稳定性，提出支护优化方案。

1  监测方案与数据处理

1.1  监测方案

新城金矿762试验采场采用预控顶中深孔落矿嗣后充填采矿法，采场预控顶巷道位于-620 m水平，顶板宽8.8 m，高3.2 m，采用预应力锚杆+锚网+喷浆联合支护。结合采场情况，采用顶板岩移监测获取顶板动态发展变化规律^[4-6]。

顶板岩移监测采用巷道变形收敛仪^[7]，在预控顶巷道内设2组监测断面，每组5个测点。每个断面内的测点采用三角形布点法安设，如图1所示。顶部3个测点分别布置在距离巷道南帮边界2.2，4.4和6.6 m处的顶板表面；帮部测点布置在边帮表面，距离底板1.6 m高处。同一测面上的5个测点要求在同一垂直 面内。

测点用木桩标定。施工方法为：用7665浅孔钻机钻直径为32 mm、深为380 mm的孔，将直径为34 mm、长为400 mm的木桩打入孔中，木桩端部安设弯形测钉。安装要求：木桩轴线应与巷道壁面垂直；木桩打入孔后，与钻孔紧密结合，无松动现象。监测频率为每2 d 1次。在监测过程中，若位移速度发生突然变化或出现其他突发事件，则加强监测。

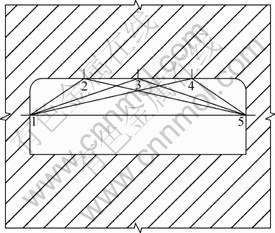
图1  顶板岩移监测测点布置剖面图

Fig.1  Monitoring points arrangement for roof rock movement

1.2  数据计算

1.2.1  岩移量计算

收敛计所测数据为各监测桩点之间的距离，顶板岩移量通过计算获得。计算简图见图2，计算公式为：

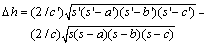        (1)

式中：s=(a+b+c)/2；。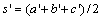

图2  监测断面位移计算简图

Fig.2  Dsplacement calculation for monitoring section

1.2.2  数据检测与插值

监测数据混有粗差值将会影响分析预测结果，在进行数据分析和预测之前需进行检测。根据监测数据数量，选择格拉布斯准则进行检测，剔除不合格数据。

由于主、客观条件的限制并剔除了不合格数据，监测数据出现“断链”现象。采用3次多项式插值法对“断链”处的数据插补，通过MATLAB软件实现。

2  结果与分析

2.1  顶板岩移量随时间变化关系

各断面顶板岩移量随时间变化关系见图3~4。

从图3可看出：A断面各监测点每2 d岩移量的变化(单次岩移量)在-2.00~2.00 mm范围内，并随时间增长逐渐减小，但趋势不明显。累计岩移量随时间逐渐增大，趋势变缓，监测期内累计岩移量不超过20.00 mm。在喷浆施工期间，有较长时间监测中断，前后2次岩移量变化较大，间隔长是导致这一现象的主要原因。将监测值变化差分到监测周期内，则每2 d岩移量变化较小，原因是喷浆支护减缓了顶板下沉速率，喷浆支护对岩移变化速率有较明显影响。

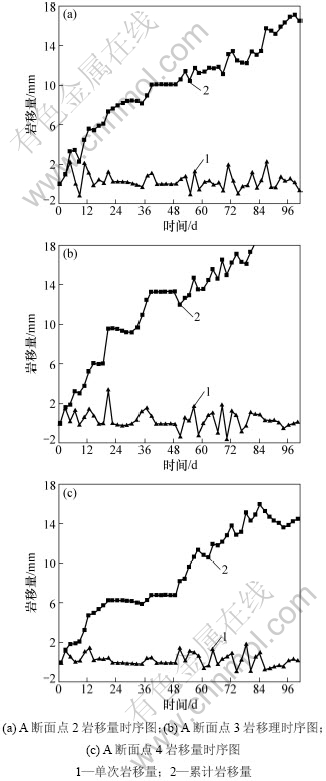
图3  A断面点2,3和4顶板岩移随时间变化关系

Fig.3  Relationship between roof rock movement and time at points 2, 3 and 4 in section A

从图4可看出：B断面各监测点每2 d岩移量变化(单次岩移量)在-2.00~2.00 mm范围内，随时间变化规律与A断面相同，监测期内累计岩移量不超过12.00 mm。B断面累计岩移量比A断面的小，主要原因是B断面靠近端部，岩移量较中间位置变化小。

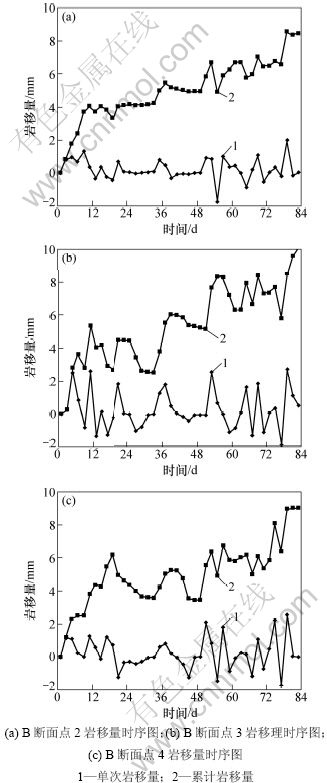
图4  B断面点2,3和4顶板岩移随时间变化关系

Fig.4  Relationship between roof rock movement and time at points 2, 3 and 4 in section B

2.2  同断面内顶板岩移量变化关系

提取累积时间分别为20，40，60，80和100 d的累计岩移量进行对比分析，同断面内顶板岩移量空间变化关系见图5~6。

结合图1巷道测点的位置，由图5可看出：A断面内顶板累计岩移量最大值在监测点3处，监测点2和4累计岩移量均小于监测点3，两侧帮处岩移量基本为0 mm。

结合图1巷道测点的位置，由图6可看出：B断面内顶板累计岩移量最大值在监测点3处，监测点2和4累计岩移量均比监测点3的小，两侧帮处岩移量基本为0 mm。分析同断面顶板岩移量变化可看出：在同一断面内，顶板累计岩移量最大值位于中心线上，由中心向两帮逐渐减小。

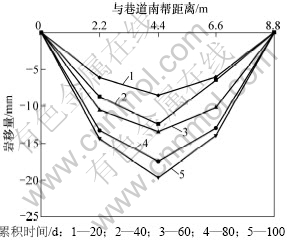
图5  A断面顶板岩移量变化关系

Fig.5  Variation relation between roof rock movement amount in section A

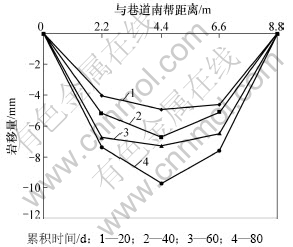
图6  B断面顶板岩移量变化关系

Fig.6  Variation relationship between roof rock movement amount in section B

2.3      顶板岩移量与采场走向长度变化关系

提取累积时间分别为20，40，60和80 d的累计岩移量进行对比分析，顶板岩移量与采场走向长度变化关系见图7~9。

结合图1巷道测点的位置，从图7可看出：各断面2点顶板岩移量随时间增大；从上盘到下盘，各断面2点顶板岩移量先增大后减小。顶板岩移量在80 d时接近14 mm。

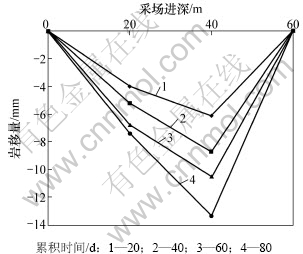
图7  点2顶板岩移量与采场走向长度变化关系

Fig.7  Relationship between roof rock movement amount and roadway depth of point 2

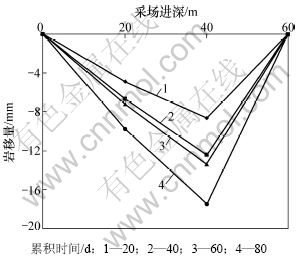
图8  点3顶板岩移量与采场走向长度变化关系

Fig.8  Relationship between roof rock movement amount and roadway depth of point 3

结合图1巷道测点的位置，从图8可看出：顶板岩移量在80 d时接近18 mm。

结合图1巷道测点的位置，从图9可看出：顶板岩移量在80 d时接近15 mm。分析顶板岩移量与走向关系可得出：从上盘到下盘，顶板岩移量先增大后减小。居中位置岩移量最大。在中心线上该变化趋势更为突出(点3顶板岩移量较点2和4的顶板岩移量   都大)。

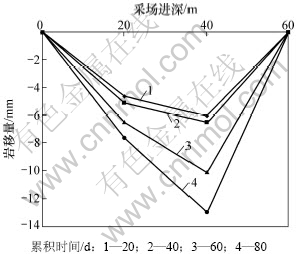
图9  点4顶板岩移量与采场走向长度变化关系

Fig.9  Relationship between roof rock movement amount and roadway depth of point 4

3  时间序列预报

目前常用的预报方法和模型有回归分析法、灰色理论法、神经网络法和遗传算法等^[8-10]。这些方法都能在各自适用的条件下较好地进行预报分析，但都没有充分考虑时间对预报变量的影响，不能用于本文的顶板岩移量预报。顶板岩移量是随时间变化的数据集，对其预报必须充分考虑时间的影响，时间序列预报方法^[11-17]能满足这一要求。

3.1  趋势项提取

以A断面2点累计岩移量为对象进行分析。由图3(a)可知：A断面2点累计岩移量时间序列有逐渐增加的趋势，基本可以视为非平稳序列。

序列的自相关系数在很长的延迟期间一直为正，而后又一直为负，显示出明显的三角对称性，A断面2点累计岩移量具有非平稳时间序列特性。

采用最小二乘法对监测数据时间序列进行多项式趋势项提取，得趋势项的多项式函数：

y(t)=-0.000 4t²+0.161 3t+2.203 3         (2)

3.2  残差项检验

3.2.1  平稳性检验

提取趋势项后的残差时间序列图见图10。由图10可知：A断面2点累计岩移量残差时序在0附近波动，没有明显趋势或周期，经检验为平稳时序。

3.2.2  纯随机性检验

纯随机性检验通过Ljung-Box(LB)统计量判断，A断面2点累计岩移量残差时序LB统计量相关数据  见表1。

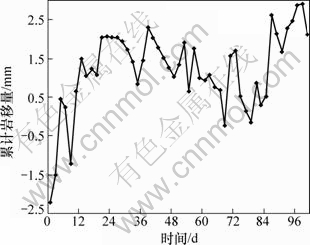
图10  A断面2点累计岩移量残差时序图

Fig.10  Time series error of cumulative rock movement amount of point 2 in section A

表1  LB统计量检验

Table 1  LB statistics test

取α=0.05，由表1知P显著小于α，残差序列不服从纯随机的假设。可采用平稳时间序列对A断面2点累计岩移量残差序列进行统计分析。

3.3  残差项建模

分析得A断面2点累计岩移量残差时序自相关系数与偏自相关系数均具有拖尾性。残差序列满足ARMA(p,q)模型：

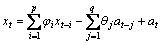        (3)

取p=1，q=1，计算模型参数。

(1) φ_i计算。φ满足下式：

R_A=R_Bφ                  (4)

式中：φ；；

；

R_k为序列的自协方差函数，R_k=E[x_tx_t-k]。

将残差序列值{x_t}代入式(4)，计算得A断面2点累计岩移量残差时序φ₁=0.373 4。

(2) θ_j计算。在ARMA(p,q)模型中，令

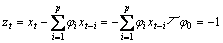    (5)

则有：

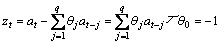    (6)

由谱密度函数关系式，可得：

              (7)

滑动平均部分的B算子多项式θ(B)满足：

        (8)

比较B算子的同次幂系数即可解得θ_j。A断面2点累计岩移量残差时序θ₁=-0.075 4。

(3) 统计检验。若计高、低阶模型阶次分别为p_h和p_l，则构造统计量：

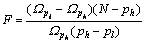           (9)

式中：Ω为残差平方和，Ω=(V^TV)。

F~F(p_h-p_l，N-p_h)，按式(9)计算：当F>F(p_h-p_l，N-p_h)时，表明p_h较p_l有显著性差异，低阶模型不适用，还可升阶建模；反之，则认为低阶模型适用。

经检验，与ARMA(2,1)和ARMA(1,2)相比，ARMA(1,1)模型可用。

综上可见：A断面2点累计岩移量残差时序采用ARMA(1,1)模型，式(10)为模型公式。

x_t=0.373 4x_t-1+0.075 4a_t-1+a_t          (10)

 (4) 时间序列模型。对残差项模型时间还原，并与趋势项模型相加得以下组合模型：

y_t=-0.000 4t²+0.161 3t+2.203 3+0.373 4x_t-2+

0.075 4a_t-2+a_t ，t=2n           (11)

3.4  时间序列模型

通过对累计岩移量时间序列模型相邻两时间点求差，得到单次岩移量时间序列模型。各监测点的累计岩移量时间序列模型见表2，单次岩移量时间序列模型见表3。

表2  各监测点的累计岩移量时间序列模型

Table 2  Time series model of cumulative rock movement amount

表3  各监测点岩移量的时间序列模型

Table 3  Time series model of single rock movement amount

3.5  时间序列预报

对于ARMA(p,q)模型，最佳预报值由下式计算得到：

   (12)

预报方差由下式计算：

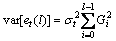            (13)

95%置信区间为：

，

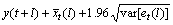       (14)

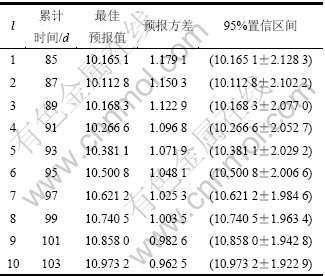
分别对A和B断面3点的累计岩移量进行后10期预报，预报结果见表4和表5。

由表4和表5可知：预报方差与预报值之比为3.0%~11.6%，这与采场活动频繁程度和监测点周围岩体结构发育程度有关。从预报结果可以看出：采场顶板岩移量逐渐趋于稳定，累计岩移量不超过25.00 mm。现有的支护方式能很好地控制岩体位移，保证采场顶板安全稳固，可根据现场条件适当加大锚杆支护网度，缩减成本，加快工期。

表4  A断面点3累计岩移量的后10期预报结果

Table 4  Last 10 periods prediction of point 3 in section A

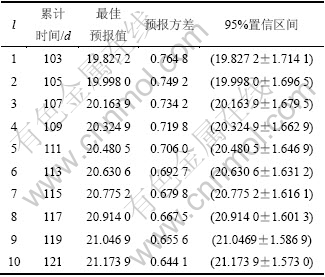
表5  B断面点3累计岩移量的后10期预报结果

Table 5  Last 10 periods prediction of point 3 in section B

4  结论

(1) 采场监测具有监测时间短，数据获取数量有限和数据跳动大的特点。这主要是因为采场存留时间短，数据读取与施工相冲突，变形受施工扰动影响大。

(2) 每2 d的岩移量随着时间推移逐渐减小，但趋势不明显，每2 d的岩移量在-2.00~2.00 mm范围内变化；累计岩移量随着时间推移逐渐趋于稳定，在监测时间内，累计岩移量不超过20.00 mm。喷浆支护对顶板表面变化速率有较明显的影响。

(3) 在同一断面内，顶板累计岩移量最大值位于采场中心线上，最小值位于采场两帮；从采场上盘到采场下盘，各个监测点的岩移量先增大后减小，采场居中位置的岩移量最大。

(4) 通过时间序列预报分析，发现岩移量逐渐趋于稳定，累计岩移量不超过25.00 mm，目前的支护方式能很好地控制岩体位移，保证采场顶板安全稳固。

(5) 通过监测数据分析和预报分析，建议对预控顶支护进行以下修改：采场预控顶支护应在岩层应力完全释放完之前进行；适当加大锚杆支护网度，保证安全，缩减成本，加快工期。

参考文献：

[1] Cravero M, Iabichino G. Geomechanical study for the exploitation of an underground marble quarry[J]. International Journal of Rock Mechanics & Mining Sciences, 1997, 34: 1-14.

[2] Li X B, Dong L J, Zhao G Y, et al. Stability analysis and comprehensive treatment methods of landslides under complex mining environment[J]. Safety Science, 2012, 50(4): 695-704.

[3] 侯建国, 王腾军. 变形监测理论与应用[M]. 北京: 测绘出版社, 2008: 68-133.
HOU Jian-guo, WANG Teng-jun. Theory of deformation monitoring and its application[M]. Beijing: Surveying and Mapping Press, 2008: 68-133.

[4] Shen B, King A, Guo H. Displacement, stress and seismicity in roadway roofs during mining-induced failure[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45: 672-688.

[5] 王其胜. 深部软岩巷道矿压特征与支护技术研究[D]. 长沙: 中南大学资源与安全工程学院, 2008: 18-36.
WANG Qi-sheng. Study on support technology and ground pressure behavior of deep soft rock tunnel[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2008: 18-36.

[6] 朱瑞赓. 岩体结构面力学特征及地下工程结构稳定性的研究[D]. 武汉: 武汉理工大学土木工程与建筑学院, 2001: 68-84.
ZHU Rui-geng. Study of mechanical properties of rock mass structural plane and structural stability of underground construction[D]. Wuhan: Wuhan University of Technology. School of Engineering and Construction, 2001: 68-84.

[7] Simeoni L, Zanei L. A method for estimating the accuracy of tunnel convergence measurements using tape distometers[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 796-802.

[8] Ture M, Kurt I. Comparison of four different time series methods to forecast hepatitis airus infection[J]. Expert Systems with Application, 2006, 31: 41-46.

[9] Juhos I, Makra L, Toth B. Forecasting of traffic origin NO and NO₂ concentrations by support vector machines and neural networks using principal component analysis[J]. Simulation Modelling Practice and Theory, 2008, 16: 1488-1502.

[10] Balaguer E, Palomares A, Soria E, et al. Predicting service request in support centers based on nonlinear dynamics, ARMA modeling and neural networks[J]. Expert Systems with Applications, 2008, 34: 665-672.

[11] LIU Long-mu, Bhattacharyya S, Sclove S L, et al. Data mining on time series: An illustration using fast-food restaurant franchise data[J]. Computational Statistics & Data Analysis, 2001, 37: 455-476.

[12] More A, Deo M C. Forecasting wind with neural networks[J]. Marine Structures, 2003, 16: 35-49.

[13] Alonso A M, Berrendero J R, Hernandez A, et al. Time series clustering based on forecast densities[J]. Computational Statistics & Data Analysis, 2006, 51: 762-776.

[14] 杨叔子, 吴雅, 轩建平, 等. 时间序列分析的工程应用[M]. 武汉: 华中科技大学出版社, 2007: 175-311.
YANG Shu-zi, WU Ya, XUAN Jian-ping, et al. Time series analysis in engineering application[M]. Wuhan: Huazhong University of Science & Technology Press, 2007: 175-311.

[15] 丛爱岩, 成枢, 刘春. 时序分析法在岩层与地表移动中的应用[J]. 中国矿业大学学报, 1999, 28(2): 159-161.
CONG Ai-yan, CHENG Shu, LIU Chun. Application of time series analysis to strata and ground movement[J]. Journal of China University of Mining & Technology, 1999, 28(2): 159-161.

[16] 杨永国, 秦勇. 煤层气产能预测随机动态模型及应用研究[J]. 煤炭学报, 2001, 26(2): 122-125.
YANG Yong-guo, QIN Yong. Study and application on random dynamic model of the coalbed methane output forecasting[J]. Journal of China Coal Society, 2001, 26(2): 122-125.

[17] 刘晓菲. 冲击地压电磁辐射前兆信息的时间序列数据挖掘及群体识别体系研究[D]. 徐州: 中国矿业大学安全工程学院, 2008: 96-134.
LIU Xiao-fei. Study on time series data mining and group recognition system of electromagnetic precursor information of rock burst[D]. Xuzhou: China University of Mining & Technology. School of Safety Engineering,, 2008: 96-134.

(编辑 陈灿华)

收稿日期：2011-06-05；修回日期：2011-08-02

基金项目：国家重点基础研究发展规划(”973”计划)项目(2010CB732004)；中南大学研究生学位论文基金资助项目(2009ssxt231)

通信作者：赵国彦(1963-)，男，湖南沅江人，博士，教授，从事采矿、岩石力学、矿山通风与环保、安全技术等方面的教学与研究；电话：0731-88879612；E-mail：gy.zhao@263.net