小冲杆试验法评价大块非晶合金的超塑性性能

张志豪, 谢建新

(北京科技大学 材料科学与工程学院, 北京 100083)

摘 要: 采用小冲杆试验法(SPT)研究了大块非晶合金(Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5)在不同温度和不同压头速度下的变形行为, 通过SPT载荷—位移曲线结合理论分析, 确定大块非晶(BMG)材料超塑性本构关系。 结果表明, BMG材料的SPT载荷—位移曲线对压头速度和实验温度的敏感性较高, 而SPT载荷—位移曲线的形状与材料的应变速率敏感系数、 粘度、 压头速度等因素有关。 在应变速率敏感系数和压头速度固定的条件下, SPT最大破裂载荷与粘度成正比; 最大破裂位移仅随应变速率敏感系数的增大而增大, 而与压头速度和粘度的大小无关。 获得了Zr_41.25Ti_13.75Ni₁₀Cu_12.5Be_22.5 BMG应变速率敏感系数和表观粘度, 确定了该合金的超塑性本构关系。

关键词: 小冲杆试验; 大块非晶合金; 超塑性; 本构关系 中图分类号: TB302.5

文献标识码: A

Super-plasticity of bulk metallic glass evaluated by small punch test

ZHANG Zhi-hao, XIE Jian-xin

(School of Materials Science and Engineering,University of Science and Technology Beijing, Beijing 100083)

Abstract: The deforming behaviors of Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 bulk metallic glass(BMG) under different temperatures and punch velocities were investigated by the small punch test. Based on SPT load—displacement curves and combined with theoretical analysis, a method for determining super-plastic constitutive relations of BMG was proposed. The results show that the SPT load—displacement curves of BMG are very sensitive to punch velocity and test temperature, and the shape of SPT load—displacement curves is controlled by strain rate sensitivity, viscosity and punch velocity etc. When the strain rate sensitivity and punch velocity are certain, maximal crack loads of SPT load—displacement curves are proportional to viscosities. Maximal crack displacement increases with the increase of strain rate sensitivity, and is independent on punch velocity and viscosity. The strain rate sensitivities and viscosities of Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 BMG under different test conditions are obtained, and the super-plastic constitutive relations of the alloy are determined.

Key words: small punch test; bulk metallic glass; super-plasticity; constitutive relation

   由于大块非晶合金(BMG)在过冷区域表现出良好的超塑性性能, 因而有望通过塑性加工方法来制造非晶质的复杂结构精细零部件, 促进BMG材料的广泛应用^{[1, 2]}。 为了确定BMG合理的超塑性成形温度、 应变速率等工艺参数, 需要通过大量拉伸或压缩实验来研究合金在不同温度和应变速率下的力学性能。 由于BMG材料在常温下具有很高的强度和硬度, 给常规拉伸或压缩试样的制备带来较大困难。 小冲杆试验法(SPT)所需要的试样尺寸很小, 且形状规则(一般为圆片状或矩形片状), 能最大限度地克服上述不利之处。 同时, 采用小试样也有利于减少实验成本。

SPT法为采用小冲杆以一定速度顶压薄片状试样, 通过记录冲杆的载荷—位移曲线, 分析计算材料各种性能参数的一种材料评价方法。 此种方法起源于受辐射材料性能的评定, 经过20多年的发展, 已经在合金钢、 复合材料和无机材料的塑性、 韧性、 蠕变行为及断裂强度等的表征方面取得了一定的研究进展^[3-6]。 但由于SPT中试样应力分布的复杂性, 使得这方面的工作多处于实验室研究阶段, 没有大规模应用到工程实践中去。 本文作者结合大块非晶合金超塑性性能的评价, 研究以SPT实验载荷—位移曲线为基础, 通过理论辅助分析, 确定合金的超塑性本构关系的方法。

1 小冲杆试验法的基本原理

典型的SPT载荷—位移曲线如图1所示^[7]。 Okada等^[8] 将图1所示的曲线分为弹性变形(图中Ⅰ区)、 塑性弯曲变形(图中Ⅱ区)、 薄板伸张(图中Ⅲ区)和破裂(图中Ⅳ区)4个阶段。 当塑性弯曲变形阶段结束时, 所对应的塑性弯曲位移与塑性弯曲载荷最大; 薄板伸张变形阶段结束时所对应的破裂位移与破裂载荷最大。

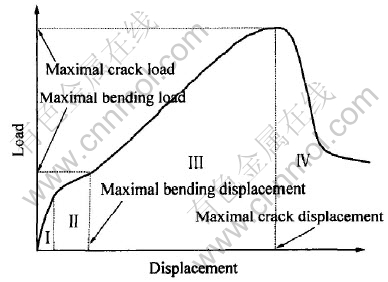
图1   小冲杆试验典型载荷和位移的变化曲线

Fig.1   Chang curves of load and displacement for SPT

本研究所采用的SPT装置如图2所示。 实验模具主要尺寸是以文献[9]为主要参考而确定的, 其中小冲杆下端半球部直径为2.6mm, 上模孔直径为5.5mm, 下模孔直径为4.6mm, 下模孔倒圆半径为0.2mm。 小冲杆的上压头与MTS材料试验

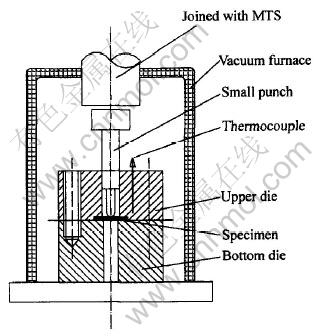
图2   小冲杆试验装置示意图

Fig.2   Abbreviated drawing of SPT apparatus

机相连, 实验过程中的载荷—位移曲线数据由计算机自动采集。

2 结果与分析

将直径为8mm的Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 BMG棒材线切割成厚度为0.6^+0.02mm的圆片状试样, 端面打磨并抛光至镜面。 实验过程中的压头速度为5~50μm/s, 温度为360~390℃, 升温速度为20℃/min, 真空度小于1Pa。

图3所示为不同压头速度下Zr_41.2Ti_13.8Cu_12.5-Ni₁₀Be_22.5在390℃时的SPT载荷—位移曲线。 由图3可知, 随着压头速度的降低, 最大塑性弯曲载荷与最大破裂载荷随之下降, 而塑性弯曲变形阶段的位移却随之增加。

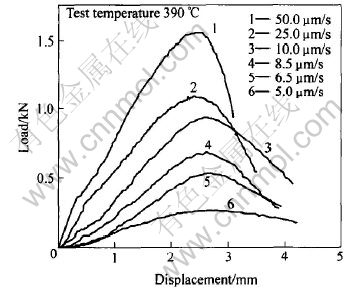
图3   不同压头速度下Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5小冲杆试实验的载荷—位移曲线

Fig.3   Change curves of load and displacement for Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 under different punch velocity by SPT

图4所示为Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5在不同温度下的载荷—位移曲线。 由图4可知, 在合金的过冷温度区域内(362.6~437.4℃^[10]), 随着实验温度的提高, 载荷—位移曲线中的最大塑性弯曲载荷与最大破裂载荷也随之下降, 而塑性弯曲变形阶段的位移却随之增加。

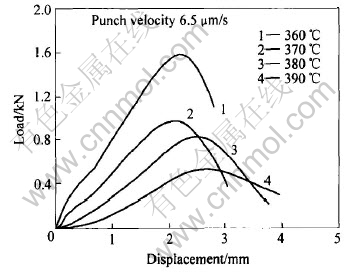
图4   不同温度下Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5小冲杆实验的载荷—位移曲线

Fig.4   Change curves of load and displacement for Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 at different temperatures by SPT

本文作者采用传统SPT破裂载荷的概念来定义图3和4中的最大载荷。 而实际上, 较高实验温度下的BMG试样在到达最大载荷后并没有立即产生裂纹, 而是首先产生显著的局部变薄现象, 然后才开始破裂。 从图3和4中可以看出, Zr基BMG材料的SPT载荷—位移曲线对压头速度和实验温度十分敏感, 当压头速度变化量为1.5μm/s、 实验温度变化量为10℃时, 实验载荷—位移曲线即表现出十分明显的变化。 因此, 通过SPT来评价类似BMG的大应变速率敏感系数或对温度很敏感的材料的力学性能是完全可行的。

另一方面, Zr基BMG材料在其过冷温度区域的超塑性本构方程的数学模型可假设为^[11]

式中 σ为 流动应力; η为表观粘度;为应变速率; m为应变速率敏感系数。

由于SPT实验获得的数据是载荷—位移曲线, 并不能直接获得反映材料超塑性性能的特征指标, 如式(1)中的η和m。 故本研究拟采用有限元辅助计算分析的方法, 寻求从SPT的载荷—位移曲线确定超塑性材料特征指标(本构方程)的途径。

3 小冲杆试验过程的有限元分析

根据SPT装置的结构特点、 载荷及边界条件的对称性, 采用轴对称分析模型, 并取其一半进行分析。 有限元分析模型如图5所示, 将实验坯料分为(40×6)个四边形网格, 上模、 下模及压头设为刚体, 压头以一定的速度垂直向下运动。 由于大块非晶合金在超塑性成形时呈现出比一般金属材料更大的摩擦阻力^[12], 考虑到实验在无润滑状态下进行, 试样与模具之间的接触摩擦因数取0.4。

采用MARC有限元软件进行分析。 通过改变压头速度、 表观粘度和应变速率敏感系数, 可以获得不同形状的小冲杆载荷—位移计算曲线。 通过进一步的有限元分析, 可以得出最大破裂位移与应变速率敏感系数的关系曲线, 结果如图6所示。 图6所示的关系仅与实验装置所使用的模具尺寸及试样尺寸相关, 因此也同样适用于塑性本构关系满足式(1)的其它超塑性材料。 由图6可看出, 最大破裂位移仅随应变速率敏感系数的增大而增大, 与压头速度和粘度无关。 由此可以通过SPT法所直接获得的最大破裂位移值来确定超塑性材料的应变速率敏感系数。

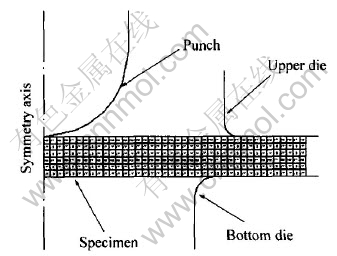
图5   小冲杆试验的有限元分析模型

Fig.5   Finite element model of small punch test

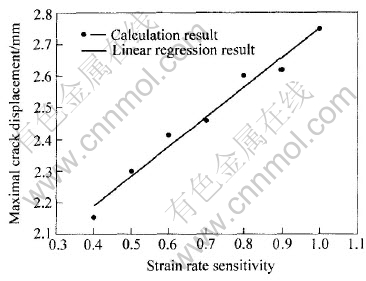
图6   最大破裂位移与应变速率敏感系数的关系曲线(FEM计算结果)

Fig.6   Curve of maximal crack displacement vs strain rate sensitivity (results calculated by FEM)

对超塑性材料而言, 在实验温度、 压头速度、 模具尺寸和坯料尺寸一定的条件下, SPT所获得的载荷—位移曲线应是唯一的。 因此, 在其它条件固定不变的前提下, 通过有限元计算可以获得最大破裂载荷在不同粘度条件下随应变速率敏感系数变化的曲线, 结果如图7所示。 此外, 有限元计算结果也表明, 在应变速率敏感系数和压头速度固定的条件下, SPT载荷—位移曲线的最大破裂载荷与实验材料的粘度成正比, 所以在已知材料的应变速率敏感系数的前提下, 通过图7可以确定材料在某一应变速率敏感系数下的粘度。

综上所述, 对某一超塑性材料, 在本研究的小冲杆实验模具及试样尺寸条件下, 由以一定的压头速度获得的SPT载荷—位移曲线可确定最大破裂位移和最大破裂载荷, 然后由图6可确定材料的应变速率敏感系数, 再由图7确定材料的表观粘度, 最后由式(1)可以确定材料的超塑性本构方程。

4 误差分析

参考Chakrabarty^[13]和Wang^[14]的研究, 建立了SPT变形的几何模型(见图8)。 图中的u为可变形区半径, R为冲杆半径, r为已变形区半径, z为某个微小单元与薄板初始位置的距离, 而φ是微小单元法线与垂直轴的夹角, β为接触边界与垂直轴的夹角。

Chakrabarty给出了压头位移H与θ和β的关系式^[12]:

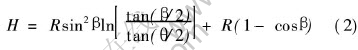
θ和β的关系式为

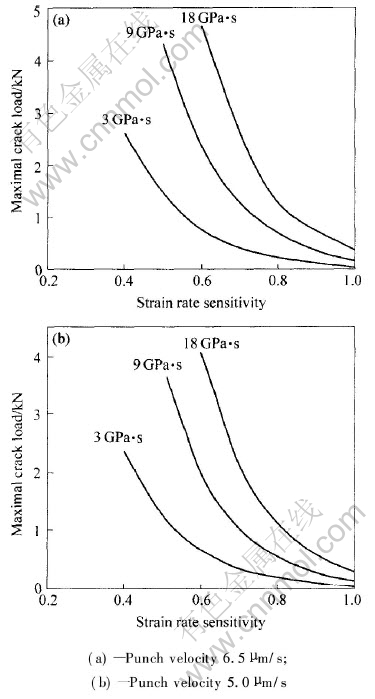
图7   粘度对最大破裂载荷—应变速率敏感系数关系曲线的影响(FEM计算结果)

Fig.7   Effect of viscosities on maximal crack load vs strain rate sensitivity curves (results calculated by FEM)

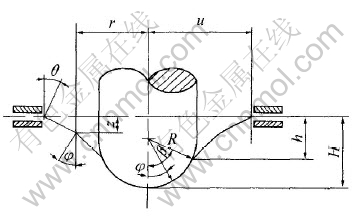
图8   小冲杆试验的几何模型

Fig.8   Geometry model of SPT

接触边界上板料的应变由下式确定:

根据本研究所采用的小冲杆实验条件, 取R=1.3mm、 u=2.3mm, 同时设β在0~90°之间变化, 由式(3)求出相应的θ后, 可以由式(2)和(4)分别求出相应的H和ε, 对计算结果进行回归, 可以得出平均应变与压头位移的关系:

ε=0.0942H²+0.1551H(5)

若小冲杆试验的压头速度为v、 冲压时间为t, 将式(5)等号两边对时间求导数, 可得出某一时刻压头与坯料接触边界上的应变速率与压头速度的关系:

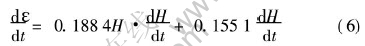
即

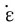=0.1884H·v+0.1551v(7)

由于在小冲杆试验过程中, 板料经过弹性变形、 塑性弯曲位移之后, 才进入薄膜伸张阶段, 而Chakrabarty给出的公式是针对薄膜伸张阶段, 所以利用上式计算应变速率时必须使压头位移H大于最大塑性弯曲位移。

从式(7)可以看出, 在压头速度一定的条件下, 小冲杆试验板料的平均应变速率并不是固定不变的, 而是随压头位移H的增大而增大。 文献[15]表明, BMG材料在过冷温度区域内的流动模式将随应变速率的提高而逐渐从均匀流动模式发展为非均匀流动模式, 即应变速率敏感系数将随应变速率的提高而减小; 同时粘度也随应变速率的增大而减小。 因此, 采用小冲杆试验有限元分析时所选用的超塑性本构方程中的应变速率敏感系数也随压头位移的增大而减小, 同时粘度也随之减小。 而上述有限元分析时并没有考虑这一因素, 因此, 通过图6和7确定应变速率敏感系数和粘度时会产生一定误差。

在上述有限元分析过程中, 假设材料在变形过程中不发生破裂, 即没有考虑到裂纹扩展对最大破裂载荷的影响, 而Zr_41.25Ti_13.75Ni₁₀Cu_12.5Be_22.5BMG的小冲杆试验在载荷为最大破裂载荷的20%左右时停止实验, 发现380℃、 6.5μm/s和390℃、 小于25μm/s的试样都没有宏观裂纹, 此时采用上述假设是合理的。 但360℃、 6.5μm/s, 370℃、 6.5μm/s和390℃、 50μm/s的试样出现明显裂纹扩展, 此时采用上述假设将会带来较大的误差, 由于这些条件下的小冲杆载荷—位移曲线给出的载荷值因裂纹的产生和扩展而必定小于理论模拟的数值所致。

5 应用举例

由Zr_41.25Ti_13.75Ni₁₀Cu_12.5Be_22.5 BMG在不同实验条件下小冲杆载荷—位移曲线, 根据图6和7可以确定所对应的应变速率敏感系数和粘度, 实验条件和计算结果如表1所列。

由式(7)可以确定在给定压头速度和压头位移

表1   不同实验条件下SPT载荷—位移曲线特征值及BMG超塑性本构方程

Table 1   Characteristic values of SPT load—displacement curves and superplastic constitutive equations

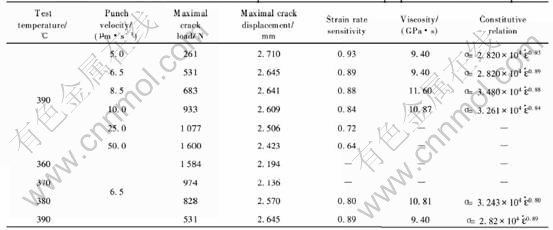
下的接触边界应变速率, 结合表1可以得到Zr_41.25Ti_13.75Ni₁₀Cu_12.5Be_22.5材料在390℃时的应变速率敏感系数随试样接触边界处的应变速率的变化曲线(见图9)。 由于小冲杆试验从最大塑性弯曲位移到最大破裂位移时接触边界上试样的应变速率是变化的, 为了便于比较, 图9中的应变速率值统一取压头位移为1.5mm时所对应的应变速率。 从图9可看出, 在较小的应变速率范围内, 小冲杆试验与理论分析相结合所确定的应变速率敏感系数与文献报道的实验结果十分接近。

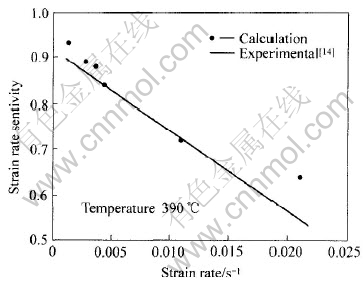
图9   Zr_41.25Ti_13.75Ni₁₀Cu_12.5Be_22.5应变速率敏感系数与应变速率的关系

Fig.9   Relationship between strain rate sensitivity and strain rate

6 结论

1) 提出了一种由SPT载荷—位移曲线结合理论分析来评价材料超塑性性能的方法, 并对此方法在实际应用过程中可能出现的误差进行了分析。

2) SPT的载荷—位移曲线的形状与材料的应变速率敏感系数、 粘度、 压头速度等因素有关。 在应变速率敏感系数和压头速度一定的条件下, 最大破裂载荷与粘度成正比; 而最大破裂位移仅随应变速率敏感系数的增大而增大, 与压头速度和粘度的大小无关。

3) 以Zr_41.2Ti_13.8Cu_12.5Ni₁₀Be_22.5 BMG材料为试样的研究结果表明, 采用 SPT法来评价大块非晶合金材料的应变速率敏感系数和粘度是完全可行的。

4) 通过小冲杆试验, 获得了Zr_41.25Ti_13.75Ni₁₀-Cu_12.5Be_22.5大块非晶合金的应变速率敏感系数和表观粘度, 在较低的应变速率范围内, 本研究的应变速率敏感系数与文献报道的实验数据相符合。

REFERENCES

[1]张志豪, 刘新华, 谢建新. Zr基非晶合金精密直齿轮超塑性成形实验研究[J]. 机械工程学报, 2005, 41(3): 151-154.

ZHANG Zhi-hao, LIU Xin-hua, XIE Jian-xin. Super-plastic die forging of fine precision spur gear of Zr-based bulk metallic glass[J]. Chinese Journal of Mechanical Engineering, 2005, 41(3): 151-154.

[2]谢建新, 周成, 张志豪. 非晶合金精细零部件的超塑性成形技术[J]. 材料导报, 2003, 17(2): 8-11.

XIE Jian-xin, ZHOU Cheng, ZHANG Zhi-hao. Superplastic forming techniques for fine precision amorphous alloy parts[J]. Materials Review, 2003, 17(2): 8-11.

[3]Ha J S, Fleury E. Small punch test to estimate the mechanical properties of steels for steam power plant (Ⅱ): fracture toughness[J]. International Journal of Pressure Vessels and Piping, 1998, 75(9): 707-713.

[4]Cheon J S, Kim I S. Evaluation of thermal aging embrittlement in CF8 duplex stainless steel by small punch test[J]. Journal of Nuclear Materials, 2000, 278(1): 96-103.

[5]江莞, 王刚, 吴历斌, 等. MSP试验法评价Mo/PSZ系复合材料的强度特性[J]. 无机材料学报, 2002, 17(4): 827-832.

JIANG Wan, WANG Gang, WU Li-bin, et al. High temperature strength of Mo/PSZ composites evaluated by MSP test[J]. Journal of Inorganic Materials, 2002, 17(4): 827-832.

[6]Yang Z, Wang Z W. Relationship between strain and central deflection in small punch creep specimens[J]. International Journal of Pressure Vessels and Piping, 2003, 80(6): 397-404.

[7]Ruan Y, Spatig P, Victoria M. Assessment of mechanical properties of the martensitic steel EUROFER97 by means of punch tests[J]. Journal of Nuclear Materials, 2002, 307-311(1): 236-239.

[8]Okada A, Lucas G E, Kiritani M. Micro-bulge test and its application to neutron-irradiated metals[J]. Transactions of the Japan Institute of Metals, 1988, 29(1): 99-108.

[9]Martin A, Meinhard K. Determination of deformation and failure properties of ductile materials by means of the small punch test and neural networks[J]. Computational Materials Science, 2003, 28(3-4): 633-644.

[10]张志豪, 刘新华, 周成, 等. Zr基大块非晶合金的超塑性成形性能[J]. 中国有色金属学报, 2004, 14(7): 1073-1077.

ZHANG Zhi-hao, LIU Xin-hua, ZHOU Cheng, et al. Super-plastic forming properties of Zr-based bulk amorphous alloys[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(7): 1073-1077.

[11]Inoue A, Kawamura Y, Shibata T, et al. Viscous flow deformation in supercooled liquid state of bulk amorphous Zr₅₅Al₁₀Ni₅Cu₃₀ alloy[J]. Materials Tran-sactions JIM, 1996, 39 (6): 1337-1341.

[12]张志豪, 周成, 谢建新. Zr₅₅Al₁₀Ni₅Cu₃₀大块非晶合金的超塑性挤压成形性能[J]. 中国有色金属学报, 2005, 15(1): 33-37.

ZHANG Zhi-hao, ZHOU Cheng, XIE Jian-xin. Superplastic extrusion behavior of Zr₅₅Al₁₀Ni₅Cu₃₀ bulk metallic glass[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(1): 33-37.

[13]Chakrabarty J. A theory of stretch forming over hemis pherical punch heads[J]. International Journal of Mechanical Sciences, 1970, 12(7): 314-325.

[14]Wang N M. Large plastic deformation of a circular sheet caused by punch stretching[J]. Journal of Applied Mechanics, 1970, 37(6): 431-439.

[15]Johnson W L, Lu J, Demetriou M D. Deformation and flow in bulk metallic glasses and deeply undercooled glass forming liquid—a self consistent dynamic free volume model[J]. Intermetallics, 2002, 10(10): 1039-1044.

(编辑李艳红)

基金项目: 国家杰出青年科学基金资助项目(50125415); 北京市科技计划重大资助项目(H020420030320)

收稿日期: 2005-07-15; 修订日期: 2005-08-20

作者简介: 张志豪(1970-), 男, 博士研究生

通讯作者: 谢建新, 男, 教授, 博士; 电话: 010-62332309; 传真: 010-62327283; E-mail: jxxie@mater.ustb.edu.cn