分形在砂状氧化铝强度研究中的应用
谭 军, 陈启元, 尹周澜, 张平民, 李 洁
(中南大学 化学化工学院, 湖南 长沙, 410083)
摘要: 应用分形理论研究了砂状氧化铝表面形貌和强度的关系。 采用扫描电镜分析了一系列种分、 碳分氧化铝颗粒的形貌特征, 进行了分维数的计算和磨损指数的测定。 研究结果表明, 碳分氧化铝的磨损指数随分维数增大而增大; 种分氧化铝磨损指数和分维数之间的关系必须结合形貌结构进行分析, 形貌结构类型相同的种分氧化铝的磨损指数随分维数增大而增大。
关键词: 分形; 砂状氧化铝; 显微结构; 磨损指数; 强度
中图分类号:TF821 文献标识码:A 文章编号: 1672-7207(2005)05-0833-04
Application of fractal theory to studying strength of sandy alumina
TAN Jun, CHEN Qi-yuan, YIN Zhou-lan, ZHANG Ping-min, LI Jie
(School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China)
Abstract: The fractal theory was introduced to study the relationship between sandy alumina morphology and strength. Morphological characterizations of a series of alumina from seeded and carbonization precipitation were described using scanning electron microscopy (SEM). Attrition indices and fractal dimensions were determined. The results show that the attrition index of alumina from carbonization precipitation increases with the increase of fractal dimension. The crystal structure should be considered during analyzing the relationship between fractal dimension and strength. The attrition index of alumina with the same structure increases with the increase of fractal dimension.
Key words: fractal dimension; sandy alumina; microstructure; attrition index; strength
随着中间下料大型预焙电解槽的广泛使用, 砂状氧化铝的生产已经成为必然趋势。 与粉状氧化铝相比, 砂状氧化铝的物理性能特别是粒度分布和强度两项指标有明显改善[1]。 从生产中间状或者粉状氧化铝向砂状氧化铝的转型过程中, 如何提高氧化铝强度一直是亟待解决的技术难题。
物质性能由其结构决定, 通过扫描电子显微镜分析, 可以获得氢氧化铝、 氧化铝结构及形貌等信息, 但目前对颗粒形貌特征的描述大多处于定性阶段[2-4]。 为量化颗粒表面形貌, 一些图形分析理论给人们提供了新的研究方法, D.W.Lurkens等[5]认为对颗粒的轮廓曲线进行傅里叶变换, 可以获得表征颗粒几何特征的傅里叶系数, K.Belaroui等[6, 7]通过摄取氢氧化铝的扫描电镜形貌, 采用一定的图形分析方法计算了颗粒的形状描述因子。 近年来, 分形理论也不失为一种较好的研究方法[8]。
Mandelbrot[9]分形理论认为, 自然界中大多数物体具有复杂、 不光滑和不规则的特征, 这些复杂的对象在其局部和整体之间存在着自相似性, 可以用分维数进行描述。 分维数的测定方法很多, 盒子维法是常用方法之一, 盒维数表征了形貌灰度表面纹理粗糙度。 多项研究结果表明, 固体颗粒在分子水平上都可以看作是分形[10]。 王延吉等[11]应用分形理论研究了硫化物催化剂的表面性质及其与合成甲醇反应性能的关系。 目前尚未见用分形维数关联研究具有分形特征[12]的氧化铝的强度的报道。
在此, 作者采用扫描电镜摄取氧化铝颗粒的表面形貌, 测定氧化铝的分维数, 并且分析氧化铝强度和表面形貌之间的定量关系。
1 实 验
实验原料为按不同工艺制备的一系列的种分和碳分砂状氧化铝。
砂状氧化铝强度通常用磨损指数(I)表征, 其测定参照中国有色金属行业标准[13], 氧化铝颗粒在磨损指数仪中被一定分压和分量的气流吹动循环15 min后, 分析其粒度分布, 按式(1)计算磨损指数:
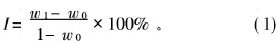
式中: w0和w1分别为磨损前、 后样品粒度小于45 μm的氧化铝颗粒的质量分数。
用JSM-5600LV型扫描电镜观察氧化铝颗粒的形貌。
分形维数的测定采用盒维数法, 将扫描电镜摄取的氧化铝颗粒的形貌图像压缩成64×64的图像, 并将图像灰度级定为64作为第三维信息, 建立64×64×64的立方体, 统计覆盖的盒子数和每个盒子所含灰度的级数, 按式(2)计算分维数Df[14]。 其中, Bij为代盒子所含灰度的级数。
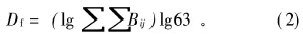
2 结果与分析
工业生产电解用氧化铝通常采用铝酸钠溶液种分或者碳分的方法制备, 工艺条件的不同使种分氧化铝和碳分氧化铝的形貌特征有差异, 从而对强度的影响不同。
2.1 碳分氧化铝分维数和强度的关系
碳分工艺所获得的氧化铝的扫描电镜形貌如图1所示。 由图1可知, 组成碳分氧化铝颗粒的小晶粒呈六角柱状, 表面极度不规则, 具有分形特征。 对一系列碳分氧化铝样品进行磨损指数测定、 扫描电镜形貌摄取和分维数的计算。 样品的分维数和磨损指数关系图如图2所示。 由图2可见, 碳分氧化铝磨损指数随分维数增大而增大。 根据摩擦学理论[15], 表面粗糙度影响磨损, 颗粒在抵抗切向运动时, 粗糙度大的地方易产生形变和切变, 分维数越大, 说明颗粒表面粗糙度越大, 越易磨损。 此外, 不同分维数变化区间, 磨损指数变化幅度不同, 当分维数从1.9变化至1.92时, 磨损指数从5.3变化至9; 而分维数从1.92变化至1.94时, 磨损指数从9变化至30, 说明分维数小于1.92与大于1.92的氧化铝的磨损机理不同。 结合磨损后颗粒的显微形貌(如图3所示)进行分析, 分维数比较小的[CM(22] 氧化铝, 磨损后颗粒表面只出现一定程度的磨蚀,

图 1 碳分氧化铝SEM形貌
Fig. 1 SEM image of alumina from carbonization precipitation
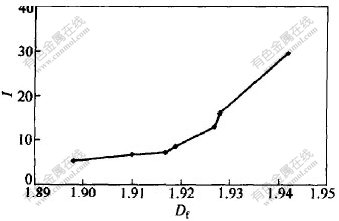
图 2 碳分氧化铝分维数Df与磨损指数I关系图
Fig. 2 Relationship between fractal dimension and attrition index of alumina from carbonization precipitation
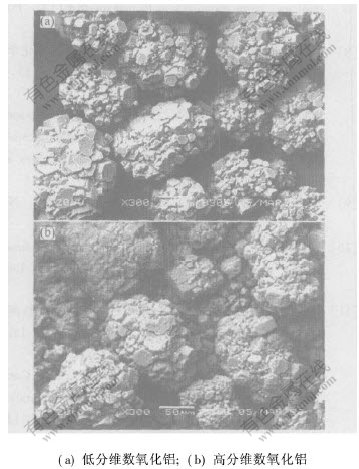
图 3 磨损后碳分氧化铝SEM形貌
Fig. 3 SEM images of alumina from carbonization precipitation after attrition experiments
因此其磨损指数低; 分维数较大的颗粒, 除了表面被磨蚀外, 有小晶块从大颗粒脱落, 使磨损指数升高。
2.2 种分氧化铝分维数和强度的关系
种分氧化铝的典型扫描电镜形貌如图4所示, 组成种分氧化铝颗粒的小晶粒呈六角棱柱状。 对一系列种分氧化铝样品进行磨损指数的测定和分维数的计算, 两者之间的关系如图5所示, 从图5可见,

图 4 种分氧化铝形SEM形貌
Fig. 4 SEM image of alumina from seeded precipitation
磨损指数与分维数之间不呈单调变化趋势, 这是不同种分工艺条件使产品氧化铝形貌结构相差很大所致。 根据磨损指数将图5分成3个区间(〈20, 20~30, >30), 可以发现在每个区间内, 磨损指数随分维数增大而增大。 从氧化铝形貌结构分析可知, 磨损指数小于20的主要是镶嵌型氧化铝, 大于30的主要是径向长大型氧化铝, 混合型氧化铝的磨损指数介于两者之间。 结合磨损后氧化铝的显微结构 (如图6所示)分析, 镶嵌型氧化铝磨损后颗粒表面只出现一定程度的磨蚀, 而其他类型氧化铝除表面磨损外, 颗粒出现不同程度的破裂现象, 说明种分氧化铝强度除受表面粗糙度影响外, 晶体内部结构是重要影响因素。 因此, 对种分氧化铝, 必须结合显微结构进行分析, 才能预测其磨损指数的大小。
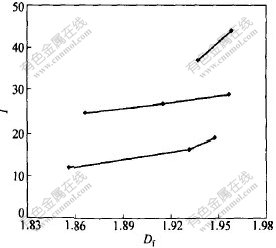
图 5 种分氧化铝分维数Df与磨损指数I的关系
Fig. 5 Relationship between fractal dimension and attrition index of alumina from seeded precipitation

图 6 磨损后种分氧化铝SEM形貌
Fig. 6 SEM images of alumina from seeded precipitation after attrition experiments
3 结 论
运用分形理论在一定程度上可以定量研究氧化铝磨损指数和形貌的关系; 碳分氧化铝的磨损指数随分维数增大而增大; 必须结合形貌结构对种分氧化铝磨损指数和分维数之间的关系进行分析, 形貌结构类型相同的种分氧化铝的磨损指数随分维数增大而增大。
参考文献:
[1]杨重愚. 氧化铝生产工艺学[M]. 北京: 冶金工业出版社, 1993.
YANG Zhong-yu. Technology of Alumina Production[M]. Beijing: Metallurgy Industry Press, 1993.
[2]Sweegers C, de Coninck H C, Meekes H, et al. Morphology, evolution and other characteristics of gibbsite crystals grown from pure and impure aqueous sodium aluminate solutions[J]. Journal of Crystal Growth, 2001, 233(3): 567-582.
[3]Isabelle S, Stephane V, Gerard P, et al. The influence of additives on the crystal habit of gibbsite[J]. Journal of Crystal Growth, 1999, 196(1): 174-180.
[4]Addai-mensah J. Surface and structural characteristics of gibbsite precipitated from pure, synthetic Bayer liquor[J]. Minerals Engineering, 1997, 10(1): 81-96.
[5]Luerkens D W, Beddow J K, Vetter A F. Morphological Fourier descriptors[J]. Powder Technology, 1982, 31(2): 209-215.
[6]Belaroui K, Pons M N, Vivier H. Morphological characterization of gibbsite and alumina[J]. Powder Technology, 2002, 127(3): 246-256.
[7]Pons M N, Vivier H, Belaroui K, et al. Particle morphology: from visualization to measurement[J]. Powder Technology, 1999, 103(1): 44-57.
[8]郭从容, 杨桂琴, 王雪松, 等. 分形理论及其在化学和化工中的应用[J]. 化学工业与工程, 1999, 16(1): 33-38.
GUO Cong-rong, YANG Gui-qin, WANG Xue-song, et al. The fractal theory and its application in chemistry and chemical engineering[J]. Chemical Industry and Engineering, 1999, 16(1): 33-38.
[9]Mandelbrot. Fractal Geometry of Nature[M]. New York: W H Freeman, 1982.
[10]Pfeifer P, Avnir D. Chemistry in noninteger dimensions between two and three[J]. J Chem Phy, 1983, 79(7): 3558-3565.
[11]王延吉, 张继炎, 张鎏. 硫化物催化剂结构性质与合成甲醇反应性能的关联(Ⅱ)[J]. 化工学报, 1998, 49(3): 329-335.
WANG Yan-ji, ZHANG Ji-yan, ZHANG Liu. Correlation of the structural properties of sulfide catalysts with their reactivity for methanol synthesis(Ⅱ)[J]. Chemical Engineering Transactions, 1998, 49(3): 329-335.
[12]李洁, 陈启元, 王龙章, 等. 铝酸钠溶液种分反应界面分维数的估算[J]. 中国稀土学报, 1998, 16(专辑): 605-609.
LI Jie, CHEN Qi-yuan, WANG Long-zhang, et al. A fractal dimension study on the reaction surface of seeded caustic aluminate solution [J]. Journal of Rare Earths, 1998, 16(S): 605-609.
[13]YS/T 438. 2—2001. 砂状氧化铝物理性能测定方法——磨损指数的测定[S].
YS/T 438. 2—2001. Methods for Physical Performance Determination of Sandy Alumina——Determination of the Attrition Index[S].
[14]张济忠. 分形[M]. 北京: 清华大学出版社, 1995.
ZHANG Ji-zhong. Fractal Dimension[M]. Beijing: Tsinghua University Press, 1995.
[15]Sacal A D. 金属的磨损[M]. 董阳照, 译. 石家庄: 河北人民出版社, 1982.
Sacal A D. Wear of Metals[M]. DONG Yang-zhao, translates. Shijiazhuang: Hebei People Press, 1982.
收稿日期:2004-12-15
基金项目: 国家重大基础研究发展规划资助项目(G19990649); 国家“十五”科技攻关资助项目(2001BA609A—18); 国家自然科学基金资助项目(50374097)
作者简介:谭 军(1971-), 女, 湖南长沙人, 讲师, 博士研究生, 从事冶金及应用物理化学研究
论文联系人: 谭 军, 女, 讲师, 博士研究生; 电话: 0731-8877364(O); E-mail: yytanjun@163.com