Trans. Nonferrous Met. Soc. China 31(2021) 297-305

Numerical simulation of liquid aluminum leakage in casting process

Ling-yu KONG¹, Xiao-zhen LIU¹, Zhong-ning SHI², Tuo-fu LI¹, Zhao-wen WANG¹, Ai-min LIU¹

1. Key Laboratory for Ecological Metallurgy of Multimetallic Mineral (Ministry of Education), Northeastern University, Shenyang 110819, China;

2. State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110819, China

Received 29 February 2020; accepted 6 August 2020

Abstract: A model was built to simulate liquid aluminum leakage during the casting process, including transient trough flow, orifice outflow, and spread, to prevent the explosion. A comparison between the simulation data and the theoretical calculation results verifies that the model has remarkable adaptability and high accuracy. Although the height of liquid aluminum in the mixing furnace and outlet radius are changed, the molten aluminum will not leak during the casting process. The aluminum in the trough moves forward in a wave-like motion and causes a leakage. The spread of the leaked aluminum resembles a long strip on the ground. The leakage amount and spread area of liquid aluminum increase with increasing the height of liquid aluminum in the mixing furnace.

Key words: liquid aluminum leakage; explosion; leakage state; spread pattern; numerical simulation; volume of fluid (VOF) model

1 Introduction

Molten metals are used for forging ingots, such as aluminum and aluminum alloys [1]. Explosions can occur when a high-temperature molten metal contacts an evaporable and cryogenic liquid, such as water [2]. According to data collected by the Aluminum Industry Association, there were 1877 explosions of molten metals from 1980 to 2002, of which 614 occurred during the casting process [3]. Hence, preventing explosions caused by the contact of molten metal with water is critical to the metal casting process.

The casting process of liquid aluminum is shown in Fig. 1. The aluminum produced by an electrolytic cell is poured into a mixing furnace for homogenization. The liquid aluminum flows into troughs from the mixing furnace outlet, and the high-temperature molten aluminum is transported through the troughs to each casting mold on the conveyor. The liquid aluminum in the mold is cooled to become an aluminum ingot. Due to the existence of a sprinkling cooling zone, water is distributed on the ground of the casting workshop. If molten aluminum leaks and contacts the water, there is a risk of explosion.

At present, many researchers have investigated the problem of explosions caused by the contact between molten metals and water, and they mainly focus on the explosion mechanism and explosion effects [4-7]. LIU et al [8] experimentally studied the explosion mechanism between high-temperature molten aluminum and water by changing the temperature and contact ratio of aluminum to water. They found that explosions occur when the ratio of aluminum to water is within a certain range. The higher the water temperature is, the less likely an explosion will occur. LOWERY and ROBERTS [9] introduced organic coatings, such as Wise Chem E-212-F that can prevent the explosion of a molten metal; BABAITSEV and KUZNETSOV [10] created a method to predict the blast energy of accidental interactions between molten metal and water, which can calculate the boundaries of the damage zones and provide a basis for the design of explosion-proof building equipment. WOLOSHYN et al [11] abandoned the traditional overpressure assessment method and used a computational fluid dynamics (CFD) modeling method to study the overpressure generated by aluminum-water explosions in a casting workshop. According to the prediction results, this approach can provide a reference for the explosion-proof design of control rooms and other equipment. Unlike other works, this study is focused on the leakage process of liquid aluminum. The CFD modeling method is used to simulate the leakage process, which exhibits advantages of high safety, high accuracy and low cost. The critical conditions of leakage, the leakage pattern of liquid aluminum and its spread form on the ground are also studied. If the leakage state and the spread pattern, as well as the sensitivity of factors affecting the leakage and spread range of liquid aluminum are known, the influence and damage of leakage accidents can be minimized in terms of time and efficiency.

Fig. 1 Liquid aluminum casting process

2 Computational models

2.1 Geometric model

The equipment involved in the start-up phase of the liquid aluminum casting process includes a mixing furnace and troughs, and they are modeled and meshed using ICEM software. The size of the model is based on the industrial equipment of the Taiyuan East Aluminum Co. Ltd., China. The center of the mixing furnace outlet is located in the middle position of the sidewall, which is 0.9 m away from the bottom and 1.3 m away from the side. The global mesh size is set to be 70 mm, and a local refinement of 30 mm is also applied to the mixing furnace outlet and troughs, as shown in Fig. 2.

Fig. 2 Geometric model and mesh

The geometric dimensions and material properties are listed in Table 1. The density of liquid aluminum varies little with temperature, so the density is set as a constant [13]. In metal casting, viscosity is an important rheological parameter for understanding the hydrodynamics and kinetics of reactions [14]. The viscosity of liquid metals is essential to predict the flow of fluid in many metallurgical manufacturing processes [15]. The variable viscosity has a great influence on the flow of liquid aluminum in the casting process and cannot be set as a constant. The viscosity of liquid metals is generally measured by an oscillating viscometer and rotational viscometer [16]. In an oscillating viscometer, the crucible moves along the vertical axis, and liquid metal in the crucible dampens the movement by the absorption and dissipation of the internal friction energy. The viscosity of liquid metals is determined from the decrement and time period of motion [17,18]. A rotational viscometer is used to measure the torque necessary to rotate a spindle immersed in the liquid metal at a constant angular velocity [19].

Table 1 Geometric sizes of model and material properties

MORARU [20], KAPTAY [21] and GAO et al [22] summarized the viscosity formulas for liquid metals and alloys. For liquid aluminum, the viscosity is generally calculated by the Arrhenius formula when the temperature is above the melting point:

η=η₀exp[E/(RT)]                         (1)

where E is the activation energy for viscous flow, η₀ is the pre-exponential viscosity, T is the temperature and R is the gas constant.

MALYSHEV et al [23], SUN et al [24] and BATTEZZATI and GREER [25] used different methods to obtain the formulas for calculating the viscosity of liquid aluminum:

η=1.1603×10^-3(942/T)^1.53091(1049/T)^0.182802        (2)

η=3.101×10^-4exp(1309/T)                 (3)

η=1.49×10^-4exp(1987.29/T)                (4)

where η is the viscosity.

Fig. 3 Comparison of viscosity formulas with handbook of chemistry and physics

Based on Eqs. (2)-(4), temperature-viscosity curves were drawn and compared with data in chemistry and physics handbook to find the best formula for calculating the viscosity of liquid aluminum in a temperature range from 933 K (melting point) to 1223 K [26], as shown in Fig. 3. Compared with Eq. (2), Eq. (3) and Eq. (4) both conform to the Arrhenius formula, but the variation trend of liquid aluminum viscosity with temperature calculated by Eq. (3) differs greatly from the variation trend of handbook data. The results calculated by Eq. (4) are in good agreement with the handbook data, and the tendency of the viscosity decreasing with increasing temperature is similar to that of the handbook data, so it is more accurate to choose Eq. (4) to calculate the change of the viscosity with temperature. Equation (4) was subsequently compiled as

            (5)

The viscosity of liquid aluminum is divided into three sections according to the temperature interval. When the temperature of liquid aluminum is lower than the melting point (933 K), the aluminum is a solid phase without viscosity. The viscosity of liquid aluminum is set to be infinity to approximate a solid. When the temperature of liquid aluminum is between 933 and 1223 K, the viscosity is calculated according to Eq. (4). In the third section, when the temperature of liquid aluminum is greater than 1223 K, the viscosity changes little and is set to be a fixed value.

2.2 Volume of fluid (VOF) model

The VOF model tracks the interface between aluminum and air by solving a continuity equation for one or more volume fractions of the phase [27]. For the qth phase, the equation has the following form:

            (6)

where t is the time; α_q, ρ_q and u_q are the volume fraction, density and velocity of the qth phase, respectively.

The velocity field is shared between the phases and a single momentum equation that is solved throughout the domain:

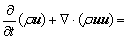
      (7)

where μ and ρ are the mixture viscosity and density, P is the pressure, g is acceleration of gravity, and F represents the forces [28].

The energy equation, also shared among the phases, is shown below:

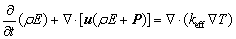       (8)

where T is temperature and k_eff is effective thermal conductivity [29].

2.3 Turbulent model

The flow of liquid aluminum in the troughs is turbulent. A more accurate realizable k-ε model was used to address the turbulent flow. It is an improvement of the standard turbulence model and has better accuracy for the divergence ratio of flat and cylindrical jets. The model used a standard wall function for near-wall treatment.

2.4 Boundary conditions and solution strategies

The setting of boundary conditions is directly related to the correctness of the calculation results. The upper outlet of the mixing furnace was set as pressure outlet boundary conditions, and the outlet pressure was atmospheric pressure. The liquid aluminum outlet of the mixing furnace was set as the internal boundary condition so that the liquid aluminum in the mixing furnace can freely flow out [30]. The other boundaries were set as wall boundary conditions [31]. The initial temperature of liquid aluminum in the mixing furnace was set to be 1023 K.

The calculation was performed on ANSYS FLUENT v. 17.0 and carried out by using the 3D double-precision pressure-based solver. Pressure-velocity coupling was computed by the PISO algorithm. For momentum and energy, the second- order upwind dispersion was selected. The PRESTO dispersion was selected for pressure dispersion, and a first-order upwind dispersion was selected for other parameters. The time step was 0.0001 s. All other settings were kept at the default values.

3 Results and discussion

3.1 Mesh independence verification

To determine the independence of the calculation results for the numbers of meshes, four similar cases with different mesh numbers were investigated. After a typical simulation, the mass flow of liquid aluminum was compared. The verification results are listed in Table 2 when the outlet radius of the mixing furnace is 0.08 m and the height of liquid aluminum is 1.3 m. The relative deviation of the mass flow is 0.95% between No. 2 and No. 3, and the relative deviation of the mass flow is 0.025% between No. 3 and No. 4. Therefore, according to the verification results and excessive computations, No. 3 is retained for the rest of the present work. Its mesh number is 943782.

Table 2 Results of mesh independence verification

3.2 Critical conditions of leakage

The outlet radius of the mixing furnace was increased under different aluminum heights to determine the critical conditions of leakage during the casting process. The outlet radius of the mixing furnace (R) of 0.04, 0.06 and 0.08 m, and the height of liquid aluminum (H) of 1.0, 1.1, 1.2, 1.3, 1.4 and 1.5 m were used. The mass flow of liquid aluminum was monitored at the outlet of the mixing furnace, and two points that monitor the temperature of liquid aluminum were set. The monitoring points were located at the 1/4 and 3/4 of the long trough and they were 1 mm away from the bottom of the trough. The distribution of monitoring points is shown in Fig. 2.

The outflow process of aluminum from the outlet of the mixing furnace is a typical problem of thin-walled small orifice free outflow in fluid mechanics. The characteristic equation of thin- walled small orifice free outflow is [32,33]

                        (9)

where μ′ is the discharge coefficient, g=9.81 m/s², A is the orifice area, and H is the height of the liquid aluminum in the furnace (above the small orifice). μ′ was set to be 0.62 [34]. The comparisons between the simulation data and the theoretical calculation results that are calculated according to Eq. (9) are shown in Fig. 4. The stable mass flow rate at the outlet of the mixing furnace increases with the height of the liquid aluminum and outlet radius. The relative error under different conditions is less than 6%, with a minimum of 0.2%, which verifies the reliability and adaptability of the model to simulate the aluminum casting process.

Fig. 4 Comparison between simulation data and theoretical calculation results

Although the mass flow rate can reach a maximum of 101.7 kg/s according to the simulation results, the liquid aluminum will not leak during the liquid aluminum casting process, as shown in Fig. 5. Under different conditions, the heights of aluminum in the long trough are lower than the critical height of leakage (height of long trough: 0.2 m), indicating that there will not be a leakage during the casting process. The phase distribution cloud diagram is inserted in Fig. 5(a) when the level of the aluminum is the highest in the long trough. It can be concluded that if the outlet radius of the mixing furnace is increased, even if the mixing furnace is filled with liquid aluminum, the liquid aluminum casting process will not leak.

Fig. 5 Aluminum heights in long trough under different conditions (a) and temperature field at 1.4 s (b) and 5 s (c) (R=0.08 m, H=1.3 m)

The temperature field is shown in Figs. 5(b, c). The model was sliced at Z=1.3 m (the centerline of the troughs). The liquid aluminum flows out from the mixing furnace outlet and then flows along the various troughs. The heat transfer process mainly includes four aspects: convection heat transfer between liquid aluminum and air, convection heat transfer between liquid aluminum and troughs, heat conduction inside the troughs and heat radiation from the troughs to air. The molten aluminum flowing in the troughs continuously conducts convective heat transfer with the air, and the heat of the aluminum is gradually transferred to the air nearby, raising its temperature, and then gradually diffuses outwards. At the same time, the trough that first contacts the molten aluminum first radiates heat to the air, and the temperature of the air that contacts the trough wall gradually increases. The longer the heat transfer time, the wider the range of heat transfer.

3.3 Leakage pattern and spread form of liquid aluminum

A simulation study was carried out on the overflow leakage of liquid aluminum due to an outlet blockage of a trough. The outlet of the trough was closed to prevent the liquid aluminum from flowing out of the trough, and the long trough was filled with liquid aluminum in advance. When the liquid aluminum in the mixing furnace flows to the long trough, overflow leakage will occur. The temperature of liquid aluminum that is added into the long trough is obtained by averaging the stable temperature of two monitoring points, as given in Table 3. This is also the temperature at which the liquid aluminum begins to leak.

Table 3 Temperature of liquid aluminum in long trough

The ground roughness was set, and the wall law that contained the roughness function was used to calculate the influence of ground roughness on the spread of leaked aluminum. For rough walls, the wall law of average velocity has the following form:

          (10)

                            (11)

where u_p is the velocity at the grid point near the wall; τ_w is the wall shear stress; 1/k is the slope; E′ is a constant related to the surface roughness; Δy_p is the distance from the near wall node p to the solid wall; C_μ is the empirical constant; △B is a function measuring the wall roughness and is zero for smooth walls. For homogeneous and rough walls, △B is related to dimensionless rough height .

When <2.25, ΔB=0.

When 2.25≤≤90,

             (12)

When >90,

                    (13)

                           (14)

where K_S is the height of the physical roughness and C_S is the roughness constant.

Once the physical roughness height and the roughness constant are known, the value of the roughness function can be calculated, and the influence of ground roughness on the average temperature, wall shear stress and turbulence intensity can be calculated through the wall law that contains the roughness function. The cement ground of the factory is homogeneous and rough. The roughness height was set to be 0.004 m, and the roughness constant was 0.5.

Fig. 6 Leakage patterns of aluminum at different time (R=0.08 m, H=1.3 m)

The model was sliced at Z=1.3 m (the centerline of the troughs), and the liquid aluminum leakage pattern is shown in Fig. 6. Due to the impact of liquid aluminum flowing from the previous trough, the liquid aluminum rapidly increases to form a protrusion and makes liquid aluminum leak on the start of the long trough, as shown in Fig. 6(a). Then, the liquid aluminum in the long trough surges to the end in a wave-like motion. The end of the long trough begins to leak gradually. The leakage time at the start and end of the long trough is different, and this will inevitably results in a unique distribution of leaked aluminum on the ground.

As the leakage gradually increases, the spread distribution of liquid aluminum presents a regular pattern on the ground. The leaked aluminum exhibits a long strip shape distribution on the ground, where the start of the strip is wide and the end of the strip is narrow. This is due to the different leakage times at the start and end of the long trough. The spread form of the leaked aluminum on the ground at different time is shown in Fig. 7.

Fig. 7 Spread form of leaked aluminum on ground at different time (R=0.08 m, H=1.3 m)

3.4 Leakage amount and spread area

The mass flow of the leaked aluminum was monitored, and the mass flow monitoring curve was drawn. The curves were integrated to obtain the leakage of liquid aluminum over a period of time. Figure 8 shows the total leakage amount and spread area when the time is 4.8 s after the start of the leakage.

Fig. 8 Leakage amount (a) and spread area (b) (t=4.8 s)

The leakage amount of liquid aluminum increases with the height of liquid aluminum in the mixing furnace and outlet radius. When the outlet radius is the same, the spread area increases with the height of liquid aluminum; however, the spread area of R=0.06 m is larger than that of R=0.08 m when the height of aluminum in the mixing furnace is lower than 1.2 m. The reason is that the boundary layer sizes of liquid aluminum and air are different. The boundary layer of R=0.06 m is larger than that of R=0.08 m, and the proportion of liquid aluminum to air is small. When calculating the spread area of liquid aluminum, the boundary layer is taken into account. Therefore, the leakage amount of R=0.06 m is less than that of R=0.08 m, but the spread area is greater than that of R=0.08 m when the liquid aluminum in the mixing furnace is lower than 1.2 m.

4 Conclusions

(1) Under different mixing furnace outlet radii (R=0.04, 0.06, 0.08 m), even if the mixing furnace is filled with liquid aluminum (H=1.5 m) and the mass flow is 101.7 kg/s, the liquid aluminum during casting process will not leak.

(2) During the liquid aluminum leakage process, the upstream liquid aluminum initially impinges on the aluminum at the beginning of the long trough, forming a protrusion and causing liquid aluminum leakage. Then, the liquid aluminum in the long trough surges to the end in a wave-like manner, causing continuous liquid aluminum leakage. There is a time difference between the beginning and the end of the long trough, which is also the reason why the leaked aluminum presents a long strip on the ground with a wide beginning and a narrow end.

(3) The leakage amount of liquid aluminum increases with the height and outlet radius; the spread area increases with the height of liquid aluminum. The influence of outlet radius on the spread area is complicated due to the existence of a boundary layer between the liquid aluminum and air.

Acknowledgments

The authors are grateful for the financial supports from the National Key R&D Program of China (2017YFC0805100).

References

[1] KAZAMA M, SUWA T, MAEDA Y. Modeling and computation of casting process by particle method [J]. Journal of Materials Engineering and Performance, 2019, 28: 3941-3949.

[2] BERTHOUD G. Vapor explosions [J]. Annual Review of Fluid Mechanics, 2000, 32: 573-611.

[3] RICHTER R T, EKENES J M. Cause and prevention of explosions involving DC casting of aluminum sheet ingot [C]//GRANDFIELD J F, ESKIN D G. Essential Readings in Light Metals. Cham: Springer, 2016: 1085-1090.

[4] EPSTEIN S. The aluminum industry’s efforts to prevent molten metal explosions [C]//Light Metals. Warrendale: TMS, 2003: 679-682.

[5] EKENES J M, SAETHER T. Cause and prevention of explosions involving hot-top casting of aluminum extrusion ingot [C]//GRANDFIELD J F, ESKIN D G. Essential Readings in Light Metals. Cham: Springer, 2016: 1078-1084.

[6] EKENES M. Training for preventing molten metal explosions in aluminum cast houses [C]//Light Metals. Warrendale: TMS, 2007: 807.

[7] LEON D D, RICHTER R T, LEVENDUSKY T L. Investigation of coatings which prevent molten aluminum/ water explosions [C]//GRANDFIELD J F, ESKIN D G. Essential Readings in Light Metals. Cham: Springer, 2016: 1068-1073.

[8] LIU Yu, LV Zhong-jie, HUANG Feng-lei, GUO Xue-yong, SHEN Zheng-xiang. Experimental study on vapor explosion caused by interaction between high temperature molten aluminum and water [J]. Journal of Beijing Institute of Technology, 2014, 23: 147-151.

[9] LOWERY A W, ROBERTS J. Organic coatings to prevent molten metal explosions [J]. Materials Science Forum, 2009, 630: 201-204.

[10] BABAITSEV I V, KUZNETSOV O V. Energy of explosions occurring when water falls onto a layer of molten metal [J]. Metallurgist, 2001, 45: 185-188.

[11] WOLOSHYN J, GERBER A, PLIKAS T, BAKER D, BLACKMORE A. Overpressure due to a molten aluminum and water explosion in a casthouse [C]//RATVIK A. Light Metals. Cham: Springer, 2017: 1045-1051.

[12] SAHOO S, KUMAR A, DHINDAW B K, GHOSH S. Modeling and experimental validation of rapid cooling and solidification during high-speed twin-roll strip casting of Al-33wt.%Cu [J]. Metallurgical and Materials Transactions B, 2012, 43: 915-924.

[13] WANG Qing, GOSSELIN L, FAFARD M, PENG Jian-pin, Li Bao-kuan. Numerical investigation on the impact of anode change on heat transfer and fluid flow in aluminum smelting cells [J]. Metallurgical and Materials Transactions B, 2016, 47: 1228-1236.

[14] AKBARI S, FRIEDRICH B. Challenges in measuring of physical properties of liquid phases for material and process optimisation [J]. Advanced Engineering Materials, 2007, 9: 280-285.

[15] BROOKS R F, DINSDALE A T, QUESTED P N. The measurement of viscosity of alloys—A review of methods, data and models [J]. Measurement Science and Technology, 2005, 16: 354-362.

[16] CHENG J, GROBNER J, HORT N, KAINER K U, SCHMID-FETZER R. Measurement and calculation of the viscosity of metals—A review of the current status and developing trends [J]. Measurement Science and Technology, 2014, 25: 1-9.

[17] DINSDALE A T, QUESTED P N. The viscosity of aluminium and its alloys—A review of data and models [J]. Journal of Materials Science, 2004, 39: 7221-7228.

[18] ISHIKAWA T, PARADIS P F, OKADA J T, WATANABE Y. Viscosity measurements of molten refractory metals using an electrostatic levitator [J]. Measurement Science and Technology, 2012, 23: 025305.

[19] BAKHTIYAROV S I, OVERFELT R A. Measurement of liquid metal viscosity by rotational technique [J]. Acta Materialia, 1999, 47: 4311-4319.

[20] MORARU L. Viscosity of eutectic silumin alloy in ultrasonic field and estimation of melting temperature [J]. Indian Journal of Pure & Applied Physics, 2007, 45: 733-737.

[21] KAPTAY G. A unified equation for the viscosity of pure liquid metals [J]. Zeitschrift Fur Metallkunde, 2005, 96: 24-31.

[22] GAO Shan-chao, JIAO Ke-xin, ZHANG Jian-liang. Review of viscosity prediction models of liquid pure metals and alloys [J]. Philosophical Magazine, 2019, 99: 853-868.

[23] MALYSHEV V P, MAKASHEVA A M, SULEIMENOV T. Cluster–associate model for the temperature dependence of the viscosity and the density of aluminum [J]. Russian Metallurgy (Metally), 2015, 2015: 443-445.

[24] SUN Min-hua, GENG Hao-ran, BIAN Xiu-fang, LIU Yan. The simulation of the viscosity of liquid aluminum using the tight-binding potential [J]. Materials Science Forum, 2000, 331-337: 337-342.

[25] BATTEZZATI L, GREER A L. The viscosity of liquid metals and alloys [J]. Acta Metallurgica, 1989, 37: 1791-1802.

[26] HAYNES W M. Handbook of chemistry and physics [M]. 95th ed. Boca Raton: CRC Press, 2014.

[27] TANG Bo, XU Yan-xia, SONG Xing-fu, SUN Ze, YU Jian-guo. Effect of inlet configuration on hydrocyclone performance [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 1645-1655.

[28] LI Hai-peng, LI He-jun, QI Le-hua, LUO Jun, ZUO Han-song. Simulation on deposition and solidification processes of 7075 Al alloy droplets in 3D printing technology [J]. Transactions of Nonferrous Metals Society of China, 2014, 24: 1836-1843.

[29] LIU Cheng-cai, HE Jing-shan. Numerical analysis of thermal fluid transport behavior during electron beam welding of 2219 aluminum alloy plate [J]. Transactions of Nonferrous Metals Society of China, 2017, 27: 1319-1326.

[30] EBRAHIMI-MOGHADAM A, FARZANEH-GORD M, ARABKOOHSAR A, MOGHADAM A J. CFD analysis of natural gas emission from damaged pipelines: Correlation development for leakage estimation [J]. Journal of Cleaner Production, 2018, 199: 257-271.

[31] BLASE T A, GUO Z X, SHI Z, LONG K, HOPKINS W G. A 3D conjugate heat transfer model for continuous wire casting [J]. Materials Science & Engineering A (Structural Materials: Properties, Microstructure and Processing), 2004, 365: 318-324.

[32] HE Guo-xi, LYU X D, LIAO Ke-xi, LI Yan-song, SUN Li-ying. A method for fast simulating the liquid seepage- diffusion process coupled with internal flow after leaking from buried pipelines [J]. Journal of Cleaner Production, 2019, 240: 1-19.

[33] HE Guo-xi, LIANG Yong-tu, LI Yan-song, WU Meng-yu, SUN Li-ying, XIE Cheng, LI Feng. A method for simulating the entire leaking process and calculating the liquid leakage volume of a damaged pressurized pipeline [J]. Journal of Hazardous Materials, 2017, 332: 19-32.

[34] YU Ting-chao, ZHANG Xiang-qiu, LIMA NETO I E, ZHANG Tu-qiao, SHAO Yu. Impact of orifice-to-pipe diameter ratio on leakage flow: An experimental study [J]. Water, 2019, 11: 1-10.

浇注过程中铝液泄漏的数值模拟

孔令宇¹，刘小珍¹，石忠宁²，李拓夫¹，王兆文¹，刘爱民¹

1. 东北大学 多金属共生矿生态化冶金教育部重点实验室，沈阳 110819；

2. 东北大学 轧制技术及连轧自动化国家重点实验室，沈阳 110819

摘  要：建立模拟铸造过程中铝液泄漏的模型以预防爆炸，包括瞬态溜槽流动，孔口出流和扩散。将仿真数据和理论计算结果进行比较，验证该模型的适应性和准确性。即使改变混合炉中铝液高度和出口半径，铝液在浇注过程也不会发生泄漏。溜槽中的铝液以波浪状的形式向前移动并引起泄漏，泄漏铝液在地面上的扩散呈长条状，铝液泄漏量和扩散面积随着混合炉中铝液高度的增大而增大。

关键词：铝液泄漏；爆炸；泄漏状态；扩散形态；数值模拟；VOF模型

(Edited by Bing YANG)

Corresponding author: Zhong-ning SHI; Tel: +86-24-83686381; E-mail: znshi@mail.neu.edu.cn

DOI: 10.1016/S1003-6326(21)65496-1

1003-6326/ 2021 The Nonferrous Metals Society of China. Published by Elsevier B.V. & Science Press