文章编号：1004-0609(2007)12-1928-08

圆形挤压件多道次等通道弯角挤压变形机理

徐淑波¹，张国良²，任国成¹，王志刚¹

(1. 山东建筑大学 材料科学与工程学院，济南 250101；

2. 山东省科技情报信息研究所，济南 250100)

摘  要：采用数值模拟和实验研究方法分析圆形纯铝挤压件多道次等通道弯角挤压工艺，发现单道次挤压获得的挤压件的变形分布沿挤压件中心横截面竖直方向变形分布不均匀。通过节点映射法实现各工艺路线的多道次挤压，不同的工艺路线对应的多道次挤压变形分布具有明显差异。多道次挤压后晶粒得到显著细化，变形后晶粒结构较挤压前的退火等轴晶粒大为不同，而且各工艺路线的晶界取向也各不相同，其中旋转90?挤压能够获得大角度晶界分布的等轴晶粒试样，实验结果与有限元分析结果十分吻合。

关键词：等通道弯角挤压；超细晶粒；有限元分析；等轴晶粒；工艺路线

中图分类号：TG 376　　     文献标识码：A

Deformation mechanism of

multi-pass equal channel angular extrusion for round-workpieces

XU Shu-bo¹, ZHANG Guo-liang², REN Guo-cheng¹, WANG Zhi-gang²

(1. School of Materials Science and Engineering, Shandong Jianzhu University, Ji’nan 250101, China;

2. Shandong Institute of Science and Technology Information, Ji’nan 250100, China)

Abstract: Multi-pass equal channel angular extrusion (ECAE) processes for round workpieces were investigated by using numerical simulations and experimental studies. The single-pass ECAE is a non-uniform shear deformation process in the cross-section of the workpiece. The different processing routes for equal round channel angular pressing process were conducted by using node mapping method in multi-pass pressing. The effective strain distributions of different processing routes are obviously different. The grains in the workpiece are refined obviously after multi-pass extrusion. The microstructures of the processed workpieces are different from  the equiaxed grains of the annealing initial workpiece. And the microstructure evolution of the workpiece can be changed via different processing routes. The route with turning angle of 90? can get a distribution of high angle grain boundaries in the workpiece. In addition, the experimental results are in agreement with the finite element analysis results. The microstructure evolutions of grain refinement mechanisms for different multi-pass ECAE processing routes accord with the accumulated effective strain rules in the workpiece.

Key words: equal channel angular extrusion; ultra-fine grains; finite element analysis; equiaxed grains; processing route

材料的内在微观结构对外在宏观特性具有重要影响，材料晶粒平均尺寸越小其屈服强度和硬度越高^[1]。因此，寻求可有效细化晶粒的工艺对于开发力学性能优越的材料具有重要的工业应用前景。Segal等^[2]于20世纪70年代末提出的等通道弯角挤压(Equal Channel Angular Extrusion，ECAE)过程具有工艺简单，生产成本低等显著优点，且该工艺能获得无疏松孔洞的块体超细晶材料，有效避免了残留孔隙对材料产生的不良影响^[3-6]。块体超细晶粒材料具有很多与众不同的特性，可做超高强度材料和超塑性材料等^[7-9]。

ECAE工艺的晶粒细化机理在于通过剧烈塑性变形使挤压件累积到足够应变以达到晶粒细化。目前针对ECAE变形机理的数值模拟多为方形件^[10-12]，Iwahashi等^[10]在实验总结的基础上通过几何关系推导得出ECAE累积等效应变可按下式计算：

虽然方形件在实验过程中可以方便地旋转相应角度准确实现各工艺路线挤压，同时可以简化为平面变形问题^[7]便于求解，但是上述公式计算结果只是变形后的平均值，而且不考虑摩擦，计算结果与实际结果有很大差距。在工业应用中以棒料形式存在的材料较多，因此，获得圆形件挤压过程变形机理同样重要。圆形通道ECAE工艺为三维变形问题，其挤压过程变形机理不同于方形件，同时圆形件在逐次挤压过程中需相应旋转90?的要求涉及空间转换，通过二维有限元分析不能给出多道次挤压件的变形分布及均匀程度。

虽然研究ECAE工艺的有关报道较多^[6-9]，但对圆形通道ECAE工艺的变形机理研究领域大都从金属晶体学的角度进行分析^[13]。实践证明采用实验研究与数值模拟相结合的方法能够更有效地获得挤压过程变形机理，目前国际上采用三维有限元分析圆形通道ECAE变形机理的工作刚刚起步^[14]。因此，本文作者在大量三维有限元模拟分析的基础上，通过宏观变形研究和微观组织观测，分析圆形挤压件晶粒细化的过程，从而获得在挤压过程中晶粒细化、晶界取向优化的具体演化规律，提出了更为接近圆形挤压件的实际变形情况的晶粒组织细化机理。

1  多道次挤压有限元模型与节点映射法

图1所示为圆形件ECAE工艺示意图。为了后续分析的方便，根据变形后挤压过程的几何特征建立XYZ三维坐标系，挤出后的挤压件轴向为X轴，挤出后的挤压件横向为Y轴(垂直于XZ坐标平面)，冲头的下压方向为Z轴。ECAE工艺将挤压件通过2个等圆形横截面相交管道的模具反复挤出而细化晶粒，如图1 所示，2个管道的交角Φ称为模具拐角，拐角处圆弧所对应的圆心角Ψ称为模具圆心角，Ψ从0?到(180?-Φ)之间变化。

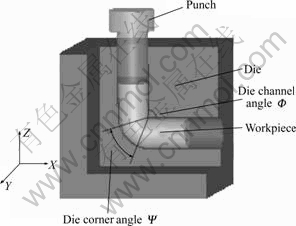
图1  圆形挤压件ECAE工艺示意图

Fig.1  Schematic diagram of ECAE die for round-workpiece

1.1  三维有限元模型

采用塑性成形有限元软件DEFORM^TM对圆形通道ECAE工艺进行了大量数值模拟，图2所示为圆形通道ECAE工艺的有限元模型。假设模具为刚性，挤压件是直径为15 mm，长度为80 mm的圆棒料，网格节点为1 110个，单元数为4 183个。假设材料为刚塑性，在常温下符合应力应变关系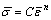，其中，为等效应力，为等效强度，强度系数C=170 MPa，应变指数n=0.24，其它模拟参数如表1所示^[15]。

表1  圆形通道挤压工艺数值模拟参数

Table 1  Parameters for simulation of round-section channel extrusion process

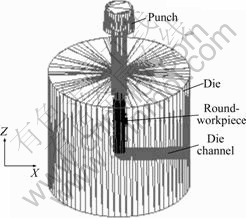
图2  等圆形截面通道弯角挤压模拟有限元模型

Fig.2  Finite element model for simulation of round-section channel ECAE

1.2  节点映射法与多道次挤压工艺路线

多道次挤压件晶粒细化变形均匀程度一直是ECAE工艺研究的热点方向之一，通过改变模具型腔为S型可建立有限元模型^[12]，但模具拐角为90?时，S型工艺获得挤压件相当困难，且该工艺变形机理不同于多道次挤压。采用节点映射法可实现多道次ECAE过程有限元模拟，其关键技术是将前一次挤压获得的与变形历史有关的场变量通过节点映射法传递到下一次挤压^[15]。图3所示为节点映射示意图。图3(a)所示为在前一次挤压终了时挤压件各节点位置，图3(b)所示为下一次挤压初始时挤压件各节点位置。通过节点映射将图3(a)处各节点等效应变准确映射到图3(b)处各节点，如果前一次挤出件网格已重新划分，必须对图3(a)处各节点等效应变进行插值运算，然后再映射到图3(b)处相应各节点。

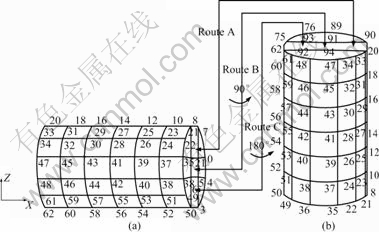
图3  节点映射示意图

Fig.3  Schematic illustration of node mapping method

在多道次挤压过程中，根据挤压件在模具中逐次挤压放置方位的不同，主要有3种挤压工艺路线：路线A，挤压件在逐次挤压过程中一直按同一方位挤压；路线B，挤压件在逐次挤压过程中顺次旋转90?方位挤压；路线C，挤压件在逐次挤压过程中顺次旋转180?方位挤压。多道次挤压过程预实现各工艺路线的数值模拟，对于路线A可直接采用节点映射法实现，由于路线B和C涉及挤压件旋转角度，可在节点映射后，按各工艺路线要求的角度使挤压件模型绕上模轴向方向旋转各路线的对应角度，实现各工艺路线的多道次挤压连续模拟。

1.3  挤压变形分析方法

根据挤压过程的几何特征，图4所示为ECAE挤压过程中从挤压件截取的截面示意图。欲获得挤压件变形过程各场量演化规律，可取模拟初始时挤压件1-1处沿X轴负方向上a~e 5点进行分析；欲获得挤压件主要变形区各场量分布规律，可沿挤出件主要变形区Z轴负方向截取2-2截面进行分析。

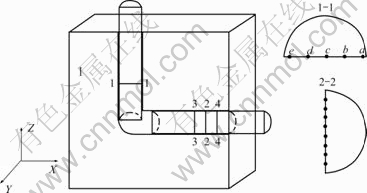
图4  ECAE挤压模拟过程挤压件截取截面示意图

Fig.4  Cross-section setting on workpieces during simulated ECAE process

2  数值模拟

2.1  单道次挤压有限元分析

通过有限元分析了ECAE工艺，该工艺为三维变形，因此必须了解挤压件在各坐标平面的变形分布。图5给出了模具拐角为90?，圆心角半径r=7.5 mm时，挤出件对应XY和XZ和YZ各坐标平面上的等效应变分布。可以看出，变形过程分为3部分：料头部分，最先挤出，变形分布极不均匀，应变分布梯度大；主要变形部分，约占挤压件长度的3/4，沿挤压管道方向应变分布均匀，沿管道截面垂直方向，靠近挤压件上表面部分金属等效应变较大，约为1.08，应变分布呈线性递减至挤压件中央，达到较小值0.815，随后递减趋势减缓达到最小值0.616，最终在靠近下表面金属部分略有回升；料尾部分，即正处于变形部分，变形不完全，如果实现挤压件的连续挤出，则不存在料尾部分，因此可以忽略不计。

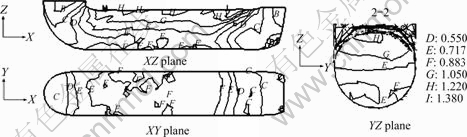
图5  挤压件对应各坐标平面上的等效应变等值线分布

Fig.5  Effective strain distribution in workpiece of different coordinate planes

图6所示为挤压件在挤压入口1-1处截面选取a、b、c、d和e共5点处等效应变随时间的变化曲线。由图可知各曲线等效应变变化分为2个阶段，即ECAE变形部分和ECAE稳定挤出部分。各点通过模具拐角后其等效应变变化较稳定，只呈现缓慢的上升趋势，其中挤压件流经内拐角处金属获得的等效应变梯度较高，而靠近外拐角以及中央部分金属的等效应变分布比较均匀。图7所示为挤压件主要变形区选取的2-2、3-3和4-4处截面进行分析获得的等效应变分布曲线。可知，各截面等效应变分布基本保持不变，虽然挤压件等效应变沿Z轴有一定梯度，但是沿挤出方向基本均匀，因此，在后续分析过程中可选取主要变形区中心2-2横截面进行分析即可获得最终挤出挤压件的变形分布规律。

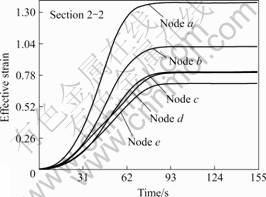
图6  模具拐角为90?、r=7.5 mm时，挤压件挤压过程等效应变演化曲线

Fig.6  Particle tracking result of effective strain in workpieces during ECAE at Φ=90?, r=7.5 mm

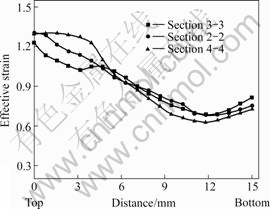
图7  挤压件主要变形区各处的等效应变分布

Fig.7  Effective strain distribution in main deformation zone for processed workpieces

2.2  多道次挤压有限元分析

图8所示为模具拐角90?时，路线A、B和C经4道次挤压后主要变形区2-2处截面的等效应变等值线分布。图8(a)所示为首次挤压获得的等效应变分布，图8(b)~(d)所示为经4道次挤压后，工艺路线A、B和C对应的挤压件横截面上的累积等效应变分布。由图8(a)可知，首次挤压获得的等效应变在竖直方向上不均匀。由图8(b)可知路线A对应挤压件最大等效应变与最小等效应变差值明显，等效应变分布不均匀。由图8(c)可知，挤压件整个横截面变形分布趋向均匀，最大等效应变为3.91，最小等效应变为3.45，通过工艺路线B 4道次挤压后即可获得变形较为均匀的挤压件。由图8(d)可以看出，第4次挤压后路线C对应的挤压件截面等效应变分布较为均匀，最大等效应变为3.95，最小等效应变为3.31。图9所示为A、B和C 3种挤压工艺路线对应2-2处横截面竖直方向上的累积等效应变分布规律。可以看出，各工艺路线通过逐次挤压均可累积足够的等效应变从而达到晶粒细化，但是比较3种工艺路线对应等效应变分布曲线可知，工艺路线A逐次挤压得到的等效应变分布继承了变形不均匀的特点；路线B和C几乎具有相同的累积变形分布，获得的最终挤压件的等效应变分布较均匀，如果考虑挤压件整个横截面的等效应变分布，本文作者认为路线B曲线更为平滑，是最为理想的挤压工艺路线。

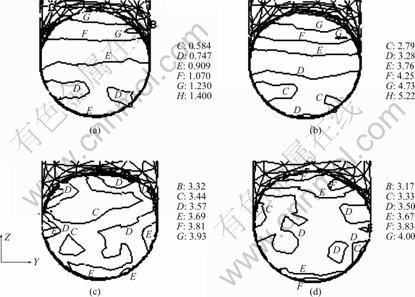
图8  拐角为90?、r=7.5 mm时不同工艺路线对应的等效应变分布

Fig.8  Effective strain contours in cross-section of workpiece for different routes at Φ=90?, r=7.5 mm: (a) One pass; (b) Four passes of route A; (c) Four passes of route B; (d) Four passes of route C

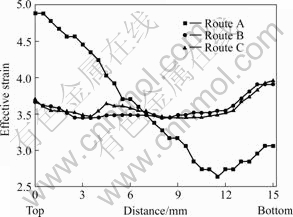
图9  模具拐角90?时路线A、B和C经4次挤压后的等效应变分布规律

Fig.9  Effective strain distribution of routes A, B and C for four passes at Φ=90?

挤压件欲获得均匀的变形分布必须考虑多方面的因素，一方面，选择优化的模具几何形状和工艺参数；另一方面，在多道次挤压过程中选择较好的工艺路线十分重要，但必须保证不同的工艺路线对应相应的挤压次数为一个循环。对于路线A、B和C来讲，连续4次挤压可视为一个挤压循环。因此，在ECAE细化晶粒过程中必须综合平衡或考虑模具几何形状，工艺参数，工艺路线和挤压次数之间的关系，才能获得晶粒几何尺寸均匀的超细晶粒材料。

3  实验研究

为了获得原始挤压件晶粒大小和分布均匀程度的有关信息，首先将试样进行抛光，随后用10% HCLO₄+20%C₃H₈O₃+70% C₂H₅OH溶液电解抛光，然后在10% HFBO₃溶液中阳极覆膜处理4 min，最后通过光学显微镜在偏振光下观察原始试样的微观组织分布。为了探寻晶粒细化演化机理，首先沿挤压件2-2处经线切割减薄取厚度为0.4 mm的圆形薄片试样，再将试样经机械减薄至50 μm，最后采用离子减薄制成薄膜样品，采用透射电镜(H-800，150 kV)进行内部结构分析。

3.1  挤压材料微观组织分布

图10所示为退火后的工业纯铝原始试样显微组织照片。由图可以看出，初始材料的晶粒较首次挤压后的晶粒粗大，晶粒晶界明显呈等轴分布，其晶粒尺寸介于(300±50) μm之间，同时在工业纯铝试样中存在少量其它金属和非金属杂质，由于工业纯铝塑性较好，可保证多道次ECAE实验顺利进行。

图10  工业纯铝原始试样光学显微组织照片

Fig.10  Optical texture in cross section of initial sample for pure aluminium materials

3.2  多道次挤压微观组织演化

具有均匀晶粒尺寸分布的块体超细晶材料在应用中具较高的使用价值，在多道次挤压过程中最终挤出件的晶粒细化分布均匀程度取决于挤出件的等效应变的分布。有限元分析结果表明在多道次挤压过程中通过改变挤压路线可以获得均匀的等效应变分布。但是，晶粒细化与等效应变累积之间的关系还不十分清晰，因此，通过微观组织测试与宏观变形分析相结合的方法研究晶粒细化的演化规律十分必要。

图11所示为首次挤压与3种工艺路线挤压获得的透射电镜及电子衍射斑点照片。中图11(a)所示为纯铝经过首次挤压后的电镜照片，图11(b)~(d)所示为按工艺路线A、B和C挤压4次后同一倍数下晶粒微观组织TEM照片。可以看出，图11(a)首次挤压后晶粒虽得到一定细化，但存在原始的晶粒破碎组织和晶界，同时组织不均匀。挤压4次后各工艺路线均能获得细化后的晶粒组织，但不同的工艺路线对应晶粒分布以及晶界取向角度差别十分明显。图11(b)中路线A挤压件试样晶粒得到明显细化，在视场中出现的大部分晶粒为低角度晶界的拉长形晶粒，具有明显的剪切变形特征。图11(c)中经路线B细化后的晶粒多为等轴晶粒，晶粒分布较为均匀。图11(d)中路线C挤压件试样晶粒同样得到显著细化，在视场中出现较多的等轴晶粒，同时也存在少量细长晶粒。比较图11中各路线对应衍射斑点，可以看出，出现环状斑点表明晶粒得到细化，对应图11(b)中路线A几乎很难发现具有高角度的衍射斑点，从图11(c)中路线B试样晶界衍射斑点可知存在较多高角度晶粒边界，而图11(d)在发现高角度晶界的同时也发现有小角度晶界。因此可以认为路线B的晶粒细化效果最好，路线A最差，根据有限元分析结果可知其原因在于路线A继承了单道次挤压变形不均匀的特点。同时，各工艺路线微观组织的共同特点是获得的超细晶粒材料的缺陷均以位错形式存在，但不同工艺路线位错的存在方式和密度不同，其晶粒细化过程可以认为是一个位错的产生、增殖、湮灭及回复的动平衡过程。

图11  首次挤压与3种工艺路线挤压获得的透射电镜及电子衍射斑点照片

Fig.11  TEM images and SAED patterns for pure aluminum after ECAE process: (a) TEM micrographs through first pass; (b) TEM image through four passes for route A; (c) TEM image through four passes for route B; (d) TEM image through four passes for route C

4  结论

1) 单道次挤压件主要变形部分沿管道挤压方向的应变分布均匀，但沿其横截面从上到下挤压件应变梯度较高，变形分布不均匀。多道次挤压，工艺路线A逐次挤压得到的等效应变分布继承了变形不均匀的特点；工艺路线B和C获得的最终挤压件的等效应变分布比较均匀，其中路线B获得的挤压件的等效应变分布更为均匀。

2) 采用工艺路线B，挤压件能获得较为均匀的等效应变分布。在多道次挤压过程中应选择较好的工艺路线，但必须保证不同的工艺路线获得的最终挤压件对应相应的挤压次数为一个循环。对于路线A、B和C，连续4次挤压可视为一个挤压循环。

3) 初始退火试样为传统的等轴粗大晶粒组织，微观组织分析表明首次挤压后晶粒虽得到显著细化，但挤压件横截面微观组织主要呈现低角度的晶界，细长型的晶粒表明变形具有明显的剪切变形特征。挤压4道次后最终其晶粒尺寸为300~700 nm，路线A试样大部分晶粒为低角度晶界的拉长形晶粒；路线B试样大部分晶粒晶界角度取向多为高角度的等轴晶粒；路线C获得的试样同样出现较多的等轴晶粒，但同时也存在少量细长晶粒，细化后的晶粒晶界明显。

4) ECAE挤压过程中晶粒细化的演化规律基本与等效应变累积规律具有一致性。各工艺路线的微观组织的共同特点是获得的超细晶粒材料的缺陷均以位错形式存在，但不同工艺路线位错的存在方式和密度不同，可以认为晶粒细化过程在宏观变形上是寻求优化的工艺参数、合适的挤压次数和较好工艺路线的过程，从微观组织上是控制位错产生、增殖和湮灭的动平衡的过程。

REFERENCES

[1] Hall E O. Deformation and ageing of mild steel(Ⅲ): Discussion of results[J]. Proceedings of the Royal Society of London Series B: Biological Sciences, 1951, 64(2): 747-753.

[2] Segal V M, Reznikov V I, Drobyshevskiy A E, Kopylov V. Plastic working of metals by simple shear[J]. Russian Metallurgy, 1981, 19(1): 99-105.

[3] Valiev R Z, Islamgaliev R K, Alexandrov I V. Bulk nanostructured materials from severe plastic deformation[J]. Progress in Materials Science, 2000, 45(2): 103-189.

[4] 张 郑, 王经涛, 赵西城. 7475铝合金ECAP的晶粒细化极限[J]. 中国有色金属学报, 2004, 14(9): 741-745.
ZHANG Zheng WANG Jing-tao, ZHAO Xi-cheng. Microstructure and grain refinement limit of 7475 aluminum alloy after equal-channel angular pressing[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(9): 741-745.

[5] Segal V M. Severe plastic deformation: Simple shear versus pure shear[J]. Mater Sci Eng A, 2002, 338(1/2): 331-344.

[6] 刘 咏, 唐志宏, 周科朝, 李志友. 纯铝等径角挤技术(Ⅰ)—显微组织演化[J]. 中国有色金属学报, 2003, 13(1): 21-26.
LIU Yong, TANG Zhi-hong, ZHOU Ke-chao, LI Zhi-you. Equal channel angular pressing process(ECAP) of pure Al(Ⅰ)—Microstructure evolution[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(1): 21-26.

[7] Furukawa M, Horita Z, Nemoto M. The use of severe plastic deformation for microstructural control[J]. Mater Sci Eng A, 2002, 324(1): 82-89.

[8] Horita Z, Matsubara K, Makii K, Terence G. A two-step processing route for achieving a superplastic forming capability in dilute magnesium alloys[J]. Scripta Materialia, 2002, 47(4): 255-260.

[9] 唐志宏, 黄伯云, 周科朝, 刘 咏. 超细晶材料制备新工艺—等径角挤压[J]. 材料导报, 2001, 15(8): 16-19.
TNAG Zhi-hong, HUANG Bai-yun, ZHOU Ke-chao, LIU Yong. New technology of producing ultra-fine grained microstructure through equal channel angular pressing[J]. Materials Review, 2001, 15(8): 16-19.

[10] Iwahashi Y, Wang J, Horita Z, LIU Yong. Principle of equal channel angular pressing for the processing of ultra-fine grained materials[J]. Scripta Materialia, 1996, 35(2): 143-146.

[11] Semiatini S L, Delo D P, Shell E B. The effective of material properties and tooling design on deformation and fracture during equal channel angular extrusion[J]. Acta Materialia, 2000, 48(8): 1841-1851.

[12] Rosochowski A, Olejnik L. Numerical and physical modelling of plastic deformation in 2-turn equal channel angular extrusion[J]. Journal of Materials Processing Technology, 2002, 154(125/126): 309-316.

[13] 刘 咏, 唐志宏, 周科朝, 李志友. 纯铝等径角挤技术(Ⅱ)—变形行为模拟[J]. 中国有色金属学报, 2003, 13(2): 294-299.
LIU Yong, TANG Zhi-hong, ZHOU Ke-chao, LI Zhi-you. Equal channel angular pressing process of pure aluminum(Ⅱ)—Simulation of deformation behavior[J]. The Chinese Journal of Nonferrous Metals, 2003, 13(2): 294-299.

[14] Xu S, Zhao G, Luan Y, Guan Y. Numerical studies on processing routes and deformation mechanism of multi-pass equal channel angular pressing processes[J]. Journal of Materials Processing Technology, 2006, 176(1/3): 251-259.

[15] Altan T, Oh S, Kobayashi S, Horita Z. Metal forming: Fundamentals and applications[M]. Ohio: American Society for Metals, 1983: 55-71.

基金项目：国家自然科学基金资助项目(50425527)；山东省优秀中青年科学家科研奖励基金资助项目(2007BS05004)

收稿日期：2007-04-17；修订日期：2007-08-22

通讯作者：徐淑波，博士；电话：0531-86367285；E-mail: xsb@sdjzu.edu.cn

(编辑 李向群)