基于分阶段Wiener-Einstein过程设备的实时可靠性评估
王小林,郭波,程志君
(国防科技大学 信息系统与管理学院,湖南 长沙,410073)
摘要:对分阶段退化情况下设备实时可靠性评估的方法进行研究。针对分阶段非单调的退化过程,提出分阶段Wiener-Einstein退化过程模型;然后,推导该模型下的可靠度函数,并给出对设备可靠度进行实时评估的方法;最后,基于该模型对液力耦合器的可靠性进行评估。研究结果表明:该退化模型能够很好描述液力耦合器分阶段的退化过程,且能够给出可信的可靠性评估结果。
关键词:分阶段Wiener-Einstein过程;实时可靠性评估;液力耦合器
中图分类号:TB114.3 文献标志码:A 文章编号:1672-7207(2012)02-0534-07
Real-time reliability evaluation of equipment based on separated-phase Wiener-Einstein process
WANG Xiao-lin, GUO Bo, CHENG Zhi-jun
(College of Information System and Management, National University of Defense Technology, Changsha 410073, China)
Abstract: A method about real-time reliability evaluation for the equipment whose degradation process was separated into different phases was studied. Firstly, separated-phase Wiener-Einstein process was proposed to model equipment’s degradation process which was obviously separated into different phases. Then the reliability function based on this degradation model and the updating method were presented. Finally, the method was applied to evaluate the real-time reliability of liquid coupling device (LCD). The results show that the presented degradation model can depict LCD’s separated-phase degradation process effectively, and the believable reliability evaluation is gained by the proposed method.
Key words: separated-phase Wiener-Einstein process; real-time reliability evaluation; liquid coupling device (LCD)
与传统寿命数据统计方法相比,性能可靠性技术能够用于建立性能与可靠性之间的有机联系,具有明显的优越性,是现代可靠性工程中一个新的研究方向。基于性能数据对设备的可靠性进行评估,一个关键步骤就是对设备性能退化数据建模,建模质量直接决定着结果的可信度。目前,对性能退化数据的建模主要有3种方法:基于性能退化轨迹、基于性能退化量的分布以及基于随机过程。对于性能退化特征明显、退化机理容易理解的产品来说,可以利用退化轨迹对设备的退化过程进行建模,从而能够对设备未来的退化量进行预测并评估设备的可靠度。如Lu等[1-2]介绍了几种线性退化轨迹,并给出相应的统计方法;Gebraeel等[3-4]利用指数模型建立轴承的退化轨迹,并对轴承的剩余寿命进行了预测。当设备的退化机理不明显,且相同测量时刻存在大量数据时,可以利用退化量的分布对性能退化数据进行建模[5-6]。此外,Zuo等[7]对这方面的成果进行了总结,并基于此方法对金属表面焊接点的热疲劳情况进行了研究。然而,这种方法也存在着缺点,如大样本,这个条件有时很难满足;另外,该建模方法在一定程度上忽视了退化数据的方向性。
与前2种方法相比,基于随机过程的建模能够更好地反映环境等因素对设备性能的影响,能够反映设备的真实退化过程,因此,很多研究者对此进行了研究。其中,有2类随机过程常被用于退化过程的建模,即Gamma过程和Wiener过程。Gamma过程适用于描述设备性能单调退化的情形,为此,在可靠性评估以及维修决策中经常被用来对设备的退化过程进行建 模[8-9]。与Gamma过程相比,Wiener过程则适用于非单调退化情况下的建模。如Whitmore[10]利用Wiener过程对晶体管的退化数据进行建模,拟合效果较好;Wang[11]在假定退化过程为Wiener过程的情况下,给出了参数与非参数相结合的估计方法以及收敛性的证明,并将该模型应用于桥横梁退化过程建模。Wiener过程在加速退化过程中的应用见文献[12]。设备在实际工作环境中往往受到多种应力的综合作用,利用随机过程描述设备退化更符合工程实际。然而,在已有的基于随机过程建模的文献中,大都假设设备的退化过程为单一的随机过程,有时这样的假设是不合实际的,如液力耦合器开始退化较快,到达一定的性能值后退化得较缓慢;另外,有的设备可能开始退化平缓,最后退化很快,这样明显的分阶段退化很难用单一的随机过程进行描述。为此,针对分阶段非单调的退化过程,本文作者首先提出分阶段Wiener-Einstein过程模型;然后,根据该退化模型推导对应的可靠度函数;进一步考虑Wiener-Einstein过程中漂移系数与扩散系数的随机性,并利用Bayes方法对设备可靠度函数进行实时更新;最后,利用该模型对液力耦合器可靠性进行评估,证明该模型的有效性。
1 分阶段Wiener-Einstein退化过程模型
分阶段的退化过程在现实中是存在的,图1描述的是3台液力耦合器的退化轨迹。从图1可以看出:液力耦合器的振幅随着时间的增加有增大的趋势,并且存在着一定范围内非单调的退化特征,如LCD 3的退化轨迹。另外,从总体上看,LCD的退化明显分为2个阶段:以振幅近30 mm为界,前面一个阶段退化较快,而后退化较为平缓。这样的退化过程无法用单一的随机过程进行描述,否则将不能反映液力耦合器的真实退化过程。为此,本文针对这样分阶段的非单调退化过程,提出分阶段Wiener-Einstein退化过程 模型。
1.1 退化模型的假定
这里通过下述假定来研究分阶段退化过程的建模。
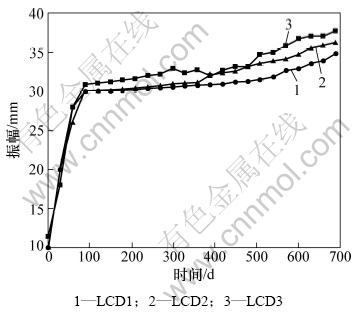
图1 液力耦合器的退化过程
Fig.1 Degradation trajectory of LCD
假定1 X(t)表示设备在t时刻的性能值(如振幅等),若X(t)>ζ(其中ζ为失效阈值),则设备失效;
假定2 设备的性能呈现明显的两阶段的退化,且这2个阶段以设备性能值首次到达D的时刻分界,即当t≤t
D时,设备性能按X
1(t)退化,反之按X
2(t′)进行退化。 其中:X
1(t)表示第1阶段的退化量随时间的增量;X
2(t′)表示第2阶段的退化量随时间的增量;(t′=t-t
D);
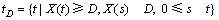
它表示设备性能值首次到达D的时刻。
假定3 每个阶段的退化规律用Wiener-Einstein过程进行描述,即
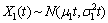 ,
,
假定4 设备的性能可以进行多次测量。
1.2 退化模型的建立
基于上述假设,可以建立两阶段退化过程模型;

 (1)
(1)
式中: 为示性函数;X(0)为初始性能值;X(tD)为阶段分界值。当X1(t)和X2(t′)都为Wiener- Einstein过程时,式(1)就称为两阶段Wiener-Einstein退化过程模型。
为示性函数;X(0)为初始性能值;X(tD)为阶段分界值。当X1(t)和X2(t′)都为Wiener- Einstein过程时,式(1)就称为两阶段Wiener-Einstein退化过程模型。
仿照式(1),可以写出多阶段退化过程模型,即
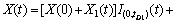
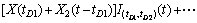
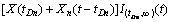 (2)
(2)
式中:X(tD1),…,X(tDn)表示阶段分界值,此模型还可以进行拓展,如X1(t),X2(t′),…,Xn(t′)分别为不同的随机过程模型。
2 可靠度的确定与更新
基于式(1)中的退化模型,下面给出该模型所对应的可靠度函数,并利用Bayes方法对可靠度进行实时更新,以提高评定的精度。
2.1 可靠度函数的确定
若设备的性能值随时间的增加有变大的趋势,设备的可靠度为:
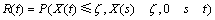 (3)
(3)
根据式(1)和(3),分阶段退化过程模型所对应的可靠度函数可表示为
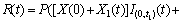
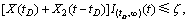 X(τ)<ζ,0≤τ<t) (4)
X(τ)<ζ,0≤τ<t) (4)
对于一直工作的设备,式(3)和(4)不能反映它的实时可靠度。为此,可以按照文献[13]中的定义,假设设备在tm时刻正常的条件下,则其t=tm+Δt时刻的实时可靠度为
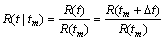 (5)
(5)
若设备当前的性能值为X(tm), 则
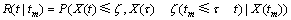 (6)
(6)
在参数已知的条件下,根据式(6),设备的实时可靠度为
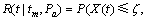
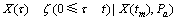
(7)
式中: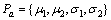 表示模型中的参数。与单一的Wiener-Einstein过程不同,因X(t)为两阶段的Wiener-Einstein过程,R(t|tm,Pa)的表达式需要分情况进行分析。本文分2种情况进行讨论,即tm≤tD≤∞与tm>tD。
表示模型中的参数。与单一的Wiener-Einstein过程不同,因X(t)为两阶段的Wiener-Einstein过程,R(t|tm,Pa)的表达式需要分情况进行分析。本文分2种情况进行讨论,即tm≤tD≤∞与tm>tD。
(1) 当tm≤tD≤∞时,对于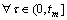 ,有X(τ)≤D。设f(tD|X(tm),Pa)表示tD的条件概率密度函数,则R(t|tm,Pa)可由下式给出:
,有X(τ)≤D。设f(tD|X(tm),Pa)表示tD的条件概率密度函数,则R(t|tm,Pa)可由下式给出:
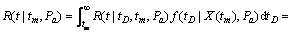

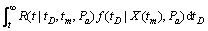 (8)
(8)
设

,可以看成退化刚进入第2阶段后的剩余寿命,则

(9)


式中:P(T>t-tD|Pa)可以根据Wiener-Einstein过程的首达时分布确定[14-15],即

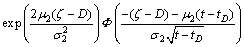 (10)
(10)
同理,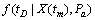 可表示为:
可表示为:

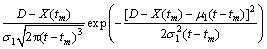 (11)
(11)
综合上述分析,可得在tm≤tD<∞的条件下,R(t|tm,Pa)为:


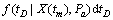 (12)
(12)
另外,若D不是确定的值,而是一个范围A,假设其分布密度函数为fD(x),则上式可扩展为
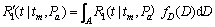 (13)
(13)
(2) 当tm>tD时,即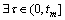 使得X(τ)>D成立,此时设备的退化已处于第2个阶段,可靠度可由下式给出:
使得X(τ)>D成立,此时设备的退化已处于第2个阶段,可靠度可由下式给出:

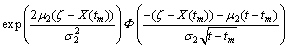 (14)
(14)
2.2 可靠度函数中参数的实时更新
由于设备个体的差异以及环境应力的综合作用,将带来Wiener-Einstein过程中漂移系数与扩散系数的不确定性。为了提高评定的精度,需要不断对这2个参数进行更新。
假设设备的退化过程为Wiener-Einstein过程,即Y(t)=μt+σW(t)。本文选用文献[11,14]中所介绍的Gamma-Normal分布作为(w,μ)的先验分布(式中,w=1/σ2)。记Gamma-Normal分布的密度函数为 f(w,μ)=GN(a,b,d,c),其表达式为:
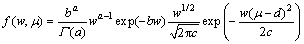 (15)
(15)
因文献[11,14]不是假设设备的退化过程为Wiener-Einstein过程,为此下面对该假设下的参数后验分布进行简要推导。
假设设备的退化数据为Data={y(t1),y(t2),…,y(tn)},则(w,μ)后验分布可根据贝叶斯方法给出,即
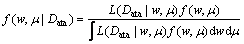 (16)
(16)
通过计算,式(16)可化简为:

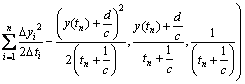 (17)
(17)
其中: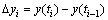 ;
;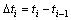 。由此可以看出Gamma-Normal分布为该过程下的共轭先验分布。
。由此可以看出Gamma-Normal分布为该过程下的共轭先验分布。
针对两阶段Wiener-Einstein退化失效过程,可以假设2个阶段参数的先验分布为:
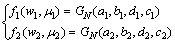
获得分阶段的退化数据Data后,按照上述方法对这2个先验分布进行更新。其步骤为:若只获得第1阶段的退化数据,则只对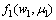 进行更新,即
进行更新,即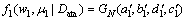 ,
,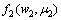 保持不变;相反,则
保持不变;相反,则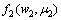 更新为
更新为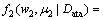
 。
。
2.3 可靠度的实时更新
得到参数的后验分布后,可以对可靠度进行实时更新。在tm≤tD<∞条件下,式(12)可更新为:

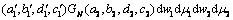 (18)
(18)
同理,在tm>tD时,则式(14)可更新为:
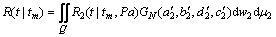 (19)
(19)
式(18)和(19)属于多维条件下的贝叶斯积分问题,其计算可以借助MCMC(Markov Chain Monte Carlo)方法[16]。当已知参数先验分布中的超参数值时,就可以直接按照上述思路对设备的可靠度进行实时更新;若超参数值未知,则需要对其进行估计。为此,下面给出超参数估计的方法。
3 超参数的估计
从上面的分析可知:要对设备的可靠度进行实时评估,需要确定2个先验分布中的超参数。这里按照第二类极大似然方法的思想,采用EM算法[11]给出这些超参数的估计方法。
假设有M个设备,每个设备的退化过程为维纳过
程,即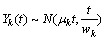 (其中,k=1,…,M),且
(其中,k=1,…,M),且
 。现同时对M个设备进行退化实验(无一失效),获得的退化数据为:
。现同时对M个设备进行退化实验(无一失效),获得的退化数据为:
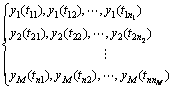
令 ,
,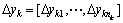 (其中,
(其中, ),引入2组潜在数据,即
),引入2组潜在数据,即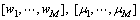 ,则完全似然函数可以写为:
,则完全似然函数可以写为:


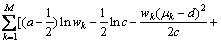
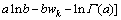 (20)
(20)
根据EM方法,通过E步可求得对数似然函数关于潜在变量的期望值。令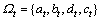 表示迭代t步后所得的超参数的估计值,通过分析可以看出式(20)中关于潜在变量的期望涉及
表示迭代t步后所得的超参数的估计值,通过分析可以看出式(20)中关于潜在变量的期望涉及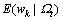 ,
,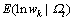 ,
,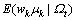 以及
以及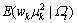 的计算,下面直接给出它们的结果:
的计算,下面直接给出它们的结果:

 (21)
(21)

 (22)
(22)
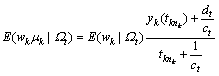 (23)
(23)
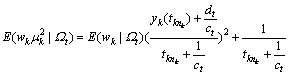 (24)
(24)
将上述结果替代式(20)中的潜在变量的表达式,即可完成E步。进一步根据M步可得第t+1步的超参数迭代值(Ωt+1),即

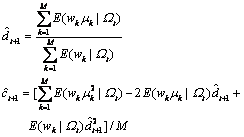 (25)
(25)
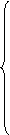
 (26)
(26)
式中: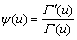 ,可以用
,可以用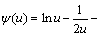
 进行近似。这样重复E步和M步,直
进行近似。这样重复E步和M步,直
到满足一定的收敛精度时(如前、后2次似然函数之差小于某一给定值),便可最终得到相应超参数的估计值。
同理,针对两阶段Wiener-Einstein退化过程,获得M个设备的退化数据后,先把每个设备的退化数据按阶段分成2类;然后,按照上述方法对每个阶段的数据进行处理,可确定2个阶段的先验分布:

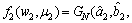
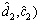
4 实例
下面以液力耦合器(LCD)为研究对象,对文中提出的模型进行应用研究。液力耦合器是高速给水泵的驱动装置,它是以油压来传递动力的无极变速装置。根据发电设备状态评估技术及专家意见,随着使用时间的增长,液力耦合器的振动幅值会不断增大;当振动幅值超过额定阈值即ζ=40 mm时,液力耦合器系统将发生退化失效。因此,选择振幅作为液力耦合器的状态参数。另外,为了方便应用,根据图1所传递的直观信息,假设D=30 mm,即以振幅值30 mm为界,将液力耦合器的退化分成2个阶段。
根据图1,先按照EM算法对超参数进行估计,估计结果如表1所示。从表1可以看出:2个阶段的差异明显。其中比较直观的是d,它表示振幅的平均退化率,其在第1阶段为0.220 3,第2阶段为 0.009 2。2个阶段的退化速率差别较大,无法用单一的随机过程对液力耦合器的整个退化过程进行描述,同时也说明本文的模型可以描述这种差异。
获得参数的估计值后,基于这些估计值,本文通过仿真的方法来验证模型的有效性。基于以上数据求
表1 先验分布中参数的估计值
Table 1 Parameters’ evaluation for prior distribution

出w1,μ1,w2和μ2的估计值(求后验均值),然后通过仿真的方法求得每台液力耦合器的退化轨迹,如图2所示。
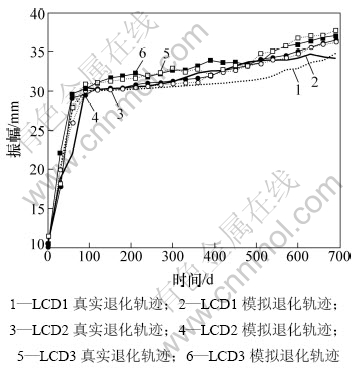
图2 仿真数据与实际数据的比较
Fig.2 Comparison between real data and simulated data
图2所示为10次仿真的平均结果与原始数据的对比。从图2可以看出:所建的模型能够较好地反映液力耦合器分阶段的退化过程(由于随机性的影响,这样的误差是可以接受的)。本文作者通过多次仿真,得到了相同的结论,这证明本文所建的模型是有效的。
通过以上分析,说明本文所建的模型能够有效地反映液力耦合器的退化过程。下面将基于该模型对其可靠性进行评估。首先给出LCD1退化到60 d时的实时可靠度曲线,如图3所示。
从图3可以看出:2条曲线的差异较大。从后面的观测可以看出:图3(a)给出的结果与实际相差较大,进一步说明液力耦合器的退化过程难以用单一的随机过程进行描述。
下面以LCD1为例,研究不同时刻可靠性评估的差异,结果如图4所示。
图4所描述的是LCD1分别退化到60 d和690 d时所给出实时可靠度曲线。从图4可以看出:对于长区间上的可靠性评估,曲线1给出了较为保守的估计结果(从图1可以看出:LCD1在690 d时的振幅为34.802 0,与失效阈值相差5.198 0)。这也反映出实时监测的重要性。只有不断地监测设备的性能才能够准确把握设备的状态,从而实现设备可靠性的实时评估。
为了对不同设备的可靠性进行比较,下面给出LCD1,LCD2和LCD3退化到690 d时的实时可靠度曲线,如图5所示。
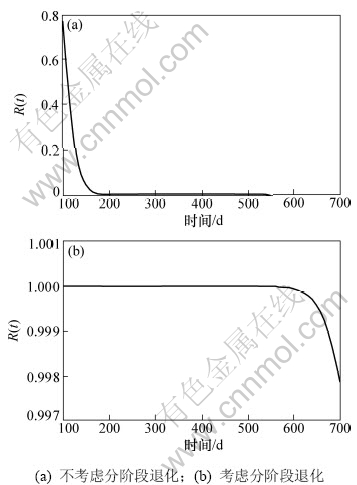
图3 LCD1退化到60 d时的实时可靠度曲线
Fig.3 Real-time reliability curves of LCD1 survived to 60 d
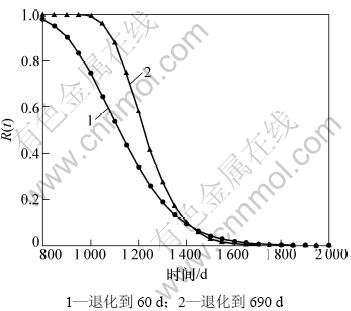
图4 LCD1退化到60 d和690 d时的实时可靠度曲线
Fig.4 Real-time reliability curves of LCD1 survived to 60 d and 690 d
从图5可以看出:LCD1,LCD2和LCD3的可靠度呈现递减的趋势,这与3台设备当前的状态差异相吻合(从图1可以看出,它们当前的性能值分别为34.802,36.216和37.703,与失效阈值分别相差 5.198 0,3.784 0和 2.297 0),因此,本文的评估方法也能够反映不同设备之间的差异。
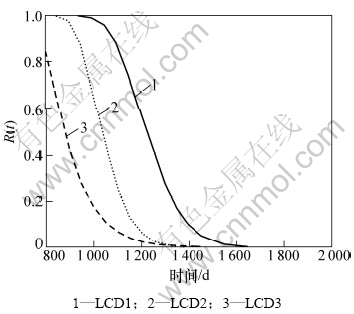
图5 LCD1,LCD2和LCD3退化到690 d时的实时可靠度曲线
Fig.5 Real-time reliability curves of LCD1,LCD2 and LCD3 survived to 690 d
5 结论
(1) 建立了分阶段Wiener-Einstein退化过程模型,推导了该退化模型下的可靠度函数。
(2) 利用EM算法给出了先验分布中超参数的迭代估计表达式,从而确定参数的先验分布,为利用贝叶斯方法实现可靠度的实时更新奠定了基础。
(3) 本文提出的模型能够很好地拟合分阶段的退化过程,且能够有效地评估符合该退化过程设备的实时可靠性。此外,本文的建模方法可以推广到多阶段的退化建模,还可以用不同的退化模型来描述阶段之间的差异。
参考文献:
[1] Lu J C, Park J, QING Yang. Statistical inference of a time-to-failure distribution derived from linear degradation data[J]. Technometrics, 1997, 39(4): 391-400.
[2] Meeker M Q, Escobar L A. Statistical methods for reliability data[M]. New York: John Wiley & Sons, 1998: 128-137.
[3] Gebraeel N Z, Lawley M A, Li R, et al. Residual-life distributions from component degradation signals: A Bayesian approach[J]. IIE Transactions, 2005, 37(6): 543-557.
[4] Lawley M A, Gebraeel N Z. Real-time estimation of mean remaining life using sensor-based degradation models[J]. Journal of Manufacturing Science and Engineering, 2009, 131(5): 59-59.
[5] HUANG Wei. Reliability analysis considering product performance degradation[D]. Arizona: The University of Arizona, 2002: 32-61.
[6] YANG Kai, XUE Jian-an. Continuous state reliability analysis[C]//Annual Reliability & Maintainability Symposium. Las Vegas: Elsevier, 1996: 251-257.
[7] ZUO Ming-jian, JIANG Ren-yan, Yam R. Approaches for reliability modeling of continuous-state devices[J]. IEEE Transactions on Reliability, 1999, 48(1): 9-18.
[8] Noortwijk J M, Frangopol D M. Two probabilistic life-cycle maintenance models for deteriorating civil infrastructures[J]. Probabilistic Engineering Mechanics, 2004, 19(4): 345-359.
[9] Noortwijk J M, Weide J M, Kallen M J, et al. Gamma processes and peaks-over-threshold distributions for time-dependent reliability[J]. Reliability Engineering and System Safety, 2007, 92(12): 1651-1658.
[10] Whitmore G A. Estimating degradation by a wiener diffusion process subject to measurement error[J]. Lifetime Data Analysis, 1995, 1(3): 307-319.
[11] Wang X. Wiener processes with random effects for degradation data[J]. Journal of Multivariate Analysis, 2010, 101(2): 340-351.
[12] Whitmore G A, Schenkelberg F. Modeling accelerated degradation data using Wiener diffusion with a time scale transformation[J]. Lifetime Data Analysis, 1997, 3(1): 27-43.
[13] Lu H, Kolarik W J, Lu S S. Real-time performance reliability prediction[J]. IEEE Transactions on Reliability, 2001, 50(4): 353-357.
[14] Whitmore G A. Normal-gamma mixtures of inverse Gaussian distributions[J]. Scandinavian Journal of Statistics, 1986, 1(3): 211-220.
[15] 赵建印, 刘芳, 孙权, 等. 金属化膜脉冲电容器在线可靠性评估与性能预计[J]. 兵工学报, 2006, 27(3): 265-268.
ZHAO Jian-yin, LIU Fang, SUN Quan, et al. On-line reliability estimation and performance prediction for metallized film pulse capacitor[J]. Acta Armamentarii, 2006, 27(3): 265-268.
[16] Robinson M E, Crowder M J. Bayesian methods for a growth-curve degradation model with repeated measures[J]. Lifetime Data Analysis, 2000, 6(4): 357-374.
(编辑 陈灿华)
收稿日期:2011-02-18;修回日期:2011-04-25
基金项目:国家青年自然科学基金资助项目(60904002)
通信作者:王小林(1985-),男,云南曲靖人,博士研究生,从事装备综合保障与可靠性分析研究;电话:0731-84573550;E-mail:yibanwang350424@163.com