DOI： 10.11817/j.issn.1672-7207.2021.02.014
基于实时电路模型的储能系统锂离子电池状态估算
陈霖华1, 2，陈剑2，徐志强1, 2，夏向阳3，曾小勇3，石超3，周文钊3
(1. 湖南经研电力设计有限公司，湖南 长沙，410004；
2. 国网湖南省电力公司经济技术研究院，湖南 长沙，410004；
3. 长沙理工大学 电气与信息工程学院，湖南 长沙，410004)
摘要：为了充分发挥锂离子电池在电力系统储能中的潜力，需要准确了解电池组的荷电状态(state of charge，SOC)和健康状态(state of health，SOH)，为此，提出一种新的SOC和SOH估算方法。该方法基于锂离子电池二阶电路模型，将锂离子电池实际运行过程中的输出电压测量值和所建立的仿真模型端口电压进行比较，利用PI控制器对所建立的电池模型欧姆内阻和开路电压进行修正，得到更精确的SOC和SOH估计值；最后，进行开展电池的充放电试验。研究结果表明：相比扩展卡尔曼滤波法(Extended Kalman Filter，EKF)和库仑计数法(Coulomb Counting，CC)，所提出的方法对SOC和SOH估算精度更高，验证了所提出的策略的有效性。
关键词：锂离子电池；荷电状态(SOC)；健康状态(SOH)；PI控制器
中图分类号：TM912.1 文献标志码：A OSID：
文章编号：1672-7207（2021）02-0458-07
State estimation of lithium ion battery in energy storage system based on real time circuit model
CHEN Linhua1, 2, CHEN Jian2, XU Zhiqiang1, 2, XIA Xiangyang3, ZENG Xiaoyong3,
SHI Chao3, ZHOU Wenzhao3
(1. Hunan Economic Research Power Design Institute, Changsha 410004, China;
2. State Grid Research Institute of Hunan Province Economics and Technology, Changsha 410004, China;
3. School of Electrical and Information Engineering, Changsha University of Science & Technology, Changsha 410004, China)
Abstract: In order to give full play to the potential of lithium-ion batteries in power system energy storage, it is necessary to accurately understand the state of charge(SOC) and state of health(SOH) of batteries, therefore, a new SOC and SOH estimation method was proposed. Based on the second-order circuit model of lithium-ion battery, this method compared the measured output voltage of lithium-ion battery in the actual operation process with the port voltage value of the simulation model. According to the difference between the two values, PI controller was used to modify the ohmic internal resistance and no-load voltage of the battery model to obtain more accurate SOC and SOH estimation values. Finally, the battery charge and discharge test were made. The results show that the SOC and SOH estimation accuracies of the proposed strategy are higher than those of the extended Kalman filter (EKF) and Coulomb counting method(CC), which verifies the effectiveness of the proposed strategy.
Key words: lithium battery; state of charge(SOC); state of health(SOH); PI controller
锂离子电池具有高工作电压、高能量比、低自放电率和较高的循环寿命等优势，已成为新能源汽车、电网等中储能系统的主流选择[1-3]。在诸多储能技术路线中，电化学储能装置响应时间为毫秒级，相对于水电、火电等常规功率调节手段具有较大技术优势。电池储能电站跟踪负荷变化能力强，响应速度快，控制精确[4-5]。
随着锂离子电池持续使用，其容量将不断衰减，内阻将不断上升，从而降低电池的能量密度和功率密度，因此，有必要对电池的荷电状态(SOC)和健康状态(SOH)进行在线联合估算[6-11]。SOC的估算准确性受电池老化的影响。此外，若SOC的估计精度不高，则会影响电池的SOH校准精度，与电池SOC变化相比，电池SOH通常变化较慢。目前估算SOC的常用方法有安时积分法、开路电压法、卡尔曼滤波法、神经网络等。安时积分估算法简单可靠，充放电与所提供的电流有关，但是会对开环估计、不确定性或干扰引起的误差进行积累，并且对电流的要求很高，适用于对过充电不太敏感的系统[12-13]。开路电压法计算速度快，但需要电池达到稳定状态，这个过程需要很长时间，不适用于动态的电池SOC估算[14]。卡尔曼滤波法(KF)估算电池SOC要采用闭环估计，是最小均方的最优估算，扩展卡尔曼滤波(EKF)需要对非线性模型进行线性化处理，从而会使系统引入线性化误差，无迹卡尔曼滤波(UKF)存在估算不稳定的缺点，无法确定状态协方差的半正定性，不能降低噪声协方差带来的误差，估计精度会受到影响等[15-17]。神经网络法估算电池SOC时能很好地处理电池的复杂非线性特征，与卡尔曼滤波相比，神经网络法无需建立精确的电池等效电路模型，无需辨识模型参数，对于硬件精度要求不太高[18]。SOH定义为蓄电池满充容量相对额定容量的百分比，是衡量电池老化程度的度量指标，通常包括容量衰减或功率衰退。常用的指标包括电池容量、直流电阻和交流阻抗。SOH估算方法主要包括基于耐久性模型的开环方法和基于电池模型的闭环方法[19-21]。本文作者提出一种新的SOC和SOH估计策略，通过对锂离子电池实际运行过程中的输出电压测量值和所建立的仿真模型端口电压进行比较，利用PI控制器对所建立的电池模型欧姆内阻和开路电压进行修正，再根据SOC开路电压曲线获取SOC估算结果，并通过实验验证所提方法的有效性。
1 电池等效电路模型
目前锂离子电池的等效电路模型种类很多，其中二阶RC模型相对于一阶RC模型来说，准确度更高，而三、四阶RC模型计算量太大。因此，本文选用模型物理意义清晰、模型参数容易辨识的二阶RC等效电路模型，它能够很好地反映电池的静动态性能，也便于进行电池特性分析和参数辨识。
本文建立的模型如图1所示。图1中：i(t)为电池通过的电流；Ri为电池的欧姆内阻，在实际运行中会随SOC的变化而变化；Rts和Rtl分别为电池的极化电阻和浓差极化电阻；Cts和Ctl分别为电池的极化电容和浓差极化电容；VSOC为附加电阻Rsd两端的电压，表示SOC估算值乘以常数100；另一个电阻元件Rcap与电容Ccap串联，Rcap上的电压表征电池容量的降低程度，称为Peukert效应[22]；E0为受控电压源，两端电压为电池模型空载时的开路电压；Vmodel(t)为电池模型端口电压。
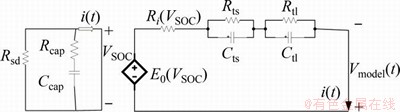
图1 锂离子电池电路模型
Fig. 1 Lithium battery circuit model
根据基尔霍夫定律，可以得到如下表达式：
(1)
(2)
式中：uctl和ucts为对应电容电阻上的电压。
状态空间方程为
(3)
(4)
式中：
(5)
(6)
(7)
(8)
(9)
常数m和n表征了E0和VSOC之间的线性关系。
2 基于实时电路模型的锂离子电池SOC和SOH联合估算方法
电池的荷电状态SOC和健康状态SOH对设计适当的电池管理系统(BMS)至关重要。本文结合PI控制器对电池内阻和SOC进行实时更新。总体的控制框图如图2所示，其中v(t)和i(t)分别为电池实际运行过程中测得的端口电压和电流。将v(t)与所搭建电路仿真模型中对应的电池端口电压Vmodel(t)进行比较，并由PI1控制器进行放大，提供模型开路电压校正项ΔE0，对当前开路电压E0.intial进行修正得到新的开路电压E0，再根据厂家提供的数据表SOC(E0)的关系来估计得到新的SOC估计值。将其与采用库仑计数法(CC)得到的SOC估计值进行比较，经过PI2控制器放大误差，输出附加项ΔVRi，结合当前模型欧姆内阻压降VRi.intial作为电池充放电期间模型欧姆内阻Ri输出的校正因子，ΔVRi表示内部欧姆电阻Ri的增量。
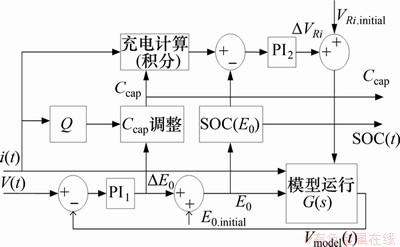
图2 实时SOC和SOH估算策略
Fig. 2 Real-time SOC and SOH estimation strategies
在s时域上，模型运行中的传递函数G(s)可以表示为
(10)
式中：
(11)
(12)
(13)
(14)
(15)
根据电荷守恒定律，锂离子电池在充电过程中受损耗，其容量Ccap会不断减少，而欧姆内阻会逐渐增大，不利于电池的正常运行。因此，当电池的容量减少到一定值时，需要及时进行更换。这两者都是变化缓慢的状态变量，与电池的SOH具有对应关系，所以，Ccap可以用于指示电池健康状况的变化情况。图2中SOC和SOH估算值可表示为：
(16)
(17)
式中：SOC(t0)为初始时刻的SOC估算值；Ccap_new为电池额定容量，电池实际容量Ccap则不断更新，Ccap与开路电压E0和电荷Q有关，函数关系如下式所示：
(18)
(19)
式中：
为t1时刻的附加电阻Rsol上的压降
；
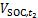为t2时刻的；
为t1时刻的开路电压E0；
为t2时刻的开路电压E0；电荷Q和开路电压降ΔE0需要通过单次或一系列的充放电操作确定。
在估算SOC和SOH的同时，需要实时更新电池管理系统状态和等效电路的参数。图2所示的控制策略可以分为2个子系统，每个子系统都与1个PI控制器相关，这样可以忽略它们之间的相互干扰，可以简单而有效地实现PI控制器的参数调整。
SOC(E0)是PI1及其闭环子系统的控制变量，其动态特性主要受Ccap，Rsd和与VSOC变化的影响。闭环传递函数Gcl1由式(20)给出，其中Gc1为PI控制器传递函数，Gss1为被控对象传递函数:
(20)
(21)
(22)
(23)
考虑到△VRi作为控制变量，可以对PI2进行类似分析。在这种情况下，系统动态性能主要受与电压响应有关的Ctl和Rtl参数的影响。
参考一个特定的工作点，SOC(E0)可以被视为一个恒定输入。根据所述的分析公式，Pa1，Pb1，Pa2和Pb2为常数，将每个PI控制器的增益kp和ki计算为线性系统的代数解，从而计算得到合适的控制器参数：
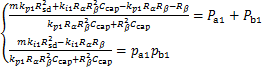(24)
(25)
式中：
和
为PI1控制器的比例积分参数；
和
为PI2控制器的比例积分参数。
3 实验验证
本文实验对象为磷酸铁锂离子单体电池，电池额定电压为12 V，额定容量为7.12 A·h，其中PI控制器的参数kp1和kp2为0.1，ki1和ki2为1，而在实际的操作过程中需要根据式(24)和(25)进行微调。
在工作温度为20 °C，SOH为83%时，电池随机充放电过程中的电流和采用扩展卡尔曼滤波法(EKF)、库仑计数法(CC)和本文所提方法SOC估算值对比曲线见图3、图4和图5。当SOH为80%时，充电过程中采用扩展卡尔曼滤波法(EKF)、库仑计数法(CC)和本文所提方法获得的SOC估算值对比曲线见图6。从图4~6可见：在电池充放电过程中，采用所提出的方法所得SOC估算值与采用EKF所得的SOC估算值在长时间内相近，但在初始估算过程中，SOC的估算误差明显降低；而采用库仑计数法(CC)时，由于完全忽略了电池老化的因素，即SOH约等于100%，在SOC的估算过程中会对误差进行积累，导致SOC的曲线偏离实际值；与CC法的最终收敛偏离不同，EKF和本文所提方法会收敛到更准确的SOC估计值。为了更有效地评估所提出的方法是否能够模拟SOH在寿命周期中的变化，通过不断重复电池充放电周期实验，每个周期在环境温度为20 °C的情况下对电池进行完整地充放电，所得SOH估计值如图7所示。结果表明，本文所提的SOH估算值精度更高。
图3 SOH为83%时锂离子电池冲放电电流曲线
Fig. 3 Impulse discharge current curve of lithium-ion battery when SOH is 83%
图4 SOH为83%时锂离子电池放电过程SOC估算曲线
Fig. 4 SOC estimation curve of lithium-ion battery during discharge when SOH is 83%
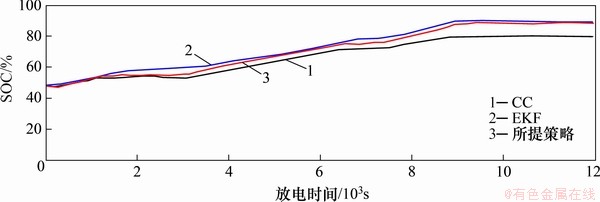
图5 SOH为83%时锂离子电池充电过程SOC估算曲线
Fig. 5 SOC estimation curve of lithium-ion battery charging process when SOH is 83%
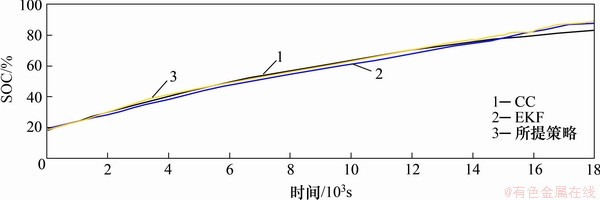
图6 SOH为80%时锂离子电池充电过程SOC估算曲线
Fig. 6 SOC estimation curve of lithium-ion battery charging process when SOH is 80%
图7 SOH估算曲线
Fig. 7 SOH estimation curves
4 结论
1) 以二阶RC电路作为电池等效电路模型，较大程度上简化了电池特性变化的分析过程，具有实际应用效果。
2) 提出一种新的锂离子电池状态估算方法，其中SOC和SOH由合适的算法确定。结合PI控制器，对电池电压的测量值和计算值进行实时比较，比较结果可用于适时调整锂离子电路模型的主要参数，以补偿由于模型不精确导致的SOC和SOH估算误差。该方法具有精度高、能够实现SOC和SOH的在线估计等优点。实验结果验证了所提策略的有效性。
参考文献：
[1] TIE Siangfui, TAN Chewei. A review of energy sources and energy manage-ment system in electric vehicles[J]. Renewable and Sustainable Energy Reviews, 2013, 20: 82-102.
[2] XIA Xiangyang, ZHAO Xinxin, ZENG Heqing, et al. A novel design of hybrid energy storage system for electric vehicles[J]. Chinese Journal of Electrical Engineering, 2018, 4(1): 45-51
[3] 夏向阳, 孔祥霁, 帅智康, 等. 基于磁集成结构DC-DC变换器的超级电容储能系统[J]. 电力自动化设备, 2014, 34(11): 95-99.
XIA Xiangyang, KONG Xiangji, SHUAI Zhikang. Super-capacitor energy storage system based on DC-DC converter with inte grated magnetic structure[J]. Electric Power Automation Equipment, 2014, 34(11): 95-99.
[4] 李建林, 王上行, 袁晓冬, 等. 江苏电网侧电池储能电站建设运行的启示[J]. 电力系统自动化, 2018, 42(21): 1-9.
LI Jianlin, WANG Shangxing, YUAN Xiaodong, et al. Enlightenment from construction and operation of battery energy storage station on grid side in Jiangsu power grid[J] Automation of Electric Power Systems, 2018, 42(21): 1-9.
[5] 陈徽, 刘世林, 汝改革. 配电网中分布式储能系统的优化配置[J]. 四川理工学院学报(自然科学版), 2018, 31(6): 39-45.
CHEN Hui, LIU Shilin, RU Gaige. Optimal allocation of distributed energy storage system in distribution network[J]. Journal of Sichuan University of Science and Engineering(Natural Science Edition), 2018, 31(6): 39-45.
[6] LI C, XIAO F, FAN Y. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit[J]. Energies 2019, 12: 1592.
[7] DAI H, ZHAO G, LIN M, et al. A novel estimation method for the state of health of lithium-ion battery using prior knowledge-based neural network and Markov chain[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7706-7716.
[8] WANG Z, ZENG S, GUO J, et al. State of health estimation of lithium-ion batteries based on the constant voltage charging curve[J]. Energy, 2019, 167: 661-669.
[9] 王跃飞, 黄磊, 舒成才, 等. 车载铅酸蓄电池SOC和SOH的在线估算[J]. 农业装备与车辆工程, 2017, 55(10): 19-24.
WANG Yuefei, HUANG Lei, SHU Chengcai, et al. Research on SOC and SOH estimation of vehicle lead-acidbattery[J]. Agricultural quipment and Vehicle Engineering, 2017, 55(10): 19-24.
[10] BELT J, UTGIKAR V, BLOOM I. Calendar and PHEV cycle life aging of high-energy, lithium-ion cells containing blended spineland layered-oxide cathodes[J]. Journal of Power Sources, 2011, 196(23): 10213-10221.
[11] 隋欣, 陈永翀, 张晓虎, 等. 基于改进滑模观测器的锂离子电池荷电状态估计方法[J]. 电工电能新技术, 2018, 37(12): 73-82.
SUI Xin, CHEN Yongchong, ZHANG Xiaohu. Improved sliding mode observer for state of charge estimation of lithium-ion battery[J]. Advanced Technology of Electrical Engineering and Energy, 2018, 37(12): 73-82.
[12] 徐尖峰, 张颖, 甄玉, 等. 基于安时积分法的电池SOC估算[J]. 汽车实用技术, 2018, 23(18): 9-11.
XU Jianfeng, ZHANG Ying, ZHEN Yu, et al. Lithium-ion battery SOC estimation based on Ahh-total integration metho [J]. Automobile Applied Technology, 2018, 23(18): 9-11.
[13] PILLER S, PERRIN M, JOSSEN A. Methods for state-of-charge determination and their applications[J]. Journal of Power Sources, 2001, 96(1): 113-120.
[14] ZHANG Fei, LIU Guangjun, FANG Lijin, et al. Estimation of battery state of charge with, observer: applied to a robot for inspecting power transmission lines[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 1086-1095.
[15] CHEN Jian, OUYANG Quan, XU Chenfeng, et al. Neural network-based state of charge observer design for lithium-ion batteries[J]. IEEE Transactions on Control Systems Technology, 2018, 26(1): 313-320.
[16] MA Yan, DUAN Peng, SUN Yanshuai, et al. Equalization of lithium-ion battery pack based on fuzzy logic control in electric vehicle[J]. IEEE Transactions on Industrial Electronics, 2018, 65(8): 6762-6771.
[17] SAHINOGLU G O, PAJOVIC M, SAHINOGLU Z, et al. Battery state-of-charge estimation based on regular/recurrent Gaussian process regression[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 4311-4321.
[18] SBARUFATTI C, CORBETTA M, GIGLIO M, et al. Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks[J]. Journal of Power Sources, 2017, 344: 128-140.
[19] FOTOUHI A, AUGER D J, PROPP K, et al. Lithium-sulfur battery state-of-charge observability analysis and estimation[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5847-5859.
[20] MENG Jinhao, RICCO M, LUO Guangzhao, et al. An overview of online implementable SOC estimation methods for Lithium-ion batteries[C]// 2017 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM) & 2017 Intel Aegean Conference on Electrical Machines and Power Electronics(ACEMP). Brasov, Romania: IEEE, 2017: 573-580.
[21] GUHA A, PATRA A, VAISAKH K V. Remaining useful life estimation of lithium-ion batteries based on the internal resistance growth model[C]// 2017 Indian Control Conference(ICC). Guwahati, India: IEEE, 2017: 33-38.
[22] DOERFFEL D, SHARKH S A. A critical review of using the Peukert equation for determining the remaining capacity of lead-acid and lithium-ion batteries[J]. Journal of Power Sources, 2006, 155(2): 395-40.
(编辑 陈灿华)
收稿日期： 2020 -08 -10; 修回日期： 2020 -10 -22
基金项目(Foundation item)：国家自然科学基金资助项目(51977014) (Project(51977014) supported by the National Natural Science Foundation of China)
通信作者：夏向阳，博士，教授，博士生导师，从事储能系统安全控制和柔性直流输电控制等研究；E-mail: xia_xy@126.com
引用格式：陈霖华, 陈剑, 徐志强, 等. 基于实时电路模型的储能系统锂离子电池状态估算[J]. 中南大学学报(自然科学版), 2021, 52(2): 458-464.
Citation:CHEN Linhua, CHEN Jian, XU Zhiqiang, et al. State estimation of lithium ion battery in energy storage system based on real time circuit model[J]. Journal of Central South University(Science and Technology), 2021, 52(2): 458-464.
