多个体系统编队分布式控制的循环追踪算法

杨希祥，杨涛，杨慧欣，张为华

(国防科学技术大学 航天科学与工程学院，湖南 长沙，410073)

摘要：系统总结循环追踪算法演进过程，建立和推导二维平面循环追踪算法模型，包括线性循环追踪、定速非线性循环追踪、变速非线性循环追踪等，并结合数值仿真，对上述3种循环追踪算法性质和特点进行分析。研究结果表明：线性循环追踪中，个体均以对数螺旋曲线轨迹收敛于初始几何中心，定速非线性循环追踪中，个体收敛于以初始几何中心为圆心的圆上；变速非线性循环追踪中，系统最终状态与控制增益有关。

关键词：多体系统；编队控制；循环追踪算法

中图分类号：TP273          文献标志码：A         文章编号：1672-7207(2014)02-0450-07

Cyclic pursuit algorithm for distributed formation control of multi-agent systems

YANG Xixiang, YANG Tao, YANG Huixin, ZHANG Weihua

(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)

Abstract: The development course of cyclic pursuit algorithm was summarized, and the mathematical model of cyclic pursuit was established and deduced, including linear cyclic pursuit, fixed-speed nonlinear cyclic pursuit and variety-speed nonlinear cyclic pursuit. The property of these three algorithms was analyzed with numerical simulation. The results show that all agents meet at the initial geometrical center in linear cyclic pursuit. Agents finally distribute on a circle whose center is the initial geometrical center in fixed-speed nonlinear cyclic pursuit, and final state of agents in variety-speed nonlinear cyclic pursuit is decided by control gain.

Key words: multi-agent system; formation control; cyclic pursuit algorithm

长久以来，自然界的群体行为受到学术界广泛关注和研究，并在军事作战、航空航天、工业生产等诸多工程领域逐步得到应用，如多机器人编队执行侦察、巡逻等任务，多颗卫星编队飞行执行对地观测任务及多无人飞行器编队飞行执行攻击任务等。大量研究表明，多个体系统协同工作使很多单个个体难以实现的任务变得简单，多功能得以实现，系统整体性能得到极大提升。编队控制是多个体系统编队完成任务必须解决的关键问题。编队控制主要内容包括队形生成、队形保持、队形重构等。编队控制算法是编队控制的核心。国内外学者对此进行了积极研究^[1-2]。编队控制需设计合理的控制结构和控制策略。控制策略分为集中控制和分布式控制。相对集中式控制，分布式控制更具优势，目前，学者们已提出了多种分布式控制律。研究人员从生物运动中个体相互追踪的行为出发，总结出基于循环矩阵的循环追踪运动策略，提出将循环追踪算法应用于编队分布式控制的新思想，并将其应用于机器人、无人机等编队控制^[3-4]。目前，国内外关于循环追踪算法尤其是其工程领域应用的研究较少。为此，本文作者对循环追踪算法的历史演进进行系统阐述，对典型循环追踪模型进行推导，结合数值仿真，对算法的特点与性质进行深入分析，为循环追踪算法理论研究和工程应用提供理论参考。

1  循环追踪算法演进过程

1.1  经典追踪算法(classic pursuit algorithm，ClaPA)

循环追踪算法源于经典追踪算法。追踪的思想源于数学上的追踪曲线。追踪曲线的定义可简要描述为，如果空间中一点q沿已知曲线运动，点p始终指向q并以相同速率运动，点p的运动轨迹即为追踪曲线，这也是所谓的经典追踪问题。学术界普遍认为法国数学家Bouguer首次研究了经典追踪问题(1732年)，事实上，早在1672—1676年，Perrault就提出了追踪曲线的问题^[5]。

1748年，Ash首先描述了圆形追踪问题：1只蜘蛛追踪沿半圆形玻璃运动的苍蝇。但直到1859年，同类问题才再次被提及，但没有学者给出这一问题的解。1920年，Hathaway在《American Mathmatical Monthly》中重新描述了圆形追踪问题，“圆形池塘中央的一只小狗，追踪沿池塘边运动的鸭子，狗与鸭子的运动速率为n:1，则小狗将按何种曲线运动？”。后来的研究表明：当速率比n＞1时，追踪者最终可赶上目标；当速率比n=1时，追踪者与目标具有相同运动轨迹，且稳定后位移差和相位差保持不变；当速率比n＜1时，追踪者的运动轨迹为一有限圆，其与目标的运动半径比为n(见图1^[16])。上述结果也反映了经典追踪问题的一个共性规律，即只有当追踪者速度大于被追踪者时才能捕获目标。

由经典追踪问题衍生的经典追踪算法在导弹、鱼雷等攻击机动目标的工程问题中得到研究和应用。

1.2  线性循环追踪算法(linear cyclic pursuit algorithm，LCyPA)

1877年，法国数学家Lucas首次正式提出了循环追踪问题：3只小狗分别位于平面内等边三角形的顶点，依次追踪，其运动将形成怎样的轨迹？3月以后，Brocard回答了这一问题：若3只小狗同时以等速追踪，每只小狗的追踪曲线均为对数螺旋曲线，且3只小狗最终交会于三角形内1点，即著名的Brocard点^[5-6]。

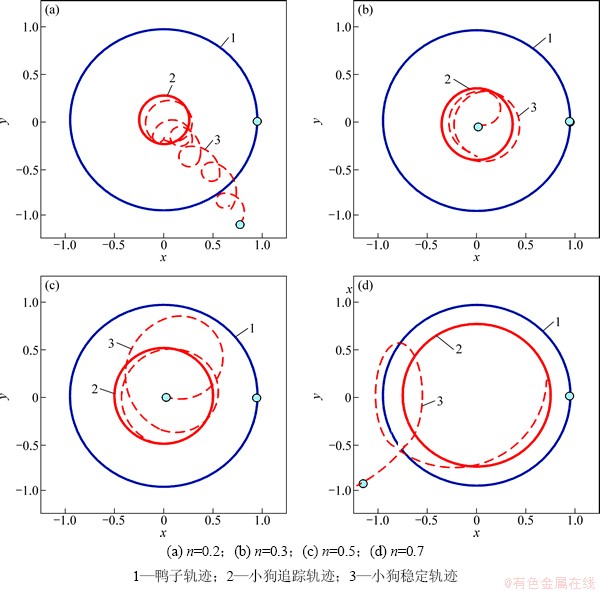
图1  不同速率比下圆形追踪问题结果

Fig. 1  Results for circle pursuit with different speed ratio

1908年，Hackett采用数值分析方法研究了循环追踪问题的微分方程，他没有采用等边三角形的限制条件。1918年，Bateman在教材中提到了非对称的3只小狗循环追踪问题。在1950前，循环追踪算法只是为数学家所熟知。1965年，Gardner在《Scientific American》杂志上开设了专栏，这一领域的研究才逐渐为其余领域所了解。在1962年，Clapham已将3只小狗问题扩展为一般性的n只小虫问题^[7]，即n只小虫位于正n边形的顶点，这也是循环追踪领域极为著名的问题。后来的研究表明，如果每只小虫均以相同速度依次追踪其下一个数目对n取模的编号的小虫，则所有小虫的运动轨迹均为对数螺旋曲线，且最终交会于多边形的中心。1969年，Watton 和Kydon提供了正多边形问题的解，指出常速度假设不是必要的。许多学者对生物领域的追踪现象进行了研究，发现许多动物，如蚂蚁、蟋蟀、蜜蜂等，都存在类似循环追踪的行为。1971年，Klamkin和Newman研究了小虫不在正多边形顶点的情况，研究结果表明，只要小虫初始队形不在同一条直线上，最终都将在1点处相遇。对于3只小虫位于非等边三角形顶点的情况，推导得出每只小虫的速度与三角形边长关系的表达式^[8]。

1991年，Bruckstein等分析了规则和不规则多边形初始位置、连续(以蚁群为对象)和离散的(以蟋蟀群和青蛙群为对象)追踪形式、匀速和变速的循环追踪问题。Smith等采用多层结构加速循环追踪的收敛速度。Sinha和Ghose将线性循环追踪问题推广到个体具有不同控制增益的情况。

上述传统的循环追踪问题都是基于质点模型假设，追踪者速度方向实时指向被追踪者，不考虑实际能量限制或速度转向的时间延迟引起的非线性，因此，在追踪领域一般称为线性循环追踪(linear cyclic pursuit algorithm，LCyPA)。在实际工程问题中，转动控制能量往往不足以达到LCyPA要求，或需要一定反应时间才能完成速度方向指向目标的要求，LCyPA模型则不再适合准确描述个体的运动，非线性循环追踪 (Nonlinear Cyclic Pursuit，NlCyP)模型与算法应运而生。

1.3  非线性循环追踪算法(linear cyclic pursuit algorithm，LCyPA)

随着轮载机器人编队控制研究的蓬勃开展，循环追踪算法研究扩展到非线性范围，因为轮载机器人调整速度方向存在时间延迟。

Marshall等^{[3, 9]}对非线性循环追踪算法进行了大量研究，提出了采用相对运动方式描述非线性循环追踪行为的模型，将追踪方式扩展到非相邻成员的范围，研究表明，包含所有成员的闭合信息交流环是产生统一构形的必要条件，他们还采用一组独轮机器人进行了半实物仿真实验，证明了非线性循环追踪算法对工程问题的适用性。

Krishnaprasad等对非循环追踪算法在自主移动机器人中的应用进行了大量研究。Zhang等研究了平面内多个体序贯追踪问题，其中体现了循环追踪的思想；Gehrels^[10]以地面轮载机器人为例，对非线性循环追踪算法进行了半实物仿真；Galloway^[11]对循环追踪算法的几何特性、数学原理等进行了深入系统研究。

此外，东京大学等也在非线性循环追踪领域开展了理论与试验研究^[12]。Hara等^[13]研究了三维空间多个体系统编队循环追踪控制问题；Jaime^[14]对基于循环追踪方法的三维空间卫星编队分布式控制进行了深入研究，提出一种特征分解方法，对循环追踪方法进行了改进，并采用SPHERES试验系统进行了验证，还采用其解决电磁编队卫星编队控制问题。

2  线性循环追踪模型

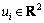考虑二维空间中存在的一组n个体编队，个体坐标由表示，t≥0。若对任一个体施加控制，使之追踪个体i+1，i=1，2，…，n，追踪对象以n取模 (简记为 modn)。系统控制可统一描述为

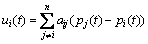         (1)

式中，a_ij表示个体i 受个体j影响的控制增益；i，j=1，2，…，n。全系统可表示为如下形式：

              (2)

式中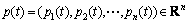：；A为系数矩阵。

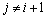若循环追踪控制中，个体i的运动仅受个体i+1作用，即式(2)描述的系统中，当j=i+1时，；当且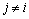时，a_ij=0；i=1，2，…，n。此时，直接指向成员i+1的控制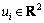变为

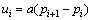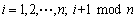；  (3)

式中，a为常数。个体运动学方程为：

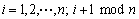；  (4)

以向量形式表示为

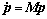                                (5)

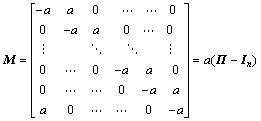  (6)

式中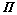：为基本循环矩阵；I_n为n阶单位矩阵。此种追踪方式表示“一对一”线性循环追踪运动控制，信息交流机制相对简单，更利于工程应用与实现。

3  非线性循环追踪模型

以单轮机器人类型的非完整约束系统为例，其运动方程一般表示为

               (7)

式中，表示个体在平面内的位置；θ表示运动方向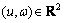；表示切向速度和角速度控制输入。式(7)描述个体运动简单直观，但不便描述需要的追踪控制律。为此，引入在相对坐标系下描述非线性循环追踪问题的方式^[9]。系统中含2个成员和3个成员时，循环追踪的相对运动描述如图2所示。图2中：r_i表示个体i与i+1的距离；α_i表示个体i实际速度方向与期望速度方向的夹角；β_i表示个体i实际速度反方向与个体i+1速度方向的夹角。

个体i的运动方程可表示为

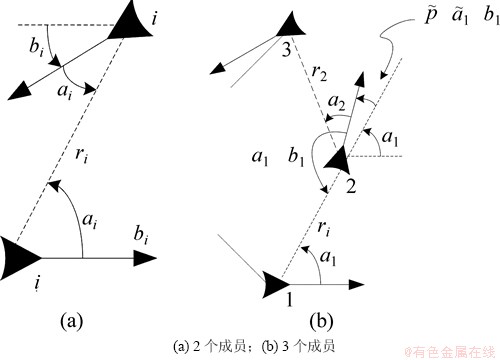
图2  两成员和三成员循环追踪相对坐标

Fig. 2  Relative coordinate in cyclic pursuit for two agents and three agents

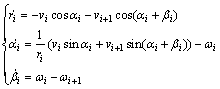  (8)

对于包含n个成员的多个体系统，成员相对坐标，i=1，…，n。式(8)定义的多个体系统相对运动方程存在如下关系：

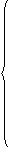
 (9)

(1) 若对个体运动施加控制：

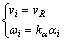                                  (10)

式中：k_α为常数控制增益，k_α＞0，v_R＞0，由于速度控制量为定值，因此，称为定速的非线性循环追踪算法，此时，式(8)转化为

          (11)

(2) 若对个体运动施加控制：

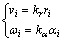                                   (12)

式中：k_r＞0；k_α＞0，为常数控制增益，由于速度控制量为随相对距离变化的变量，因此，称为变速的非线性循环追踪算法，此时，式(8)转化为

    (13)

4  仿真结果与分析

4.1  线性循环追踪仿真分析

分别以3个体系统和5个体系统为例，对线性循环追踪进行仿真。任意设定个体初始位置，个体依次按逆时针追踪。3个体循环追踪仿真时，初始位置分别取为(3, 5)，(0, 0)，(6. 0)， 5个体循环追踪仿真时，初始位置分别取为(2, 7)，(0, 3)，(4. 0)，(7. 3)，(4. 7)，a取为2.0。仿真结果如图3和图4所示，图中，横、纵坐标分别表示x向位置和y向位置，已进行无量纲化处理(下同)。

由图3和4可以看出：无论是3个体系统，还是5个体系统，在线性循环追踪中，个体均以对数螺旋曲线运动收敛于初始几何中心，且个体运动轨迹均为逆时针环绕。事实上，这一性质对n个体系统均成立。

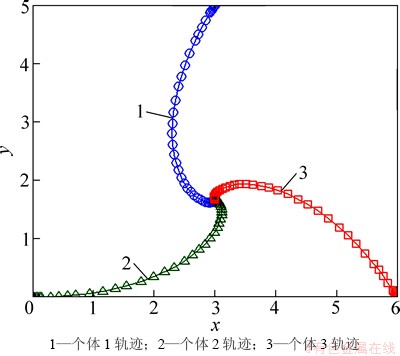
图3  3个体线性循环追踪结果

Fig. 3  Linear cyclic pursuit results for 3 agents

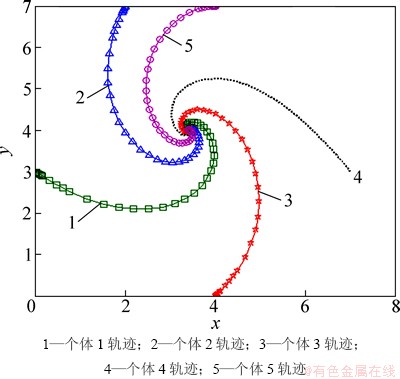
图4  5个体线性循环追踪结果

Fig. 4  Linear cyclic pursuit results for 5 agents

4.2  定速的非线性循环追踪仿真分析

以3个体系统为例，对定速的非线性循环追踪进行仿真分析。

个体初始位置取为(2, 2)，(0, 0)，(1.5. 0)，个体按序列编号顺次追踪，追踪速度相同，均取为1.0，控制增益k_α分别为1.0，3.0，5.0，7.0，仿真结果如图5所示。由图5可以看出，3个体最终分布于以初始几何中心为圆心、半径相同的圆上；随k_α增大，最终形成的圆形轨迹中心不变，半径逐渐减小。这是因为随控制增益增大，个体运动方向调整速度加快，逐步接近线性循环追踪情形。

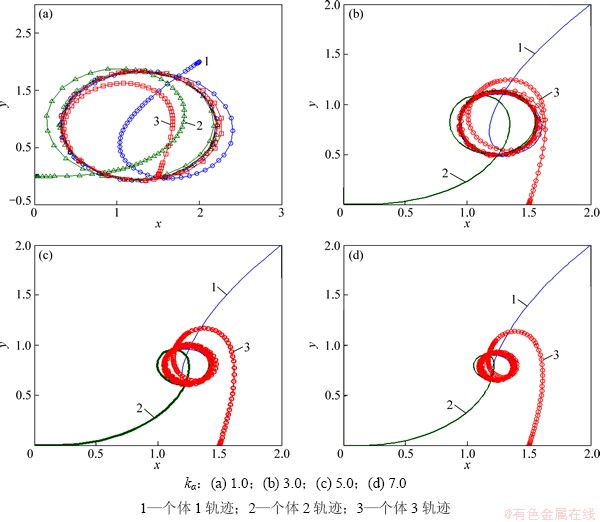
图5  定速非线性循环追踪结果

Fig. 5  Results for fixed-speed nonlinear cyclic pursuit

4.3  变速的非线性循环追踪仿真分析

以3个体系统为例，对变速的非线性循环追踪进行仿真分析。个体初始位置取为(6, 2)，(0, 0)，(1.5. 0)，个体按序列编号顺次追踪，追踪速度相同，不失一般性，控制增益k_α取为1.0，k_r分别取0.3，0.6，0.9，仿真结果如图6所示。

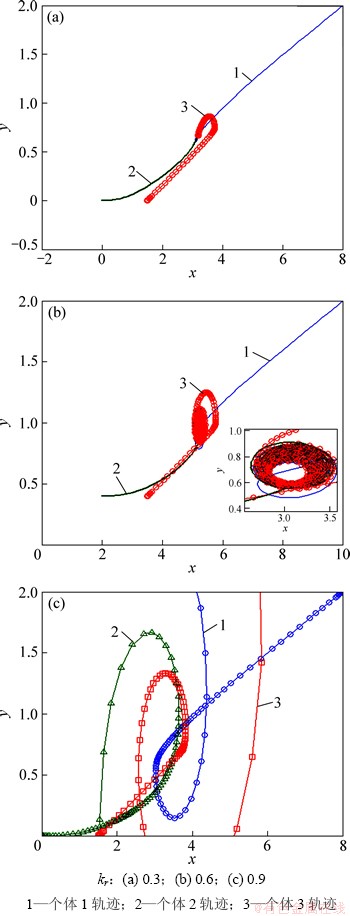
图6  变速非线性循环追踪结果

Fig. 6  Results for variety-speed nonlinear cyclic pursuit

由图6可以看出：系统最终状态与k_r取值有关；当k_r较小时，系统收敛于初始几何中心；当k_r增大到一定值时，系统收敛于以初始几何中心为圆心、半径相同的圆上；当k_r继续增大到一定值时，系统发散。因此，在变速的非线性循环追踪中，控制增益的合理选取尤为重要。

需要特别说明的是：上述关于各种循环追踪算法的仿真结果表明了一个重要性质，即多个体系统采用循环追踪控制策略时，系统收敛的中心就是其初始几何中心，与运动过程无关。

5  结论

(1)首次对循环追踪算法的演进过程进行了系统总结。分别建立和推导了线性循环追踪、定速非线性循环追踪和变速非线性循环追踪算法模型。

(2) 线性循环追踪中，个体均以对数螺旋曲线轨迹收敛于初始几何中心；定速非线性循环追踪中，个体收敛于以初始几何中心为圆心、半径相同的圆上，且最终形成圆的半径由角度控制增益决定；变速非线性循环追踪中，系统最终状态与k_r有关，随k_r逐渐增大，系统经历由收敛于初始几何中心、收敛于以初始几何中心为圆心的圆上和发散的不同状态。

(3) 循环追踪算法只需获取个体局部信息，便可实现对系统的全局控制，是具有独特优势和广阔应用前景的新方法。下一步将研究其在卫星编队飞行控制中的应用。

参考文献：

[1] Desai J P, Ostrowski J P, Kumar V. Modeling and control of formations of nonholonomic mobile robots[J]. IEEE Transactions on Robotics and Automation, 2001, 17(6): 905-908.

[2] Rahmani A, Ji M, Mesbahi M, et al. Controllability of multi-agent systems from a graph-theoretic perspective[J]. SIAM Journal on Control and Optimization, 2009, 48(1): 162-186.

[3] Marshall J A, Broucke M E, Francis B A. Formations of vehicles in cyclic pursuit[J]. IEEE Transactions on automatic control, 2004, 49(11): 1963-1974.

[4] Gehrels T, Helum C, Rahul K, et al. Study of nonlinear cyclic pursuit strategies applied to MAV swarms[R]. Bangalore: Indian Institute of Science, Department of Aerospace Engineering, 2011: 9-12.

[5] Nahin P J. The mathematics of pursuit and evasion[M]. Princeton: Princeton University Press, 2007: 23-24.

[6] 杨涛. 面向空间任务的追踪理论与应用研究[D]. 长沙: 国防科学技术大学航天与材料工程学院, 2010: 7-8.

YANG Tao. Research on pursuit theory and its application to space mission[D]. Changsha: National University of Defense Technology, College of Aerospace and Materials Engineering, 2010: 7-8.

[7] Clapham J C. Playful mice[J]. Recreational Mathematics Magazine, 1962, 22(8): 6-7.

[8] Klamkin M S, Newman D J. Cyclic pursuit or 'the three bugs problem[J]. American MathematIcal Monthly, 1971, 40(6/7): 631-639.

[9] Marshall J A. Coordinated autonomy: Pursuit formations of multivehicle systems[D]. Toronto: University of Toronto. Department of Electrical and Computer Engineering, 2005: 5-10.

[10] Gehrels T. Pursuit techniques on pioneer robots[R]. Maryland: University of Maryland, Institute for Systems Research, 2007: 8-16.

[11] Galloway K S. Cyclic pursuit: Symmetry, reduction and nonlinear dynamics[D]. Maryland: University of Maryland, Institute for Systems Research, 2011.

[12] Kim T H, Hara S, Hori Y. Stabilization of multi-agent dynamical systems for cyclic pursuit behavior[R]. Tokyo: University of Tokyo. School of Information and Science and Technology, 2009: 10-13.

[13] Hara S, Kim T H, Hori Y. Distributed formation control for target-enclosing operations by multiple dynamics agents based on a cyclic pursuit strategy[R]. Tokyo: University of Tokyo. School of Information and Science and Technology, 2007: 7-15.

[14] Jaime L. New decentralized algorithms for spacecraft formation control based on a cyclic approach[D]. Massachusetts: Massachusetts Institute of Technology, Department of Aeronautics and Astronautics, 2010.

(编辑  赵俊)

收稿日期：2013-05-20；修回日期：2013-08-30

基金项目：国家自然科学基金资助项目(11102229)

通信作者：杨希祥(1982-)，男，河北阜城人，博士，讲师；从事飞行器动力学与控制研究；电话：0731-84576446；E-mail：nkyangxixiang@163.com