非线性不确定时滞系统的鲁棒保成本弹性滤波
谢立1,葛浩宇1,史勇强2,陈耀武2
(1. 浙江大学 信息与电子工程系,浙江 杭州,310027;
2.浙江大学 仪器科学工程系,浙江 杭州,310027)
摘要:针对一类含有非线性不确定项的时变时滞不确定参数系统,研究鲁棒保成本弹性滤波器设计问题。非线性不确定项满足范数有界条件,且同时存在于系统模型和量测输出,系统参数不确定性满足广义匹配条件,并采用加型滤波增益变化来反映滤波器实现过程中的不精确性。将弹性滤波器的设计问题归结为一个线性矩阵不等式组(LMI)问题,通过求解这个LMI问题可以获得滤波器参数。
关键词:非线性不确定系统; 鲁棒保成本弹性滤波; 线性矩阵不等式; 时变时滞; 凸优化
中图分类号:TP13 文献标志码:A 文章编号:1672-7207(2011)S1-0355-05
Robust guaranteed cost resilient filtering for nonlinear uncertain systems with time delay
XIE Li1, GE Hao-yu1, SHI Yong-qiang2, CHEN Yao-wu2
(1. Department of Information and Electronic Engineering, Zhejiang University, Hangzhou 310027, China;
2. Department of Instruments Science and Engineering, Zhejiang University, Hangzhou 310027, China)
Abstract: The problem of robust guaranteed cost resilient filtering design for nonlinear uncertain systems with time-varying delays is investigated. The nonlinear uncertainties are assumed to satisfy the norm-bounded conditions, and the uncertainties exit in both the system model and measurement output. The resilient filtering to be designed has multiplicative filter gain variations. The considered system is assumed to have norm-bounded parameters uncertainties. By using Lyapunov stability theory, the robust guaranteed cost resilient filtering design problem is represented in terms of linear matrix inequality (LMI). The parameters of the filter can be obtained by solving the LMI.
Key words: nonlinear uncertain systems; robust resilient filtering guaranteed cost; linear matrix inequality; time varying delay; convex optimization
近年来,关于不确定动态系统鲁棒滤波的研究得到了很大的发展。传统的Kalman滤波理论已经不能够解决日益复杂的实际不确定动态系统的滤波问题。为了解决不确定系统滤波器设计中出现的误差发散与模型精确化之间的矛盾,在过去的10年中,研究者从各种不同的角度研究了鲁棒滤波问题,并获得了许多有意义的研究结果。为了考察滤波器设计的性能,常需要在某个评价指标的约束下设计,即通过设计一个滤波器结构来估计输出误差信号,在此基础上最小化某个性能标准。在这种设计理念下,Xie等[1]设计了Kalman滤波使得一类含有范数有界参数不确定项的不确定系统的估计误差协方差满足一定上界;Shaked等[2]研究最小方差滤波设计方法;Petersen等[3]提出了保成本滤波器设计方法。一些传统的滤波器设计方法较少考虑滤波器实现过程中出现的不确定因素,如A/D转化对滤波精度的影响、有限字长效应和量化误差等可能导致滤波器性能变差等情况,因此,在滤波器的设计过程中必须充分考虑到滤波不确定性等[4]。现实系统中由传输、测量、反应等产生的时滞现象,往往会引起系统不稳定或使系统性能变差。时滞的存在也为滤波器的设计带来的困难,令滤波设计更加复杂。Mahmoud[5]介绍了时滞系统弹性滤波器的设计方法。Yang等[6]将弹性滤波的研究结果进一步推广到了鲁棒H∞滤波器设计中。当所研究的系统为非线性系统时,关于线性系统的一些滤波研究结论将不再适用。值得注意的是,目前有关于在量测信号中含有非线性不确定项的非线性不确定参数时滞系统鲁棒弹性滤波器设计的研究报道还不多。为此,本文作者利用线性矩阵不等式(LMI)理论分析系统模型、量测输出和评估输出中同时含有时变时滞和参数不确定性,以及系统模型和量测输出中同时含有非线性项的不确定连续系统鲁棒弹性保成本滤波器设计问题。
1 系统描述
考虑如下非线性不确定时滞连续系统:
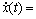


 ;
;


 ;
;
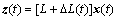

 ,
, 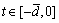 (1)
(1)
其中: 为系统状态矢量;
为系统状态矢量; 为量测输出矢量;
为量测输出矢量; 为评价输出矢量;
为评价输出矢量; 为初值函数。
为初值函数。
A(t),Ad(t),B(t),C(t),Cd(t),D(t),L(t)和Ld(t)为适维实参数矩阵; ,
, ,
, ,
, ,
,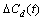 ,
,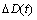 ,
, 和
和 为时变参数不确定项,满足下列广义匹配条件:
为时变参数不确定项,满足下列广义匹配条件:


 (2)
(2)


 (3)
(3)
 为未知矩阵,定义如下:
为未知矩阵,定义如下:
 ,
,  ,
,  中的元
中的元
素Lebesgue可测} (4)
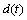 为时变时滞,满足条件:
为时变时滞,满足条件:
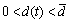 ,
,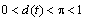 (5)
(5)
 和
和 为系统未知非线性项,满足下列范数有界条件:
为系统未知非线性项,满足下列范数有界条件:
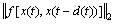

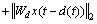 (6)
(6)


 (7)
(7)
本文将设计具有下列结构的弹性动态滤波器:

 ;
; (8)
(8)
其中: ;
; 和
和
 分别为待定滤波器增益参数;
分别为待定滤波器增益参数; ,
,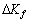 和
和 为加型滤波器增益变化。满足:
为加型滤波器增益变化。满足:
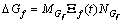 ;
; ;
;
 ;
;
 ,
,  (9)
(9)
定义滤波误差矢量 (t)=
(t)=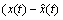 和评价误差
和评价误差
 (t)=
(t)= 如下:
如下:

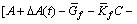
 +
+

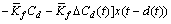 +
+

 ;
;


 +
+

 (10)
(10)
于是,建立下列增广滤波误差系统:


 +
+

 ;
;


 ;
;
 ,
,  (11)
(11)
其中: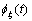 为滤波误差系统初值函数;
为滤波误差系统初值函数;
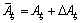 ;
; 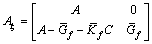 ;
;
 ;
;
 ;
; 
 ;
;
 ;
;
 =
=

 ;
;
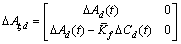 =
=

 ;
;

 ;
;
 ;
; 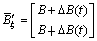 ;
;
 ;
; 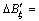



 =
=
 ;
;
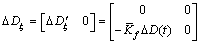 =
=
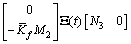
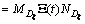 ;
;
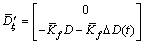 ;
;  ;
;

 ;
;
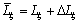 ;
;  ;
;
 ;
;  ;
;


 ;
;


 ;
;
 ;
;
 (12)
(12)
根据条件(5)和(6),有下列关系:


 (13)
(13)


 (14)
(14)
其中:
 ,
, 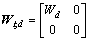 ,
,
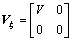 ,
, 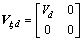 (15)
(15)
定义二次型保成本性能测度函数如下:
 (16)
(16)
本文的研究目标是:确定弹性滤波器(式(8))中的滤波器参数Gf,Kf和Lf,使得滤波器渐近稳定,同时令滤波误差动态系统(式(10))的保成本上界值最小。
2 主要结果
这里首先给出保成本弹性滤波器存在的充分 条件。
定理1:考虑滤波误差动态系统(式(10)),若存在一个正数J*满足 ,以及正定矩阵P和R,使得对于任何容许时变时滞(式(7)),下列线性矩阵不等式成立
,以及正定矩阵P和R,使得对于任何容许时变时滞(式(7)),下列线性矩阵不等式成立
 (17)
(17)
其中:
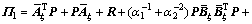



 ;
;

则滤波器(式(8))为满足保成本性能测度约束的鲁棒保成本弹性滤波器。
下面,我们给出保成本弹性滤波器凸优化设计方法,即通过求解一组满足优化指标的线性矩阵不等式,获得满足保成本上界最小的鲁棒滤波器参数。
定理2:考虑滤波误差动态系统(式(11)),以及保成本性能函数(式(16)),若下列凸优化问题:
Min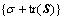 (18)
(18)
s.t.
 ;
; 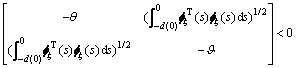 ;
;
 ;
; 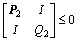 ;
;
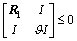 ;
;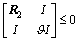 ; (19)
; (19)
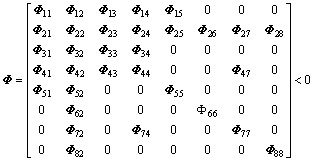 (20)
(20)
其中:


 +
+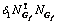

 ;
;

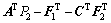 -
- ;
;
 ;
;
 ;
;
 ;
;
 ;
;
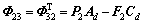 ;
;
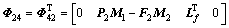 ;
;
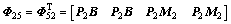 ;
;
 ;
;
 ;
;
 ;
; ;
;
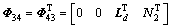 ;
;
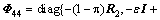
 ;
;
 ;
;
 ;
;



 ;
;
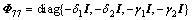 ;
;
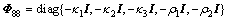 (21)
(21)
存在解正定矩阵P1,P2,R1,R2和S,矩阵F1,F2和Lf以及正常数σ,ε,λ,αi,βi,ηi,μi,δi,γi,ρi和kj (i=1, 2, j=1, 2, 3),则式(8)为最优保成本弹性滤波器,滤波器增益为 ,
,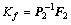 ,Lf,
,Lf,
 为滤波系统保成本上界。
为滤波系统保成本上界。
3 结论
针对一类状态系统和量测输出中同时含有非线性不确定项的时变时滞不确定参数系统,研究了鲁棒保成本弹性滤波器设计问题。系统中的非线性不确定项满足范数有界条件,系统参数不确定项满足广义匹配条件,弹性滤波器中的滤波增益不确定性满足加型增益变化条件。根据所研究的保成本性能目标,将弹性滤波器的设计问题归结为一个凸优化问题,以线性矩阵不等式组(LMIs)的形式给出,通过求解这个优化问题获得滤波器参数和保成本值的最小上界。
参考文献:
[1] Xie L, Soh Y C. Robust Kalman filtering for uncertain system[J]. Systems and Control Letters, 1994, 22(2): 123-130.
[2] Shaked U, de Souza C E. Robust minimum variance filtering[J]. IEEE Trans Signal Processing, 1995, 43(11): 2474-2483.
[3] Petersen I R, Mcfarlane D C. Optimal guaranteed cost control and filtering for uncertain linear systems[J]. IEEE Trans Automatic Control, 1994, 39: 1971-1977.
[4] Mahmoud M S. Robust linear resilient filtering of uncertain systems[J]. Automatica, 2004, 40: 1797-1802.
[5] Mahmoud M S. New filter design for linear time-delay systems[J]. Linear Algebra and its Applications, 2010, 434(4): 1080-1093.
[6] Yang G H, Guo X G. Insensitive H∞ filter design for continuous-time systems with respect to filter coefficient variations[J]. Automatica, 2010, 46(11): 1860-1869.
(编辑 杨幼平)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:浙江省科技计划项目(2009C33085); 温州市科技计划项目(S20100029)
通信作者:谢立(1974-),男,浙江杭州人,副教授,从事智能信息处理研究;电话:13606611192;E-mail: xiehan@zju.edu.cn